
MISUSE DETECTION
An Iterative Process vs. A Genetic Algorithm Approach
Pedro A. Diaz-Gomez and Dean F. Hougen
Robotics, Evolution, Adaptation, and Learning Laboratory (REAL Lab)
School of Computer Science, University of Oklahoma
Norman, OK, USA
Keywords:
Misuse detection, genetic algorithms, iterative process, false negative, false positive.
Abstract:
With the explosion of the Internet and its use, the development of security mechanims are quite important
in order to preserve the confidentiality, integrity, and availability of data stored in computers. However, the
growth of intrusions can make such mechanisms almost unusable, in the sense that the computation time
or space needed in order to mantain them can grow exponentially. This position paper presents an iterative
process for doing misuse detection, and compares it with another approach for doing that: a Genetic Algorithm.
1 INTRODUCTION
Every company or enterprise usually has a security
mechanism in order to protect data. One such security
mechanism is the Intrusion Detection System (IDS),
which monitors and detects intrusions, or abnormal
activities, in computers or computer networks. For
doing that, the IDS usually knows what constitutes
“normal” activity, and then a deviation of normality
could be an intrusion (Denning, 1986) or the IDS has
in advance patterns of suspicious activity that consti-
tute intrusions, and those are compared with current
activities, in order to determine if there is an intru-
sion. The former type of detection is called anomaly
detection and the later misuse detection.
There have been various mechanisms proposed for
doing intrusion detection. One of the most important
is the seminal work of Dorothy Denning, which pro-
poses a real-time statistical rule base system (Bace,
2000), which is an anomaly detector that builds the
rule base system based on user activity. Another
mechanism proposed is expert systems, where the
knowledge usually is entered as if-then-clauses (Bace,
2000) and that constitutes principally misuse detec-
tion. Other mechanisms include neural networks,
which could be anomaly detectors in the sense that
they are usually trained with “normal” activity and
then the neural network can find abnormal activity,
Genetic Algorithms (GAs), which evolve the possible
intrusions and could be misuse detectors, and so forth
(Bace, 2000).
Besides the possible drawbacks of almost any IDS
in storage and computation time used, is the problem
of false positives and false negatives. A false positive
is when the IDS sets an alarm indicating an intrusion
that, in reality, did not happen. A false negative is
when the IDS did not detect an intrusion or a devia-
tion from normality that constitutes an intrusion but
the intrusion really happened (Tjaden, 2004). Both
types of problems are critical. On one side, if the IDS
has many false positives, then the attention to a pos-
sible intrusion is diminished. On the other side, if the
IDS missed many possible intrusions, then it is almost
useless, and great damage can be caused to the system
it monitors if intrusions are not detected.
The iterative process used in this article is the re-
sult of our experience in working with GAs in doing
misuse detection in log files. It uses the concept of
a fitness function used in a GA for finding intrusions
(Diaz-Gomez and Hougen, 2006).
A GA has a fitness function that guides evolu-
tion, operators that try to simulate mating and selec-
tion of some natural systems, and parameters like the
crossover and mutation probabilities (Mitchell, 1998).
However, the fitness function used and the setting of
parameters is at the same time a difficulty, in the sense
that a “good” choice of those can give approximate
“good” solutions, but an incorrect choice of those can
455
A. Diaz-Gomez P. and F. Hougen D. (2007).
MISUSE DETECTION - An Iterative Process vs. A Genetic Algorithm Approach.
In Proceedings of the Ninth International Conference on Enter prise Information Systems - AIDSS, pages 455-458
DOI: 10.5220/0002410804550458
Copyright
c
SciTePress
give “bad” solutions, i.e., the algorithm could give
a high rate of false positives and/or negatives (Diaz-
Gomez and Hougen, 2005c). Heuristic tools, like a
GA, have been considered for doing misuse detec-
tion, because the problem is NP-Complete (M
´
e, 1998)
and/or because the search space is huge, in which case
an exhaustive search of possible intrusions would be
almost impossible in an affordable computation time.
2 MISUSE DETECTION
Usually an IDS processes log records received from
the operating system for a specific period of time in
order to have a complete set of user activity (Bace,
2000; Crosbie and Spafford, 1995). After that, the
IDS performs analysis of the current activity, using a
rule base system, statistics, or a corresponding heuris-
tic, in order to determine the possible occurrence of
abnormality or intrusion.
For the present, the misuse mechanism uses a pre-
defined matrix of intrusion patterns (M
´
e, 1998), so the
system knows in advance the appearance of misuse
and/or abuse. The bigger this table, the more space
and computation time is spent in the analysis. Previ-
ous work with a GA used a table of size 28x48 (Diaz-
Gomez and Hougen, 2006), where 28 was the num-
ber of activities to be considered—an activity could
be a user logging, reading of a specific file, execut-
ing a program, and so forth—and 48 was the number
of intrusion patterns. Present work uses hundreds and
more than one thousand intrusions, validates previous
work, and suggests an iterative system as another al-
ternative.
An intrusion can be specified by an array of activ-
ities to check, where each entry specifies the number
of activities of a specific type that should occur in or-
der to have an intrusion. Likewise, the results of the
user records gathered can be seen as an array, where
each entry specifies the total number of activities of
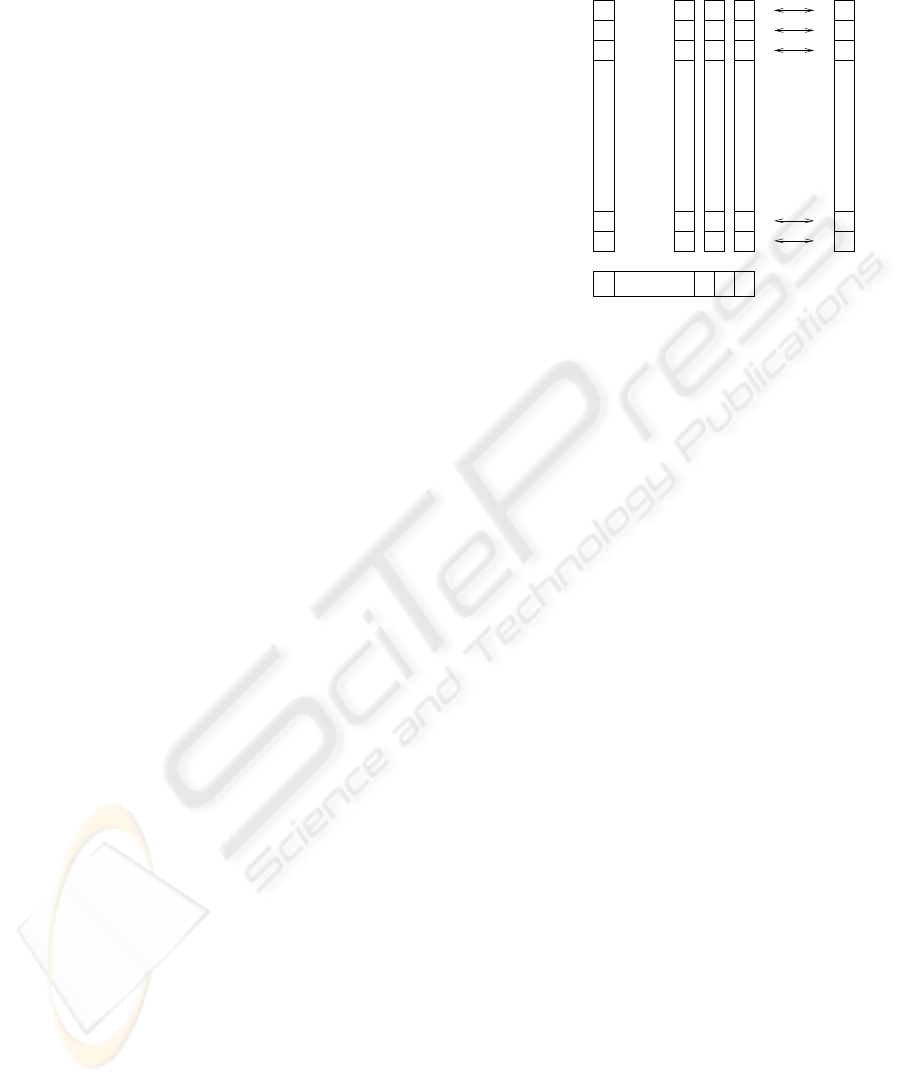
that specific type performed by a user. Figure 1 shows
an example of arrays P of intrusion patterns and an ar-
ray UA of user activity.
If an intrusion array pattern P is such that each en-
try of it is less or equal than each entry of the user’s
activity UA, then, it is possible that intrusion P has oc-
curred. However, looking at some possible intrusions
together, it is possible that one or several can occur,
but not all together, because adding each correspond-
ing entry, some results could be greater than the cor-
responding entry of the user activity vector UA (M
´
e,
1993; Diaz-Gomez and Hougen, 2006; Diaz-Gomez
and Hougen, 2005c). This is called a violation of the
constraint.
. . .
. . .
. . .
.
.
.
.
.
.
. .
. .
. .
.
.
.
. . .
. . .
. . .
.
.
.
. .
0
3
0
0
0
3
3
3
3
00
UA
P
Known Intrusions
OZ
Log in fails
Passwd file read
Port B open
File C printed
A execution
1
3
Hypothesis Array
31
10
Activity Type User Activity
0 1 0 1
Figure 1: Arrays of intrusions P, array of user activity UA,
and hypothesis array OZ.
2.1 Iterative Misuse Detection
The iterative process first checks each intrusion pat-
tern P to determine if it may have occurred. For do-
ing that, each entry of each P array is compared with
the corresponding UA entry. If there is no violation
of the constraint, i.e., if I
j
≤ UA
j
∀ 1 ≤ j ≤ M, where
M is the number of activities monitored, then P is a
possible intrusion. After finding all the possible intru-
sions, the iterative process begins to build two sets. It
adds iteratively the corresponding entries of the possi-
ble intrusions found, in order to check for a violation
of the constraint when considered together. If in do-
ing such addition, an entry of an intrusion violates the
constraint, then that possible intrusion is marked as
an exclusive intrusion. So, the result is going to be a
set of possible intrusions that can occur together and
a set of exclusive intrusions.
2.2 Genetic Misuse Detection
The genetic algorithm approach checks all possible
intrusions together, using an hypothesis array of ones
and zeros OZ, where a one in an entry means that that
type of intrusion may have occurred—see Figure 1.
Previous work uses an operator called the union op-
erator (Diaz-Gomez and Hougen, 2006). With the
union operator, the GA stores possible intrusions—if
any—and checks for violation of the constraint. The
result then—as the iterative process shows—is two
sets of possible intrusions, ones that can occur to-
gether (i.e., with no violation of the constraint) and
the others that in conjunction with the previous ones
ICEIS 2007 - International Conference on Enterprise Information Systems
456
Iterative
1,000
100
40
48 144 528 1008
0
10
20
30
40
50
60
70
80
90
100
110
Number of Arrays
Ave. Number of Possible Intrusions
1,000
100
40
Iterative
I
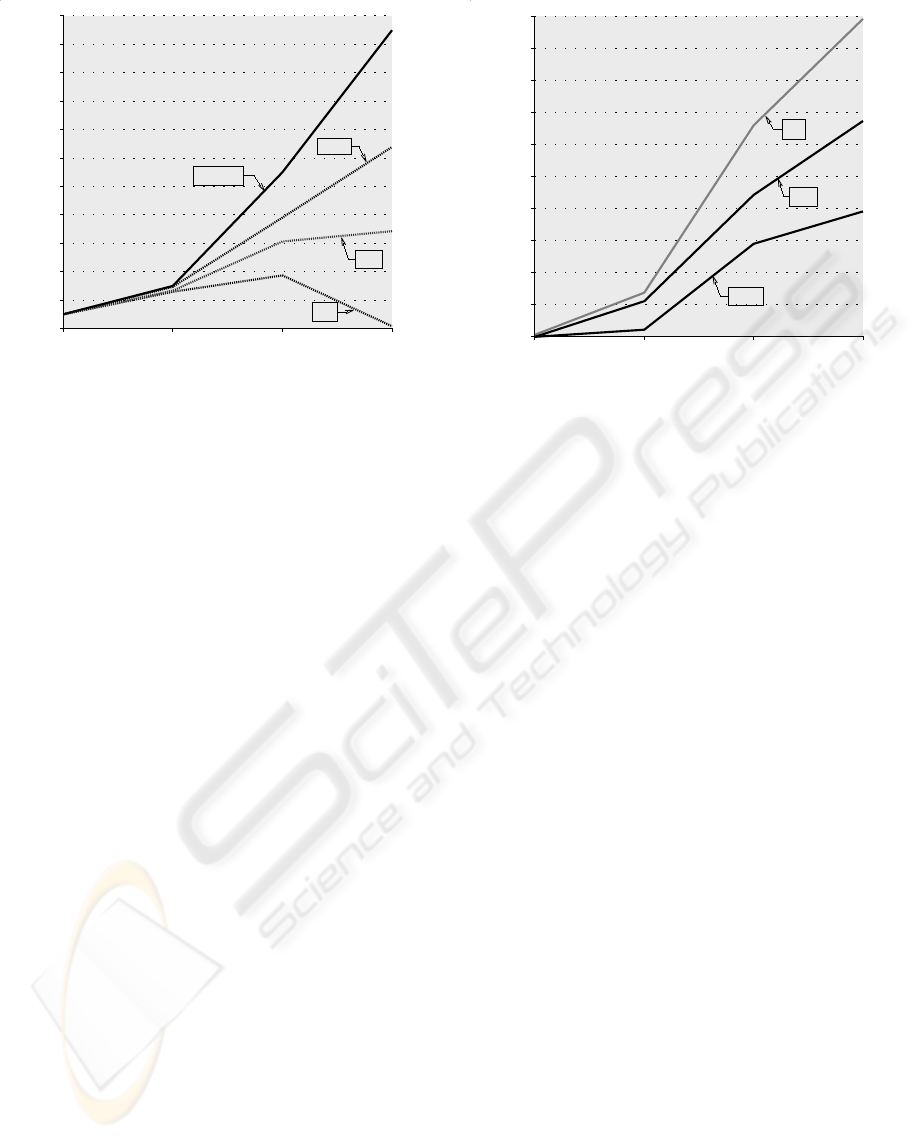
Figure 2: Average number of possible intrusions found by
a GA and total found by an iterative process. 40, 100 and
1, 000 individuals in the initial population. 30 runs on each
population size.
violate the constraint—if that is the case.
The GAs’ parameters used in these tests are the
following: 60% probability of one-point crossover,
2.4% probability of mutation per chromosome,
20, 000 generations, selection pressure of 1.5 (tour-
nament selection of size 2 with 75% of choosing the
fittest), and a population size of 40. With this configu-
ration of parameters the tests were perfomed 30 times
for 48, 144, 528, and 1008 intrusions.
3 ITERATIVE VS. GENETIC
APPROACH
Figure 2 shows the average number of possible intru-
sions found by the GA and the total number of intru-
sions found by the iterative process. There were no
false positives given by either algorithm and the iter-
ative process had no false negatives in these tests.
If the number of individuals in the GA’s popula-
tion is changed from 40 to 100 and 1, 000 (keeping
other parameters the same) the GA’s false negative
percentage is better, as expected (see Figure 3 for the
average number of false negatives when using 40, 100
and 1, 000 individuals). However, setting parameters
so that the quality of the solution is better is one of the
difficulties in working with GAs.
48 144 528 1008
0
10
20
30
40
50
60
70
80
90
100
Number of Arrays
False Negative Percentage
40
100
1,000
I
Figure 3: Average percentage of false negatives using a GA
with 40, 100, and 1, 000 individuals in the initial population.
30 runs on each population size.
3.1 Exclusive Intrusions
As stated in Section 2, the result of both algorithms
is two sets: one of possible intrusions (Y ) and the
other of possible intrusions that could not happen at
the same time as the previous ones because of vi-
olations of the constraint (M
´
e, 1993; Diaz-Gomez
and Hougen, 2006; Diaz-Gomez and Hougen, 2005c).
This is called exclusive set (X) (Diaz-Gomez and
Hougen, 2005c). For the case of the iterative process,
these two sets (Y and X) are always the same, but for
the GA case, the two sets could be different because
of the randomness involved in the process.
In this work, the exclusive set X was disaggre-
gated, i.e., the algorithm continues looking for con-
straints until a set of disjoint sets X
1
, X
2
, ..., X
h
is
found, the union of which is the set X, so the entire set
of possible intrusions is Y ∪ X
1
∪ X
2
∪ ... ∪ X
h
, where
Y ∩ X
1
∩ X
2
∩ ... ∩ X
h
=
/
0.
It should be emphasized that exclusive intrusions
makes this an NP-Complete problem because the so-
lution set Y ∪ X
1
∪X
2
∪...∪ X
h
is not unique. However,
the algorithms presented in this paper are finding one
solution, not all possible solutions.
3.2 Computational Complexity
The iterative process performs, for each P array, M
comparisons (M is the number of types of user ac-
tivity), and as there are N such arrays, then it spends
M ∗ N computation time. For the second step of look-
ing at the exclusive intrusions, that depends on the ac-
MISUSE DETECTION - An Iterative Process vs. A Genetic Algorithm Approach
457

tual number of possible intrusions found K. For each
type of activity M, it checks the common type of ac-
tivity in order to check for violations of constraints.
So for this case it spends M ∗ K computation time,
where K < N. In conclusion, the iterative process is
O(MN).
For the case of the GA, it depends on the popula-
tion size S, number of generations G and length M of
each P array. So, for each hypothesized array OZ—of
length N, and the ones that belong to the population—
the algorithm performs N calculations for each type of
activity, and as there are M types of activity, this gives
M ∗ N calculations. As the population size is S, for
each generation the algorithm performs M ∗ N ∗ P cal-
culations. As the algorithm has G generations, it gives
a total computational complexity of order O(MNSG).
Clearly, the GA cost is higher by O(PG) with the
down side of a false negative ratio that depends in part
on the population size (see Fig 3).
The computational complexity done by both algo-
rithms in finding the disjointed sets of possible intru-
sions is O(K
2
M), where K is the cardinality of the
disjointed set X (see section 3.1).
The space complexity is such that both algorithms
have to store the matrix of known intrusions and the
user activity (see Figure 1). The GA, additionally, has
to store the population that is of order O(SN).
4 CONCLUSIONS AND FUTURE
WORK
In this position paper we continue our previous work
(Diaz-Gomez and Hougen, 2005a; Diaz-Gomez and
Hougen, 2006; Diaz-Gomez and Hougen, 2005c;
Diaz-Gomez and Hougen, 2005b) using a GA for
doing misuse detection in log files, expanding the
number of intrusion arrays from 48 to 1, 008. Be-
sides that, the performance of an iterative process was
compared with a current implementation of a GA,
looking at the false negative ratio and computational
complexity of both algorithms. The iterative process
outperformed the GA for the test set, as established
by the false negative ratio and in computational and
space complexity. The population size of the GA
was increased in order to improve the quality of the
solution—fewer false negatives—but other parame-
ters may be changed in the GA as well, such as the
number of generations and the probability of the op-
erators, in trying to improve its performance. How-
ever, some of those possible changes may or may not
improve the quality of the solution and some may ex-
pend more computation time. The correct setting of
parameters is one of the difficulties in working with
GAs. Other heuristic methods, like neural networks,
can be addressed in order to continue comparing the
iterative process and the GA examined in this paper.
REFERENCES
Bace, R. G. (2000). Intrusion Detection. MacMillan Tech-
nical Publishing, USA.
Crosbie, M. and Spafford, G. (1995). Applying genetic pro-
gramming to intrusion detection. In Proceedings of
the AAAI Fall Symposium, pages 1–8.
Denning, D. E. (1986). An intrusion-detection model. In
Proceedings of the IEEE Symposium on Security and
Privacy, pages 118–131.
Diaz-Gomez, P. A. and Hougen, D. F. (2005a). Analysis and
mathematical justification of a fitness function used in
an intrusion detection system. In Proceedings of the
Genetic and Evolutionary Computation Conference,
pages 1591–1592.
Diaz-Gomez, P. A. and Hougen, D. F. (2005b). Analysis
of an off-line intrusion detection system: A case study
in multi-objective genetic algorithms. In Proceedings
of the Florida Artificial Intelligence Research Society
Conference, pages 822–823.
Diaz-Gomez, P. A. and Hougen, D. F. (2005c). Improved
off-line intrusion detection using a genetic algorithm.
In Proceedings of the 7th International Conference on
Enterprise Information Systems, pages 66–73.
Diaz-Gomez, P. A. and Hougen, D. F. (2006). A genetic al-
gorithm approach for doing misuse detection in audit
trail files. In Proceedings of the CIC-2006 Interna-
tional Conference on Computing, pages 329–335.
M
´
e, L. (1993). Security audit trail analysis using genetic
algorithms. In Proceedings of the 12th. International
Conference on Computer Safety, Reliability, and Se-
curity, pages 329–340.
M
´
e, L. (1998). GASSATA, a genetic algorithm as an alter-
native tool for security audit trail analysis. In Proceed-
ings of the First International Workshop on the Recent
Advances in Intrusion Detection.
Mitchell, M. (1998). An Introduction to Genetic Algo-
rithms. MIT Press.
Tjaden, B. C. (2004). Fundamentals of Secure Computer
Systems. Franklin and Beedle & Associates.
ICEIS 2007 - International Conference on Enterprise Information Systems
458
