GENERALIZED MULTICRITERIA OPTIMIZATION

SOFTWARE SYSTEM MKO-2

Mariana Vassileva, Vassil Vassilev, Boris Staykov

Department of Decision Support Systems, Institute of Information Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev Str.,bl. 29A, Sofia, Bulgaria

Danail Dochev

Department of Artificial Intelligence, Institute of Information Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev Str.,bl. 29A, Sofia, Bulgaria

Keywords: Decision Support Systems, Knowledge-based Systems, Multicriteria Decision Making, Multicriteria

Optimization, Interactive Methods, Classification-based Scalarizing Problems.

Abstract: The paper describes a generalized multicriteria decision support system, called MKO-2, which is designed

to model and solve linear and linear integer multicriteria optimization problems. The system implements the

innovative generalized classification-based interactive algorithm for multicriteria optimization with variable

scalarizations and parameterizations, which is applicable for different types of multicriteria optimization

problems (i.e., linear, nonlinear, mixed variables) as well as for different ways of defining preferences by

the decision maker. It can apply different scalarizing problems and strategies in the search for new Pareto

optimal solutions. The class of the problems solved, the structure, the functions and the user interface of the

MKO-2 system are described in the paper. The graphical user interface of MKO-2 system enables decision

makers with different degrees of qualification concerning methods and software tools to operate easily with

the system. It can be used both for education and for solving real-life problems. Because of its nature,

MKO-2 system applies specific expert knowledge of the field of multicriteria optimization and knowledge-

based (expert) subsystems, explicitly representing specific domain knowledge, as well as specific MO

solving knowledge, can be included in it concerning different levels of expertise.

1 INTRODUCTION

Different problems of planning, control, analysis and

monitoring in economy, transport, industrial

production, education, ecology and other spheres

may be reduced to decision making problems at

many criteria. These problems can be divided in two

separate classes depending on their formal statement

(Miettinen, 1999). One of these classes consists of

the problems of multicriteria optimization (MO), in

which a finite number of explicitly set constraints (in

the form of set of functions) define an infinite

number of feasible alternatives. These problems are

also called continuous multicriteria decision making

problems. Several criteria (or objective functions)

are simultaneously optimized in the feasible set of

solutions (or alternatives) in MO problems. In the

general case, there is no single solution that

optimizes all the criteria. Instead, there is a set of

solutions where improvement in the value of one

criterion leads to deterioration in the value of at least

another criterion. This set is known as a Pareto

optimal set. Any element of this set could be the

final solution of the MO problem. In order to select

the final solution, additional information is

necessary and it is supplied by the so-called decision

maker (DM). The information that the DM gives

reflects his/her global preferences with respect to the

quality of the solution obtained. Generally, MO has

to combine two aspects: optimization and decision

support.

One of the main approaches in solving MO

problems is the scalarizing approach. The major

representatives of this approach are the interactive

algorithms (Miettinen, 1999). Scalarization means

transformation of the MO problem into one or

283

Vassileva M., Vassilev V., Staykov B. and Dochev D. (2007).

GENERALIZED MULTICRITERIA OPTIMIZATION SOFTWARE SYSTEM MKO-2.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 283-288

DOI: 10.5220/0002388402830288

 SciTePress

several single-criterion optimization problems,

called scalarizing problems (SPs) with the following

main property: each optimal solution generated is a

Pareto or weakly Pareto optimal solution of the

original MO problem. The SPs are the basis, on

which different interactive MO methods are

developed. They define the type of information,

which the DM has to set, and also the type and

number of the Pareto optimal obtained as well as the

type of the MO problem (linear, non-linear, mixed

variables, etc.) that can be solved.

Up to now, a large variety of SPs have been

suggested and a number of interactive algorithms

have been developed based on them. The different

algorithms give different kind of information to the

DM and provide different possibilities for the DM to

control and stop the solution process.

The interactive MO algorithms use different SPs

(Miettinen, 1999, Vassileva et al., 2005) like the

Weighted SP (Gass and Saaty, 1955), the SP of ε –

Constraint Method (Haimes et al., 1971), the SP

STEM (Benayoun еt al., 1971), the Chebyshev SP

(Steur and Choo, 1983), the SP STOM (Nakayama

and Sawaragi, 1984), the SP of the Reference Point

(Wierzbicki, 1980), the SP GUESS (Buchanan,

1997), the SP of the Modified Reference Point

(Vassilev et al., 2001), the SP of the External

Reference Direction (Korhonen, 1997), the SP of the

Reference Direction (Vassilev and Narula, 1993),

the SP of the Internal Reference Direction (Narula et

al., 1994), the Classification-based SP NIMBUS

(Miettinen, 1999, Miettinen and Makela, 2006), the

Classification-based SP DALDI (Vassileva, 2000).

In the Weighted SP the DM defines his/her

preferences by the values of the criteria weights,

while in the SP of ε-constraint Method – by the

selection of one function for optimization and

defining the lower or upper bounds of change of the

remaining criteria. In the SP of the Reference Point

the so called reference point is determined by the

aspiration levels of the criteria and these levels are

the ones that the DM wishes or agrees to be obtained

in the new solution. Actually, these aspiration levels

of the criteria are parameters in all of the SPs of the

reference point. In all of the classification-based SPs

not only the aspiration levels could be parameters of

the problem, but also the directions and intervals of

alteration in the criteria values that the DM wishes

or agrees to be obtained in the new Pareto optimal

solution. Such parameters of a classification-based

SP could also be the values of the criteria in the

currently obtained solution. By setting desired or

acceptable alterations in the values of the criteria in

the currently obtained solution in the classification-

based SPs, the DM indirectly classifies the separate

criteria in different groups.

Among the well-known decision support systems

(DSSs), which support the solving of MO problems,

are the following systems: VIG, NIMBUS, DIDAS,

CAMOS, LBS, DINAS, ADBASE, MOLP-16,

MONP-16 and MOIP (Miettinen, 1999, Vassilev et

al., 1997, Wiestroffer and Narula, 1997). Each

multicriteria DSS contains control modules,

interface modules and optimization modules. The

optimization modules realize different multicriteria

and single-criterion algorithms. In most of the MO

DSSs developed up to now, basic attention is paid to

the MO interactive algorithms. Two types of MO

interactive algorithms are included in the well-

known MO DSSs. The first type comprises

interactive algorithms of the reference point and the

reference direction (as in the systems DIDAS, VIG,

CAMOS, DINAS and LBS). The second type

includes classification-based algorithms (as in

NIMBUS, MOLP-16, MONP-16 and MOIP).

The new programming languages and operating

systems make possible the considerable

improvement of the control modules and interface

modules of MO DSSs. The description of DM’s

local preferences and the generating of new

solutions for evaluation however depend to a higher

degree on the type of the MO and single-criterion

optimization algorithms included in the system. As

shown in (Miettinen, 1999), the major part of the

MO DSSs, developed up to now, include MO

methods of the reference point and the reference

direction, and they are intended to solve continuous

MO problems. This has significantly influenced the

design of these systems with respect to the input data

entry, the interactive solution of MO problems and

the visualization of the current and final results.

The paper describes the basic elements of the

developed generalized MO DSS, called MKO-2,

which supports the solving of linear and linear

integer MO problems. The proposed generalized

classification-based interactive algorithm, called

GENWS-IM, which is the basis of the system, uses

the scalarizing approach for solving MO problems

and allows the DM to define not only the aspiration

levels at each iteration, as it is in most of the

classification-based MO interactive algorithms

known up to now, but also to set aspiration intervals

and aspiration directions of change in the values of

some or of all the criteria. Such kind of generalized

MO DSS that implements generalized MO

interactive methods, based on the scalarizing

approach, is an innovative one in the field of MO. In

distinction with the traditional one-method MO

ICEIS 2007 - International Conference on Enterprise Information Systems

284

DSSs, the MKO-2 system can be used successfully

both for education and for solution of real-life

problems, not only with the help of one particular

MO method but combining different MO methods.

In this way, the MKO-2 DSS can be used not only

for direct solving of MO problems but also for

comparing and analyzing different solutions of given

MO problem using different preference information,

set by the DM, and different MO interactive

methods. Thereby, this generalized MO DSS enables

the DM to be more confident of the solving process

and more satisfied by the final solution of the MO

problem being solved. Because of its nature, such

kind of MO DSS applies specific expert knowledge

of the MO field and, therefore, knowledge-based

(expert) subsystems, explicitly representing specific

domain knowledge, as well as specific MO solving

knowledge, can be included in it concerning

different levels of expertise (i.e., recommendations

like what kind of preference information and

interactive methods to be used by the DM for

solving the corresponding classes of MO problems).

The rest of the paper is organized as follows.

The second section describes the proposed

generalizing classification-based scalarization

problem, called GENWS. The generalized

classification-based interactive algorithm GENWS-

IM is described in the third section and the MO DSS

MKO-2 is stated in the fourth section. Finally, the

conclusions are given in the last section.

2 GENERALIZED SCALARIZING

PROBLEM GENWS

The general MO problem of can be stated as

follows:

maximize {

()

, k∈K }

subject to x

∈X,

where

f (x):

→

R, k

∈

K={1, 2,…,p} are

different criteria (or objective functions) which have

to be simultaneously maximized.

The solution x

∈X is a Pareto optimal solution of

the MO problem if there does not exist another

solution

Xx ∈ , for which is valid

()

(

)

xfxf

≥ ,

for every k

∈K and

() ()

xfxf

> for at least one

index k

∈K. Furthermore, the solution x

∈

X is a

weakly Pareto optimal solution of the MO problem

if there does not exist another

Xx ∈ , for which is

valid

(

)

(

)

xfxf

> , for every k∈K. The vector

(

)

(

)

(

)

Zxfxfxfz

∈== ,...,)(

is a (weakly)

Pareto optimal solution in the criteria space if x

∈

is a (weakly) Pareto optimal solution in the decision

space. A reference point (Wierzbicki, 1980) or a

reference vector is a vector that consists of desirable

or aspiration values set by the DM for each criterion.

These aspiration values may be achievable or not.

An important concept in many interactive

methods is classification of criteria into classes,

where the DM studies the criteria values at the

current solution and expresses hopes of what kind of

values he/she wishes to obtain (Miettinen, 1999,

Narula and Vassilev, 1994). An example of

classification can be given as follows as assigning

the criteria into the following classes:

≥

, a set of

criteria, the current values of which the DM wishes

to improve up to a given or desired levels;

, a set

of criteria, the current values of which the DM

wishes to improve;

≤

, a set of criteria, the current

values of which the DM agrees to be deteriorated till

given acceptable levels;

, a set of criteria, the

current values of which the DM agrees to be

deteriorated;

, a set of criteria, the current values

of which the DM does not wish to be deteriorated;

, a set of criteria, the values of which the DM

allows to vary within a given interval;

, a set of

criteria, for which the DM has no explicit

preferences about the criteria values alteration.

Now we can formulate the generalized SP

GENWS (Vassileva et al., 2005) where the starting

point for the classification is assumed to be the

current (weakly) Pareto optimal solution and the

problem is of the form

minimize

)(xS

(1)

⎡

⎤

∑

⎢

⎥

⎣

⎦

- f (x) G

ÎK

subject to

{

⎡⎤ ⎡⎤

⎣⎦ ⎣⎦

³£

11 2 2

kk1 kk k2

kÎK kÎK

ax F -f(x) G R max F -f(x) G R

}

⎡⎤ ⎡⎤

⎣⎦ ⎣⎦

3344

kk k3 kk k

kÎK kÎK

ax F -f(x) G R max F -f(x) G +

GENERALIZED MULTICRITERIA OPTIMIZATION SOFTWARE SYSTEM MKO-2

285

c>=

f(x)³z ,kÎ K ÈK , (2)

kk k

C ³f(x)³E ,k Î K ,

(3)

c£

kkk

f(x)³z -D ,kÎ K , (4)

c- c+ ><

kkk kk

z-t£f(x)£z+t,kÎK , (5)

∈X, (6)

where:

12345

kkkkk

G,G,G,G,G are scaling,

normalizing or weighting coefficients;

kkk

EDC ,,

are parameters (

kkk

CzED ≤≤> ;0 );

54321

,,,,

kkkkk

FFFFF are parameters, connected

with aspiration, current and other levels of the

criteria values;

321

,, RRR are equal to the arithmetic

operation “+” or to the separator “ , ” ;

−

t and

are the upper and lower limit of the acceptable for

the DM interval of alteration of the criterion with an

index

∈ Kk (

−

t >0;

t >0);

z is the value of

the k-th criterion with an index in the current

preferred solution.

It is proved in (Vassileva et al., 2005) that the

solutions obtained by solving the generalized SP

GENWS are always (weakly) Pareto optimal.

Altering some parameters of the generalized SP

GENWS (Vassileva et al., 2005), the following

thirteen, known in the literature, SPs, which were

introduced in Section 1, can be obtained: the

Weighted SP, SP of ε–constraint Method,

Chebyshev SP, SP STEM, SP STOM, SP of the

Reference Point, SP GUESS, SP of the Modified

Reference Point, SP of the External Reference

Direction, SP of the Reference Direction, SP of the

Internal Reference Direction, Classification-based

SP NIMBUS, and Classification-based SP DALDI.

3 GENERALIZED INTERACTIVE

METHOD GENWS-IM

On the basis of the generalized classification-based

SP GENWS, a generalized classification-based

interactive algorithm for solving MO problems with

variable scalarizations and parameterizations, called

GENWS-IM, is designed, having the following

characteristics:

• the DM may set his/her preferences with the

help of the criteria weights, ε – constraints,

desired and acceptable levels of change of the

criteria values, desired and acceptable levels,

directions and intervals of alteration in the

criteria values, etc.;

• during the process of the MO problems solving,

the DM may change the way of presenting

his/her preferences;

• starting from one and the same current Pareto

optimal solution and applying different SPs, the

DM may obtain different new Pareto optimal

solutions at given iteration, and this opportunity

is especially useful in education and in

comparison of different SPs.

The most wide-spread interactive algorithms for

solving MO problems are the algorithms of the

reference point, the algorithms of the reference

direction and the classification-based algorithms.

GENWS-IM interactive algorithm is an algorithm

with variable scalarizations and parameterizations

and it is a generalization of a large number of the

above mentioned algorithms. This generalization is

with regard to the classes of the problems solved, the

type of defined preferences, the number and type of

the scalarizing problems used, as well as the

strategies utilized in the search for new Pareto

optimal solutions.

4 GENERALIZED

MULTICIRETIRA

OPTIMIZATION SOFTWARE

SYSTEM MKO-2

The MO DSS MKO-2, developed on the GENWS-

IM, has a graphical interface in relation both to the

classes of the MO problems being solved and to the

possibilities for setting the DM’s preferences.

MO DSS MKO-2 operates under the control of

MS Windows operating system. This software

system is designed to aid the solution of linear and

linear integer MO problems. It may be used both for

education and for solving real-life problems. MKO-2

system can also be extended to solve non-linear MO

problems. For this purpose, some algorithms,

solving non-linear continuous single-objective

problems have to be included and new interface

modules have to be added as well, connected with

the solution of non-linear MO problems.

MO DSS MKO-2 consists of three main groups

of modules – a control program, optimization

modules and interface modules. The control program

is integrated software environment for creation,

processing and storing of files associated with

ICEIS 2007 - International Conference on Enterprise Information Systems

286

MKO-2, as well as for linking and execution of

different types of software modules. The

optimization modules realize the generalized

interactive algorithm GENWS–IM for solving MO

problems, two simplex algorithms for solving

continuous single-criterion problems (Vanderbei,

1996), an algorithm of “Branches and Bounds” type

for exact solution of linear integer single-criterion

problems (Wolsey, 1998) and an algorithm for

approximate solution of linear integer single-

criterion problems (Vassilev and Genova, 1991).

The interface modules provide the dialogue between

the DM and the system during the entry and

correction of the input data of the MO problems

being solved, as well as during the interactive

process of their solution. These modules enable the

dynamic numerical and graphical visualization of

the solving process parameters.

One of the main functions of MKO-2 system is

to enable the extension of DM’s possibilities to set

his/her preferences in the terms of the criteria

weights, ε – constraints, desired and acceptable

levels of alteration in the criteria values, desired and

acceptable directions of change of the criteria

values, desired and acceptable levels, as well as

directions and intervals of alteration of the criteria

values. Thirteen SPs are generated in MKO-2 DSS

in order to realize these possibilities. Depending on

DM’s preferences, these SPs are automatically

generated by the generalized SP GENWS by

changing its structure and parameters.

MO DSS MKO-2 system presents to the DM

different windows intended for entry and correction

of the MO problem’s criteria and constraints, as well

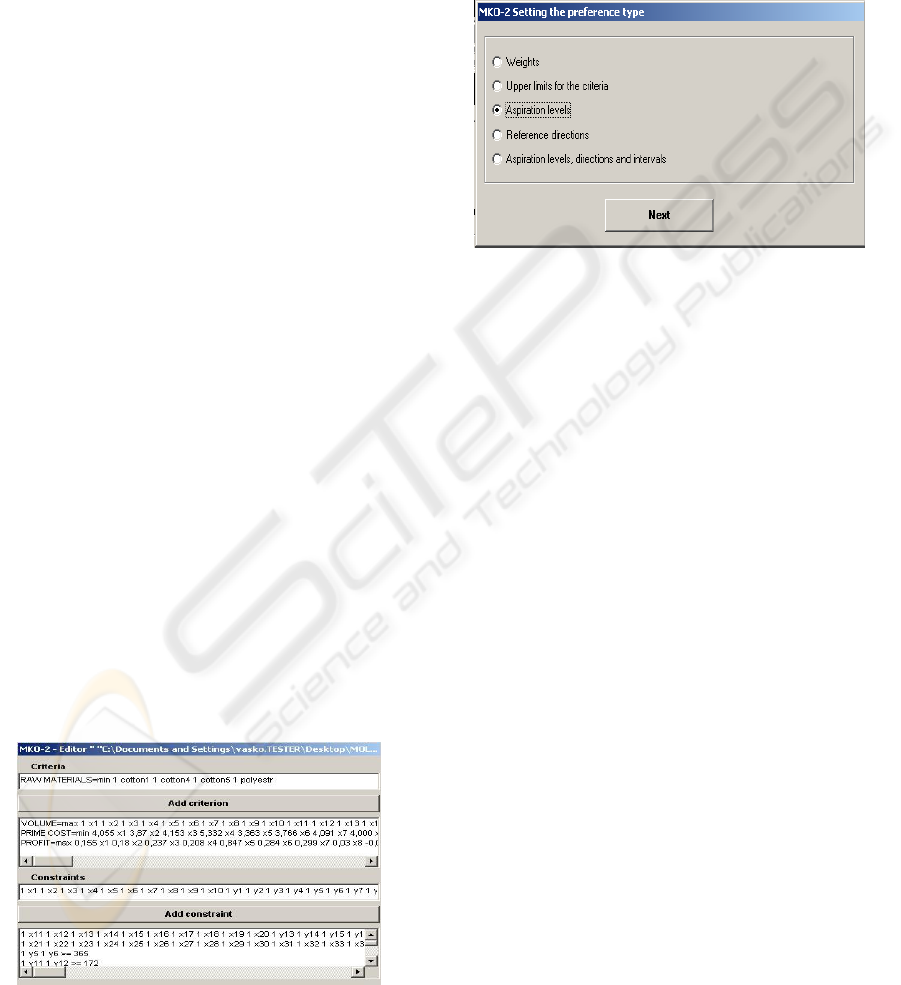
as for setting his/her preferences. The window,

presented in figure 1, is the basic window of the

editor for input data entry, called “MKO-2-Editor”.

It is used to set the data of a real-life MO linear

integer problem for operative planning of the

production program of a spinning department in a

Figure 1: MKO-2 – Editor Main Window.

textile enterprise (Vassileva, 2006).

The window, presented in figure 2, is designed

to identify the type of DM’s preferences. The DM

may select among five types of preferences and let

assume that he/she has selected to set the

preferences by aspiration levels (or reference point).

In order to enter the different types of DM’s

preferences, different windows are used.

Figure 2: Type of the DM’s Preferences.

5 CONCLUSIONS

The generalized MO DSS MKO-2 can be extended

to model and solve not only linear and linear integer

MO problems but also non-linear MO problems as

well as a web-based version of the system can be

developed.

The improved graphical user’s interface of

MKO-2 software system both to the classes of the

MO problems solved and to the possibilities for

setting DM’s preferences, facilitates the operation of

decision making persons of different qualification

level relating to the optimization algorithms and

software tools used. MKO-2 system is an innovative

kind of DSS that implements generalized MO

interactive method and can be used successfully both

for education and for solution of real-life problems,

not only with the help of one particular MO method

but combining different MO methods. In addition to

direct solving of MO problems the MKO-2 DSS can

be used also for comparing and analyzing different

solutions of given MO problem. Due to the fact that

such kind of generalized MO DSS applies specific

knowledge of the MO field, the future plans

concerning the enhancement of the MKO-2 DSS

comprise including of knowledge-based (expert)

subsystems, explicitly representing specific domain

knowledge, as well as specific MO solving

knowledge. The aim of these subsystems is to

analyze the information, supplied by the DM about

different MO problems, as well as to provide this

GENERALIZED MULTICRITERIA OPTIMIZATION SOFTWARE SYSTEM MKO-2

287

analysis and to recommend a course of DM’s action.

They will include, e.g., recommendations as what

kind of preference information and interactive

methods to be used for solving the corresponding

classes of MO problems.

ACKNOWLEDGEMENTS

This paper is a part of the following projects at the

Institute of Information Technologies - Bulgarian

Academy of Sciences: FP6 INCO-CT-2003/0003401

HABUSKA “Networking Centres of High Quality

Research on Knowledge Technologies and

Applications” and “Interactive Algoritms and

Software Systems Supporting Multicriteria Decision

Making” (NSF of Bulgarian Ministry of Education

and Science under the contract № I-1401\2004).

REFERENCES

Buchanan, J.T., 1997. A Naive Approach for Solving

MCDM Problems: The GUESS Method. In Journal of

the Operational Research Society, Vol. 48, pp. 202-

206.

Benayoun, R., Montgolfier, J., Tergny, J, Laritchev, O.,

1971. Linear Programming with Multiple Objectives

Functions: Step Method (STEM). In Mathematical

Programming, Vol. 1, pp. 136-375.

Gass, S., Saaty T., 1955. The Computational Algorithm

for the Parametric Objective Function. In Naval Research

Logistics Quarterly, Vol. 2, pp. 39-45.

Haimes, Y., Lasdon, L., Wismer, D., 1971. On a

Bicriterion Formulation of the Problems of Integrated

System Identification and System Optimization. In

IEEE Transactions on Systems, Man, and Cybernetics,

Vol. 1, pp. 296–297.

Korhonen, P., 1997. Reference Direction Approach to

Multiple Objective Linear Programming: Historical

Overview. In Essay in Decision Making: A Volume in

Honour of Stanley Zionts, (M. Karwan, J. Spronk and

J. Wallenius, Eds.), pp. 74-92.

Miettinen, K., 1999. Nonlinear Multiobjective

Optimization, Kluwer Academic Publishers. Boston,

edition.

Miettinen, K., Makela, M., 2006. Synchronous Approach

in Interactive Multiobjective Optimization. In

European Journal of Operational Research, Vol. 170,

pp. 909-922.

Nakayama H., Sawaragi, Y., 1984. Satisficing Trade-Off

Method for Multiobjective Programming. In

Interactive Decision Analysis. Lecture Notes in

Economics and Mathematical Systems (M. Grauer and

A. Wierzbicki, Eds.), Vol. 229, pp. 113-122.

Narula, S. , Vassilev, V., 1994. An Interactive Algorithm

for Solving Multiple Objective Integer Linear

Programming Problems. In European Journal of

Operational Research, Vol. 79, pp. 443-450.

Narula, S., Kirilov, L., Vassilev, V., 1994. Reference

Direction Approach for Solving Multiple Objective

Nonlinear Problems. In IEEE Transactions on

Systems, Man and Cybernetics, Vol. 24, pp. 804-806.

Steuer, R., Choo, E., 1983. An Interactive Weighted

Tchebycheff Procedure for Multiple Objective

Programming. In Mathematical Programming, Vol.

26, N 3, pp. 326-344.

Vanderbei, R., 1996. Linear Programming: Foundations

and Extensions. Kluwer Academic Publishers.

Vassilev, V., Genova, K., 1991. An Algorithm of Integer

Feasible Directions for Linear Integer Programming.

In European Journal of Operational Research, Vol.

52, pp. 203-214.

Vassilev, V., Narula, S., 1993. A Reference Direction

Algorithm for Solving Multiple Objective Integer

Linear Programming Problems. In Journal of the

Operational Research Society, Vol. 44, N 12, pp.

1201-1209.

Vassilev, V., Narula, S., Vladimirov, V., Djambov, V.,

1997. MOIP: A DSS for Multiple Objective Integer

Programming Problems. In Multicriteria Analysis (J.

Climaco, Ed.), pp. 259-268.

Vassilev, V., Narula, S., Gouljashki, V., 2001. An

Interactive Reference Direction Algorithm for Solving

Multi-Objective Convex Nonlinear Integer

Programming Problems. In International Transactions

in Operational Research, Vol. 8, pp. 367-380.

Vassileva, M., 2000. Scalarizing Problems of

Multiobjective Linear Programming Problems. In

Problems of Engineering Cybernetics and Robotics,

Vol. 50, pp. 54-64.

Vassileva, M., Miettinen, K., Vassilev, V., 2005.

Generalized Scalarizing Problem GENWS. In Working

Papers of IIT-BAS, N IIT/WP-205.

Vassileva, M., 2006. Operative Planning of the Production

Program in a Textile Enterprise with the Help of

МКО-2 Software System. In Cybernetics and

Information Technologies, Vol. 6, N 1, pp. 58-68.

Wierzbicki, A. P., 1980. The Use of Reference Objectives

in Multiobjective Optimization. In

Multiple Criteria

Decision Making Theory and Applications. Lecture

Notes in Economics and Mathematical Systems, Vol.

177, pp. 468-486.

Wiestroffer, H., Narula, S., 1997. The State of Multiple

Criteria Decision Support Software. In Annals of

Operations Research, Vol. 72, pp. 299-313.

Wolsey, L. A., 1998. Integer Programming. Wiley-

Interscience.

ICEIS 2007 - International Conference on Enterprise Information Systems

288