USING FUZZY DATACUBES IN THE STUDY OF TRADING

STRATEGIES

M. Delgado Calvo-Flores, J. F. Nu

nez Negrillo

Department of Computer Science and Artiﬁcial Intelligent, University of Granada

E. Gibaja Galindo

Department of Informatics and Numeric Analysis, University of Cordoba

C. Molina Fern

andez

Department of Computer Science, University of Jaen

Keywords:

Fuzzy OLAP, imprecision, exploratory analysis.

Abstract:

A fuzzy multidimensional model can be used for exploratory analysis, modelling complex concepts that are

very difﬁcult to use in crisp ones. Some problems, as the edge problem, can be reduced using this approach.

To hide the complexity of the fuzzy logic in this situation is important. In this paper we present an application

of a fuzzy multidimensional model, that uses two layer representation to hide the complexity to the user, in

the study of trading strategies.

1 INTRODUCTION

OLAP systems are exploratory analysis tools that are

designed to work with a high amont of data in an ef-

ﬁciently way. Some statistical software include this

kind of tools (e.g. SPSS has an analysis functionality

based on a simple model of DataCubes).

Some concepts are not well modelled using crisp

models (e.g. near the average value, a young com-

pany, etc.). Fuzzy logic has been widely used to

model concepts in a more natural way to user. Us-

ing a fuzzy multidimensional model allows to apply

OLAP using fuzzy concepts and to get more intu-

itive results. Nowadays, the use of data from different

sources and the use of semi-structured (e.g. XML)

and non-structured (e.g. plain text) sources is normal.

Now the systems need to manage imprecision in the

data and more ﬂexible structures to represent the anal-

ysis domains. The fuzzy logic can help us to model

this kind of imprecision. Some times we need to cat-

egorize continues values to reduce the complexity of

the analysis. If we do it by dividing the range using

crisp intervals the result can present the edge problem:

two values very near belong to different intervals. If

we relax the edge of the intervals we can reduce this

Corresponding author. Phone: +34 953 212 883.

problem. These relaxed intervals can be modelled if

we use a fuzzy multidimensional model.

In this paper we propose to use a fuzzy multidi-

mensional model to analyze data from the behavior of

trading strategies and avoid the problems mentioned.

The paper is organized as follow: next section is ded-

icated to present the main concepts of the fuzzy mul-

tidimensional model used and the OLAP system that

implements it; section 3 presents the DataCube built

and (Section 4) some examples of analysis over it.

The main conclusions are collected in last section.

2 FUZZY MULTIDIMENSIONAL

MODEL

In this section we brieﬂy introduce the fuzzy multidi-

mensional model. A more detailed description can be

found in (Molina et al., 2006; Delgado et al., 2004).

Here we only present the main concepts needed to un-

derstand the model implemented.

2.1 Fuzzy Multidimensional Structure

Definition 1 A dimension is a tuple d = (l,≤

⊥

⊤

)

where l = l

,i = 1,...,n so that each l

is a set of values

164

Delgado Calvo-Flores M., F. Nuñez Negrillo J., Gibaja Galindo E. and Molina Fernández1 C. (2007).

USING FUZZY DATACUBES IN THE STUDY OF TRADING STRATEGIES.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 164-169

DOI: 10.5220/0002386001640169

 SciTePress

= {c

,...,c

} and l

∩l

0 if i6= j, and ≤

is a

partial order relation between the elements of l so that

≤

if ∀c

∈ l

⇒ ∃c

∈ l

⊆ c

. l

⊥

and l

⊤

are two elements of l so that ∀l

∈ l l

⊥

≤

⊤

We denote level to each element l

. To identify

the level l of the dimension d we will use d.l. The

two special levels l

⊥

and l

⊤

will be called base level

and top level respectively. The partial order relation

in a dimension is what gives the hierarchical relation

between levels.

Definition 2 For each pair of levels l

and l

such that

∈ H

, we have the relation µ

: l

× l

→ [0,1] and

we call this the kinship relation.

If we use only the values 0 and 1 and we only al-

low an element to be included with degree 1 by an

unique element of its parent levels, this relation rep-

resents a crisp hierarchy. If we relax these conditions

and we allow to use values in the interval [0,1] with-

out any other limitation, we have a fuzzy hierarchical

relation.

Definition 3 We say that any pair (h,α) is a fact

when h is an m-tuple on the attributes domain we want

to analyze, and α ∈ [0, 1].

The value α controls the inﬂuence of the fact in

the analysis. The imprecision of the data is managed

by assigning an α value representing this imprecision.

Now we can deﬁne the structure of a fuzzy DataCube.

Definition 4 A DataCube is a tuple C =

(D,l

,F,A,H) such that D = (d

,...,d

) is a set

of dimensions, l

= (l

,...,l

) is a set of levels

such that l

belongs to d

, F = R ∪

0 where R is

the set of facts and

0 is a special symbol, H is an

object of type history, A is an application defined as

A : l

× ... × l

→ F, giving the relation between the

dimensions and the facts deﬁned.

For a more detailed explication of the structure

and the operations over then, see (Molina et al., 2006;

Delgado et al., 2004).

2.2 User View

Over the structure presented, we deﬁned a new layer.

Its main objective is to hide the complexity of the

model and provide the user with a more understand-

able result. Using fuzzy summary operators, we de-

ﬁne the user view. As an example of this type of op-

erator, we can use the one proposed in (Blanco et al.,

2003). This operator proposes the use of the fuzzy

number that best ﬁts, in the sense of fuzziness, the

fuzzy set or fuzzy bag. We can use more simple oper-

ators as the weighted average.

Figure 1: Graphical way to represent fuzzy numbers.

To give an intuitive way to interpret the results is

important, as shown by Codd et al. in the 11th OLAP

product evaluation rule ((Codd, 1993)). We propose

two methods to represent fuzzy numbers in a graphi-

cal way as an user view. Both approaches are shown

in Figure 1. In Figure 1.a the approach followed is

to use a color gradient to represent the membership

grade of the values: a clearer color means a low mem-

bership degree, and an intense color means a high

membership. The other approach (Figure 1.b) con-

sists on changing the width of a bar to represent the

membership: a low membership degree is represented

by a thicker bar than the one for a high degree.

2.3 F-Cube Factory System

In this section we comment the main characteristics of

F-Cube Factory, the system that implements the fuzzy

model proposed, in addition to others models, see

(Delgado et al., 2005) for more details. The system is

built using server/client architecture. The server im-

plements the main functionality over the DataCubes

(deﬁnition, management, queries, aggregation opera-

tors, user views operators, API for DataCube access,

etc.). The client we have developed is web based and

is thought to be light enough to be used in a personal

computer and to give an intuitive access to server

functionality (hiding the complexity of using a DML

or DDL to the user).

The DataCube deﬁned in next section and the ex-

amples queries over it (Section 4) have been built us-

ing this system.

3 TRADING STRATEGIES

DATACUBE

In this section we present the structure of the Dat-

aCube built using the fuzzy multidimensional model

presented. The DataCube built is shown in Figure 2.

3.1 Dimensions

We have deﬁned 13 dimensions. In all of them we

have used the minimum and maximum operator as

USING FUZZY DATACUBES IN THE STUDY OF TRADING STRATEGIES

165

t-norm and t-conorm when calculating the extended

kinship relation. In next sections we present the struc-

ture of each one.

Strategy: We consider 107 different strategies

and we classify them according to two characteristics:

Style, been the possible values day, base and anti;

and Frequency, according to if the strategy considers

a short or medium period in its normal application.

Proﬁt: This annualized performance takes into

account commissions, slippages, and management

expenses. The values are in the interval [-50,70].

Over these values, we have deﬁned three categories

considering if the value is bad, normal or good. There

is no standard to deﬁne the edge between the labels,

and most of the times experts use imprecise expres-

sions to deﬁne then. So, we have used fuzzy con-

cepts in the dimension to manage the relationships be-

tween the concrete values and the quality. The fuzzy

intervals are represented in Figure 3. Under these

circumstances, the structure of the dimension built

is Proﬁt = ({Values, Quality,All},≤

Profit

,Values,All),

where ≤

Profit

is the relation that deﬁnes the hierarchi-

cal relations as follows: Values ≤

Profit

Values, Val-

ues ≤

Profit

Quality, Values ≤

Profit

All, Quality ≤

Profit

Quality, Quality ≤

Profit

All, All ≤

Profit

All.

Sharpe ratio: The sharpe ratio is a measure of

risk-adjusted performance of an investment asset, or

a trading strategy. This variable is used to character-

ize how well the return of an asset compensates the

investor for the risk taken. When two assets are com-

pared, the one with the highest sharpe ratio provides

a greater return for the same risk. Investors are often

advised to pick investments with high sharpe ratios.

This value is often used to rank the performance of

portfolio or mutual fund managers. On this variable,

the range of values is [-5,5].

We have deﬁned three categories to classify ac-

cording to the quality as in the previous dimension.

We have considered three labels depending on the val-

ues can be considered bad, normal or good to select

the trading strategy. As in other dimensions, the mem-

bership of each value to a category is not well deﬁned,

so we consider fuzzy intervals to build the kinship re-

lations of the values (Figure 7).

The structure of the dimension is analogous

to previous one: Sharpe Ratio = ({Values,

Quality,All},≤

,Values,All).

Loss series (Drawdown): This is the greatest loss

sequence, or rather, the greatest drop between the

peak of accumulated proﬁt and the lowest point. Mea-

surement begins when the fall starts and ends when a

new maximum is reached. The values of the examples

are in the range [0,100] and, as can be deduced from

the explanation, high values are the bad ones and the

low ones are translated into a good performance of the

strategy. The edges between good and normal, as well

as between bad and normal, are not deﬁned in a crisp

manner. If we consider them as crisp ones, two values

very near con be considered as belonging to differ-

ent categories. The fuzzy intervals used are shown in

Figure 4. Drawdown dimension is deﬁned as follows:

Drawdown = ({Values, Quality, All},≤

,Values,All).

Potential: This is a measure of the performance

in relation to the maximum loss series, and the val-

ues belong to the interval [-2,6]. The structure of

the dimension is as follows: Potential = ({Values,

Quality,All},≤

Potencial

,Values,All), where the kinship

relations between the values of the level Values and

Quality are represented in Figure 8.

Consistency: In our particular case, this variable

refers to the number of negative results over time. It

presents values in [-4,4]. The values below 0 and near

to this value are not good because it means a large

number of negative results. Values near the upper

edge represent a good performance of the strategy.

To characterize this behavior we deﬁne three cate-

gories: the bad values, the good ones and an interval

between both than represents a normal situation. Fig-

ure 5 presents the imprecise intervals proposed. The

structure of the dimension is Consistency = ({Values,

Quality,All},≤

Consistency

,Values,All).

Reliability: This variable represents the percent-

age of winning trades considering all the trades. As it

is a percentage, the values are in the interval [0,100],

being the greatest ones the good performance for a

strategy. If the value is under the 50%, the strategy

performs badly. The values in the middle are consid-

ered as normal situation (Figure 9). The structure of

the dimension is analogous to previous ones.

E01 and E04: These variables are the one-year

and four-year stars following the Standard & Poors’

method. By dividing the strategy’s average relative

performance by the volatility of its relative perfor-

mance, we are measuring not only its ability to out-

perform its peer but also to do so in a consistent way;

the higher the ratio, the greater the strategy’s ability

to outperform its peers consistently. The number of

stars depends on the relative position of the strategy

according to the others considered. If a a strategy has

1 or 2 stars, it is considered a bad one; if it presents 4

or 5, it is considered a good one, and in the case of 3

stars, the strategy presents a normal behavior. In this

case, the kinship relations between the values and its

quality is crisp.

The structure of the dimensions are as follows:

E01 = ({Values, Quality,All},≤

E01

,Values,All), and

E04 = ({Values, Quality,All},≤

E04

,Values,All).

Risk: The risk combines the probability of a nega-

ICEIS 2007 - International Conference on Enterprise Information Systems

166

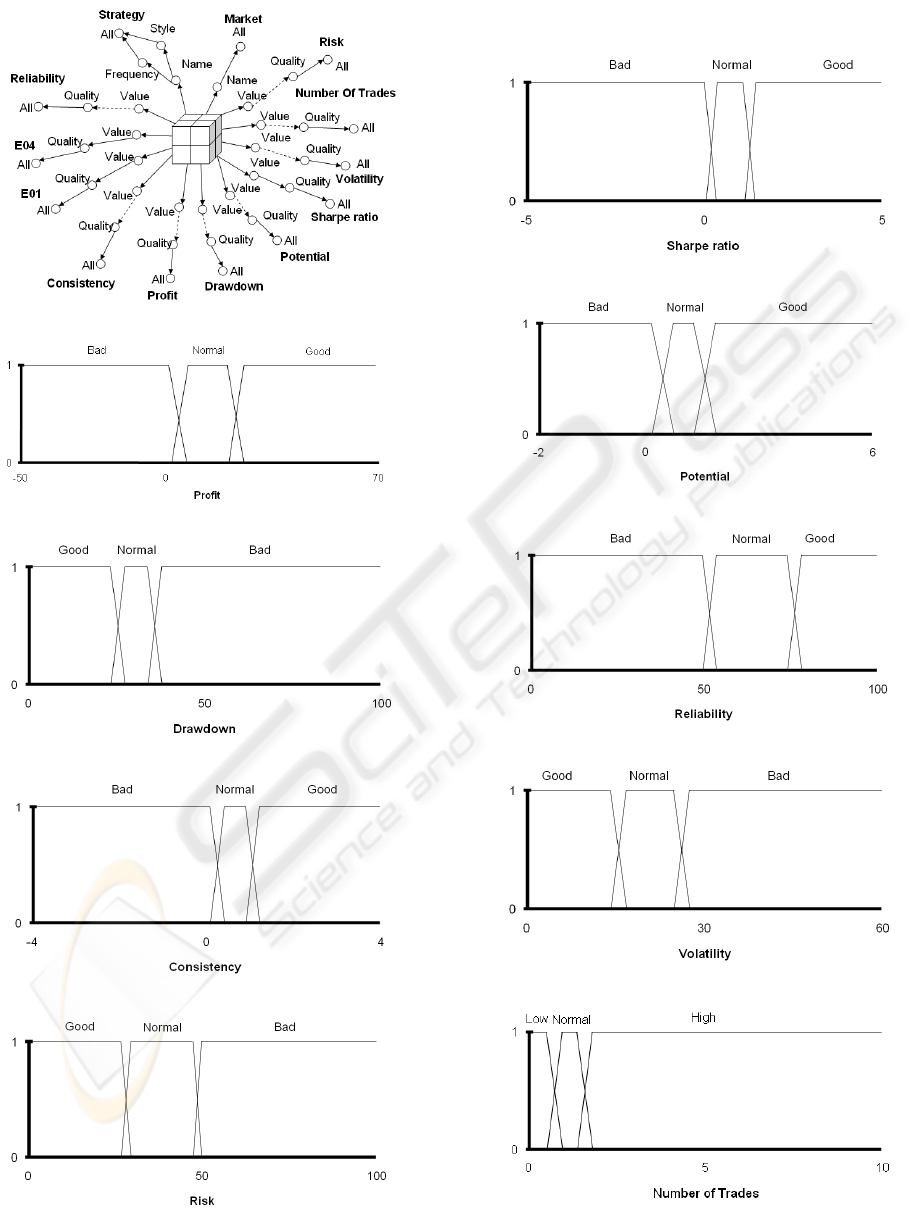
Figure 2: DataCube used in the analysis.

Figure 3: µ

Quality,Values

for Proﬁt dimension.

Figure 4: µ

Quality,Values

for Drawdown dimension.

Figure 5: µ

Quality,Values

for Consistency dimension.

Figure 6: µ

Quality,Values

for Risk dimension.

Figure 7: µ

Quality,Values

for Sharpe ratio dimension.

Figure 8: µ

Quality,Values

for Potential dimension.

Figure 9: µ

Quality,Values

for Reliability dimension.

Figure 10: µ

Quality,Values

for Volatility dimension.

Figure 11: µ

Range,Values

for Number of trades dimension.

USING FUZZY DATACUBES IN THE STUDY OF TRADING STRATEGIES

167

tive event occurring with how much damage this event

would case. It is measured in the interval [0,100], and

the high values represents high risk. Figure 6 shows

the classiﬁcation of the values in bad, normal or good

ones. The structure of the dimension is equal to the

previous ones presented.

Volatility: Volatility is the standard deviation of

the change in the value of a ﬁnancial instrument with

a speciﬁc time horizon. It is frequently used to quan-

tify the risk of the instrument during this time period.

Volatility is expressed in annualised terms. The val-

ues are in the interval [0,60] and we have divided it

into three different categories according to the mean-

ing of the values: good, bad and normal values. Fig-

ure 10 shows the kinship relations between the Values

and the Quality.

The structure of the dimension

is as follows: Volatility = ({Values,

Quality,All},≤

Volatility

,Values,All).

Number of Trades (Activity): This variable

models the number of trades per day. The values are

in the range [0,10]. We divide the interval in three cat-

egories: low, normal or high. The two extremes are

bad behavior and the center can be considered as nor-

mal, so we have a hierarchy with three levels and one

fuzzy relation between the base level (Values) and the

Range level. In this later case, the kinship relations

are presented in Figure 11 and the structure of the di-

mension is as follows: NumberOfTrades = ({Values,

Range, Quality, All},≤

NoT

,Values,All).

Market: The strategies can be used on different

markets and may present different behavior depend-

ing on it. We have considered the strategies in the fol-

lowing markets: CAC-40, DAX-50, Euronext, Ibex-

35 Nasdaq, Russell, name as CAC, DAX, EUR, IBX,

NDQ, USA, and RUS. No hierarchy has been deﬁne

over the markets, only to consider all the values to-

gether: Market = ({Name, All},≤

Market

,Name,All).

3.2 Measures

On this DataCube we have only considered one mea-

sure: the number of times the same coordinates (same

value in all the base levels of the dimensions) appear

in the data set.

3.3 DataCube

Finally, the structure of the DataCube is C

Trading

({Strategy, Proﬁt, Sharpe Ratio, Drawdown, Poten-

tial, Consistency, E01, E04, Risk, Volatility, Number

of trades, Market }, {Name, Values, Values, Values,

Values, Values, Values, Values, Values, Values, Val-

ues, Name, },Number

0,Ω,A), where A is the rela-

Figure 12: Proﬁt according to the risk.

tion that associates each fact with the corresponding

values of the base level of the dimensions. The Dat-

aCube has been ﬁlled with 3109 facts. In next section

we present some example queries over the structure

and brief comments of the results.

4 QUERIES

In this section we present two queries solved over

the DataCube built to show the advantages of using

a fuzzy model.

Query 1: We ﬁrst want to know if there is a rela-

tion between the proﬁt and the risk. The graph shown

in Figure 12 represents in the coordinate axis the cat-

egories for the proﬁt values and each one of the sub-

categories is the value for risk variable. The values

in Y axis are the number of times each combination

of values appears. According to the graph, it shows

a relationship between the values of both variables:

when the proﬁt is good most of the times the risk is

good too; the same as normal and bad categories. As

we have deﬁned the categories it means that for high

proﬁts the risk is low, and when the proﬁts are low

the risk is high, so there are an inverse relationship

between both variables.

Speaking about the imprecision, when the proﬁt

has good values the imprecision appears in good and

normal values, but very low for bad category, being

the highest one for normal values of proﬁt. This cir-

cumstance is due to values in the middle of both cat-

egories but nearer to the good one. In the case of

normal proﬁt we have most of the values in the nor-

mal risk subcategory with a higher imprecision than

in the others. Under this circumstance, we can say

that the values are around a normal risk. If we con-

sider a crisp model the values would belong to one of

the categories and we can not know the distribution

of the values inside the categories, so we do not have

this information for the analysis.

Query 2: The second query is intended to know

ICEIS 2007 - International Conference on Enterprise Information Systems

168

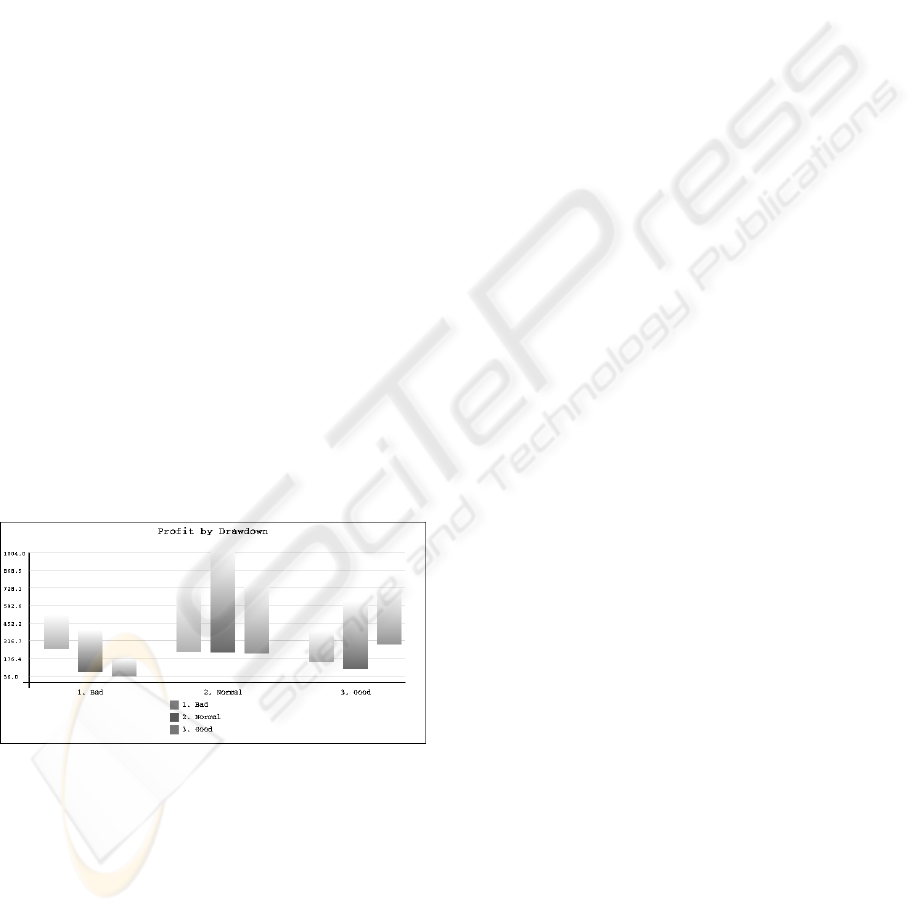
the relationship between the variables proﬁt and

drawdown. Figure 13 shows a graphic representation

of the facts of the resulting DataCube. In the graph the

coordinate axis represents the categories for the vari-

able proﬁt and each one of the subcategories shows

the number of times the strategies have this value ac-

cording to the quality in the variable drawdown. This

second query only present a signiﬁcative relationship

between the variables when the proﬁt is bad, due to

the higher the value of drawdown (bad values) the

higher is the number of the cases where the value of

proﬁt is bad. When the proﬁt belongs to category nor-

mal then all three categories in drawdown have values

very similar but with different imprecision. When the

proﬁt is good it seems that values are distributed near

the extreme subcategories (bad and good).

When considering the imprecision, the more sig-

niﬁcance cases are for normal and good categories

in proﬁt. When the values belong to normal, all

three subcategories for drawdown have high impre-

cision. This circumstance shows that the values are

distributed in the three categories, having an impor-

tant number of cases with values between two cate-

gories. When the drawdown belongs to normal the

imprecision is higher due to it considers values that

are between this category and the other two, mean-

while the other, the imprecision is the result of the

values between the own category and normal). When

the proﬁt is good the imprecision is centered in the

normal drawdown due to the values are distributed

mainly in the bad and good categories but with val-

ues near the normal one.

Figure 13: Proﬁt according to the drawdown.

As a result of the analysis of this query we get that

drawdown does not provide good information about

the expected proﬁt.

5 CONCLUSIONS

In this paper we have presented a fuzzy multidimen-

sional model as an exploratory analysis tool for study-

ing trading strategies. OLAP tools are suitable for

this kind of analysis and are able to work with a high

amont of data given an intuitive access for the user.

Using an OLAP system that implements a fuzzy mul-

tidimensional model allows to model some concepts

in a way closer to user perspective (e.g. values near

the average, etc.). In this situation to have an intuitive

way to show the results, that hides the complexity of

fuzzy logic, is very important.

We have model an economic problem using a

fuzzy multidimensional model that has enabled us to

use fuzzy concepts, to obtain analysis nearer to user,

and relax the edges of intervals, to reduce the edge

problem. Using the user views the model hides the

complexity of the model and gives graphic interpre-

tation for the queries. We have obtained coherent re-

sults for the queries and have shown that, in some situ-

ation, using fuzzy hierarchies is more informative for

the user, getting results that can not be obtained using

a crisp model, as the distribution of the values around

the edges of the categories.

REFERENCES

Blanco, I., S

anchez, D., Serrano, J. M., and Vila, M. A.

(2003). A new proposal of aggregation functions: The

linguistic summary. Lecture Notes in Computer Sci-

ence, 2715:127–134.

Codd, E. (1993). Providing OLAP (On-line Analytical Pro-

cessing) to user-analysts: An IT mandate. Technical

report, E.F. Codd and Associates.

Delgado, M., Molina, C., Rodr

ıguez-Ariza, L., S

anchez, D.,

J.M., and Vila, M. (2005). F-CubeFactory: A fuzzy

OLAP system for supporting imprecision. In IFSA

2005 World Congress: Fuzzy Logic, Soft Comput-

ing and Computational Intelligence, volume 1, pages

635–640, Beijing (China).

Delgado, M., Molina, C., S

anchez, D., Vila, M. A., and

Rodriguez-Ariza, L. (2004). A linguistic hierarchy for

datacube dimensiones modelling. In Current Ussues

in Data and Knowledge Engineering, pages 167–176,

Varsovia.

Molina, C., S

anchez, D., Vila, M. A., and Rodr

ıguez-Ariza,

L. (2006). A new fuzzy multidimensional model.

IEEE Transaction on Fuzzy Systems, 14(6):897–912.

USING FUZZY DATACUBES IN THE STUDY OF TRADING STRATEGIES

169