A NICHE BASED GENETIC ALGORITHM

FOR IMAGE REGISTRATION

Giuseppe Pascale and Luigi Troiano

RCOST - Faculty of Engineering, University of Sannio, Viale Traiano, Benevento, Italy

Keywords:

Image Registration, Genetic Algorithms.

Abstract:

Image registration aims to ﬁnd the unknown set of transformations able to reduce two or more images to a

common reference frame. Image registration can be regarded as an optimization problem, where the goal is to

maximize a measure of image similarity. The measure of similarity on the overall image can be computation-

ally expensive, leading to measure the similarity of smaller subimages. However, the reduction of subimage

size results into a higher multi-modality for the optimizing function. Recent investigations have shown that

genetic algorithms can address this problem. However, the simple scheme of genetic algorithms can still fall

in local optima. In this paper, we explore the application of niche-oriented genetic algorithms, showing their

strengths in providing a more effective image registration algorithm.

1 INTRODUCTION

Image registration is the process of overlaying one or

more images to a reference image of the same scene

taken at different times, from different viewpoints,

and/or by different sensors. It geometrically aligns

two images, namely the reference and the input im-

age. Differences between images are introduced due

to the different imaging conditions, such as a different

sensor position. In this case, image registration en-

tails with considering geometric transformations able

to compensate the sensor misalignment (Figure 1).

The registration process mainly consists in deter-

mining the unknown transformation parameters re-

quired to map the input image to the reference im-

age. The task of determining the best spatial trans-

formation for the image registration can be character-

ized by four main components (Brown, 1992): (i) the

feature space, (ii) the search space, (iii) the similar-

ity measure, and (iv) the search strategy. The feature

space represents the image content used to compare

the input and the reference images. The search space

is made by allowed transformations. The similarity

measure provides a quality index of each solution.

The normalized cross-correlation function is one of

the most used similarity measure and can be written

CC =

N−1

∑

i=0

N−1

∑

j=0

((R

− R) × (I

− I))

N−1

∑

i=0

N−1

∑

j=0

− R)

N−1

∑

i=0

N−1

∑

j=0

− I)

(1)

where N is the number of pixels, R

) is the pixel

of the reference (input) image at position i, j, and R

(I) is the pixel average value of the reference (input)

image. The time complexity of the normalized cross-

Figure 1: Image registration of satellite images considering

translations (tx,ty), rotation (r) and zoom (z).

342

Pascale G. and Troiano L. (2007).

A NICHE BASED GENETIC ALGORITHM FOR IMAGE REGISTRATION.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 342-347

DOI: 10.5220/0002382003420347

 SciTePress

correlation is O(N

). Although expensive, it is ranked

as one of most effective similarity measures. Because

it is computationally expensive, cross-correlation is

restricted to a subimage of input and reference im-

ages. The search strategy drives the exploration of

the search space. Which strategy to adopt depends on

characteristics of the similarity measure, the search

space and the feature space. Indeed, these three el-

ements determine the computational complexity and

shape the search space landscape.

Key issues in image registration techniques regard

accuracy and performances; in some applications reg-

istration accuracy is a key factor. For instance a study

presented by Townshend et al. (Townshend et al.,

1992) regarding the variation of land surfaces (mea-

sured using Normalized Difference Vegetation Index)

shows that a misregistration by only 1 pixel can intro-

duce error up to values higher than 50%.

This work focuses on image registration of two

satellite or airborne images, subject to small afﬁne

transformations, using a niche based Genetic Algo-

rithms (GA). We consider the set of image pixels

as feature space and afﬁne transformations as search

space. In order to evaluate the solution quality we

use a normalized cross-correlation similarity func-

tion. Genetic Algorithms help to explore the search

space efﬁciently and avoiding to be trapped in local

optima. The landscape multi-modality is emphasized

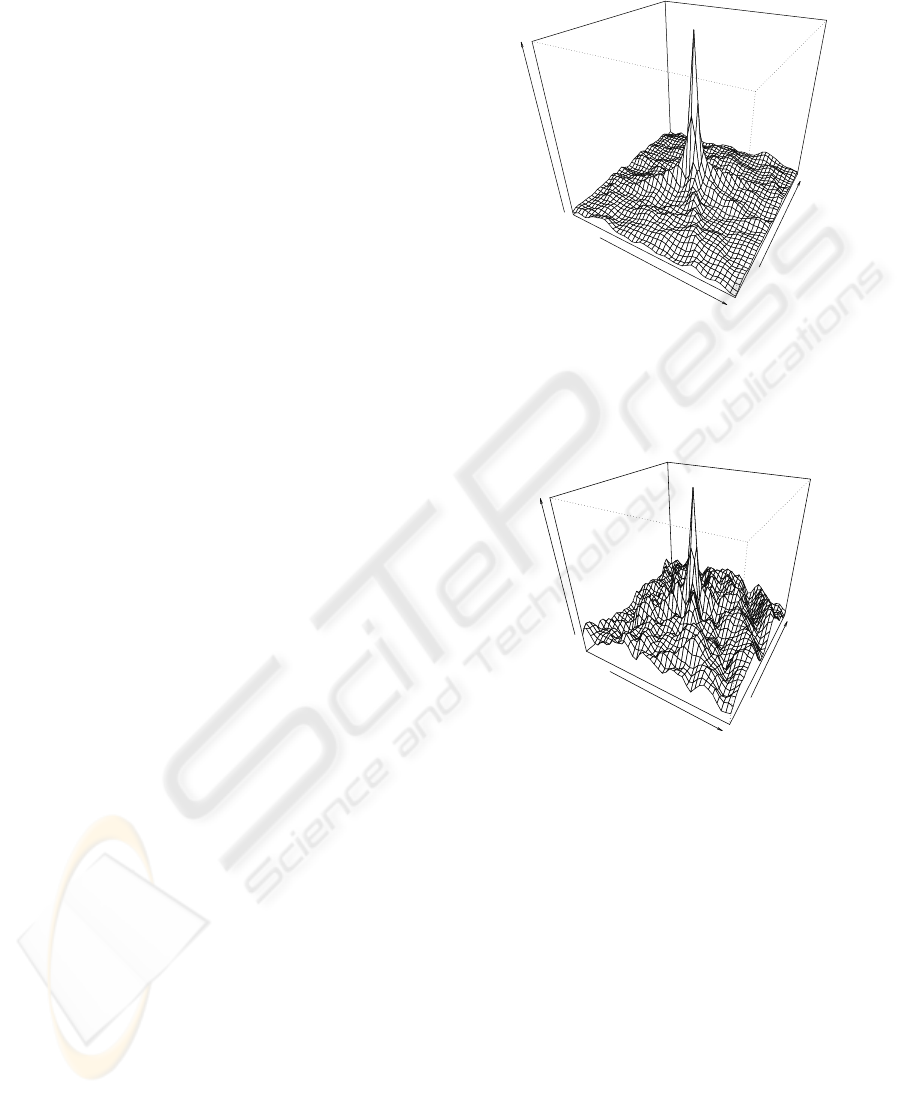
by the smaller sub-image size. This effect is depicted

by Figures 2 and 3. Although they only consider

translations, the landscape roughness becomes more

and more evident by reducing the image size. If we

consider these transformations jointly to others, such

as rotations and zooming, it appears evident that the

problem cannot be addressed effectively by linear op-

timizing techniques.

Several researchers applied GAs to image registra-

tion (Brown, 1992; Zitov

a and Flusser, 2003). Most

of them applied problem speciﬁc implementations of

genetic operators in Simple-GA. However, this algo-

rithm tends to converge to a single optimum, despite

of the landscape multi-modality. In order to cope with

this problem, niche oriented approaches have been

proposed in literature. Niche based GA represents

a more robust approach to search a multi-modal do-

main than traditional GA, since it provides a parallel

exploitation of search space portions. Moreover the

algorithm addresses the computational efﬁciency as it

is able to reach an optimal solution by fewer itera-

tions. Nevertheless, they have ever not been applied

to image registration. This paper aims to investigate

their application to this problem.

Section 2 describes the genetic algorithms consid-

ered by this paper, in particular the Simple-GA, and

translationY

translationX

Figure 2: Landscape of cross-correlation function using a

128× 128 sub-image - Translation along X end Y axes are

the only considered.

translationY

translationX

Figure 3: Landscape of cross-correlation function using a

32× 32 sub-image - Translation along X end Y axes are the

only considered.

two niche-oriented algorithms, i.e. Crowding-GA and

Sharing-GA. Section 3 presents some experimental

results. Conclusions and future work are outlined in

Section 4.

2 GENETIC ALGORITHMS

In this work we aim to compare niche oriented GA al-

gorithms to Simple-GA. In particular, two algorithms

are considered: (Deterministic) Crowding-GA and

Sharing-GA. Both are inspired by the niche exploita-

tion in nature, so that only similar individuals mate

and reproduce. Despite of the approach, the chromo-

some is always represented as a bit string. Each trans-

A NICHE BASED GENETIC ALGORITHM FOR IMAGE REGISTRATION

343

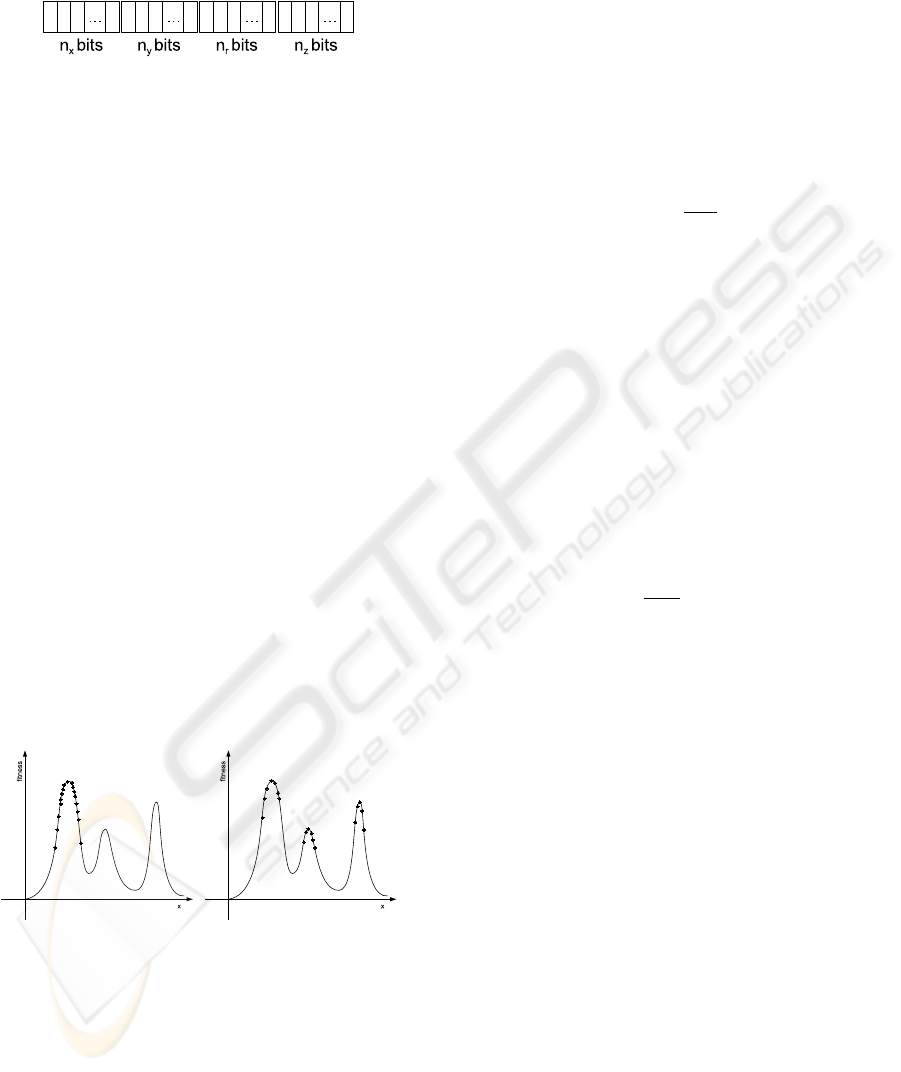
formation is coded by a ﬁxed-length bit sub-string, as

depicted in Figure 4.

Figure 4: The chromosome structure.

The number of bits representing each transforma-

tion depends on the transformation range, given the

precision (0.01 in our experimentation). Therefore

each substring represents a ﬁxed ﬂoating point real

number. The ﬁrst bit is used for coding the sign,

whilst the remaining bits represent the magnitude of

the transformation parameter.

The Simple-GA (Goldberg, 1989) is able to ex-

plore effectively a multimodal search space. How-

ever it tends to ﬁnd one single optimum, thus it can

still be trapped in local optima. This problem is the

result of genetic drift (De Jong, 1975), which is the

genetic algorithm’s tendency to select a population

with similar chromosomes, thus to converge towards

one solution. One strategy to overcome this problem

consists in maintaining population diversity, so that

different sub-populations are able to explore different

portions of the search space, in order to identify and

converge towards different multiple optima. Niche

based GAs represent an elegant and nature inspired

solution to address the issue of keeping the population

diversity. In a multimodal search space, each peak

can be thought of as a niche explored by a subpopula-

tion, similarly to nature where there are environments

(niches) that can support different types of life (Gold-

berg, 1989), as depicted in Figure 5.

Figure 5: The convergence of Simple-GA versus Niche-

GA.

In nature, a niche is able to support a certain num-

ber of individuals depending on the niche fertility and

the individual capacity of exploiting this fertility. If

there are too many individuals, the niche will not be

able to support all of them, and less competitive indi-

viduals are likely to die. Differently, if there are too

few individuals, they will start to reproduce quickly

in order to exploit the niche. Two of most success-

ful mechanisms are the ﬁtness sharing (Goldberg and

Richardson, 1987) and deterministic crowding (Mah-

foud, 1995).

The idea behind the sharing method is to reduce

the ﬁtness of individuals that are very similar in their

chromosome. By this way, individuals that uniquely

exploit portions of the search space are privileged for

reproduction, while discouraging redundant individ-

uals in the same area. The method is based on the

determination of the shared ﬁtness of the individual i

′

(i) =

f(i)

(2)

where f(i) is the individual’s raw ﬁtness, and m

is the

niche count, that is deﬁned as

∑

j=1

sh(d(i, j)) (3)

The sharing function sh depends on the distance (dis-

similarity) d(i, j) between the individual i and the in-

dividual j. It is a monotonically decreasing function,

so that the niche count is reduced if individuals are

closer. In particular, it returns 1 if the elements are

identical, and 0 if they exceed some threshold of dis-

similarity. The function originally proposed by Gold-

berg (Goldberg and Richardson, 1987) is deﬁned as

sh(d) =

(

1− (

)

if d < σ

0 otherwise

(4)

where d is the distance, α is a constant used to regu-

late the shape of the sharing function, and σ

the

dissimilarity threshold. When α = 1, the function is

triangular.

The chromosome similarity can be measured by

different metrics, aimed to measure the genotype or

phenotype similarity. A genotype similarity metric

is domain independent, as it considers the distance

between string coding of chromosomes, such as the

Hamming distance. A phenotype similarity is related

to the chromosome structure in genes and to their se-

mantic, thus it is domain speciﬁc. The main drawback

of the sharing approach is in estimating proper val-

ues for the sharing function parameters, moreover the

complexity for the ﬁtness evaluation becomes O(N

since a pairwise similarity measure is required at each

evaluation step.

The other mechanism for maintaining popula-

tion diversity is the determinist crowding (Mahfoud,

1992), that is an evolution of De Jong’s crowding

schema (De Jong, 1975). In De Jong’s schema, at

each generation only a portion of the population,

called population gap is selected for reproduction

ICEIS 2007 - International Conference on Enterprise Information Systems

344

(crossover and mutation). After reproduction, gen-

erated offsprings take the place of old individuals fol-

lowing this strategy: for each offspring a certain num-

ber of individuals are randomly selected from the pop-

ulation, and the most similar is the replaced by the

offspring. Similarity measures can be both genotypic

or phenotypic. The De Joung’s mechanism is thought

to reduce convergence of population to a single local

optimum. The drawback is that this algorithm slows

down the search space exploration.

In attempting to improve the De Jong’s schema,

Mahfoud suggests a new crowding schema called

Deterministic Crowding. In Mahfoud’s crowd-

ing schema, members are randomly chosen for

reproduction, then an offspring replaces a par-

ent only in case of higher ﬁtness. To deter-

mine which of the possible parent-offspring pair-

ing ({parent1-offspring1, parent2-offspring2} OR

{parent1-offspring2, parent2-offspring1}) should be

used in comparing the parents to the offsprings, the

total of the parent-offspring similarities for each of the

two possible combinations is determined. The parent-

offspring pair that has the highest total similarity is

used to determine if the offspring should replace the

parent. This allows to keep population diversity and

to efﬁciently explore the search space, as different in-

dividuals do not inﬂuence each other. Mahfoud also

discourages the use of genotypic similarity, in favor

of phenotypic similarity measure, as domain-speciﬁc

knowledge is able to better measure the similarity be-

tween individuals. Both assumptions result into better

performances.

3 EXPERIMENTATION

Although, niche based GAs promise to overpass

Simple-GA limitations, the successful application of

them depends on the problem characteristics. In this

section we report a summary of an experimentation

aimed to verify if the niche approach provides effec-

tive advantages to image registration.

Experimentation has been conducted applying

Table 1: Algorithm conﬁgurations.

Parameter Simple-GA Crowding-GA Sharing-GA

population 100 100 100

crossover

1.0 1.0 1.0

mutation

0.05 0.05 0.05

Elitism yes yes yes

coding binary MS binary MS binary MS

σ - - 2.0

α - - 1

distance - Phenotipic Phenotipic

Simple-GA, Crowding-GA and Sharing-GA to a 20

high resolution images. These are satellite or airborne

images of European cities acquired by different sen-

sors (see Table 2 for more details). Algorithms end

after 100 generations. Algorithm conﬁgurations are

summarized in Table 1. For each image 50 runs have

been performed, obtaining 1000 data points for anal-

ysis. The data ﬂow followed at each run is described

by Figure 6.

Figure 6: Experimentation steps.

The Quick Transform generates a misaligned in-

put image applying a random afﬁne transformation

to the reference image (linear interpolation is used).

Transformation components are generated assuming

a normal gaussian distribution (µ = 0, σ = 2.551), in

order to simulate a realistic sensor misalignment. The

range of misalignments are rotation = ±5

◦

, and trans-

lation = ±5 px. As scaling is particularly annoying

for image registration algorithms, we focused our at-

tention on it. We considered different scaling ranges

from [0.9,1.1] to [0.6,1.5]. A gray scale ﬁlter converts

the reference and input images to gray scale, in order

to make the registration more robust. An edge detec-

tion ﬁlter (e.g. Sobel’s ﬁlter) is also applied. The two

images are passed to the registration algorithm. Fi-

nally the registration solution is compared to the orig-

inal misaligning transformation in order to measure

accuracy, computed as the Pearson’s correlation co-

efﬁcient between the actual parameters a

act

and the

estimated parameters a

est

. This is akin to computing

the cosine of the angle between the parameters vec-

tors associated with the source and the target images.

ρ =

act

· a

est

)

act

k · ka

est

(5)

Correlation coefﬁcient is in [−1, 1]. Close to one cor-

relation coefﬁcients mean a small error between the

actual and the estimated parameters.

For practical purposes, a registration can be con-

sidered successfully executed, if the accuracy is over

a given threshold (0.8 in our experimentation.) The

percentage of tests providing an accuracy higher of

the threshold provides the algorithm success rate.

Figures 7 and 8 represent the success rate of the

three GA compared. The success rate analysis shows

A NICHE BASED GENETIC ALGORITHM FOR IMAGE REGISTRATION

345

Table 2: Images characteristics.

Image Acquisition Dimension Entropy(normalized)

Rome 1 Landsat 7 data (ETM+ bands 3, 2, and 1) 512× 512 0.622

Rome 2 ASTER (Terra) 512× 509 0.563

Venice Ikonos 512× 607 0.595

Naples Shuttle, Hasselblad camera with a 250 mm lens. 512× 512 0.508

London ASTER (Terra) 512× 366 0.503

Berlin ASTER (Terra) 512× 458 0.550

London Space photograph, Kodak 760C with 800 mm lens. 512× 384 0.554

Madrid ASTER (Terra) 512× 471 0.622

Athens Astronaut photograph, Kodak K60C with 400 mm lens 512× 471 0.616

Athens olympics Ikonos 512× 776 0.597

Bilbao ASTER (Infrared image) 512× 512 0.580

Madrid Photo Satellite Quickbird, Digital globe 1123× 512 0.641

Paris Infrared image from ASTER (Terra) 512× 443 0.543

Copenhagen Photo Satellite Quickbird, Digital globe 512× 512 0.626

Hamburg Photo Satellite Quickbird, Digital globe 512× 509 0.581

Brussels Photo Satellite Quickbird, Digital globe 512× 458 0.538

Paris Photo Satellite Quickbird, Digital globe 512× 512 0.559

that Crowding-GA is more accurate than Simple-GA,

as the related success rate is always higher. The bet-

ter performances are due to the capacity of crowding

of exploiting different niches, without being trapped

in any local optimum. Simple-GA instead tends to

converge to a single local optima, despite of multi-

modality of the search space.

The experimentation results provide also evidence

that the Crowding-GA is more robust than the Simple-

GA approach. Indeed using 64 × 64 subimages, then

increasing landscape multimodality, the Crowding-

GA success rate is subject to small reductions (3-

4% lesser than 128 × 128 case), whilst Simple-GA

performances are signiﬁcatively affected. Comparing

performances of algorithms with different subimage

sizes make this evident (Figure 9). Computationally,

the two algorithms are comparable.

The performance of Sharing-GA are intermediate

1.1 1.2 1.3 1.4 1.5

88 90 92 94 96 98

scaling()

success rate (%)

crowding

sharing

simple

Figure 7: Algorithms success rates using a 128× 128 sub-

image.

between Simple-GA and Crowding-GA. Similarly to

the Simple-GA, the Sharing-GA is less accurate and

robust than the Crowding-GA. However, it performs

slightly better than the Simple-GA. This is in accor-

dance with the beneﬁts expected by a niche based

algorithm. Weaker performances can be imputed to

sensitivity of the algorithms to parameters. Select-

ing proper values for the Sharing-GA parameters is

not a trivial process. Therefore, the need of a precise

calibration can be be considered as weakness of the

algorithm itself.

The experimentation has been conducted making

assumptions that could not be met in real applications.

Indeed, input image can differ from the reference im-

age due to morphological (e.g growth of vegetation)

or radiometric (e.g. images taken at different hours of

a day) changes. Also partial occlusions (e.g. clouds)

can occur in real cases. Such differences can be mis-

1.1 1.2 1.3 1.4 1.5

80 85 90 95

scaling()

success rate (%)

crowding

sharing

simple

Figure 8: Algorithms success rates using a 64 × 64 sub-

image.

ICEIS 2007 - International Conference on Enterprise Information Systems

346

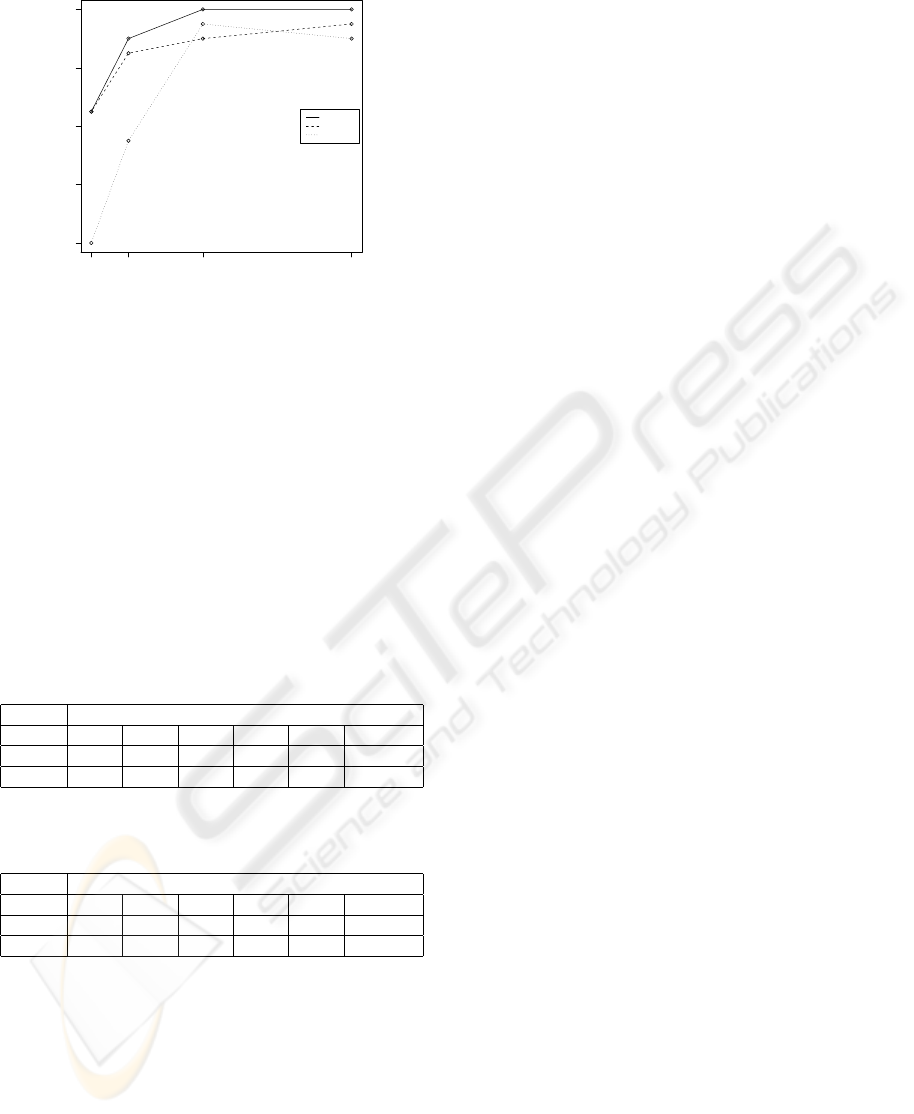
subimage size

success rate (%)

60 70 80 90 100

32 64 128 256

crowding

sharing

simple

Figure 9: Success rates of the three algorithms for different

sub-image sizes.

leading for a registration algorithm and should be con-

sidered in testing a registration algorithm. Another

approximation is that we do not take into considera-

tion perspective transformations. For satellite images,

however, this transformation can be ignored because

of the great distance. This effect is more relevant in

airborne images.

The better results obtained by Crowding-GA and

Sharing-GA are not due to the parameter conﬁgura-

tion. Indeed, in Table 3 and Table 4 we report perfor-

mances of Simple-GA with different parameter val-

ues.

Table 3: Success rate at different crossover rates.

Crossover probability (p

mutation

= 0.05)

Zoom 1.00 0.95 0.90 0.85 0.80 0.75

1.1 90.0 92.0 93.0 90.1 88.7 90.0

1.5 88.5 88.0 88.0 87.9 88.9 88.6

Table 4: Success rate at different mutation rates.

Mutation probability, (p

crossover

= 1.0)

Zoom 0.01 0.02 0.05 0.20 0.15 0.20

1.1 84.9 85.6 90.0 94.0 92.5 89.7

1.5 80.5 83.3 88.5 92.0 89.0 86.6

It results, that Sharing-GA and Crowding-GA out-

perform Simple-GA. Indeed success rate of Sharing-

GA is between 92.4 (zoom = 1.5) and 93.1

(zoom=1.1), whilst Crowding-GA success rate is 98.6

(zoom = 1.5) and 98.5 (zoom=1.1). In both cases the

result is better of Simple-GA performance. It worths

to notice that comparison is made with 128×128 sub-

image, thus entailing stronger landscape unimodality.

4 CONCLUSIONS AND FUTURE

WORKS

In this paper we investigated the application of niche

based genetic algorithms for image registration, as

an effective way to improve algorithm precision, in-

stead of adopting more complex genetic operators.

In particular, the paper described the use of two

niche based algorithms, namely the Sharing-GA and

the Crowding-GA. Experimentation has shown that

there is a real and consistent advantage in using the

Crowding-GA. The Sharing-GA, although conﬁrm-

ing the advantages provided by a niche approach, re-

sulted in lower performances, due the higher algo-

rithm sensitivity to parameter calibration.

Future work aims to extend the experimentation

in order to include some of the image differences that

can be encountered in real applications (i.e. photo-

metric and morphologic differences, occlusions, etc.).

Moreover some improvements can be obtained by

properly selecting the realignment region, according

to the entropy and other image characteristics.

REFERENCES

Brown, L. G. (1992). A survey of image registration tech-

niques. ACM Computing Surveys, 24:325–376.

De Jong, K. A. (1975). An analysis of the behavior of a

class of genetic adaptive systems. PhD thesis.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization and Machine Learning. Addison Wesley.

Goldberg, D. E. and Richardson, J. (1987). Genetic algo-

rithms with sharing for multimodal function optimiza-

tion. In Proc. of the II Int. Conf. on Genetic Algo-

rithms on Genetic Algorithms and Their Application,

pages 41–49, Mahwah, NJ, USA. Lawrence Erlbaum

Associates, Inc.

Mahfoud, S. W. (1992). Crowding and preselection revis-

ited. Parallel Problem Solving from Nature, 2:27–37.

Mahfoud, S. W. (1995). Niching methods for genetic al-

gorithms. Technical Report 1894, Department of

Computer Science, University of Illinois at Urbana-

Champaign, Urbana, Illinois.

Townshend, J. R. G., Justice, C. O., Gurney, C., and Mc-

Manus, J. (1992). The impact of misregistration on

change detection. IEEE Transaction on Geoscience

and Remote Sensing, 30(5):1054–1060.

Zitov

a, B. and Flusser, J. (2003). Image registration

methods: a survey. Image Vision Computation,

21(11):977–1000.

A NICHE BASED GENETIC ALGORITHM FOR IMAGE REGISTRATION

347