APPLICATION OF A GENETIC ALGORITHM TO A REAL

WORLD NURSE ROSTERING PROBLEM INSTANCE

Özgür Kelemci and A. Sima Uyar

Istanbul Technical University, İstanbul, Turkey

Keywords: Genetic algorithms, personnel scheduling, nurse rostering, constraint handling, real world problems.

Abstract: The nurse rostering problem involves assigning shifts to qualified personnel using a given timetable under

some hard and soft constraints. In this study, the nurse rostering problem instance of the Fatih Sultan

Mehmet Hospital is solved using a standard genetic algorithm. Currently, the rosters are being prepared by a

head nurse who performs this tedious task by hand. Due to the existence of many constraints, the resulting

schedules are usually suboptimal. The aim in this study is to generate better schedules. This paper reports

the results of the preliminary experiments for developing a good genetic algorithm for this problem.

1 INTRODUCTION

The nurse rostering problem (Burke et al., 2004)

belongs to a group of hard real world problems more

generally known as personnel scheduling. In the

nurse rostering problem, the aim is to assign shifts to

nurses who are qualified for the work they are

assigned to do. Traditionally, schedules are prepared

by hand. For automatic determination of the rosters,

several approaches exist in literature such as

evolutionary algorithms (Ahmad et al., 2000),

simulated annealing (Brusco and Jacobs, 1995), tabu

search (Burke and Soubeiga, 2003) and constraint

programming (Cheng et al., 1997).

In this study, the nurse rostering problem of the

Fatih Sultan Mehmet Hospital (FSMH) in Istanbul,

Turkey is solved using genetic algorithms (GA).

Currently, the head nurse in the hospital prepares the

monthly schedules for the three departments by hand

through “trial and error”. Due to the existence of

many hard and soft constraints, this procedure

usually gives under-optimal schedules. The aim of

the program developed in this study is to construct

the monthly schedules automatically using a GA.

The results of the experiments with a very basic

implementation of a GA with standard features are

very promising. Further research to improve the

solution quality is being conducted.

2 GENETIC ALGORITHMS

GAs (Eiben and Smith, 2003) are a form of

evolutionary algorithms which model mechanisms

and ideas from Mendel’s classical theory of genetics

and the Darwinist evolutionary theory. In this study,

a chromosome consists of the nurse schedules for all

the nurses in the three departments of the hospital.

Each day is represented as a gene which consists of

two integer parts: the department id of the nurse and

the shift type. There is a separate fitness calculation

function for each constraint which has a weight

assigned to it. The weighted sum of the fitness

scores for the constraints gives the overall fitness

score of the chromosome. The initial population is

created randomly. The reproduction step consists of

three stages: selection, crossover and mutation. In

this study, tournament selection, uniform crossover

and a random-resetting mutation is used. Trough a

pure generational replacement scheme, the

individuals to survive into the next generation are

determined.

3 THE NURSE ROSTERING

PROBLEM

In this study, the nurse rostering problem of the

Fatih Sultan Mehmet Hospital (FSMH) in Istanbul,

Turkey is solved. The actual data and the hard and

soft constraints for generating the schedules are

474

Kelemci Ö. and Sima Uyar A. (2007).

APPLICATION OF A GENETIC ALGORITHM TO A REAL WORLD NURSE ROSTERING PROBLEM INSTANCE.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 474-477

DOI: 10.5220/0002378204740477

 SciTePress

obtained from the hospital personnel and monthly

schedules are created automatically. The output of

the program determines the monthly schedules for

all 11 nurses. In this hospital, if necessary, transfer

of nurses between departments is possible.

There are four shift types. “Empty Shift”, “Day

Shift” and “Night Shift” (these shifts occurs during

the weekdays), “Combined Shift” (covers the whole

day and occurs only on the weekend days). There

are three departments: “Urology” and “Neurology”

are small departments as opposed to the “Internal

Medicine” department. The hard (“H”) and soft

(“S”) constraints are given below. The settings for

each constraint are determined based on historical

data of previous schedules obtained from the

hospital and on requirements stated by the head

nurse forming the schedules by hand. The schedules

are prepared monthly but for H1, H2 and H3, last

two days of the previous month are also considered.

Weekend Shift Distribution Constraint (H1):

Only one combined shift may be assigned for

consecutive weeks.

Off-Day Constraint (H2): If a nurse works a night

or a combined shift, an empty shift is assigned for

the next day.

Days between Shifts Constraint (H3): There

should be two days between two consecutive night

or combined shifts for each nurse.

Night and Combined Shift Staff Distribution

Constraint (H4): Exactly two nurses should be

assigned for each night and combined shift.

Repetition on Weekday Constraint (H5): At most

two night shifts can be assigned for the same

weekday in a month.

Weekend Shift Constraint (H6): Combined shifts

should not be assigned for the same day.

Lower Limit for Day Shift Distribution

Constraint (H7): At least 4 nurses for the internal

medicine and 1 nurse each for the smaller

departments should be assigned for each day shift.

Working Days for the 15-day Annual Leave

Constraint (H8): Night or combined shifts may be

assigned to the first Monday after the 15-days

annual leave and to the first Thursday before.

Off-Days for Annual Leave constraint (H9):

Combined shifts should not be assigned for the first

weekend after and the first weekend before the

annual leave.

Weekend Shift Distribution Constraint (S1): At

most 3 and at least 1 night and combined shifts can

be assigned to each nurse.

In Department Constraint (S2): Nurses of the

small departments should be assigned to their

departments for the day shifts. This constraint is

corrected by exchanging assignments with a nurse in

another department assigned to the same shift.

Night Shift Distribution Constraint (S3): Nurses

from the same small departments should not work in

the same night and combined shifts.

Weekend Pair Constraint (S4): Different

weekend-shift pairs should be assigned for

consecutive months.

Night Shift on Weekdays Constraint (S5): At most

5 and at least 1 night shifts can be assigned.

Working Days for the 5-day Annual Leave

Constraint (S6): Night or combined shifts may be

assigned to the first Monday and to the first

Thursday before the 5-days annual leave.

As stated before, the fitness of an individual is

the weighted sum of its penalty scores. In some of

the experiments, this value is used as it is and in

some, it is normalized. The objective is to minimize

the fitness value. The constraints have weights

associated with them. In the experiments section,

some of the experiments are conducted with

different fixed penalty weights for hard and soft

constraints. In the remaining experiments, adaptive

weights are used to change the weights assigned to

soft constraints in time. A change mechanism is

chosen such that in the beginning, the weights are

lower and they increase over time and the adaptive

weight function assigns a weight value between zero

and one as can be seen in Eq. 1 where E is the

adaptive weight constant.

weight = 1- e

-(Number of Current Generation/E)

(1)

4 EXPERIMENTS

The genetic algorithm setup used in all of the

experiment cases is given in Table-1.

18 different test scenarios are listed in Table-2.

In the table, the first column gives the test id and the

remaining columns either show whether the

corresponding operator/method is used in the test

case or not or give the corresponding value of a

parameter chosen for the specific test case. Case

results are listed in Table-3. α shows the percentage

of success over 50 runs. Success is defined as

obtaining a solution which is the global optimum,

i.e. has a total penalty score (fitness) of 0. β shows

the percentage of solutions over 50 runs which do

not violate any hard constraints but may or may not

APPLICATION OF A GENETIC ALGORITHM TO A REAL WORLD NURSE ROSTERING PROBLEM INSTANCE

475

violate some soft constraints. The numbers in the

remaining columns show the number of times the

corresponding constraint was violated over 50 runs.

Table 1: Genetic Algorithm Setup.

GA Type Generational

Chromosome Length (L) 11 * No of days in month

Population Size 330

Max No of Generations 5000

Crossover Uniform, rate=1

Mutation Traditional mutation, rate=1/L

Mate Selection Tournament selection, k=8

Hill Climbing Selection Tournament betw. 4 constraints

Run Count 50

Results show that C17 is the best test scenario in

terms of success ratio to get the best fitness value in

successful runs. In this test case, all operators and

mechanisms, i.e. adaptive soft constraint weights,

normalization of penalty scores, repair through hill

climbing and increased weight for the 3

hard

constraint (H3) are applied. There is only one

difference between case 7 and case 17, which is the

weight of the hard constraint H3. It was observed in

the initial testing stages that, considering the last two

days of the previous month causes more penalty

points for constraint H3 and is hard to resolve, so the

weight of H3 is increased (it is set to 10 as opposed

to 1 for all other hard constraints) in cases C17 and

C18 to remedy this problem. However, this increases

the penalty score of H4 and H2 in C17 and increases

the penalty score of some of the soft constraints in

C18. C18 is the best test scenario based on β.

It can be seen from the results that using the

repair method which basically is a hill climbing

operator, increases the success ratio. The

normalization method improves the success ratio.

The adaptive weight method increases the weight of

the soft constraints exponentially, so the penalty

points of soft constraints decrease, but this affects

hard constraints due to the fact that the relative

effect of the weights of the hard constraints on the

overall fitness also decreases.

5 CONCLUSION AND FUTURE

WORK

A real world instance of the nurse rostering problem

is solved using mostly a standard GA. Actual data

and hard and soft constraints have been obtained

from a hospital (FSMH in Istanbul, Turkey) where

currently the head nurse of the hospital is preparing

the schedules by hand. The effect of two constraint

handling methods, a repair technique, normalization

of fitness values and parameter settings for these are

explored in this study. As a result of the

experiments, it is seen that normalization of the

penalty scores, repairing of constraint violations and

using adaptive weights for the constraints are all

useful to obtain good results. During the

experiments trying to satisfy the hard constraint (H3)

which seemed to be a problematic constraint, it is

seen that it could also be useful to give different

weights to different constraints. It would be

worthwhile to explore this in the future.

Since this study aims to solve a real world

problem, it is expected that it answers all the

requirements of the hospital personnel for which it is

designed. This study presents the results of

preliminary experiments. Even though a very

standard GA is used, the results are quite promising.

After further experiments with fine tuning the

current approach, experiments with more

sophisticated GAs will be performed. Further work

is currently being conducted to address these issues.

REFERENCES

Burke, E. K., de Causmaecker, P., vanden Berghe, G.,van

Landeghem, H., 2004. ”The State of the Art of Nurse

Rostering”. 7:411—499. Kluwer.

Ahmad, J., Yamamoto, M., Ohuchi A., 2000.

“Evolutionary Algorithms for Nurse Scheduling

Problem”, Proc. of IEEE Congress on Evolutionary

Computation, 196—203.

Brusco, M. J., Jacobs, L. W., 1995. “Cost Analysis of

Alternative Formulations for Personnel Scheduling in

Continuously Operating Organizations”. European J.

of Operational Research, 86:249—261.Elsevier.

Burke, E., Soubeiga, E., 2003. ”Scheduling Nurses using a

Tabu-Search Hyperheuristic”, Proc. of MISTA, 197—

218.

Cheng, B.M.W., Lee, J.H.M., Wu, J.C.K.,1997. “A Nurse

Rostering System using Constraint Programming and

Redundant Modelling”, IEEE Trans. On Information

Technology in Biomedicie, 1(1):44—54.

Eiben, A. E., Smith, J. E., 2003. Introduction to

Evolutionary Computing, Springer.

ICEIS 2007 - International Conference on Enterprise Information Systems

476

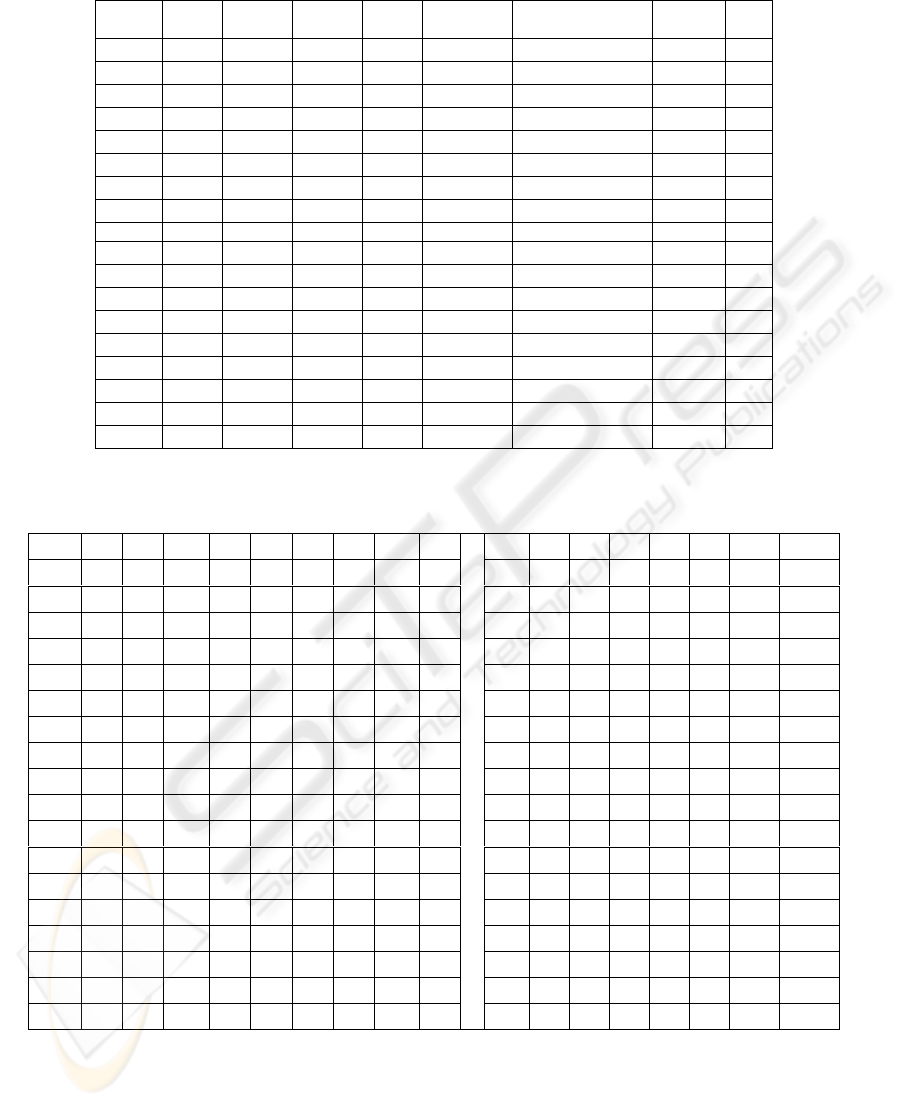
Table 2: Description of the test cases.

Cases

Adap

tive

Norma

lization

Repair

Exch

ange

Soft/Hard

Weight

Constraint S6

(Low/High Limit)

Weight

C1 No No No No 0.1/1 1/5 1 -

C2 No No Yes No 0.1/1 1/5 1 -

C3 No Yes Yes No 0.1/1 1/5 1 -

C4 Yes No Yes No (0.02-1)/1 1/5 1 500

C5 Yes Yes Yes No (0.02-1)/1 1/5 1 500

C6 No No Yes Yes 0.1/1 1/5 1 -

C7 Yes Yes Yes Yes (0.02-1)/1 1/5 1 500

C8 No Yes Yes Yes 0.1/1 1/5 1 -

C9 Yes Yes Yes Yes (0.02-1)/1 1/5 1 100

C10 No Yes Yes Yes 0.1/1 1/5 1 -

C11 Yes Yes Yes Yes (0.02-1)/1 2/3 1 500

C12 No Yes Yes Yes 0.1/1 2/3 1 -

C13 Yes Yes Yes Yes (0.02-1)/1 2/3 1 500

C14 No Yes Yes Yes 0.1/1 2/3 1 -

C15 No Yes Yes Yes 0.1/1 2/3 1 -

C16 No Yes Yes Yes 0.1/1 1/5 1 -

C17 Yes Yes Yes Yes (0.02-1)/1 1/5 10 500

C18 No Yes Yes Yes 0.1/1 1/5 10 -

Table 3: Results of the tests for all test cases.

H1 H2 H3 H4 H5 H6 H7 H8 H9 S1 S2 S3 S4 S5 S6 α β

C1 8 1 1 36 - 1 - - - 17 45 29 48 3 - 0.00 0.20

C2 - - - 1 - - - - - 4 20 1 24 - - 0.26 0.98

C3 - - 15 - - - - - - 3 11 5 3 - - 0.48 0.70

C4 - - - 27 - 2 - - - 10 45 18 37 2 - 0.02 0.36

C5 - - 26 - - - - - - - - - - - - 0.48 0.48

C6 - - - - - - - - - 1 4 4 21 - - 0.46 1.00

C7 - - 18 - - - - - - - - - - - - 0.64 0.64

C8 - - 9 - - - - - - 3 3 3 - - - 0.74 0.82

C9 - 2 22 2 - - - - - - - - - - - 0.56 0.56

C10 - - 4 - - - - - - 2 2 3 12 - - 0.58 0.92

C11 - 1 34 3 - - - - - - - - - - - 0.32 0.32

C12 - - 10 - - - - - - 1 5 3 3 15 - 0.42 0.80

C13 - 4 38 4 - - - - - - - - - - - 0.24 0.24

C14 - - 3 - - - - - - 4 4 2 13 6 - 0.52 0.94

C15 - - 27 1 - - - - - 1 - - - 1 - 0.42 0.44

C16 - - 23 - - - - - - - - - - - - 0.54 0.54

C17 - 2 - 18 - - - - - - - - - - - 0.78 0.78

C18 - - - - - - - - -

4 3 1 12 - - 0.70 1.00

APPLICATION OF A GENETIC ALGORITHM TO A REAL WORLD NURSE ROSTERING PROBLEM INSTANCE

477