OBTAINING AND EVALUATING GENERALIZED ASSOCIATION

RULES

Veronica Oliveira de Carvalho

Student of S

ao Paulo University, S

ao Carlos, S

ao Paulo, Brazil

Professor of Centro Universit

ario de Araraquara, Araraquara, S

ao Paulo, Brazil

Solange Oliveira Rezende, M

ario de Castro

Computer and Mathematics Science Institute, S

ao Paulo University

400 Trabalhador S

ao-Carlense Avenue, S

ao Carlos, Brazil

Keywords:

Generalized association rules, objective evaluation measures, rule quality evaluation.

Abstract:

Generalized association rules are rules that contain some background knowledge giving a more general view

of the domain. This knowledge is codiﬁed by a taxonomy set over the data set items. Many researches

use taxonomies in different data mining steps to obtain generalized rules. So, this work initially presents an

approach to obtain generalized association rules in the post-processing data mining step using taxonomies.

However, an important issue that has to be explored is the quality of the knowledge expressed by generalized

rules, since the objective of the data mining process is to obtain useful and interesting knowledge to support

the user’s decisions. In general, what researches do to help the users to select these pieces of knowledge is

to reduce the obtained set by pruning some specialized rules using a subjective measure. In this context, this

paper also presents a quality analysis of the generalized association rules. The quality of the rules obtained

by the proposed approach was evaluated. The experiments show that some knowledge evaluation objective

measures are appropriate only when the generalization occurs on one speciﬁc side of the rules.

1 INTRODUCTION

The use of background knowledge in the data mining

process allows the discovery of more abstract, com-

pact and, sometimes, interesting knowledge. An

example of background knowledge can be a concept

hierarchy, that is, a structure in which high level

abstraction concepts (generalizations of low level

concepts) are hierarchically organized by a domain

expert or by an automatic process. An example of

a simple concept hierarchy is taxonomy. Taxonomies

reﬂect arbitrary individual or collective views accor-

ding to which the set of items is hierarchically orga-

nized (Adamo, 2001).

One of the descriptive tasks in data mining is asso-

ciation rule (AR), which was introduced in (Agrawal

and Srikant, 1994). Since this technique generates all

possible rules considering only the items contained in

the data set, which leads to specialized knowledge,

the generalized association rules (GAR), which are

rules composed by items contained in any level of

a given taxonomy, were introduced by (Srikant and

Agrawal, 1995).

Taxonomies can be used in the different steps of

the data mining process. Nowadays, there are many

works that propose to obtain GAR in the mining step

as (Srikant and Agrawal, 1995; Srikant and Agrawal,

1997), (Hipp et al., 1998), (Weber, 1998), (Baixeries

et al., 2000), (Yen and Chen, 2001) and (Sriphaew

and Theeramunkong, 2004) and in the pre-processing

step as (Han and Fu, 1995; Han and Fu, 1999). There

are some approaches that apply taxonomies in the

post-processing step, focus of our work. (Chung and

Lui, 2000) propose a post-processing approach that

obtains GAR with different levels of support. (Huang

and Wu, 2002) propose an algorithm that considers as

input a data set, a set of large itemsets, a specialized

AR set (a set composed by rules that only contains

leaf taxonomy items) and a taxonomy set. Based on

these inputs, an association graph is obtained. This

graph represents the existing associations among the

items contained in the taxonomy. Based on this graph

310

Oliveira de Carvalho V., Oliveira Rezende S. and de Castro M. (2007).

OBTAINING AND EVALUATING GENERALIZED ASSOCIATION RULES.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 310-315

DOI: 10.5220/0002367703100315

 SciTePress

and, considering some pruning techniques, the algo-

rithm obtains all the GAR.

A problem identiﬁed in some of the works men-

tioned above is related to the number of rules ob-

tained: the sets containing GAR are larger than the

AR sets generated without taxonomies. It is known

that although the AR technique is very useful, it

has the disadvantage of generating a large number

of rules, making the user’s interpretation difﬁcult.

Therefore, it is more difﬁcult to analyze a GAR set

due to the huge number of rules.

Considering this context, in (Domingues and

Rezende, 2005) an algorithm is proposed to obtain

a GAR set that decreases or keeps the volume of a

specialized AR set. The work proposed here is an

extension of the work presented in (Domingues and

Rezende, 2005). The idea of the approach presented

here, called GARPA (Section 2), is shown in Figure 1.

It is supposed that the elements shown inside the dot-

ted box are available, such as an AR set formed only

by specialized rules, the data set used to generate the

specialized rules and the taxonomies. Based on these

inputs GARPA obtains a GAR set composed by some

specialized rules that could not be generalized (for

example, rule R40 shown in Figure 1) and by gene-

ralized rules obtained by grouping some specialized

rules using the taxonomies (for example, rule R35

shown in Figure 1 – rule obtained by grouping the

rules milk

⇒ bread (R3), milk

⇒ bread (R4) and

milk

⇒ bread (R7)). Along with the GAR set there

is a list that identiﬁes the participation of each specia-

lized item in the general items (see Section 2). It is

important to note that our approach (GARPA) has ba-

sically ﬁve differences from the approach proposed by

(Domingues and Rezende, 2005): (a) generalization

does not occur on only one side of the rule, but also

on both sides; (b) generalization does not only occur

among the rules, but also among the items of the rules;

for each of the items contained in the taxonomy; (d)

generalization occurs even if one rule possesses more

than one item with the same ancestor; (e) a genera-

lized rule will be valid only if its support/conﬁdence is

higher than t% of the highest value of the same mea-

sure in its specialized rules.

An important aspect that has to be mentioned

with respect to GAR is that the most of the works

found in literature only realizes a performance study

of their proposed approaches. However, more im-

portant than performance is the quality of the ex-

tracted rules. What some researches do – (Srikant and

Agrawal, 1995; Srikant and Agrawal, 1997), (Adamo,

2001), (Han and Fu, 1999) – is to prune all specialized

rules only if they have a behavior that differs signiﬁ-

cantly from their generalizations. To identify the size

of this difference, the user has to inform a β threshold

value in order to know how many β times the specia-

lized rule has to be different from the generalized rule.

Since the choice of the β threshold is subjective, it is

difﬁcult to use this kind of pruning. In addition, this

methodology is used with the purpose of reducing the

association rule set obtained and not in analyzing the

quality of the rules. In this context, an analysis to

evaluate a GAR set using objective evaluation mea-

sures is also presented.

The paper is organized as follow. Section 2

presents the proposed approach to obtain generalized

rule sets. Section 3 presents the data sets used in the

knowledge quality experiments. Section 4 presents

the quality analysis considering some objective mea-

sures. Finally, Section 5 presents the paper conclu-

sions.

2 THE GENERALIZED

ASSOCIATION RULE

POST-PROCESSING

APPROACH (GARPA)

The aim of GARPA is to post-process specialized AR

using taxonomies in order to obtain a reduced and

more expressive set of AR that facilitates the user’s

comprehension. The GARPA methodology is struc-

tured in Algorithm 1. The main idea consists of ge-

neralizing a set of specialized AR, obtained with a

traditional rule extraction algorithm, based on a ta-

xonomy set given by a domain expert. The rule ge-

neralization can be done on one side of the rule (an-

tecedent (lhs: left hand side) or consequent (rhs: right

hand side)) or on both sides (lrhs: left right hand

side) (option Side in Figure 1). In GARPA, genera-

lized rules can be generated without the use of all the

items contained in taxonomy. For example: suppose

the rule milk ⇒ bread represents a generalized rule

and that milk is represented in taxonomy by milk

milk

, milk

and milk

. The rule milk ⇒ bread

will be generalized even if there isn’t a rule for each

kind of milk. Thus, in order to guide the user’s com-

prehension of generalized rules, a list with the partici-

pation of each specialized item in the general items is

generated. For the rule described above, the list pre-

sented in Figure 1 would be generated.

This is one of the advantages of GARPA: using

taxonomies that contain knowledge from the same

domain. Consider a taxonomy that has knowledge

about foodstuff. Any data set that contains informa-

tion about these products can use the same taxonomy

OBTAINING AND EVALUATING GENERALIZED ASSOCIATION RULES

311

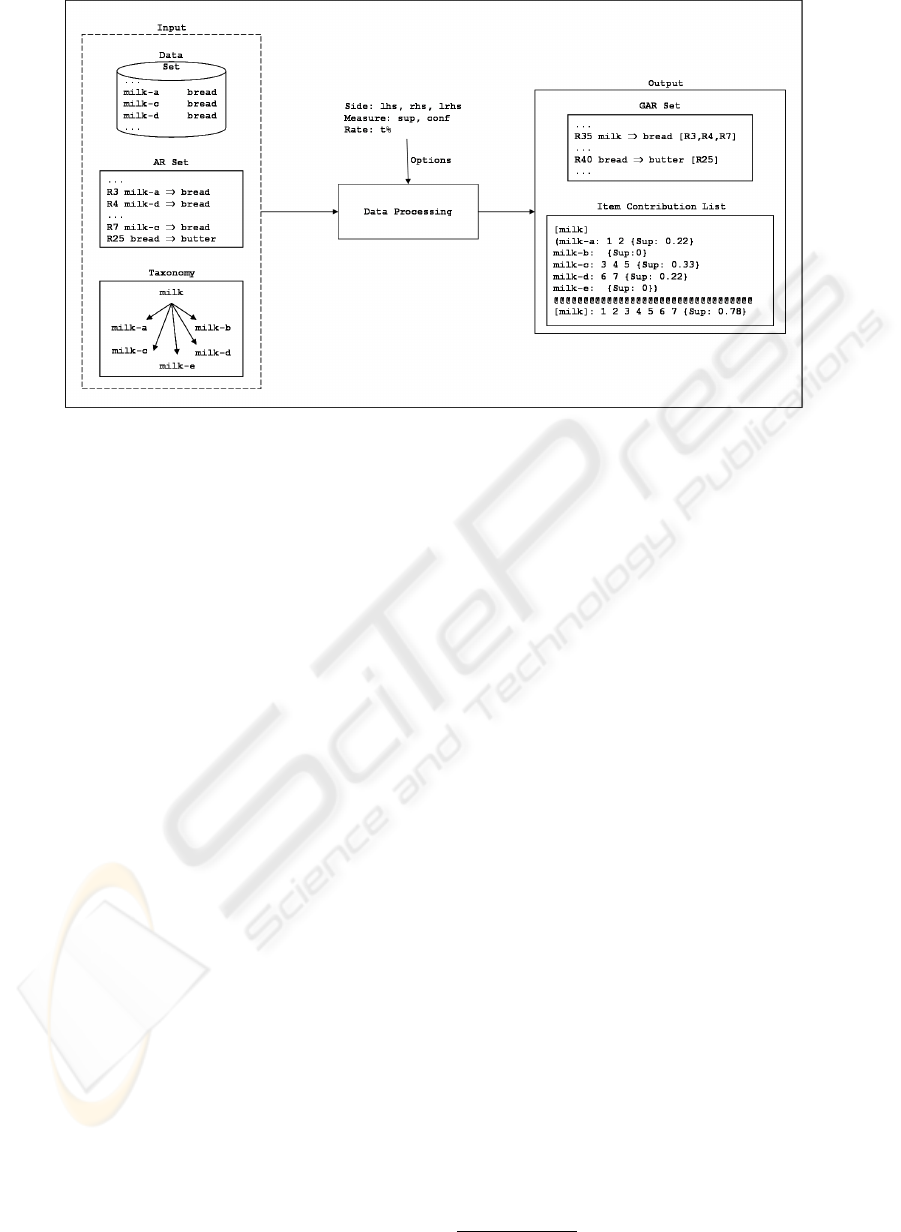
Figure 1: The idea of GARPA approach.

in the generalization process, given that for each ge-

neralized rule the support of each specialized item is

identiﬁed through a list. This means that if an item

contains 0% support this item was not present in the

transactions and therefore did not contribute to the ge-

neralization process.

As all the generalized rules can be generated with-

out the presence of all items from the taxonomy, to

avoid an over-generalization, a set of specialized rules

can be substituted only by a more general rule if the

support (sup) or the conﬁdence (con f ) of this rule

(option Measure in Figure 1) is t% higher than the

highest value of the same selected measure in the

specialized rules (option Rate in Figure 1). This cri-

terion can be viewed as an implicit variation of the

support/conﬁdence framework that is explicitly used

in some of the works mentioned in Section 1.

3 SETS CONSIDERED IN THE

QUALITY ANALYSIS

As stated before, more important than analyzing the

performance of a GAR approach is to analyze the

quality of the extracted rules. So, in order to evaluate

the knowledge expressed by generalized rules, an ex-

periment was built to obtain some GAR sets for two

different data sets. The ﬁrst data set (DS-1) contains

a one day sale of a supermarket located in So Car-

los city. DS-1 contains 1716 transactions with 1939

distinct items. The second data set (DS-2) is avai-

lable in the R Project for Statistical Computing

. The

groceries data set contains one month (30 days) of

real-world point-of-sale transaction data from a typi-

cal grocery outlet. DS-2 contains 9835 transactions

with 169 distinct items.

As described before, the ﬁrst step in GARPA, as

shown in Figure 1, needs a specialized rule set, that

was obtained here by the traditional Apriori mining

algorithm, and a taxonomy set. Thus, four taxonomy

sets were constructed for each data set, distributed

in the following way: one set composed by taxono-

mies containing one level (1L) of abstraction; one

set composed by taxonomies containing two levels

(2L) of abstraction; one set composed by taxonomies

containing three levels (3L) of abstraction; one set

composed by taxonomies containing different levels

(DL) of abstraction. Considering all possible combi-

nations between the generalization side and the taxo-

nomy level, twelve GAR sets were generated through

GARPA for each data set. Using the notation side-

level (of the taxonomy), the twelve combinations con-

sidered to obtain the twelve GAR sets for each data

set were: (a) lhs-1L; (b) rhs-1L; (c) lrhs-1L; (d) lhs-

2L; (e) rhs-2L; (f) lrhs-2L; (g) lhs-3L; (h) rhs-3L; (i)

lrhs-3L; (j) lhs-DL; (k) rhs-DL; (l) lrhs-DL. Toward

the measure and rate options (Figure 1), in all experi-

ments (a to l) the support (sup) measure with a rate

of 0% was used, since this conﬁguration presented

a better performance in relation to the conﬁgurations

using the conﬁdence (con f ) measure. This means that

the sup-0% conﬁguration produced the most reduced

Available for download in www.r-project.org.

ICEIS 2007 - International Conference on Enterprise Information Systems

312

Algorithm 1 Generalization Algorithm.

Input: data set D, set R of association rules in the sintax

standard, set of taxonomies T , side L of the rule to be

generalized (lhs, rhs, lrhs), measure M to be used in the

generalization (su p, con f ), rate t of the measure M.

Output: set RGen of generalized association rules and list Contrib

with the participation of each specialized item in the general

item.

1: Contrib := calculate-item-contribution(D,T );

2: RGen := R; NATax := 1;

3: if ((L = lhs) OR (L = rhs)) then

4: SC1 := generate-initial-subsets(R,

L);

5: forall (

SC1 > 2,

SC1 ⊆ SC1) do

6: while (NATax 6 NMTax) do

7: substitute-items(

SC1,L,NATax);

8: remove-repeated-items(

SC1,L);

9: lexicographically-organized(

SC1,L);

10: SC2 := generate-subsets(

SC1,L);

11: forall (

SC2 > 2,

SC2 ⊆ SC2) do

12: r := rule(

SC2);

13: valid-rule := evaluate-generalization-criteria(r);

14: if valid-rule then

15: calculate-contingency-table(r);

16: valid-rule := check-measure-criterion(r,M,t);

17: if valid-rule then

18: RGen := RGen ∪ {r};

19: RGen := remove-source-rules(r,RGen);

20: end-if

21: end-if

22: end-for

23: NATax := NATax + 1;

24: end-while

25: end-for

26: end-if

27: if (L = lrhs) then

28: TempRules := R;

29: while (NATax 6 NMTax) do

30: substitute-items(TempRules,L,NATax);

31: remove-repeated-items(TempRules,L);

32: lexicographically-organized(TempRules,L);

33: SC1 := generate-subsets(TempRules,L);

34: forall (

SC1 > 2,

SC1 ⊆ SC1) do

35: r := regra(

SC1);

36: valid-rule := evaluate-generalization-criteria(r);

37: if valid-rule then

38: calculate-contingency-table(r);

39: valide-rule := check-measure-criterion(r,M,t);

40: if valid-rule then

41: RGen := RGen ∪ {r};

42: RGen := remove-source-rules(r,RGen);

43: end-if

44: end-if

45: end-for

46: NATax := NATax + 1;

47: end-while

48: end-if

49: RGen := remove-repeated-rules(RGen);

50: RGen := syntax-standard(RGen);

GAR sets. However, the explanation referring to the

difference performance that occurred between the two

measures using different rates values is not going to

be done, since the reduction rate is not the focus of

this paper; the focus is the rule quality.

4 ANALYZING GAR THROUGH

OBJECTIVE MEASURES

According to the GARPA methodology, for each rule

contained in a GAR set its base rules are identi-

ﬁed, that is, the rules that were grouped by taxo-

nomy to obtain the generalized rule. Based on this

fact, the quality of a generalized rule can be com-

pared with the quality of its base rules considering

an objective evaluation measure. To evaluate the

quality of a GAR, all the objective evaluation mea-

sures described in (Tan et al., 2004) were used:

Added Value (AV), Certainty Factor (CF), Collective

Strength (CS), Conﬁdence (Conf), Conviction (Conv),

Cosine (Cos), φ-coefﬁcient (φ), Gini Index (GI), J-

Measure (JM), Jaccard (ζ), Kappa (κ), Klosgen (Kl),

Goodman-Kruskal’s (λ), Laplace (L), Interest Factor

(IF), Mutual Information (MI), Piatetsky-Shapiro’s

(PS), Odds Ratio (OR), Yule’s Q (YQ) and Yule’s Y

(YY). So, an analysis was carried out to verify if the

generalized rules maintain or improve its measures

values compared to its base rules. Suppose, for exam-

ple, that the generalized rule bread

⇒ milk was ge-

nerated by the rules bread

⇒ milk

, bread

⇒ milk

and bread

⇒ milk

. For each considered measure, a

count was carried out to ﬁnd the percentage where-

upon a generalized rule had a value equal or greater

than the values of its base rules. For example, if the

rule bread

⇒ milk had a value of 0.63 for a spe-

ciﬁc measure and the rules bread

⇒ milk

, bread

⇒

milk

and bread

⇒ milk

the values 0.53, 0.63 and

0.77 respectively, for the same speciﬁc measure, the

percentage would be 66.67% (2/3 – of a total of three

rules, two of them had a smaller value than its gene-

ralized rule). This percentage was calculated for each

generalized rule contained in each of the twenty-four

(twelve for each data set) generalized rule set and the

results were plotted in a histogram as in Figure 2. The

x axis represents the ranges that varies from 0.0 (0%)

to 1.0 (100%). For example, a range from 0.5 to 0.6

indicates that a generalized rule contains, in 50% to

60% of the times, a value greater or equal to its base

rules. The y axis represents the percentage of genera-

lized rules that belongs to a speciﬁc range. For exam-

ple, in Figure 2(a) 98.39% of the generalized rules be-

long to the 0.9-1.0 range, indicating that in almost all

the cases (98.39%) the generalized rules maintained

or increased its value compared to almost all its base

rules (90% to 100%).

In order to analyze the results, Table 1 was ge-

nerated. (Only a piece of the results are presented

in Table 1 due to space). Considering each measure

and each of the twelve GAR sets related to each data

set, the percentage of rules belonging to the 0.9-1.0

range was observed. It is important to note that this

range indicates that a generalized rule contains, in

90% to 100% of the times, a value greater or equal

to its base rules. This value indicates that, for exam-

ple, in 98.39% of the times in DS-1, using the rhs-1L

option and the Added Value measure (the ﬁrst value

indicated in gray), the generalized rules had, in the

0.9-1.0 range, a value greater or equal to its base rules.

OBTAINING AND EVALUATING GENERALIZED ASSOCIATION RULES

313

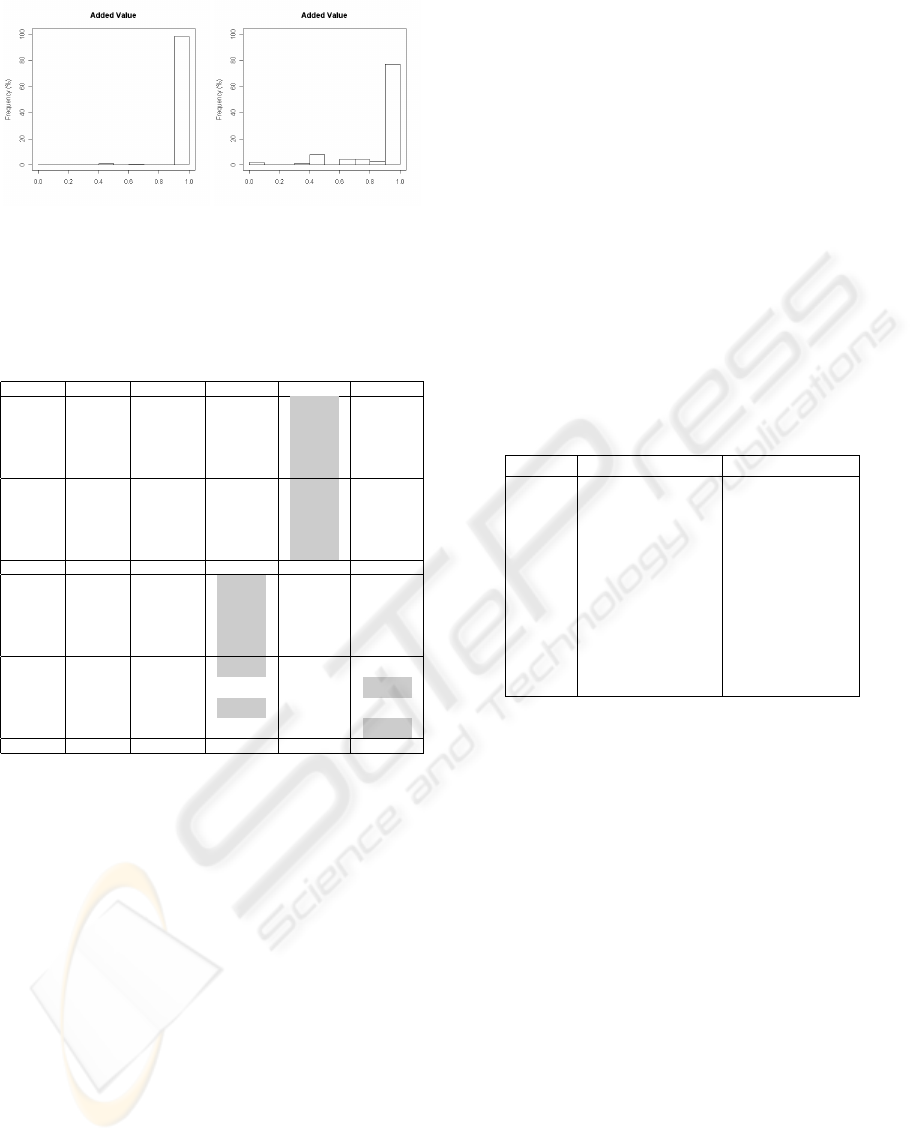
(a) DS-1:rhs-1L (b) DS-2:rhs-1L

Figure 2: Histogram for the Added Value measure consi-

dering the rhs-1L option.

Table 1: Percentage of generalized rules belonging to the

0.9-1.0 range considering each measure and each GAR set.

Measure Data Set Tax. Level lhs rhs lrhs

AV DS-1 1L 3.33% 98.39% 49.84%

2L 1.22% 97.27% 37.63%

3L 0.77% 82.01% 30.59%

DL 2.18% 78.49% 29.94%

AV DS-2 1L 2.07% 77.10% 33.33%

2L 2.02% 84.47% 38.11%

3L 2.12% 83.25% 35.95%

DL 1.99% 84.82% 37.12%

... ... ... ... ... ...

CS DS-1 1L 89.88% 59.08% 89.20%

2L 81.83% 16.36% 64.28%

3L 75.32% 9.76% 55.93%

DL 80.51% 29.44% 65.75%

CS DS-2 1L 72.73% 52.80% 68.21%

2L 73.28% 54.79% 73.48%

3L 72.46% 53.11% 72.22%

DL 73.31% 55.36% 73.93%

... ... ... ... ... ...

Table 2 was constructed, based on Table 1, verify-

ing on which side each measure had the best perfor-

mance and if this performance occurred in both data

sets (the better’s performances values are indicated in

gray for each of the options). For example, in Table 2,

the Added Value measure had, in both data sets, the

best performance in the rhs. The measures marked

with:

* indicates that in one of the twenty-four options con-

sidered in each measure (twelve for each data set)

shown in Table 1, the side that had the best perfor-

mance with the measure was the lrhs and the side

indicated in Table 2 the second best performance.

** indicates that in two of the twenty-four options

considered in each measure (twelve for each data

set) shown in Table 1, the side that had the best

performance with the measure was the lrhs and

the side indicated in Table 2 the second best per-

formance. However, for the Interest Factor mea-

sure the best performance is related to the rhs.

**/* indicates that in two of the twenty-four options

considered in each measure (twelve for each data

set) shown in Table 1, the side that had the best

performance with the measure was the lrhs and in

one of the options the lrhs draw. In both cases, the

measure indicated in Table 2 had the second best

performance.

The only measure that did not present a pattern

and, therefore, is not found in Table 2, was the J-

Measure. Observe that almost all of the measures of

the rhs presented a pattern (90.91% (10/11)), that is,

this side did not present in any way an exception in re-

lation to the side that had the best performance in one

speciﬁc measure, different from the lhs measures.

Table 2: Grouping of objective measures with respect to the

generalization side performance.

Side lhs rhs

Measure Collective Strength** Added Value

Cosine**/* Certainty Factor

φ-coefﬁcient* Conﬁdence

Jaccard** Conviction

Kappa Gini Index*

Interest Factor** Klosgen

Mutual Information Goodman-Kruskal’s

Piatetsky-Shapiro’s* Laplace

Odds Ratio

Yule’s Q

Yule’s Y

From the results shown in Table 2, we can con-

clude that for each generalized side there is a proper

set of measures that is better for the GAR quality eva-

luation. (Carvalho et al., 2007b) presents a compari-

son between the results presented above with a litera-

ture previous research.

5 CONCLUSION

This work presented an approach, called GARPA, to

obtain a generalized association rules set considering

an existing specialized association rule set obtained

beforehand and taxonomies given by a domain ex-

pert. For each of the obtained generalized rules it

is possible to identify the specialized rules that were

grouped in order to generate the generalized rule and

to know the participation of each specialized item in

the general items. It is important to note that GARPA

is useful when the user wants to post-process a set of

specialized rules through domain knowledge since he

can obtain a more reduced and more expressive set of

ICEIS 2007 - International Conference on Enterprise Information Systems

314

rules to facilitate his comprehension of the extracted

knowledge.

Experiments were carried out in two data sets aim-

ing to evaluate the knowledge quality expressed by

the generalized rules. The analysis showed that de-

pending on the side occurrence of a generalization

item a different group of measures has to be used

to evaluate the GAR quality. In other words, if a

rule presents a generalized item in the lhs, the lhs

measures (Table 2) have to be used, since these mea-

sures have a better behavior when applied to evaluate

a GAR with a generalized item in the lhs; the same

idea applies to the rhs. Thus, this paper gives a huge

contribution to the post-processing knowledge step.

An analytical evaluation of some presented objec-

tive measures is presented in (Carvalho et al., 2007a)

to base the empirical results.

ACKNOWLEDGEMENTS

We wish to thank the Instituto Fbrica do Milnio (IFM)

and Fundao de Amparo Pesquisa do Estado de So

Paulo (FAPESP) for the ﬁnancial support.

REFERENCES

Adamo, J.-M. (2001). Data Mining for Association Rules

and Sequential Patterns. Springer-Verlag.

Agrawal, R. and Srikant, R. (1994). Fast algorithms for

mining association rules. In Bocca, J. B., Jarke, M.,

and Zaniolo, C., editors, Proceedings of the 20th In-

ternational Conference on Very Large Data Bases,

VLDB’94, pages 487–499.

Baixeries, J., Casas, G., and Balc

azar, J. L. (2000). Fre-

quent sets, sequences, and taxonomies: New, efﬁcient

algorithmic proposals. Technical Report LSI-00-78-

R, Departament de LSI – Universitat Polit

ecnica de

Catalunya.

Carvalho, V. O., Rezende, S. O., and Castro, M. (2007a).

An analytical evaluation of objective measures beha-

vior for generalized association rules. In IEEE Sympo-

sium on Computational Intelligence and Data Mining

– CIDM/2007. In Press.

Carvalho, V. O., Rezende, S. O., and Castro, M. (2007b).

Evaluating generalized association rules through ob-

jective measures. In Deved

zic, V., editor, IASTED In-

ternational Conference on Artiﬁcial Intelligence and

Applications – AIA 2007. ACTA Press.

Chung, F. and Lui, C. (2000). A post-analysis frame-

work for mining generalized association rules

with multiple minimum supports. In Post-

Processing in Machine Learning and Data

Mining: Interpretation, Visualization, Inte-

gration, and Related Topics (Workshop within

KDD’2000). Retrivied November 17, 2006, from

http://www.cs.ﬁt.edu/ pkc/kdd2000ws/post.html.

Domingues, M. A. and Rezende, S. O. (2005). Using ta-

xonomies to facilitate the analysis of the association

rules. In Proceedings of ECML/PKDD’05 – The Se-

cond International Workshop on Knowledge Disco-

very and Ontologies (KDO-2005), pages 59–66.

Han, J. and Fu, Y. (1995). Discovery of multiple-level asso-

ciation rules from large databases. In Dayal, U., Gray,

P. M. D., and Nishio, S., editors, Proceedings of 21th

International Conference on Very Large Data Bases

VLDB’95, pages 420–431.

Han, J. and Fu, Y. (1999). Mining multiple-level association

rules in large databases. IEEE Transactions on Know-

ledge and Data Engineering, 11(5):798–805.

Hipp, J., Myka, A., Wirth, R., and G

untzer, U. (1998). A

new algorithm for faster mining of generalized asso-

ciation rules. In Zytkow, J. M. and Quafafou, M., edi-

tors, Proceedings of the 2nd European Symposium on

Principles of Data Mining and Knowledge Discovery

PKDD’98, pages 74–82.

Huang, Y.-F. and Wu, C.-M. (2002). Mining genera-

lized association rules using pruning techniques. In

Proceedings of the 2002 IEEE International Confe-

rence on Data Mining (ICDM’02), pages 227–234,

Washington, DC, USA. IEEE Computer Society.

Srikant, R. and Agrawal, R. (1995). Mining generalized

association rules. In Proceedings of the 21th In-

ternational Conference on Very Large Data Bases

VLDB’95, pages 407–419.

Srikant, R. and Agrawal, R. (1997). Mining generalized

association rules. Future Generation Computer Sys-

tems, 13(2/3):161–180.

Sriphaew, K. and Theeramunkong, T. (2004). Fast algo-

rithms for mining generalized frequent patterns of ge-

neralized association rules. IEICE Transactions on In-

formation and Systems, 87(3):761–770.

Tan, P.-N., Kumar, V., and Srivastava, J. (2004). Selecting

the right objective measure for association analysis.

Information Systems, 29(4):293–313.

Weber, I. (1998). On pruning strategies for discovery

of generalized and quantitative association rules. In

Bing, I. L., Hsu, W., and Ke, W., editors, Proceedings

Knowledge Discovery and Data Mining Workshop

Pricai’98. 8 pp.

Yen, S.-J. and Chen, A. L. P. (2001). A graph-based ap-

proach for discovering various types of association

rules. IEEE Transactions on Knowledge and Data En-

gineering, 13(5):839–845.

OBTAINING AND EVALUATING GENERALIZED ASSOCIATION RULES

315