MAKING INCOMPLETE INFORMATION

VISIBLE IN WORKFLOW SYSTEMS

Georg Peters

Munich University of Applied Sciences

Faculty of Computer Science and Mathematics

Lothstrasse 34, 80637 Munich, Germany

Roger Tagg

University of South Australia, School of Computer and Information Science

Mawson Lakes, SA 5095 Australia

Keywords: Workflow Systems, Process Mining, Partial Information, Soft Computing, Rough Sets.

Abstract: After a bumpy start in the nineties of the last century workflow systems have recently re-gained the focus of

attention. Today they are considered as a crucial part of the recently introduced middleware based ERP

systems. One of the central objectives and hopes for this technology is to make companies more process-

orientated and flexible to keep up with the increasing speed of change of a global economy. This requires

sophisticated instruments to optimally manage workflow systems, e.g. to deal with incomplete information

effectively. In this paper we investigate the potential of rough set theory to make missing or incomplete

information visible in workflow systems.

1 INTRODUCTION

After a breezy start in the nineties of the last century

and a decline soon afterwards, workflow systems are

now considered among the key enablers for

middleware based ERP-systems.

Van der Aalst and van Hee (2002) describe four

phases of information systems: which started with

the initial phase, that of decomposed applications.

Then successively the data and the user interface

management were taken out of the application.

Today, the (business) processes are being taken out

of the applications and are managed in specially

design process management software. Workflow

systems form a key technology in achieving this last

phase.

The main intention with this new approach is to

make a company more flexible and provide it with

better possibilities to adapt to new market

challenges. This has become of increasing

importance since the trend towards a global

economy requires companies to adapt to market

changes quicker than some 20 or 30 years ago.

However, the environment of companies today,

as well as being subject to high degrees of change, is

characterized by insecurity and vagueness. To deal

with vagueness, soft computing (Hoffmann et al.

2005) or granular computing (Bargiela, Pedrycz

2002) concepts provide well accepted methods.

Under these umbrellas fuzzy sets, neutral nets,

genetic algorithms and other techniques are

subsumed to provide a rich toolbox to deal formally

with the vagueness which is immanent in the real

world.

Recently rough set theory (Pawlak 1982) has

gained increasing attention and has established itself

as a concept of soft computing. It is an approach to

better deal with certainty, indiscernibility and similar

situations.

In the meantime rough sets have been rapidly

extended theoretically and many areas of

applications have been suggested. These cover

bioinformatics (e.g. Mitra 2004), pattern recognition

(e.g. Skowron et al. 2001), multi-criteria decision

support (e.g. Slowinski 1993), case-based reasoning

(e.g. Polkowski et al. 1996), concurrent processes

(e.g. Suraj 2000) and many more.

434

Peters G. and Tagg R. (2007).

MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - ISAS, pages 434-440

DOI: 10.5220/0002361804340440

 SciTePress

The objective of this paper is to utilize the

concept of rough sets to make partial or incomplete

information in workflow systems visible, in order to

deal with it more effectively.

The remainder of the paper is organized as

follows. In the next Section we give a short

introduction to rough set theory. In Section 3 we

apply the concept of rough sets to workflow

systems. Section 4 discusses how these ideas might

be offered to process managers and end users. The

paper ends with a short conclusion.

2 ROUGH SETS

2.1 Fundamentals of Rough Set Theory

Since Pawlak introduced rough sets in 1982 (Pawlak

1982, 1992) they have gained increasing importance

and are today considered as a central part of soft

computing and granular computing.

The basic idea of rough set theory is that there

are two kinds of objects. While some objects are

clearly distinguishable from each other some objects

are indiscernible - normally because of missing or

incomplete information.

This has led to the concept of lower and upper

approximations of sets. An object in a lower

approximation of a set surely belongs to the set,

while an object in an upper approximation only may

belong to the corresponding set. Consequently it

cannot be a member of more than one lower

approximation simultaneously. The area of an upper

approximation that is not covered by a lower

approximation is often called a boundary area.

Lower Approximation of a Set

Upper Approximation of a Set

Lower Approximation of a Set

Upper Approximation of a Set

Boundary AreaBoundary Area

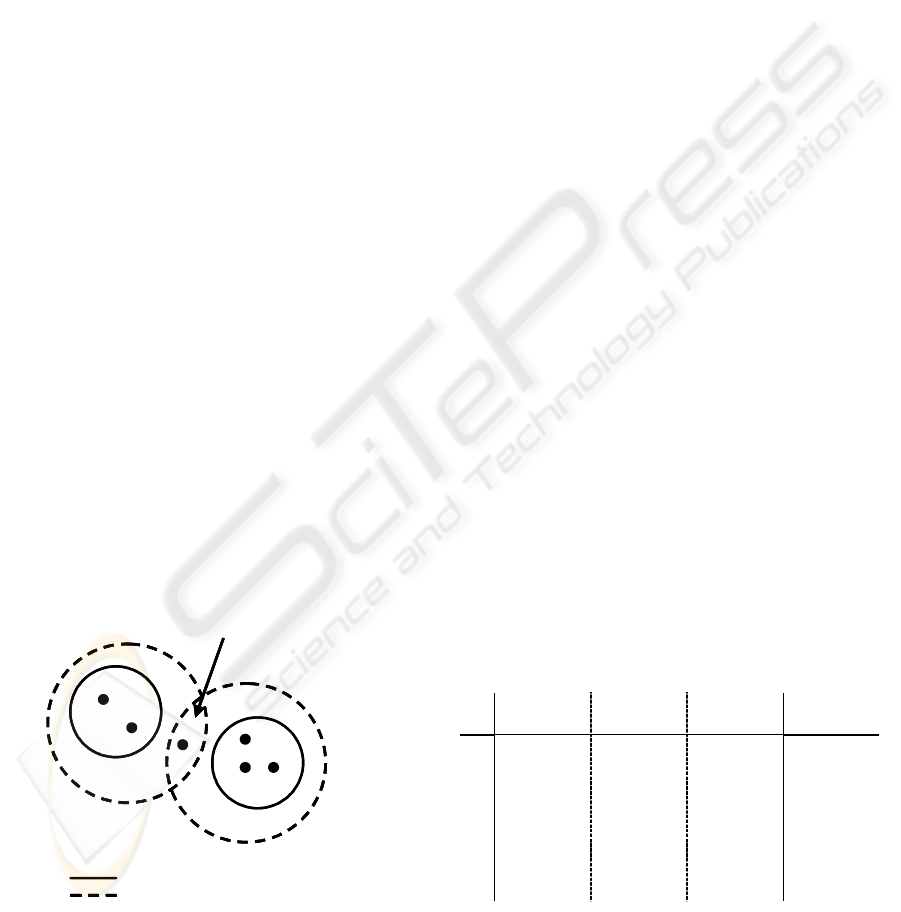
Figure 1: Lower and Upper Approximations.

This leads to the three basic properties of rough

set theory:

1. An object can be a member of one lower

approximation at most.

2. An object that is a member of the lower

approximation of a set is also member of the

upper approximation of the same set.

3. An object that does not belong to any lower

approximation is member of at least two

upper approximations.

In the context of this paper we limit our

presentation of the fundamentals of rough sets to

these three properties. However, rough set theory is

much richer and covers such aspects as certainty

versus coverage, global and local coverage, reducts,

indiscernability relations, minimal complex and

many more. For a basic introduction to rough sets

theory see (Grzymala-Busse, 2004). More detailed

surveys, specially on its mathematical foundations,

can be found for example in (Komorowski. 1999) or

(Polkowski, 2003).

Note that in contrast to fuzzy set theory (Zadeh,

1965; Zimmermann, 2001) where an object belongs

to more than one set simultaneously (indicated by

membership degrees), in rough set theory it is

assumed that an object belongs to one and only one

set. However, due to missing or contradictory

information the actual memberships of the objects in

the boundary areas remain unclear. See e.g. Dubois

and Prade (1990) for a detailed discussion on the

relationship of fuzzy and rough sets.

2.2 An Example for Rough Sets

Consider the following example (Grzymala-Busse

2004) dealing with a decision table of eight patients

showing different symptoms (Table 1). Four of the

patients are well while the remaining four patients

suffer from flu: decision {Flu=yes}.

Table 1: Patient’s Decision Tree.

# Temp-

erature

Headache Nausea Decision:

Flu

1. high yes no yes

2. very_high yes yes yes

3. high no no no

4. high yes yes yes

5. high yes yes no

6. normal yes no no

7. normal no yes no

8. normal yes no yes

Patients #1 and #2 belong to the lower

approximation of the set {Flu=yes} since there are

no conflicts with the diagnoses of the remaining

patients. The same applies to patients #3 and #7.

MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS

435

They belong to the lower approximation of the set

{flu=no}.

This means that patients showing the same

symptoms as patients #1 and #2 can be considered as

ill and patients with the same symptoms of patients

#3 and #7 are without flu.

However with the data shown, a diagnosis is not

possible for patients showing the same symptoms as

patients #4, #5, #6 and #8. There are contradictions

or missing information in this data set.

Patients #4 and #5 have the same symptoms

{high, yes, yes}, however patient #4 suffers from flu

while #5 is well. The same applies to patients #6 and

#8 with the symptoms {normal, yes, no} but

different diagnoses.

2.3 Interval Based Rough Sets

While original rough set theory is purely set-based, a

new interval driven approach has been established in

the meantime (e.g. Yao et al. 1994). Applications of

interval based rough set theory are in the field of

cluster analysis (Lingras et al. 2004, Peters 2006)

and others.

3 ROUGH WORKFLOW

MANAGEMENT

3.1 Rough Petri Nets

Rough Petri nets were introduced by J.K. Peters et

al. (1998, 1999, 2000, 2003).

The central idea of rough Petri nets is to design a

rough guard (soft guard) which determines whether

a transition is enabled or not. Peters et al. discuss the

properties of their rough Petri nets by giving

examples of sensor and filter models.

3.2 Utilizing Rough Sets in Workflow

Management

Many notations for the design of workflows have

been suggested, e.g. eEPC (Scheer 2000), UML

(Fowler 2003) or Petri nets (Murata 1989). The

relationships of these approaches have been

discussed extensively and transformation rules

between them have been suggested (e.g. van der

Aalst 1999; van Hee, 2005).

So, following Peters et al., we will make use of

the Petri net notation to show the potential of rough

set theory for workflow management. The main

reason for choosing this notation lies in the strong

mathematical foundations of Petri nets that make it

easier to integrate rough sets.

However, in contrast to Peters et al., we will

restrict our presentation to the basic idea of rough

sets. We furthermore focus on the “story” and avoid

formal representations as far as possible. Our focus

lies on the detection of incomplete and missing

information in workflow systems rather than in the

design of soft guards.

3.2.1 Patient’s Decision Tree as a Petri Net

Consider again the example given in Section 2.2.

The decision tree can be designed as a simple Petri

net consisting mainly of an (exclusive) OR-construct

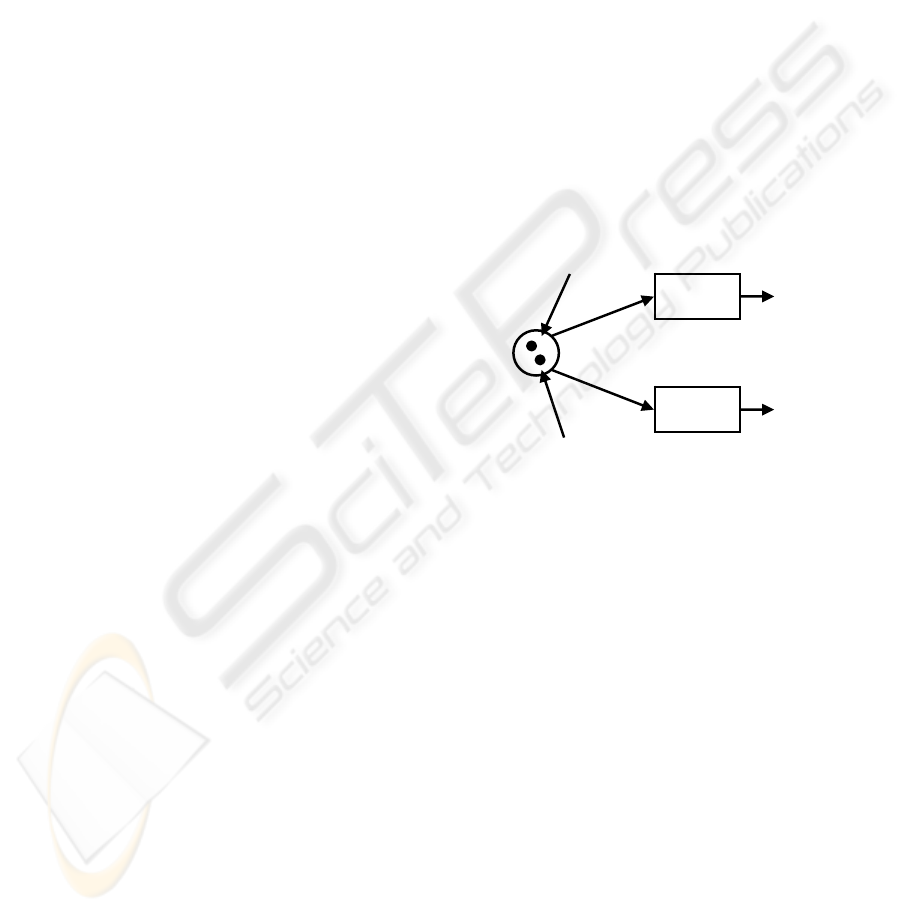
and the patients symbolised as tokens (see Figure 2).

For simplicity we will only display patients #1 and

#2 in

Figure 2.

…

Flu=yes

Flu=no

Patient #1

{high, yes, no}

Patient #2

{very_high, yes, yes}

Figure 2: Patient’s Decision Tree as a Petri Net.

Both of the explicitly displayed patients (#1 and

#2) fulfil the condition {flu=yes} and therefore

continue in branch A of the Petri net for possible

treatments of their illnesses. The same applies to

patients having the same symptoms as #3 and #4.

They continue in branch B of the Petri net where

they possibly return home since they are not ill.

However, the remaining patients with symptoms

equal to #4 and #5 as well as #6 and #8 get stuck

here. On the basis of their symptoms, no decision

can be made as to whether they have flu or not. In

other words, the training set did not provide enough

information to deal with patients having the

symptoms {high, yes, yes} and {normal, yes, no}.

3.2.2 Rough Tokens

Now we can apply rough set terminology to the

situation as described above.

We will distinguish between two views of the

tokens:

ICEIS 2007 - International Conference on Enterprise Information Systems

436

 The local view on a token only considers the

pending decision that means only the next OR-

split.

 Taking the global view we look at the whole

Petri net which means all OR-splits of the net

are considered.

This leads to the following definitions of locally

and globally rough tokens.

3.2.2.1 Locally Rough Tokens

Let us assume that the net as shown in Figure 2 is a

part of a much larger Petri net. So we have a local

view on the two tokens waiting to be routed to

branch A or B of the net.

Since both tokens have attributes that assign

them unambiguously to the set {flu=yes} they

belong to the lower approximation of this set. To

indicate that we only consider the next pending

decision we say that the tokens belong to a local

lower approximation of the Petri net specified by the

place they are occupying and the corresponding

decision {flu=yes}.

Again the same applies to tokens with the

attributes {high, no, no} (according to sample

patient #3) and {normal, no, no} (according to

sample patient #7). Following our arguments given

above they can be assigned to the local lower

approximation of the set {flu=no}.

…

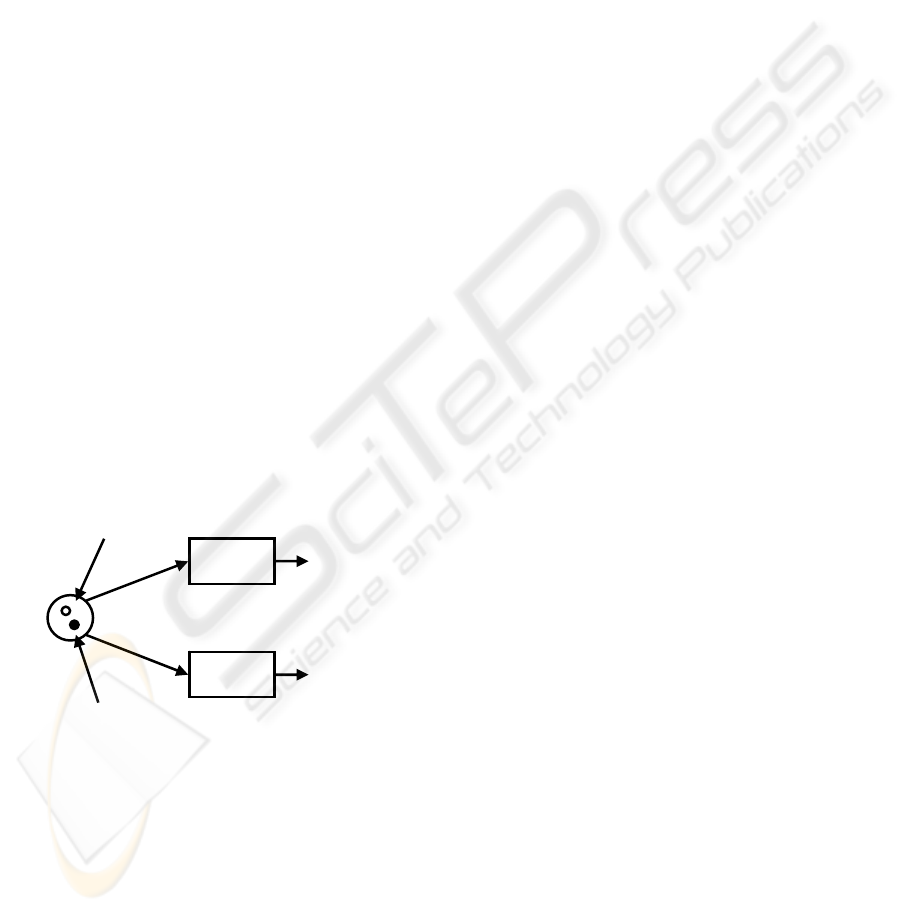
Flu=yes

Flu=no

Token in a local

upper approximation,

e.g. {normal, yes, no}

Token in a local

lower approximation,

e.g. {high, yes, no}

Figure 3: Patient’s Decision Tree as a Petri Net.

Unfortunately patients with the attributes {high,

yes, yes} and {normal, yes, no} cannot be directed

to either branch A or B of the net. They could be ill

or they could be healthy. To indicate this vagueness,

these patients are assigned to the local

approximation of the set {flu=yes} and

simultaneously to the local approximation of the set

{flu=no}. Similarly on the lower approximations we

put the attribute “local” in front of the term “upper

approximation” to indicate the local perspective

limited to one OR-split.

Finally, to graphically distinguish between tokens

(patients) belonging to one local lower or two or

more local upper approximations we suggest their

representation as show in

Figure 3.

The token with the white area in its middle is

stuck at the place, while the completely black token

will be consumed by the transition on branch A.

3.2.2.2 Globally Rough Tokens

Besides the local view that is restricted to one OR-

split, it is also very desirable that a token carries

enough information with it to make it from the start

to the end of a Petri net without the need for

additional information.

Please note, for the sake of simplicity our

formulation is somewhat superficial here. To be

exact a transition consumes tokens from its input

places and produces totally new tokens for its output

places. However this generalization of our concept is

straight forwardly.

Obviously we have the following relationships

between the global and the local views:

 Only tokens that never belong to any local

upper approximation carry sufficient

information to finish the Petri net without the

need for additional external information. To

indicate this we say that they belong to the

global lower approximation of the Petri net (in

contrast to the local lower approximation.

 Any other tokens, i.e. that belong to a local

upper approximation at least one time,

consequently belong to the global upper

approximation (= upper approximation of the

Petri net). These tokens do not have sufficient

internal information to complete the net and

depend on, e.g., external guidance.

So the global view can directly be derived out of

the local view and is an aggregated perspective on

the Petri net.

3.2.3 Rough Places

In the previous section our focus was on the tokens.

In contrast to this we now investigate the role of the

places in respect to the viewpoint of rough

information.

Assume a given number of tokens arrive at an

OR-split. If the decision rule of the OR-split has

MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS

437

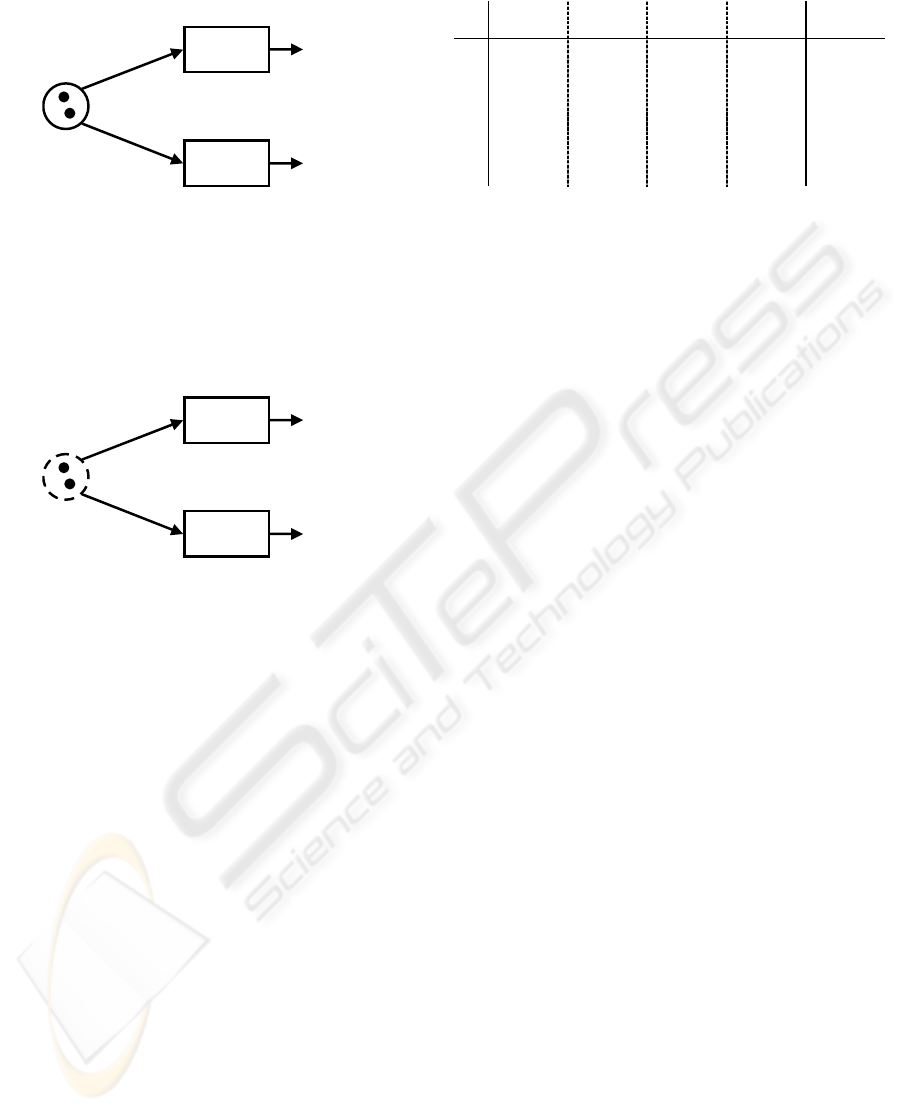
sufficient information to route all tokens, we say that

the input place belongs to the lower approximation.

…

Flu=yes

Flu=no

Figure 4: A Place in a Lower Approximation.

Now, let us consider that a routing decision

cannot be made by the OR-split for at least one

token. In such circumstances we define the input

place as member of an upper approximation. This

indicates that the decision rule of the OR-split is

fragmentary.

…

Flu=yes

Flu=no

Figure 5: A Place in an Upper Approximation.

To graphically distinguish between places

belonging to a lower and upper approximation we

introduce a "dashed circle" place notation as

depicted in

Figure 5 (in contrast to a solid perimeter

as in Figure 4).

Note that this concept can be easily extended to

more general OR-splits, e.g. a three way dispatcher

where one way can be excluded and the remaining

two are possible.

3.2.4 Relationship between Rough Tokens

and Places

On the first sight the relationship between rough

tokens and rough places seems to be fully

symmetric. However consider the extended patient’s

decision table as depicted in Table 2. It now contains

the new attribute dysgeusia.

Table 2: Extended Patient’s Decision Tree.

# Temp-

erature

Head-

ache

Nausea Dysge-

usia

Deci-

sion

1. high yes no yes yes

2. v_high yes yes yes yes

3. high no no no no

4. high yes yes yes yes

5. high yes yes no no

6. normal yes no no no

7. normal no yes no no

8. normal yes no no yes

The decision set is a sub-set of the set of

attributes provided by the patient. Let us consider

the two pairs of patients (#4, #5) and (#6, #8) that

had contradicting information in Table 1.

If we keep the decision set as defined before, the

results remain unchanged. The pairs (#4, #5) and

(#6, #8) are still indiscernible. However since we

only take a sub-set of the possible decision set, we

consider the “problem” as a problem of the place. So

the tokens might be discernible if all attributes are

taken into account.

Actually, the complete decision set delivers an

improved result. The formerly indiscernible patients

(#4, #5) can now be correctly diagnosed with the

additional information (attribute dysgeusia), while

the patients (#6, #8) are still indiscernible.

In summary, the first case would deal with rough

places and the second with rough tokens.

3.2.5 Rough Routes

The analysis of rough routes is a generalization of

global view on the concept of rough places as

discussed in Section 3.2.3.

A route through a net is only determinable when

it consists only of places in lower approximations.

As soon as there is one place in a upper

approximation the route through the net cannot be

determined without any additional information.

Therefore the route gets rough from this place

onwards.

So only for those nets with routes in lower

approximations can one be sure that the tokens

require no additional information to reach the end

place.

ICEIS 2007 - International Conference on Enterprise Information Systems

438

4 POTENTIAL APPLICATION IN

PRACTICE

4.1 Early Warning of Incomplete Case

Information

The main area of application of the proposed method

is to provide early warning of potential delays within

the workflow that could be caused by incomplete

information in certain business cases.

The aim would be to get the workflow system to

alert the end user when a choice is waiting on more

information. In the local case, the next transition will

be held up. In the global case, the alert is a warning

that further down the track, a transition may be held

up.

Ideally, the workflow system should monitor the

arrival of the required extra data, so that transitions

can be automatically enabled without user

intervention. This may well involve facilities to set

up software agents that can talk to the applications

that manage this data.

If, however, it can be seen in advance that certain

combinations of case attributes mean that a choice

cannot be resolved, the workflow template should

probably be altered to allow for a "don't know"

branch. The process owner would need to define

how long cases can be left in this state, and what

should happen to them when time runs out.

4.2 Extending Workflow Models

Workflow management systems mostly depend on a

paradigm in which individual business cases follow

templates that are specified in some description

language similar to a Petri net.

These process modelling tools all depend on a

combination of simple diagrams and property sheets

to capture process templates. They allow the

specification of a number of "case attributes" in their

template property sheets. Attribute values for each

case are provided at run time, either by a human

participant or an associated application.

A combination of case attributes corresponds to

the colour of tokens in the coloured Petri net sense.

The conditions for branching one way or another at a

decision point are expressed as properties of the

outgoing edges of a decision node. If incomplete

information implies that the business case can not

continue, one option would be to introduce a “wait

for data” activity with a loop back to the beginning

of the decision node. However it has to be

acknowledged that adding more complexity in

process model diagrams can be counter-productive.

At run time, some workflow systems offer the

end-user a graphical view of the whole of the current

business case. In Chameleon (O'Hagan, 2005) for

instance, a colour coding of activities in the whole

process is used as follows:

 Pink, activities that are already completed

 Green, activities currently being worked on

 Blue, further activities available to this user

 Yellow, activities not yet available, or not

required.

Although Chameleon models do not strictly

follow Petri net conventions, it would be

theoretically possible to introduce further colour

coding to indicate where incomplete information

threatens to hold up the workflow, either at just the

next decision point or later on, for each business

case.

5 CONCLUSIONS

In this paper we have introduced the fundamental

ideas of rough set theory and showed its potential

use for the management of missing or incomplete

information in workflow systems.

The main purpose is to utilize rough set theory to

make incomplete information visible in order to deal

with such a situation proactively.

Our future research will concentrate on a more

formal incorporation of these concepts into

workflow management.

REFERENCES

Bargiela, A. & Pedrycz, W. (2002), Granular Computing:

An Introduction, Kluwer Acamemic Publishers,

Boston, MA, USA.

Dubois, D. & Prade, H. (1990), 'Rough Fuzzy Sets and

Fuzzy Rough Sets', International Journal of General

Systems 17, 191-209.

Fowler, F. (2003), UML Distilled: A Brief Guide to the

Standard Object Modeling Language, Addison-

Wesley Professional, Boston, MA, USA.

Grzymala-Busse, J. (2004), Introduction to Rough Set

Theory and Applications, in 'KES2004 - 8th

International Conference on Knowledge-Based

Intelligent Information & Engineering Systems'.

Hoffmann, F.; Koeppen, M.; Klawonn, F. & Roy, R., ed.

(2005), Soft Computing: Methodologies and

Applications, Vol. 32, Springer Verlag, Berlin,

Germany.

MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS

439

Komorowski, J.; Pawlak, Z.; Polkowski, L. & Skowron,

A. (1999), Rough Sets: A Tutorial, in S. K. Pal & A.

Skowron, ed., 'Rough-Fuzzy Hybridization: A New

Trend in Decision Making', Springer-Verlag,

Singapore, 3-98.

Lingras, P. & West, C. (2004), 'Interval Set Clustering of

Web Users with Rough K-Means', Journal of

Intelligent Information Systems 23, 5-16.

Mitra, S. (2004), 'An Evolutionary Rough Partitive

Clustering', Pattern Recognition Letters 25, 1439-

1449.

Murata, T. (1989), 'Petri Nets: Properties, Analysis and

Applications', Proceedings of the IEEE 77(4), 541-

580.

O'Hagan, T. (2005), Chameleon Workflow Demos,

University of Queensland website,

http://www.itee.uq.edu.au/~tohagan/Chameleon/

Pawlak, Z. (1982), 'Rough Sets', International Journal of

Information and Computer Sciences 11, 145-172.

Pawlak, Z. (1992), Rough Sets: Theoretical Aspects of

Reasoning about Data, Kluwer Academic Publishers,

Boston, MA, USA.

Peters, G. (2006), 'Some Comments on Rough Clustering',

Pattern Recognition 39(8), 1481-1491.

Peters, J.F.; Skowron, A.; Suraj, Z. & Ramanna, S. (1999),

Guarded transitions in rough Petri nets, in 'Proceed.

EUFIT99 - 7th European Congress on Intelligent

Systems & Soft Computing'.

Peters, J.F.; Skowron, A.; Suraj, Z.; Ramanna, S. &

Paryzek, A. (1998), Modeling real-time decision-

making systems with rough fuzzy Petri nets, in

'Proceed. EUFIT98 - 6th European Congress on

Intelligent Techniques & Soft Computing', pp. 985-

989.

Peters, J.F.; Ramanna, S.; Suraj, Z. & Borkowski, M.

(2003), Rough Neurons: Petri Net Models and

Applications., in A. Skowron S.K. Pal, L. Polkowski,

ed.,' Rough-Neuro Computing', 472-491.

Peters, J.F.; Skowron, A.; Suray, Z. & Ramanna, S.

(2000), Sensor and Filter Models with Rough Petri

Nets, in H.D. Burkhard; L. Czaja; A. Skowron & P.

Starke, ed., 'Proceedings of the Workhop on

Concurrency, Specification and Programming',

Humboldt-University, Berlin, 203-211.

Polkowski, L.; Skowron, A. & Komorowski, J. (1996),

Approximate case-based reasoning: A rough

mereological approach, in 'Proceed. 4-th German

Workshop on Case Based Reasoning, System

Developments and Evaluation', pp. 144-151.

Polkowski, L. (2003), Rough Sets, Physica-Verlag,

Heidelberg, Germany.

Scheer, A. (2000), ARIS - Business Process Modeling,

Springer-Verlag, Berlin, Germany.

Skowron, A. & Swiniarski, R. (2001), Rough Sets in

Pattern Recognition, in Pal, S.K. and Pal, A., Pattern

Recognition: From Classical to Modern Approaches,

World Scientific, Singapore, pp. 385-425.

Slowinski, R. (1993), Rough set learning of preferential

attitude in multi-criteria decision making, in J.

Komorowski & Z. Ras, ed., 'Methodologies for

Intelligent Systems', Springer-Verlag, Berlin,

Germany, pp. 642-651.

Suraj, Z. (2000), Rough set methods for the synthesis and

analysis of concurrent processes, in Polkowski, L. and

Tsumoto, S. and Lin, T., Rough set methods and

applications: new developments in knowledge

discovery in information systems, Physica-Verlag,

Heidelberg, Germany, pp. 379-488.

van der Aalst, W. & van Hee, K. (2002), Workflow

Management - Models, Methods, and Systems, MIT

Press, Cambridge, MA, USA.

van der Aalst, W. (1999), 'Formalization and Verification

of Event-driven Process Chains', Information and

Software Technology 41(10), 639-650.

van Hee, K.; Oanea, O. & Sidorova, N. (2005), Colored

Petri Nets to Verify Extended Event-Driven Process

Chains, in ' Proceed. CoopIS 2005 - 13th International

Conference on Cooperative Information Systems', pp.

183-201.

Yao, Y.; Li, X.; Lin, T. & Liu, Q. (1994), Representation

and Classification of Rough Set Models, in

'Proceedings Third International Workshop on Rough

Sets and Soft Computing', pp. 630-637.

Zadeh, L. (1965), 'Fuzzy Sets', Information and Control 8,

338-353.

Zimmermann, H. (2001), Fuzzy Set Theory and its

Applications, Kluwer Academic Publishers, Boston,

MA, USA.

ICEIS 2007 - International Conference on Enterprise Information Systems

440