INTEGRATION OF A FUZZY SYSTEM AND AN INFORMATION

SYSTEM FOR THE TERRITORIAL UNITS RANKING

Miroslav Hudec

Institute of Informatics and Statistics, Dubravska cesta 3, Bratislava, Slovakia

Mirko Vujošević

Faculty of Organizational Sciences, University in Beograd, Beograd, Serbia

Keywords: Fuzzy systems, ranking, territorial unit, information system.

Abstract: For ranking and classification of the territorial units, up-to-date and precise data as well as ranking tool are

needed. The advantage of fuzzy systems (FS) in these tasks is in definition of a problem by linguistic terms.

The disadvantage is in universality and complexity of the fuzzy systems for end users. This disadvantage

comes from usage of FS to solve a wide area of different tasks. The advantages and the disadvantages, as

well as constraints of FS are analyzed. The aim of this paper is to show the information systems about

territorial units of the Slovak Republic and possibilities of integration fuzzy system for ranking territorial

units with these information systems. This approach enables creation of the model, importing the input data,

processing of the rules and presentation of the solution in a usable and understandable form. In this case

solution is presented on a thematic map too.

1 INTRODUCTION

The elements of significant importance for the

ranking and classification of the territorial units are

adequate number of indicators, their precise and up-

to-date collection and qualitative usage of data for

ranking. The support for ranking can be attained

only with the design and implementation of an

accurate information system and an adequate system

for the territorial units ranking.

The aim of the research presented in this paper is

to illustrate how this amount of data and FS can be

used in classification and ranking problems. The

classification and ranking of the territorial units is of

significant importance for the regional development

planning. The paper aims to present abilities of FS

as an alternative approach to classical statistical

methods for the classification and ranking tasks.

The collection and storage of data, even if exist a

prefect information system for collect all possible

indicators for all territorial levels, is an excellent

basis but without reference to usage them in research

and decision process is unuseful.

This paper briefly describes information systems

for territorial units in the Slovak Republic. This

paper also discusses some advantages and

disadvantages of the fuzzy approach for the

territorial units ranking and suggests the integrated

FS (IFS) with statistical information systems.

2 INFORMATION SYSTEMS FOR

TERITORIAL UNITS

The MOŠ/MIS (Urban and municipality statistics/

Urban information system) is officially used in the

Statistical Office of the Slovak Republic. The

INFOREG (Information system for support of the

regional development) is in the phase of pilot

application. The data from these two systems can be

used for ranking of territorial units.

The MOŠ/MIS is developed according to the

Nomenclature of Units for Territorial Statistics

(NUTS) which defines hierarchical and geographical

dividing of territory in a country. NUTS

classification is important in the harmonization and

comparing of regional data between countries that

have implemented NUTS. All territorial units at the

first three levels of NUTS have unique code in

374

Hudec M. and Vujoševi

c M. (2007).

INTEGRATION OF A FUZZY SYSTEM AND AN INFORMATION SYSTEM FOR THE TERRITORIAL UNITS RANKING.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 374-377

DOI: 10.5220/0002355103740377

 SciTePress

whole EU. The basic territorial units for the

MOŠ/MIS are urbans and municipalities on level 5

of NUTS. This system covers collection of

indicators for this level only. This system turned out

to be successful in the municipality statistical area.

The INFOREG platform facilitates data

collection, storage, management of data and their

presentation for all NUTS levels. The structure of

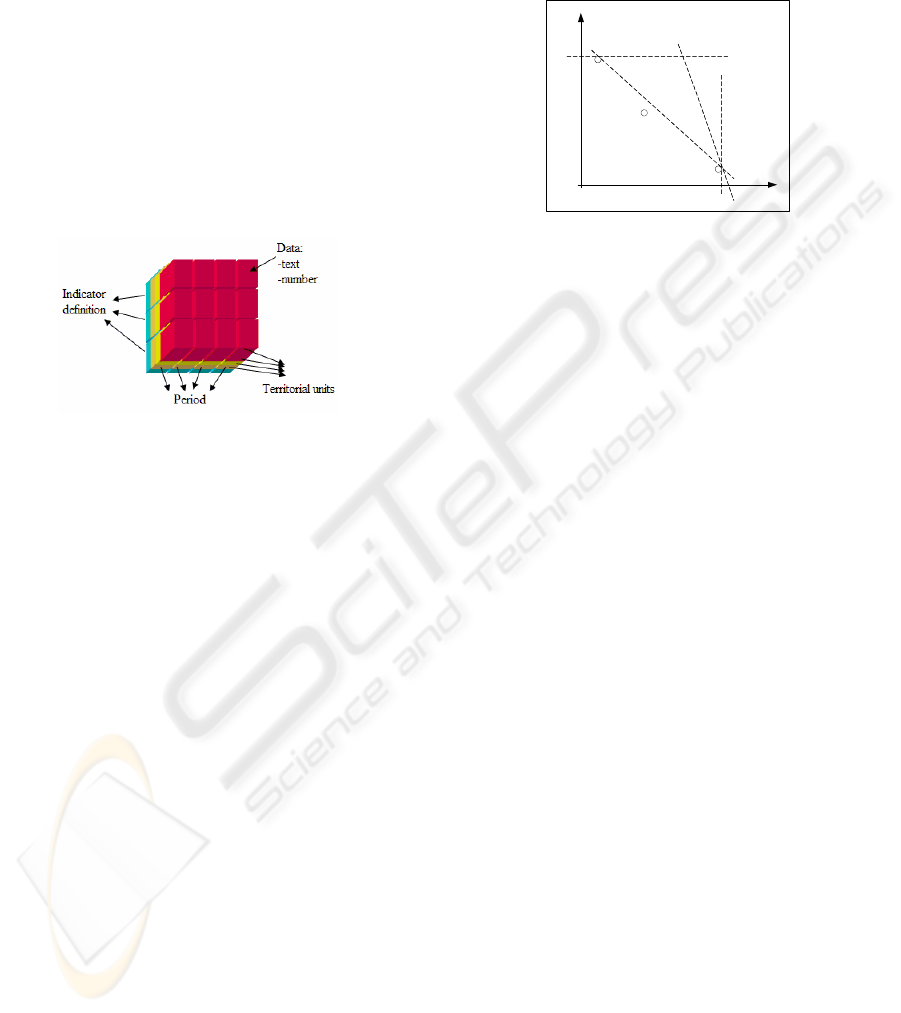
the INFOREG database consists of these

dimensions: indicator, territorial unit and period.

The structure of database is presented in three-

dimensional cube in figure 1 (Priehradníková,

Benčič and Hudec, 2005). In the intersection of

dimensions is the indicator value. For example: 70

inhabitants/km

is density of population (source

Statistical Office) for Bystrica region for 2003 year.

Figure 1: Structure of three-dimensional cube.

The territorial unit dimension is defined by

NUTS classification. The period presents all

possible periods of collecting indicator values. The

dimension of indicator has the most complex

requirements. The set of indicators is vast and there

is the expectation that new indicators might be

added according to requirements for information.

The main qualitative impacts of INFOREG are:

• effective support for research and

development, strategy building, realization

of the regional policy and investments during

their decision making processes;

• development of sophisticated indicators

system, which reflects the situation in

municipalities and regions.

The next chapters present the FS use in ranking

and classification tasks and the development of the

integrated FS with the information systems

mentioned above.

3 FUZZY APPROACH

The process of finding the best solution or ranking

of the objects could be done using different methods.

Classical methods usually use ponders to set

importance for each attribute. Figure 2 shows

situation when a system based on logic (an expert

system) allows to obtain expected solution (point C)

whereas by the method based on ponders is not

possible to reach this solution. Depending of the

changes in coefficient values for attributes X

and X

the object function f reaches solutions A or B.

Figure 2: Finding of the best solution.

If is classical expert system widened with the

fuzzy logic, fuzzy expert system or just fuzzy system

based on the fuzzy “if-then” rules is attained. FS

includes fuzzy sets and fuzzy logic into inference

process and that gives significant advantages beyond

the constraints of classical logic in many different

tasks. The fuzzy logic possesses the ability to mimic

the human mind to effectively calculate modes of

reasoning that are approximate.

3.1 Advantages and Disadvantages

Despite the fact of important results in practical

applications, fuzzy approach is not a total

generalization of the Boolean algebra (BA) for the

multivalued logic (Radojević, 2005). It means that

the fuzzy approach is not capable to fulfill some of

the axioms or theorems of BA. For example the sum

of atomic functions

), , , (

____

babababa ∧∧∧∧

is not

always equal to 1 and the excluded middle

)(

aa ∨

and the contradiction

)(

aa ∧

laws are not satisfied

always. According to these, it can be considered that

fuzzy algebra: <[0,1], T, S, N> where T denotes T-

norm, S is S-norm and N is complement, is not BA.

It is possible to avoid these disadvantages and to

exploit good properties of fuzzy approach by

analysis of each task to keep staying in BA frame.

In case of using

) ( ba ∧

rule, the min T-norm

gives good output solution. Lukasiewicz T-norm

gives more restricted output when membership

degrees of a and b satisfy relation (a+b)<1, because

the consequence of rule is always equal to zero. The

advantage of Lukasiewicz T-norm is in the event of

using complement in rules:

)(

ba ∧

and when some

of controlling rules, like contradiction

)(

aa ∧

are

used. In these cases Lukasiewicz T-norm satisfy

Boolean axiom whereas min T-norm does not satisfy

it. In case of softly ranking of municipalities by min

INTEGRATION OF A FUZZY SYSTEM AND AN INFORMATION SYSTEM FOR THE TERRITORIAL UNITS

RANKING

375

T-norm all municipalities that have sum of all

membership functions in rule less than 1 can be

ranked. If FS uses for example aggregation

) ( ba∧

and if min T-norm is used, what is usual case in real

applications then FS is consistent with the BA.

If restrictions mentioned above are satisfied, the

FS can be suscessfuly used in ranking and

classification tasks because they:

• enables the creation of logical inference

system based on human mind including

uncertainities in membership degrees to the

appropriate fuzzy sets.

• supports the inference process based on “IF-

THEN” rules.

• enables accessible and understantable

knowledge base for users.

The Sugeno model of fuzzy inference system

(FIS) from the MatLab software is implemented for

municipalities ranking according to needs for the

road maintenance in winter. The data from the

MOŠ/MIS were used. (Hudec and Vujošević, 2005).

The disadvantage is in the complexity of using

FIS in software products (MatLab…) and non-

existence of integration between FIS and databases

for domain experts. The decision makers

requirement for FIS is its simplicity for use to

impose the obvious advantages of the FS. The FIS

usually does not satisfy this criteria. The powerful

software for FIS is produced for wide area of tasks

and is complicated for users. In order to solve a task,

the decision maker needs the assistance from an

information system expert for preparing the input

data from database into proper format for FIS and

for presenting results in useful form. The decision

maker also needs an operational research expert to

set appropriate functions for aggregation,

implication, accumulation and defuzzification in

FIS. The FIS tools usualy offer variety of functions

and fuzzy model could become unreliable if

unparopriate functions are chosen.

3.2 Integrated Fuzzy System

The Integrated fuzzy system (IFS) was developed to

avoid disadvantages mentioned above. Figure 3

shows the IFS for territorial units ranking. The

interface to database enables the selection of

territorial units and indicators which are important

for ranking task. Selected territorial units and values

of chosen indicators are converted into appropriate

matrix form for the FIS.

In suggested IFS the zero ordered Sugeno model

of fuzzy inference is used. Unconditional fuzzy rules

are not of interest in territorial ranking tasks so to

use Mamdani model is not necessary. FIS can be

expanded in future by Mamdani model to use non

singleton fuzzy sets in the model output part.

Ordinary fuzzy sets as triangular, trapezoidal or

bell shaped type are used in the IFS. These fuzzy

sets are not complicated and in this case keep

enough information for description of ambiguity

from the decision maker point of view. The next step

is the knowledge representation using inference

rules that connect the input with the output. The

rules are of the “if-then” form. Although

determining of these rules is intuitive, it is very

important to include all interesting cases in these

rules. Antecedent part of the rule is connected by

and, or or not operators. The fuzzy model for a

ranking task is after these two steps defined. The

next step is the processing of the rules for selected

territorial units. Processing of the rules depends on

selected functions for aggregation, implication and

accumulation. Min T-norm is used for “and“

aggregation. In order to support selection of proper

T-norm for fuzzy model defined by user, integrated

system would have to select appropriate T-norm

according to selected type of fuzzy rules. For the

implication, the Mamadani implication is used.

In order to solve a ranking problem within a

knowledge-based fuzzy system it is necessary to

provide results in a usable and understandable form.

The result of ranking in a vector form is connected

with code list of territorial units and exported into

xls format for additional spreadsheet calculations. In

territorial units ranking, providing the result in a

thematic map is very useful too. For this purpose the

result form the FIS is adapted for presenting results

in a map. The rank for every territorial unit, obtained

by the FIS and determined by territorial unit primary

key, is connected across this key to the identification

of the particular polynomial area of the vector map.

The map shows territorial survey of municipality

ranking. These two modes for presenting of the

results are shown in the right part of Figure 3.

The FIS is under development in the VB.NET as

well as other parts of IFS: the database interface and

the export solutions to the spreadsheet calculations

format and maps. The knowledge and experiences

obtained from ranking of municipalities by existing

FIS in the MatLab was used for IFS development.

More comparison to the other systems for

estimation and ranking (e.g. DEA, or OLAP) will be

done once the IFS is implemented. This comparison

is interested in the obtained result as well as in

ICEIS 2007 - International Conference on Enterprise Information Systems

376

Figure 3: Integrated fuzzy system.

simplicity of use for end users. The second

comparison means level of satisfaction of the system

functionality for easiest creation of a model and for

solving particular ranking task from decision maker

point of view.

The IFS can be used in ranking tasks for

territorial units in other countries too. This

possibility is at this moment only theoretical. There

are some more conditions that have to be satisfied.

Hierarchical structures of territorial units in

databases need to be compatible with the NUTS and

adequate maps for territorial units need to be

available for use.

4 CONCLUSIONS

The support for the ranking can be attained only

with the design and implementation of an adequate

information system and an adequate system for

territorial units ranking.

The object of this research was to improve the

support for decision makers during their work with

the statistical data. In this area of work expressions

like: low or high rate of unemployment, low

pollution, etc. are frequently used. It was needed to

adapt and include these expressions into inference

process. Upon the obtained results from previous

research in fuzzy ranking the IFS is suggested as a

support tool for these decision makers.

It was proven in the previous research that the FS

may be successfully used for municipalities ranking

tasks. The results were reasonable and expected

(Hudec and Vujošević, 2005). Disadvantages of the

FS were found too. The aim of this paper was to

avoid some of disadvantages and to exploit

advantages mentioned above. Meanwhile, the

INFOREG was developed. The possibility of the FS

integration with the INFOREG enables more

flexible using of the FS in territorial ranking tasks.

Briefly, the use of the FS has given satisfactory

solutions and the IFS provides better working

environment.

Decision makers and domain experts obtain

useful tool for their work. This tool exempts them

from the help of information and fuzzy systems

experts during preparing of a fuzzy model and the

process solution.

REFERENCES

Benčič A., Hudec M., 2002. MOŠ/MIS–Urban and

municipal statistics project and information system of

the Slovak Republic. SYM-OP-IS’02. Vuletic Print.

Belgrade.

Cox E., 2005. Fuzzy modeling and genetic algorithms for

data mininig and exploration, Morgan Kaufmann

Publishers. San Francisco.

Ioannidis C., Hazichristos T. (2000). A municipality

selection proposal for the expansion of the Hellenic

cadastre using fuzzy logic. Spatial information

management, experience and visions for the 21st

century. Retrived 2004, from

http://www.fig.net/com_3_athens/

Gorzylcany M., 2002. Computational intelligence systems

and applications. Physica Verlag. Heidelberg.

Hudec M., Vujošević M., 2005. Fuzzy systems and neuro-

fuzzy systems for the municipalities classification,

EUROFUSE, 2005, Eurofuse anniversary workshop

on “Fuzzy for Better”.M. Pupin Institute. Belgrade.

Klir G., Yuan B., 1995. Fuzzy sets and fuzzy logic, theory

and applications, Prentice Hall. New Jersey.

Kraliková A., 2001. Regional statistics in the Slovak

Republic, Statistical Office of the Slovak Republic.

Bratislava.

Priehradníková L., Benčič A., Hudec M. (2005, April 21).

Information system for support of regional

development (INFOREG) in the Slovak republic. Joint

ECE/Eurostat/OECD Meeting on the Management of

Statistical Information Systems (MSIS). Retrived May

10, 2004, from http://www.unece.org/stats/

documents/ces/ac.71/2005/18.e.pdf

Radojević D., 2005. Interpolative Relations and

Interpolative Preference Structures. Yugoslav Journal

of Operational Research, YUJOR. Belgrade, Vol. 15,

No 2.. Faculty of organizational Science, Beograd.

INTEGRATION OF A FUZZY SYSTEM AND AN INFORMATION SYSTEM FOR THE TERRITORIAL UNITS

RANKING

377