OPTIMAL ENERGY ALLOCATION FOR DETECTION IN WIRLESS
SENSOR NETWORKS
Krishna Gunturu and Mort Naraghi-Pour
Dept. of Electrical and Computer Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
Keywords:
Hypothesis Testing, Distance measure, Lagrange multiplier.
Abstract:
The problem of binary hypothesis testing in a wireless sensor network is studies in the presence of noisy
channels and for non-identical sensors. We have devised an energy allocation scheme for individual sensors
in order to optimize a cost function with a constraint on the total network energy. Two cost functions were
considered; the probability of error and the J-divergence distance measure. We have also designed a mathe-
matically tractable fusion rule for which optimal energy allocation can be achieved. Results of optimal energy
allocation and the resulting probability of error are presented for different sensor network configurations.
1 INTRODUCTION
In recent years wireless sensor networks (WSN) have
attracted a great deal of attention from the research
community. Typical applications of WSNs include
environmental monitoring, surveillance, intruder de-
tection and denial of access, target tracking, and struc-
ture monitoring, among others. Wireless sensor net-
works can also serve as the first line of detection for
various types of hazards, such as toxic gas or radia-
tion.
The nodes in wireless sensor networks are pow-
ered by batteries for which replacement, if at all pos-
sible, is very difficult and expensive. Thus in many
scenarios, wireless sensor nodes are expected to oper-
ate without battery replacement for many years. Con-
sequently , constraining the energy consumption in
the nodes is a very important design consideration.
In (Luo and Giannakis, 2004), the authors consider
quantization of sensor data and energy allocation for
the purpose of estimation under a total energy con-
straint. Optimal modulation with minimum energy
requirements to transmit a given number of bits with
a prescribed bit error rate (BER) is considered in (Cui
et al., 2005).
In this paper we consider the problem of binary
hypothesis testing using wireless sensor networks un-
der energy constraint. Traditionally, the decentral-
ized detection problem has been investigated assum-
ing identical sensor nodes. For example the work re-
ported in (Zhang et al., 2002; Tsitsiklis, 1988; Varsh-
ney, 1997), considers identically distributed observa-
tions for all the sensor nodes and error-free transmis-
sions from the nodes to the fusion center. In this
paper we do not assume identically distributed ob-
servations. In particular the observation noise expe-
rienced by each sensor may be different. Further-
more, the wireless channels between the sensor nodes
and the fusion center is assumed to be a noisy chan-
nel. Specifically, it is assumed that the nodes’ deci-
sion is transmitted using a modulation scheme over
an AWGN channel. Our goal is to design a fusion
rule and an energy allocation for the nodes so as to
minimize a cost function subject to a limit on the total
energy of all the nodes. We consider two types of cost
functions. The probability of error at the fusion center
as well as the divergence distance measure.
The remainder of this paper is organized as fol-
lows. In Section 2 we present the system model. The
problem of energy allocation for the probability of er-
ror and the J-divergence cost functions is studied in
Sections 3 and 4, respectively. The results are pre-
sented in Section 5 and the conclusions are drawn in
Section 6.
17
Gunturu K. and Naraghi-Pour M. (2007).
OPTIMAL ENERGY ALLOCATION FOR DETECTION IN WIRLESS SENSOR NETWORKS.
In Proceedings of the Second International Conference on Wireless Information Networks and Systems, pages 17-21
DOI: 10.5220/0002150200170021
Copyright
c
 SciTePress

2 SYSTEM MODEL
Let H be a binary random variable with prior prob-
ability distribution given by P(H = H
0
) = q
0
and
P(H = H
1
) = q
1
. We consider a network of n wire-
less sensors with sensor k acquiring a measurement
X
k
about the state of H. Gaussian observations are as-
sumed although the results can be extended to other
cases. With this assumption we have
p
X
k
(x|H
0
) ∼
N (0,σ
2
k
)
p
X
k
(x|H
1
) ∼
N (d,σ
2
k
) (1)
Sensor k computes a local binary decision u
k
ac-
cording to
u
k
=



1, if ln(
p
X
k
(x|H
1
)
p
X
k
(x|H
0
)
) ≥ λ
k
0, if ln(
p
X
k
(x|H
1
)
p
X
k
(x|H
0
)
) < λ
k
For the given distribution in (1) the optimal value
of λ
k
is given by
λ
k
=
d
2
+ σ
k
2
(q
0
−q
1
)
2d
(2)
The channel between sensor k and the fusion cen-
ter is modeled by a binary symmetric channel with
cross over probability ε
k
. The value of u
k
is trans-
mitted to the fusion center over this channel and z
k
denotes the received bit. Let E
T
denote the total en-
ergy available to all the sensors. The fraction of en-
ergy allocated to sensor k is given by x
k
E
T
where
0 ≤x
k
≤ 1 and
∑
n
i=1
x
i
= 1. For the sake of concrete-
ness we assume that the sensors use a BPSK modu-
lation scheme. The value of ε
k
is then given by ε
k
=
Q(
p
2E
T
x
k
/N
0
) where Q(x) =
1
√
2π
∞
x
e
−x
2
/2
dx.
3 ERROR PROBABILITY
CRITERION
The fusion center receives the sequence z =
(z
1
,z
2
,··· , z
n
) and must decide on the state of H.
Finding the optimum decision rule for H based on z is
mathematically intractable. We therefore choose the
following fusion rule.
ψ(z) =

H
1
,
∑
n
i=1
α
i
z
i
≥ τ
H
0
,
∑
n
i=1
α
i
z
i
< τ
(3)
Our motivation here is that for α
i
=
1
σ
2
i
, i = 1, 2,··· ,n,
this is the optimal rule if the fusion center had ac-
cess to the observations {X
k
}. Our goal is to choose
the values of α
i
,x
i
,i = 1,2,··· ,n, and τ such that the
probability or error is minimized subject to the con-
straint that the total energy of the sensor network for
a single measurement and transmission does not ex-
ceed E
T
.
Evaluation of the performance of this rule requires
the distribution of Z =
∑
α
i
z
i
. We invoke the central
limit theorem and assume that, given either hypothe-
sis, Z is a Gaussian random variable (Eremin, 1999).
The conditional moments of Z are then evaluated as
follows.
E(Z|H
ℓ
) =
∑
α
i
E(z
i
|H
ℓ
), ℓ = 0,1 (4)
and
var(Z|H
ℓ
) =
∑
α
i
var(z
i
|H
ℓ
), ℓ = 0,1 (5)
Now
E(z
i
|H
0
) = P(z
i
= 1|H
0
)
= P(z
i
= 1|u
i
= 0, H
0
)P(u
i
= 0|H
0
)
+P(z
i
= 1|u
i
= 1, H
0
)P(u
i
= 1|H
0
)
= ε
i

1−Q

λ
i
σ
i
d
+
d
2σ
i

+(1−ε
i
)Q

λ
i
σ
i
d
+
d
2σ
i

(6)
where ε
i
= Q(
p
2E
T
x
i
/No) is the crossover probabil-
ity for the ith channel. Let E(z
i
|H
0
) = ω
i0
. Then
var(z
i
|H
0
) = ω
i0
(1−ω
i0
) (7)
Similarly for hypothesis H
1
, we have
E(z
i
|H
1
) = P(z
i
= 1|H
1
)
= ε
i

1−Q

λ
i
σ
i
d
−
d
2σ
i

+(1−ε
i
)Q

λ
i
σ
i
d
−
d
2σ
i

(8)
Let E(z
i
|H
1
) = ω
i1
. Then
var(z
i
|H
1
) = ω
i1
(1−ω
i1
) (9)
Let var(z
i
|H
ℓ
) = γ
iℓ
2
. The probability of false
alarm is now given by
P
f
= P(Z ≥ τ|H
0
) = Q
τ−
∑
n
i=1
α
i
ω
i0
p
∑
n
i=1
α
i
2
γ
i0
2
!
(10)
and the probability of detection is given by
P
d
= P(Z ≥ τ|H
1
) = Q
τ−
∑
n
i=1
α
i
ω
i1
p
∑
n
i=1
α
i
2
γ
i1
2
!
(11)
Finally the probability of error is given by
P
e
= q
0
P
f
+ q
1
(1−P
d
) (12)
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
18

Let x = (x
1
,x
2
,··· , x
n
) and y = (α
1
,α
2
,··· , α
n
).
Under the probability of error criteria, we can formu-
late the following optimization problem.
Minimize P
e
(τ,x, y)
Subject to
∑
x
i
= 1
x
i
≥ 0
(13)
Now the Lagrangian is given by
L(τ,x, y,{κ
i
},µ) =
P
e
(τ,x, y) +
n
∑
i=1
κ
i
x
i
+ µ(
n
∑
i=1
x
i
−1) (14)
The Karush-kuhn-Tucker(KKT) (Boyd and Van-
denberghe, 2004) conditions dictate that there must
exist {κ
i
}
n
i=1
and µ such that
x
i
≥ 0, γ
i
≥ 0, κ
i
x
i
= 0, i = 1,2, ..,n. (15)
n
∑
i=1
x
i
= 1 (16)
∇P
e
(τ,x, y) + ∇
n
∑
i=1
κ
i
x
i
+ ∇µ(
n
∑
i=1
x
i
−1) = 0 (17)
where ∇ denotes gradient. By solving this problem
we can obtain the optimal energy allocation x, and
the decision rule (τ,y).
4 DISTANCE MEASURE
CRITERION
In general we would like to perform the energy alloca-
tion using the probability of error as the cost function.
However, as noted in the previous section obtaining
the optimal detection rule may be intractable. In ad-
dition, while currently we are only considering a one
bit quantization of the sensor observations, we would
like to extend our results allowing the sensors to use
more generalized quantizers. In this case obtaining an
expression for the error probability that is suitable for
energy allocation is difficult. Therefore, in this sec-
tion we opt for an alternative cost function, namely
the J-divergence distance measure which belongs to
the class of Ali-Silvey distance measures between
probability measures. Theorems relating the maxi-
mum distance to the minimum probability of error
justify the application of distance measures in our set-
ting (Poor and Thomas, 1977). A lower bound for the
error probability in terms of the J-divergence distance
measure is given in (Kailath, 1967). For more discus-
sion on the Ali-Silvey class of distance measures and
their application for the design of generalized quan-
tizer we refer the reader to (Poor and Thomas, 1977).
The J-divergence distance measure is given by
J(x) = E
H
1
[T(z)] −E
H
0
[T(z)] (18)
where T(z) is the log-likelihood ratio function given
by ln
p(z|H
1
)
p(z|H
0
)
and E
H
ℓ
is expectation operation under
the hypothesis H
ℓ
. We can write
T(z) = ln
p(z|H
1
)
p(z|H
0
)
=
n
∑
i=1
ln
p(z
i
|H
1
)
p(z
i
|H
0
)
(19)
Thus J(x) =
∑
n
i=1
j(x
i
), where
j(x
i
) = (ω
i1
−ω
i0
)ln
ω
i1
ω
i0
+ (ν
i1
−ν
i0
)ln
ν
i1
ν
i0
and where ν
iℓ
= P(z
i
= 0|H
ℓ
) = 1−ω
iℓ
, for ℓ = 0,1.
The optimization problem is now formulated as
follows.
Maximize
n
∑
i=1
j(x
i
) (20)
Subject to
n
∑
i=1
x
i
= 1 (21)
x
i
≥ 0 (22)
The Lagrangian is given by
L(x,{κ
i
},µ) = −
n
∑
i=1
J(x
i
) +
n
∑
i=1
κ
i
x
i
+ µ(
∑
x
i
−1)
(23)
The KKT conditions dictate that there must exist
{κ}
n
i=1
and µ such that:
x
1
≥ 0, κ
i
≥ 0, κx
i
= 0, i = 1,2, ....,n
n
∑
i=1
x
i
= 0
−∇(
n
∑
i=1
J(x
i
)) + ∇(
n
∑
i=1
κ
i
x
i
) + ∇(µ(
n
∑
i=1
x
i
−1)) = 0
(24)
By solving this problem we can obtain the opti-
mal energy allocation x. In this case the fusion rule is
given by
ψ(z) =



H
1
, T(z) > τ
P(H
1
) = a, T(z) = τ
H
0
, T(z) < τ
(25)
where H
1
is chosen with probability a when T(z) = τ.
5 NUMERICAL RESULTS
5.1 Error-Free Channels
To show the efficacy of the prediction rule in (3), we
consider the case of error free channels. The WSN is
OPTIMAL ENERGY ALLOCATION FOR DETECTION IN WIRELESS SENSOR NETWORKS
19

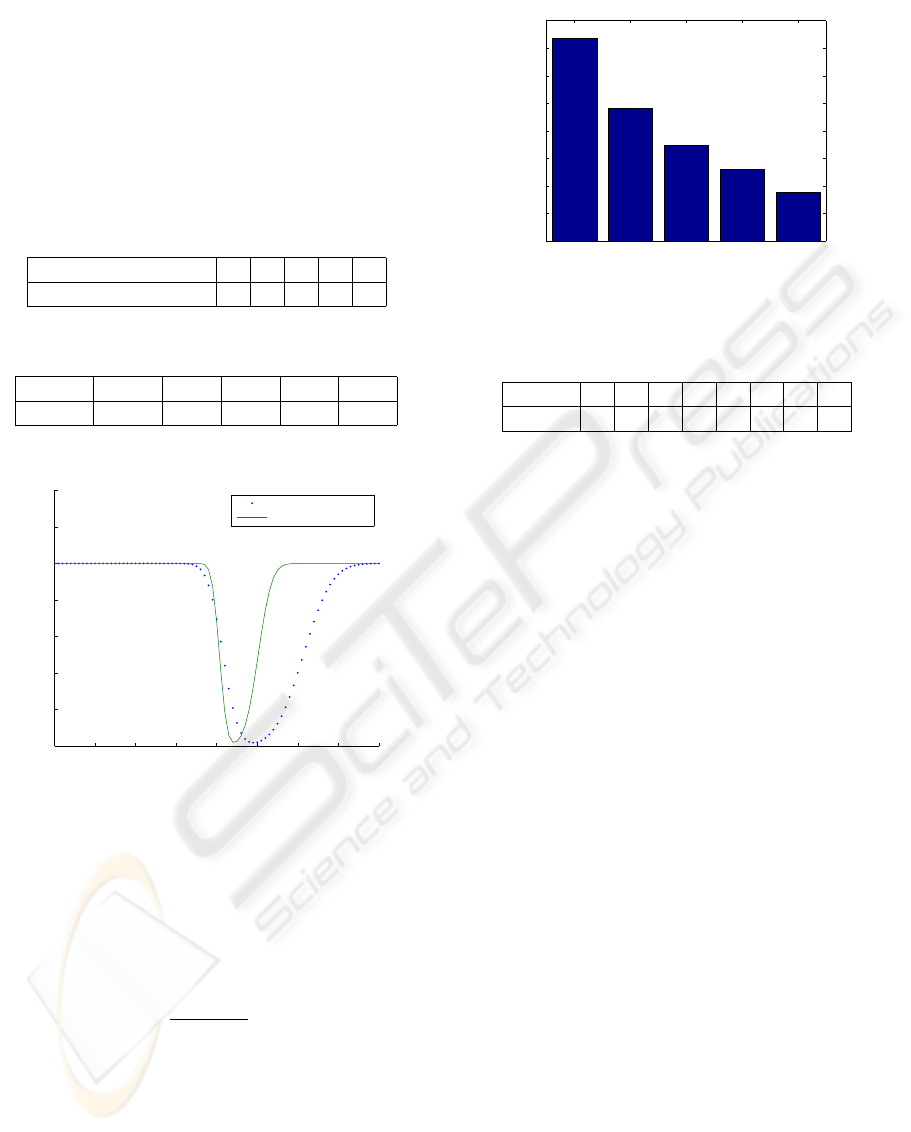
assumed to have five sensors with the noise variances
given in Table 1. We plot the error probability for the
optimal values of {α
i
}(given in Table 2) as a function
of τ in Figure 1. For comparison we have also plotted
the error probability for α
i
= 1/σ
2
i
. It can be seen that
both cases result in similarly small error probabilities
albeit for different values of τ. This indicates that if
optimization over τ is performed then α
i
= 1/σ
2
i
re-
sults in good performance.
Table 1: σ values for different sensor index.
Sensor node index(i) 1 2 3 4 5
σ 1 2 3 4 5
Table 2: Optimumα values for different sensor index.
Sensor 1 2 3 4 5
α 2.023 0.52 0.33 0.26 0.23
−4 −3 −2 −1 0 1 2 3 4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
global threshhold(tau)
probability of error
optimized alpha values
alpha=1/sigma
2
Figure 1: Probability of error vs global threshold.
5.2 Energy Allocation for Noisy
Channels
In this case ,we are interested in optimal energy al-
location for non-identical sensors. For sensor i the
channel is a binary symmetric channel with crossover
probability ε
i
= Q(
p
2E
T
x
i
/N
0
). The WSN configu-
rations are given in Tables 1 and 3. The optimal value
of energy fractions obtained through analytical for-
mulation are depicted in Figures 2 and 3. In these
figures we also show the resulting error probabilities.
As expected the sensors with smaller noise variance
are allocated a higher fraction of the energy.
We obtained similar results for the case N=8, with
following σ
i
values.
Fig.3 shows the results for the case N=8.
1 2 3 4 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
energy fraction allocated
sensor index
τ=0.4327,Probability of error=0.0099
Figure 2: Optimal energy fractions allocated for N=5.
Table 3: σ values for different sensor index.
Sensor 1 2 3 4 5 6 7 8
σ 1 2 3 4 5 4 3 2
5.3 Energy Allocation Using the
Distance Measure
For the WSN configurations in Tables 1 and 3 we have
obtained the optimal energy allocation using the J-
divergence distance measure. The energy allocations
are shown in Figures 4 and 5, respectively. It is in-
teresting to note that in these cases the nodes with a
large noise variance are not allocated any energy and
thus are prevented from transmitting their decision to
the fusion center. These nodes are censored. In these
figures we also show a lower bound on the error prob-
ability obtained from the J-divergence distance mea-
sure.
6 CONCLUSION
We have studied the problem of binary hypothesis
testing in a wireless sensor network in the presence
of noisy channels and for non-identical sensors. We
have designed a mathematically tractable fusion rule
for which optimal energy allocation for individual
sensors can be achieved. The objective is to opti-
mize a cost function with a constraint on the total
network energy. Two cost functions were considered;
the probability of error and the J-divergence distance
measure. Results of optimal energy allocation and the
resulting probability of error are presented for differ-
ent sensor network configurations.
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
20

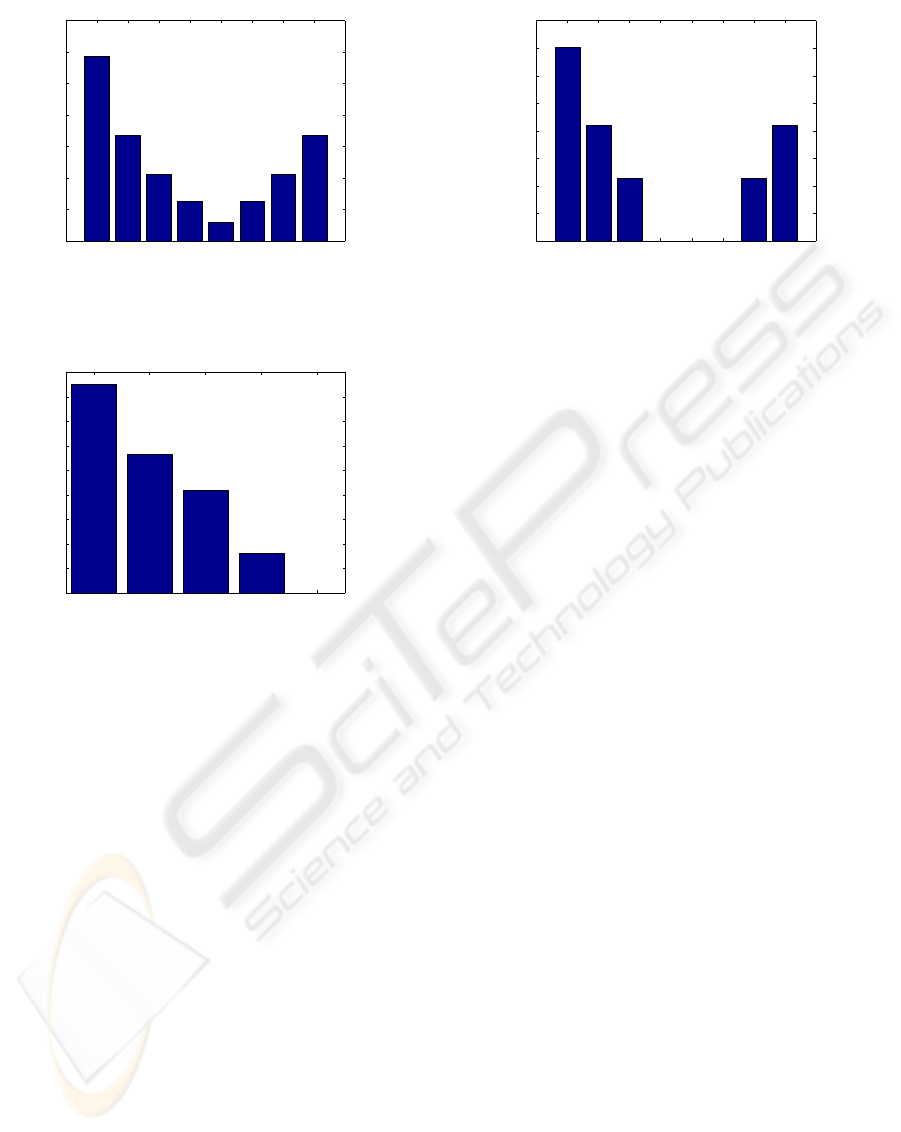
1 2 3 4 5 6 7 8
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
energy fraction allocated
sensor index
τ=0.5256,Probability of error=0.006
Figure 3: Optimal energy fractions allocated for N=8.
1 2 3 4 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
probability of error=0.008
sensor index
energy fraction allocated
Figure 4: Optimal energy fractions allocated for N=5 using
Distance Measure.
REFERENCES
Boyd, S. and Vandenberghe, L. (2004). convex optimiza-
tion. Cambridge press, London.
Cui, S., Goldsmith, A., and Bahai, A. (2005). Energy-
constrained modulation optimization. In IEEE Trans-
actions on Wireless Communications.
Eremin, E. (1999). A central limit theorem for linear esti-
mators of measurement results. In Measurement Tech-
niques.
Kailath, T. (1967). The divergence and bhattacharya dis-
tance measures in signal selection. In IEEE Transac-
tions on Communications.
Luo, X. and Giannakis, G. B. (2004). Energy-constrained
optimal quantization for wireless sensor networks. In
1st IEEE Annual Communications Society Conference
on Sensor and Ad Hoc Communications and Networks
(SECON ’04).
Poor, H. and Thomas, J. (1977). Applications of ali-slivey
distance measures in the design of generalized quan-
tizers for binary decision systems. In IEEE Transac-
tions on Communications.
Tsitsiklis, J. (1988). Decentralized detection by a large
number of sensors. In Math. Contr., Signals, Systm.
1 2 3 4 5 6 7 8
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
probability of error=0.0056
sensor index
energy fraction allocated
Figure 5: Optimal energy fractions allocated for N=8 using
Distance Measure.
Varshney, P. (1997). Distributed detection and data fusion.
Springer-Verlag, New York.
Zhang, Q., P.K.Varshney, and wessel, R. (2002). optimum
bilevel quantization quantization of i.i.d sensor obser-
vations for binary hypothesis testing. In IEEE Trans-
actions on Informtation Theory.
OPTIMAL ENERGY ALLOCATION FOR DETECTION IN WIRELESS SENSOR NETWORKS
21