TAG NUMBER ESTIMATION SCHEME IN GEN2 PROTOCOL

BASED RFID SYSTEM

Cheng-Hao Quan, Hee-Sook Mo and Gil-Young Choi

Electronics and Telecommunications Research Institute, Korea

Keywords: RFID, Gen2 Protocol, Anti-collision Algorithm, Tag Number Estimation.

Abstract: Recently, the RFID(Radio Frequency Identification) technology has gained significant attention. One of the

performance issues in RFID systems is to resolve the tag collision among responses from RFID tags. In this

paper, we proposed a Gen2 Protocol based Tag Number Estimation Scheme for estimation of the number of

tags in the reader filed. The scheme is used by anti-collision algorithm to identify multiple tags efficiently.

We also present the simulation result that shows the proposed scheme to estimate tags efficiently and also to

improve the systems efficiency.

1 INTRODUCTION

RFID(Radio Frequency Identification) system is an

automatic identification system that is used to

identify physical objects. In context of ubiquitous

computing, the object identification is the most

useful for applications. RFID technology plays a key

role in ubiquitous computing. RFID technology is

known to be well-suited to linking the physical and

virtual world.

The RFID system consists of two essential

components: the RFID tag, which is attached to the

object to be identified and serves as the data carrier,

and the RFID reader, which can read from and write

data to the tag. The reader broadcast the request

message to the tags, and tags will backscatter own id

to reader.

Recently, the RFID technology has gained

significant attention. One of the performance issues

in RFID systems is to resolve the tag collision

among responses from RFID tags. In the most of the

cases, numerous tags can be present in the reader

field. It will cause collision at reader among multiple

tags.

The tag collision in RFID systems happens when

multiple tags reflect the signal back to the reader.

This problem is often seen whenever a large number

of tags must be read together in the same reader

field. For resolving this problem, anti-collision

algorithms are adopted. An anti-collision algorithm

enables a single reader to read more than one tag in

the reader field.

The anti-collision algorithm can be categorized

into tree based protocols and ALOHA(Frits, 1983;

Frits, 1980) based protocols. For the most air

interface protocol are adopted ALOHA based anti-

collision algorithms, such as, Gen2 protocol

(EPCglobal, 2005), 13.56MHz class 1

protocol(Auto-ID, 2003) proposed by EPCglobal,

ISO/IEC 18000-6 type A(ISO/IEC, 2004), ISO/IEC

18000-7(ISO/IEC, 2004) proposed by ISO/IEC.

In recent years, the UHF(Ultra High Frequency)

band is recognized as the most suitable band in the

distribution fields. To meet the strong demand of

the RFID markets, the standardization for the use of

the UHF band is in rapid progress, compared with

other bands. EPCglobal UHF Gen2 has been already

approved as the international standard ISO/IEC

18000-6 type C(ISO/IEC, 2006) in June 2006.

EPCglobal UHF Gen2 protocol used the slotted-

ALOHA based anti-collision algorithm.

In the slotted-ALOHA(Vogt, 2002; Vogt, 2002;

Kim, 2004) based RFID system, tags randomly

select their slot number, that is response time, and

send the response back to the reader when the slot

number is zero. The maximum slot number is called

a frame size or round size. if too many slots are

performed, the delay will be high. If too few slots

are performed, some tags might be missed because

of tag collision. So, an optimal value for the

maximum number of slots should be used.

In this paper, we proposed a new scheme for

estimation of the number of tags in the reader filed.

The scheme is used by anti-collision algorithm in

Quan C., Mo H. and Choi G. (2007).

TAG NUMBER ESTIMATION SCHEME IN GEN2 PROTOCOL BASED RFID SYSTEM.

In Proceedings of the Second International Conference on Wireless Information Networks and Systems, pages 5-8

DOI: 10.5220/0002146200050008

 SciTePress

Gen2 protocol to identify multiple tags efficiently.

We also present the simulation result that shows the

proposed scheme to estimate tags efficiently and

also to improve the systems efficiency.

The rest of this paper is organized as follows.

Section II reviews the related works. Section III

describes our proposed new tag number estimation

scheme. In section IV, the results of performance

analysis will be explained. Finally the conclusions of

the paper will be present in Section V.

2 RELATED WORKS

In the slotted-ALOHA RFID systems, after the

reader has sent its request to the tags, it waits a

certain number of times for tag response. This time

is divided into a number of slots that can be

occupied by tags and used for sending their ID. In

the first step, the reader broadcast a frame start

message to tags. The message contains frame size

parameter that denotes the number of available slots

for response. In the second step, tags randomly

select one slot to send their ID back to the reader. As

the result of one frame we get a triple of numbers c

=<c

, c

> that quantify the empty slots, slots

filled with only one tag, and slots with collisions,

respectively. In order to choose the optimal frame

size(N) for the number of tgas(n) in the reader field,

we have to estimate n based on the results of one

frame.

So far, two estimation schemes yield

approximations for n. The first estimation scheme is

obtained as follows. Chebyshev’s inequality tells us

that the outcome of a random experiment involving

a random variable X is most likely somewhere near

the expected value of X. thus, an alternative

estimation function uses the distance between the

frame result c and the expected value vector to

determine the value of n for which the distance

becomes minimal. We denote this estimation:

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

kvd

cccNe

min

),,,(

(1)

In Eq. 1, N, n, a

N,n

, a

N,n

, and a

N,n

represent the

number of slots, the number of tags, the average

expected value of c

, the average expected value of

, and the average expected value of c

. The number

of tags is estimated as the value of n that minimizes

an error between the measured value and the

expected value of the slot state.

The problem of this scheme is hard to implement

and performance of scheme determined by errors of

estimated value, to some extent, which are more

closed to average expected value, also, is affected in

the range of value n.

The second estimation scheme is obtained

through the observation that a collision involves at

least two different tags. Therefore a lower bound on

the value of n can be obtained by the simple

estimation function:

cccccNe 2),,,(

110min

(2)

The problem of this scheme is that many big

errors will occur when the number of tags is more

than two times of the number of slots. According to

this, it can be applied usefully only in the range of

less than two times.

NccN

cccccNe

222

2),,,(

110min

≤−−=

(3)

In reality, in the most of the algorithms, they

adopted multi-step procedure to estimate number of

tags according to result of one frame, such as fixed-

slot increase-decrease scheme, proportion scheme,

log slot increase-decrease scheme and so forth.

3 THE PROPOSED TAG

NUMBER ESTIMATION

SCHEME

In this section, we first review the mathematical

tools(Walter, 1960) about the slotted-ALOHA

algorithms. The number of slots in a time frame

available for tag response is called frame size and

denoted by N. The number of tags is often denoted

by n.

Given N slots and n tags, the number r of tags in

one slots is binomially distributed with parameter n

and 1/N :

rnr

−

⎟

⎠

⎞

⎜

⎝

⎛

= )

1()

()(

(4)

The number r of tags in a particular slot is called

the occupancy number of the slot. The distribution

Eq. 4 applies to all N slots, thus the expected value

WINSYS 2007 - International Conference on Wireless Information Networks and Systems

of the number of slots with occupancy number 0 is

given by:

NBNa )

1()0(

−=⋅=

(5)

The number of slots that loaded only one tag ID,

is given by:

)

1()1(

−

−=⋅=

nBNa

(6)

From Eq. 5 and Eq. 6, we get

)1(

)

1(/)

−=

−

−−= Nn

(7)

Put it in order, estimation of the number of tags

is calculated by Eq. 8 as follows:

)//()1(

nNnN

aaNn −=

(8)

In this paper, the Eq. 8 is considered as a

theoretical basis. But actually, we substitute c

for

N,n

and substitute c

for a

N,n

in the algorithm, and

get Eq. 9 as follows:

)//()1(

ccNn

−

(9)

According to Eq. 9, we can estimate the number

of tags. But the accuracy is determined by the errors

of measured value c, same as the first estimation

scheme. After performing one read frame, we can

compute the number of tags to estimate n.

4 SIMULATION RESULTS

In this section, we analyze the performance of

proposed estimation scheme for the number of tags

and compare performance with the second scheme,

which is the minimum estimation scheme that

described above. The parameters assumed in the

simulation are same as the follows. The number of

tags in the reader field is 16 to 256, and the number

of slots N has the value of 16, 32, 64, 128, and so on

as maximum 256.

According to the increase of the number of tags,

Figure 1 shows the estimated number of tags (n-p)

with proposed scheme and the minimum estimation

number of tags (n-min) and real number of tags (n-r)

when the number of slots is assumed by 64.

According to the increase number of tags, even the

errors of the estimation value are somewhat big,

compare with the minimum estimation scheme, the

figure shows that the proposed scheme produces the

approached results. When the minimum estimation

scheme explained before is two times of the

assumed number of tags, which assumes tags more

than 128, is known as its errors are quiet big.

According to the estimated number of tags in

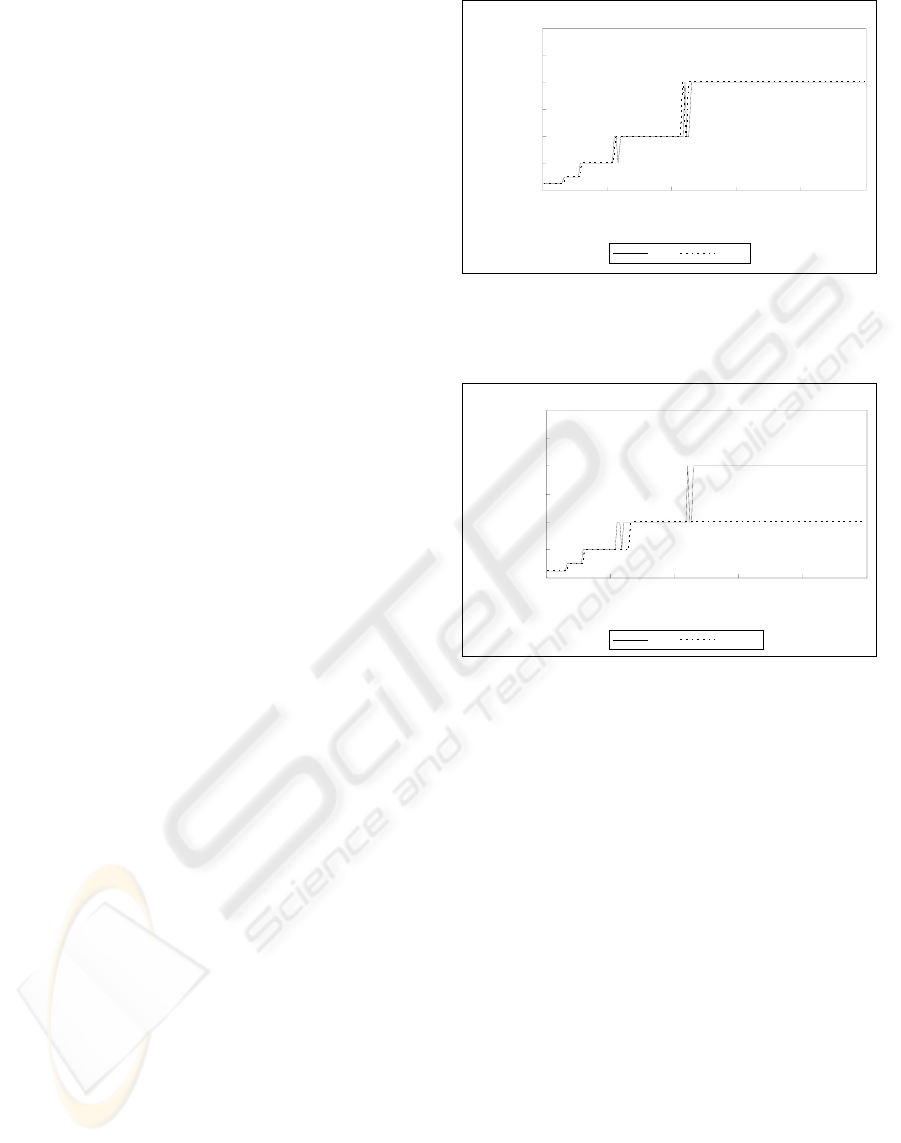
Figure 1, Figure 2 and Figure 3 compare and show

optimal value of the number of slots which can

improve the system efficiency. We can know that

the number of slots according to the estimated

number of tags through proposed scheme and the

produced number of slots according to the real

number of tags are almost close. In contrast, the

produced number of slots is seen to be assumed

smaller than the number of slots minimized between

the section of 64~84 and the section more than 142

according to the estimated number of tags through

estimated scheme of the minimum value. In the case

of being same with it, collided slots in all slots

increase oppositely and occur low performance.

Along with above, it means that system efficiency

can be improved in the case of using the proposed

scheme to estimate, it is to compare with the

estimated scheme of minimum value.

The proposed scheme of the number of tags

based on the triple status information of slots(c= <c

, c

>) can’t estimate the number of tags when

either c

or c

or both of them are close to 0 or errors

of the estimated value is big. In contrast, when the

number of slots is too much than the number of tags,

the estimated number of tags is more accurate

because the collided slot(c

) is close to 0 or contains

much information than c

or c

In general, when the

number of tags is four or eight times of the estimated

number of slots, because c

and c

are close to 0,

using the Eq. 9 above mentioned, the number of tags

can not be estimated. In the same case, the rate

Comparison of estimated value of number of

(

frame size

is 64

)

128

192

256

320

384

0 64 128 192 256 320

Number of ta

(

)

Estimated value of

number of tags

n- min n-

Figure 1: Comparison of estimated value of number of tags.

TAG NUMBER ESTIMATION SCHEME IN GEN2 PROTOCOL BASED RFID SYSTEM

occupied by c

in the total number of slots can be

calculated and estimated through an experiment.

In reality, there are 300 tags in reader field for

identifying, if the number of slots is assumed as 128

at the beginning, the number of tags can be assumed

accurately through the proposed scheme in almost

all the sections.

5 CONCLUSIONS

In this paper, we proposed a tag number estimation

scheme in Gen2 protocol based RFID systems and

the simulation result are also presented. The

simulation result shows that the proposed scheme to

estimate tags efficiently and further to improve the

systems efficiency.

REFERENCES

Auto-ID Center, May 2003. 13.56MHz ISM Band Class 1

Radio Frequency Identification Tag Interface

Specification: Candidate Recommendation, Ver. 1.0.0.

Auto-ID Center.

C. Kim, K. Park, H. Kim, S. Kim, June 2004. An Efficient

Stochastic Anti-collision Algorithm using Bit-Slot

Mechanism. Proceeding of International Conference

on Parallel and Distributed Processing Schemes and

Applications (PDPTA).

EPCglobal, January 2005. EPC

Radio-Frequency

Identity Protocols Class-1 Generation-2 UHF RFID

Protocol for Communications at 860 MHz – 960

MHz Version 1.0.9. EPCglobal.

Frits C. Schoute, 1980. Control of ALOHA Signalling in a

Mobile Radio Trunking Systems. In International

Conference on Radio Spectrum Conservation

Schemes.

Frits C. Schoute, April 1983. Dynamic Frame Length

ALOHA. IEEE Transactions on Communications,

COM31(4).

H. Vogt, , October 2002. Multiple Object Identification

with Passive RFID Tags. IEEE International

Conference on Systems, Man and Cybernetics.

H. Vogt, August 2002. Efficient Object Identification with

Passive RFID Tags. Proceeding of International

Conference on Pervasive Computing, LNCS.2414.

Springer-Verlag.

ISO/IEC, May 2004. Information Technology - Radio-

Frequency Identification for Item Management - Part

7: Parameters for Active Air Interface

Communications at 433 MHz. ISO/IEC.

ISO/IEC, May 2006. Information Technology - Radio-

Frequency Identification for Item Management - Part

6: Parameters for Air Interface Communications at

860 MHz to 960 MHz. ISO/IEC.

W. A Shewhart, S. S Wilks, 1960. An Introduction to

Probability Theory and Its Application - Second

Edition. Wiley publications.

Com

arison of o

timal value o f number of slots

(

)

128

192

256

320

384

0 64 128 192 256

Number of ta

(

)

Optimal value of number

of slots

N-

Figure 2: Comparison of optimal value of number of slots

(I).

Com

arison of o

timal value of number of slots

(

)

128

192

256

320

384

0 64 128 192 256

Number of ta

(

)

Optim al value of num ber

of slots

N-

N- min

Figure 3: Comparison of optimal value of number of slots

(II).

WINSYS 2007 - International Conference on Wireless Information Networks and Systems