APPLICATION OF CAUCHY INTEGRAL TO APPROXIMATE
THE FIELD COMPONENTS AND CURRENT IN METAL &
DIELECTRICAL POLYGONS
Method of the Field (Current) Restoration Inside and Outside Flat Closed Contour
based on Its Known Values at the Contour
A. V. Ashikhmin, Yu. G. Pasternak, S. L. Podvalny and Yu. A. Rembovsky
Moscow p/o 30 ,IRCOS, JSC
Keywords: Analytic function of complex variable, Cauchy integral, field (current) approximation, metal and dielectrical
polygons.
Abstract: The Cauchy integral was proposed as a means to approximate the field components and current in metal and
dielectrical polygons. The report illustrates that such a technique can significantly scale down
electromagnetic issues solved in spatial- frequency domain. The technique also makes it possible to evaluate
the strength of electromagnetic field not only inside the considered closed contour, but outside it even in
case when there is no a prior information about object configuration and its physical characteristics.
1 INTRODUCTION
The purpose of this work is to illustrate applicability
of Cauchy integrals to description of
electromagnetic (EM) field or current in some
electromagnetic objects whose surface allows a
piecewise planar approximation. By example of
dielectrical and metal cubes, it was confirmed that
such a description could help restore the field
(current) values within an object surface (or object
section) for a wide frequency band. These simple
electromagnetic objects were selected because their
main properties had been studied very thoroughly by
a lot of scientists - both through numerical
computation of electrodynamics boundary values
and through real experiments as in (Mittra, 1977).
The Cauchy integral was then proposed as a means
to scale down the systems of linear algebraic
equations derived from electromagnetic vector
boundary equations and drawn in terms of space and
frequency. The report illustrates that such a
technique makes it possible to evaluate the strength
of electromagnetic field not only inside the
considered closed contour, but outside it even in
case when there is no a prior information about
object configuration and its physical characteristics.
It is proved that proposed technique can be used for
reducing systematic errors in measurement of
emitter’s angular coordinates by means of mobile
direction finders and increasing DF resolution and
accuracy.
There are a lot of highly effective methods for
electromagnetic field approximation (both for entire
electrodynamic objects and for their components,
e.g. in their finite elements) including the cases
when the object dimensions exceed the free-space
wavelength. Thus, to describe the field behavior via
modified finite elements method, we suggest using
Lagrange interpolation polynomials in this work
(Milan, Branislav, 2006). The finite elements
approach proposed by the authors (Milan, Branislav,
2006) allows to significantly reduce the number of
computations to describe the field, as compared with
regular polynomials. However, if you do not have a
priori information about the object geometry and
materials, it cannot restore the structure of the EM
field inside the object and outside of it. The authors
of this report suppose that the above problem can be
solved if the field/current component is taken as an
analytical complex variable function with a Cauchy
integral and this work is just an approach to that
solution.
153
V. Ashikhmin A., G. Pasternak Y., L. Podvalny S. and A. Rembovsky Y. (2007).
APPLICATION OF CAUCHY INTEGRAL TO APPROXIMATE THE FIELD COMPONENTS AND CURRENT IN METAL & DIELECTRICAL POLYGONS -
Method of the Field (Current) Restoration Inside and Outside Flat Closed Contour based on Its Known Values at the Contour.
In Proceedings of the Second International Conference on Wireless Information Networks and Systems, pages 153-156
DOI: 10.5220/0002144901530156
Copyright
c
 SciTePress

2 THEORY
For practical purposes, it is advisable to treat the
analyzed surface
S
as a total of plane polygons of
different size. Suppose that there is a plane polygon
over a closed contour
L
.
Then, the Cauchy integral can be evaluated
through the known discrete values of
(
)
k
U
ξ
(
N
k
,...,2,1=
) using
L
(Privalov, 1984) integration
contour:
()
() ()
∑
∫
=
−
Δ⋅
⋅
⋅⋅
≈
−
⋅
⋅⋅
=
N
k
k
kk
L
z
U
iz
dU
i
zU
1
2
1
2
1
ξ
ξξ
πξ
ξξ
π
,
is an increment of the integration complex variable,
where the
kkk
yix
Δ
⋅
+Δ=Δ
ξ
point is center of the
intervals
22
kkk
yxl Δ+Δ=
whose length is
k
ξ
.
Below are computational modeling results
illustrating applicability of Cauchy integration for
approximation of field/current components in the
simplest electrodynamic objects - dielectrical or
steel cube.
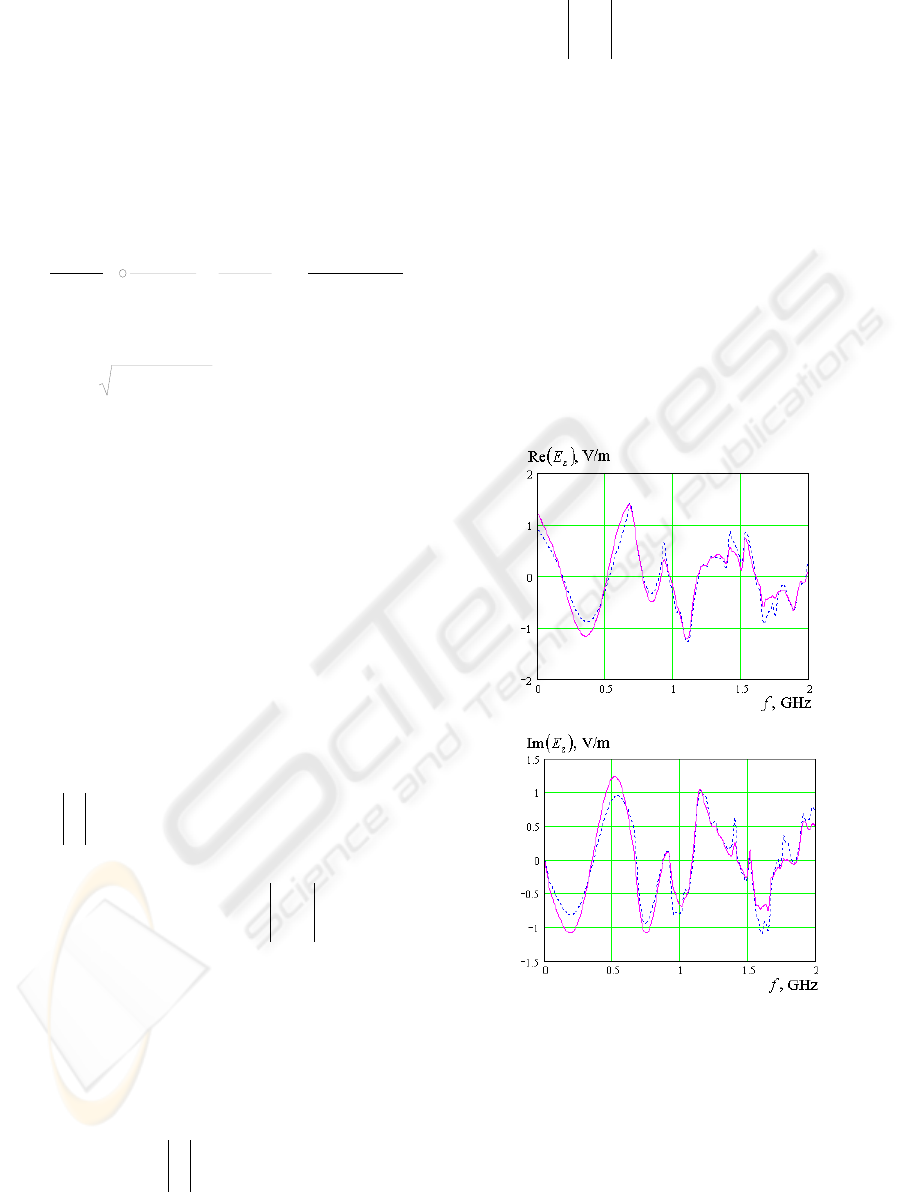
The dash lines in Figs. 1, 2 reflect the actual
(derived through rigorous numerical solutions of
diffraction problems) frequency profiles of the real
and imaginary part of
z
E
-component (total EM
field) and
z
J
-component (current density on the
metal surface). The solid lines show the restored
profiles derived through Cauchy integrals.
Let’s consider diffraction of a plane polarized
EM-wave on a 110x110x110 mm dielectrical cube
where (
,10=
r
ε
003.0=
э
tg
δ
) - Figure 1. The
coordinates of the normalized wave vector
→→→
=
000
/ kkk
n
were taken as
()
577.0;577.0;577.0 −−−
. Projection of the
normalized vector
→→→
=
...
/
падпадпад
n
EEE
onto the
coordinate axis
);;(
z
y
x
were (-0.408; -0.408;
0.816) respectively. The sight point coordinates
were taken as (45; 45; -55) mm (near the bottom
cube face angle).
The results of numerical experiments to restore
the current density on the “shady” surface of the
metal cube are shown in Figure 2. For the above
profiles, the values of the normalized wave vector
coordinates
→→→
=
000
/ kkk
n
amounted to (-0.667; -
0.667; -0.333); and projections of that vector
→→→
=
...
/
падпадпад
n
EEE
to
);;(
z
y
x
axis were taken as
(
) 943.0;236.0;236.0
−
−
. The surface current
density was to be restored in the middle of a “shady”
face of the cube (
55
−
=
y
mm); and the sight point
coordinates were taken as (0; -55; 0) mm.
With this, we would like to draw attention to the
actual and imaginary part of the
z
E
- component
(total EM field, Figure 1). There, the Cauchy
integral can “scan” almost all the frequency band in
question and “trace” even the slightest resonances
around such frequencies as 1.4, 1.5 and 1.85 GHz.
The available errors between the actual and
estimated profiles are, most probably, caused by
numerical integration errors and by the nature of the
function describing the field structure (current) – it
is not purely analytical.
a)
b)
Figure 1: Restoration of the Field at the Bottom of a
Dielectric Cube, section
55
−
=
z
mm).
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
154

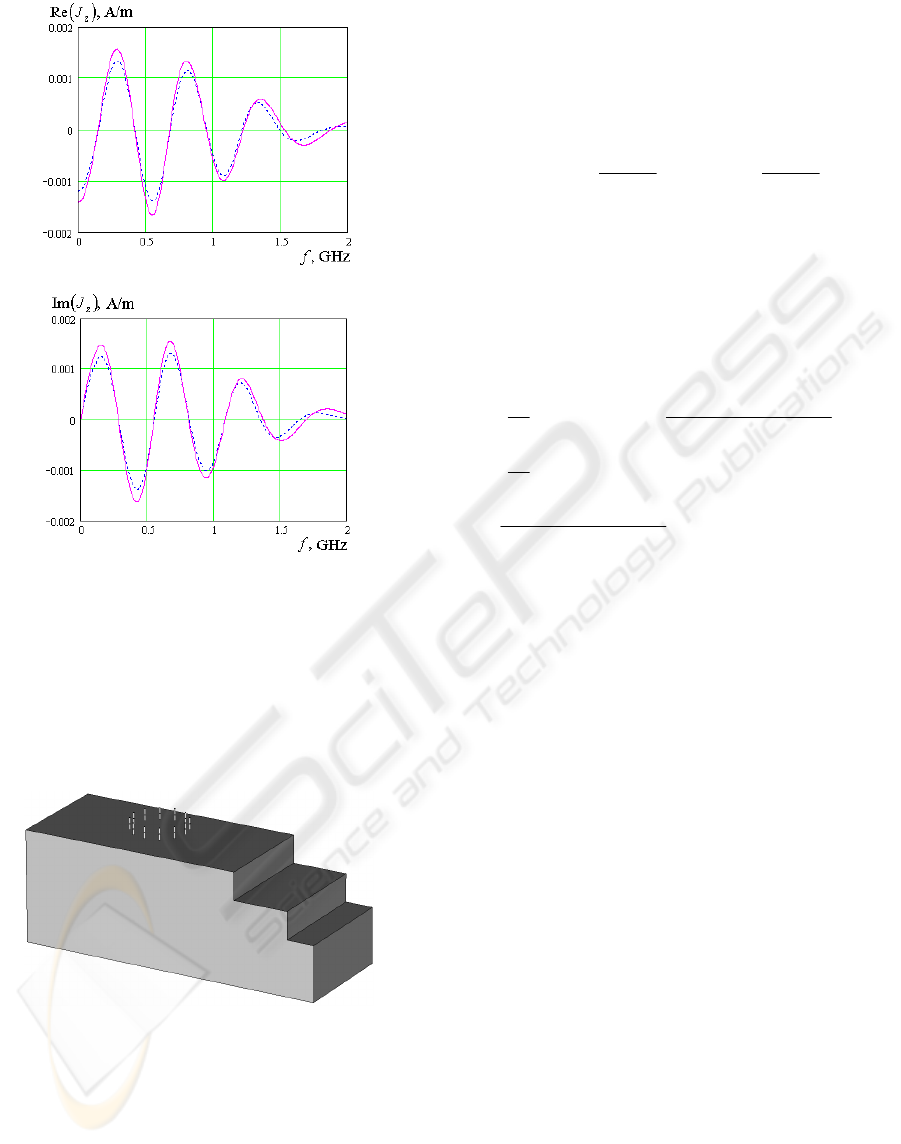
a)
b)
Figure 2: Restoration of the Current Surface Density on
the “Shady” Side of a Metal Cube (
55−=
z
mm).
Now let us consider a method for restoration of
the EM field outside a closed contour and try to
reduce the angular coordinates systematic error in
emitters’ position finding by means of a mobile
antenna array - see Figure 3.
Figure 3: Electromagnetic object: carrier enclosure +
antenna array.
Suppose that an EM wave is falling onto an
array, then the general vector of the voltage
amplitudes, which emerged on the antenna resistors,
is
[]
T
N
UUUUU ,...,,,
321
=
→
. In this case, the values of
the function describing the field at the circle with
R
radius comprising the elements of the array and,
consequently,
N
electrically short symmetrical
vibrators will be as follows:
[] () ()() []
∑
+
=
−
+⋅−⋅⋅=⋅⋅=
1
1
1
1/1expexp
N
n
n
NniBiRzU ξξ
.
The values of
n
B
complex factors are determined
through solution of the following algebraic
equations with several complex unknowns:
(
) ()
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅++
⎥
⎦
⎤
⎢
⎣
⎡
+
+=
+
N
N
N
ikB
N
N
ikBBU
Nk
1/2
exp...
1/2
exp
121
ππ
,
The values of the
R
function measured and
approximated at the outer circle with
U
radius shall
conform to Cauchy or Poisson integral formula:
So we obtain an a first kind Fredholm integral
equation related to unknown
[
]
()
ψ
⋅
⋅ irU
внешнее
exp
function, describing the scalar field on
r
-radius:
[]
() ()
[]
∑
+
=
−
+−=
1
1
1
1/)1(expexp
K
k
kвнешнее
KkiXirU ψψ
,
And this function is fully determined by
X
-factors.
To solve this integral equation is an incorrect
mathematical problem and therefore we had to use
Tikhonov regularization (Bakhvalov, Zhidkov,
Kobelkov; 1987). We have also applied a
collocation method (Bakhvalov, Zhidkov, Kobelkov;
1987) and thus reduced the initial integral equation
to a system of linear algebraic equations with
complex variables.
According to the numerical analysis of the
bearing frequency dependence (provided that the
bearing was measured with an array with Radius
5.0
=
R
m and that the real azimuth angle was
0
_
45=
fallEMW
ϕ
for the falling wave), the maximum
systematic errors was 16
0
at 90 MHz: the measured
bearing value was 61
0
. The developed technique can
significantly reduce the amount of DF systematic
errors caused by scattered waves from the carrier.
Thus, when restoring the P&A structure of the scalar
field on the circle with
5.1
=
r
m, the error will be
reduced from 16
0
to 1
0
regardless of the carrier's
geometry and its location relative to the array
(Figure 4). Moreover, since the radius of a virtual
Nk ,...,2,1
=
() ( ) ( ) []
[] ()
()
()
[]
()
.
cos2
1/)1(exp
2
1
cos2
exp
2
1
1/1exp
22
22
2
0
1
1
1
22
22
2
0
1
1
1
ψ
ϕψ
ψ
π
ψ
ϕψ
ψ
π
ϕ
π
π
d
RrRr
Rr
KkiX
d
RrRr
Rr
irU
NniBRU
K
k
k
внешнее
N
n
n
+−−
−
⋅
⋅
⎭
⎬
⎫
⎩
⎨
⎧
+−=
=
+−−
−
=
=+−=
∫
∑
∫
∑
⋅
+
=
−
⋅
+
=
−
APPLICATION OF CAUCHY INTEGRAL TO APPROXIMATE THE FIELD COMPONENTS AND CURRENT IN
METAL & DIELECTRICAL POLYGONS
155

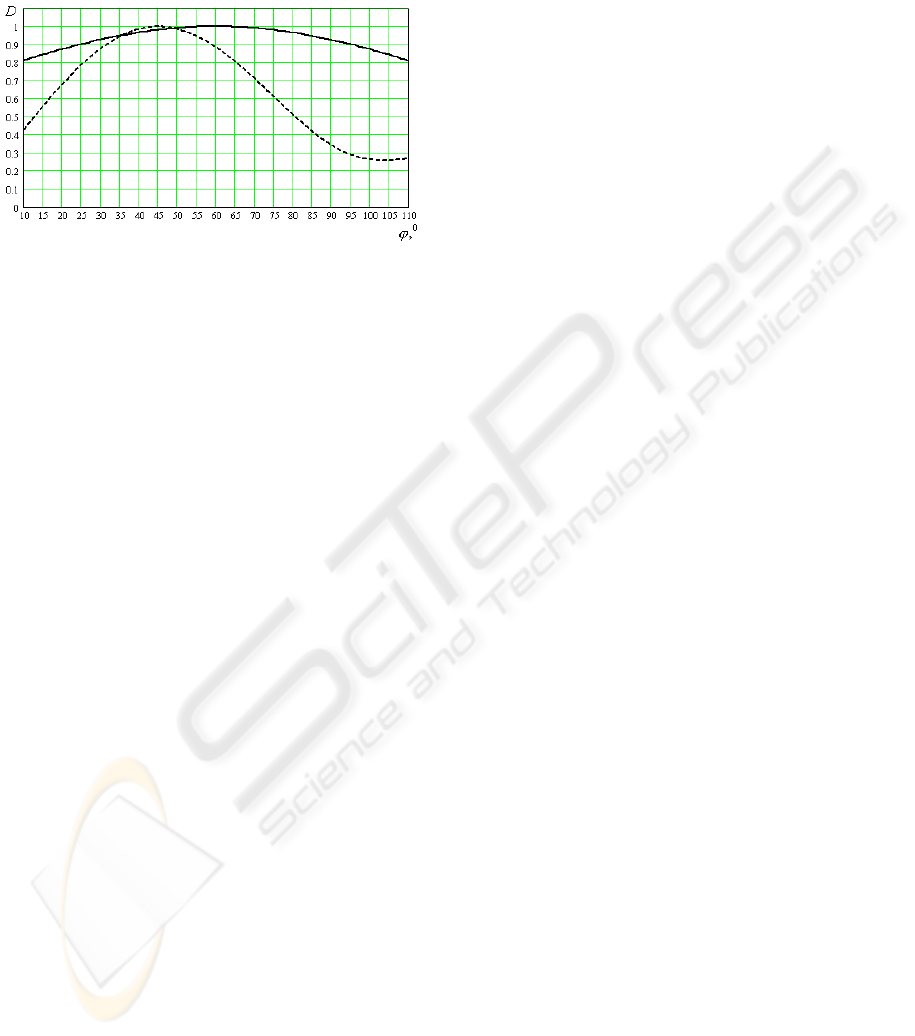
array is increased by three times and since the
number of its elements rises from 12 to 36, the
scanning resolution of the azimuth angular
coordinates will also rise.
Figure 4: Application of the proposed method for
reduction of direction finding systematic errors and
increase of azimuth resolution on a mobile carrier (the full
line shows the array pattern as in Figure 3 and the dash
line shows the array pattern for the array with the triple
diameter).
3 CONCLUSION
The EM field and current surface density
components in metal-dielectric structures can be
approximated by means of Cauchy integrals treated
by the method of average and based on the finite
aggregate of scalar field values taken through the
integration contour. With this, it can also be possible
to restore the phase and frequency characteristics of
the field or current within the integration contour.
Besides, these characteristics will be more exact
than those of amplitude and frequency and will
cover a wider frequency band.
In most of the reviewed cases, the field (current)
approximation accuracy will decrease as the sight
point approaches to the integration contour (if the
grid pitch is fixed). To increase such approximation
around the integration contour, a tapered grid can be
used. Its pitch will decrease as the sight point
approaches the contour.
Approximation of the field (or current) through
Cauchy integral can be applied to scale down
electromagnetic issues solved in terms of space and
frequencies and to allow for diffusers affecting
antenna systems and their directional properties.
It is proved that proposed technique can be used
for reducing systematic errors in measurement of
emitter’s angular coordinates by means of mobile
direction finders and increasing DF resolution and
accuracy.
REFERENCES
Mittra, R., Computer Techniques for Electromagnetics,
Moscow, MIR Publishers, 1977.
Milan, M., Ilic, Branislav, M., Notaros. Higher Order
Large-Domain Hierarchical FEM Technique For
Electromagnetic Modeling Using Legendre Basis
Functions On Generalized Hexahedra, Revised paper
for Electromagnetics, February 11, 2006
www.bnotaros.umassd.edu.
Privalov, I., I., Introduction to Complex Variable
Functions” Moscow, Nauka Publishers, 1984.
Bakhvalov, N., S., Zhidkov, N., P., Kobelkov; G., M.,
Numerical Methods, Moscow, Nauka Publishers,
1987.
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
156