FACE VERIFICATION IN UNCONTROLLED LIGHT CONDITIONS
OF STREET
Mariusz Leszczy
´
nski and Władysław Skarbek
Department of Electronics and Information Technology, Warsaw University of Technology
Nowowiejska 15/19, 00-665 Warsaw, Poland
Keywords:
Face verification, Linear Discriminant Analysis, face metrics, Receiver Operating Characteristics.
Abstract:
Impact of light conditions on face verification are considered for three linear discriminant feature extraction
schemes. Two verification scenarios, the single image query and multi image query, were compared. The
extraction algorithms are based on compositions of feature projections on global, intra and inter-class error
subspaces: Linear Discriminant Analysis LDA, Dual Linear Discriminant Analysis DLDA, and their combi-
nation LDA+DLDA. The metrics for evaluation of the verification error is the Mahalanobis distance between
normalized feature vectors. The normalization of feature vectors is justified with the upper bound by Fisher
separation index for feature vectors. Experiments conducted on facial databases with complex background
show the high performance of DLDA and DLDA+LDA verifiers with Equal Error Rate EER less than one
percent. The degradation of results, when controlled light conditions are replaced by uncontrolled ones, is of
factor two.
1 INTRODUCTION
Nowadays, due to society demand, face recognition is
of significant interest in scientific research. Besides
facial image searching and indexing, face identifica-
tion and face verification are the main tasks imple-
mented in face recognition systems.
Compact representation of extracted facial fea-
tures is one of the requirements for facial image in-
dexing (cf. contributions in (MPEG-7, 2004)) of
which fulfillment is necessary to get real time re-
sponse for queries in large databases. In case of hu-
man id verification systems the size of facial descrip-
tion is not important because the access to features
of relevance is direct on the basis of delivered iden-
tifier. However, there are several advantages to rep-
resent them in computer storage as short as possible
within acceptable increase (if any) of verification er-
ror (Jain et al., 1999):
• verification can be supported by searching of most
similar face images;
• shorter facial descriptions reduce bandwidth re-
quirements in network distributed applications
(like intelligent cash machines);
• mass production of biometric passports is easier if
their memory requirements are moderate;
• in global security systems archiving billions of
biometric passports could be more tractable.
It follows from the experience of MPEG-7 core
experiments (MPEG-7, 2004) that scalar uniform
quantization from 64 bits of double floating point pre-
cision to five bits of fixed point precision for vector
components of facial descriptions based on PCA and
LDA analysis improves the searching performance.
In this research we investigate whether the same con-
clusion can be drawn in case of verification in the sys-
tem based on DLDA (Dual Linear Discriminant Anal-
ysis).
The algorithms for LDA and DLDA based on
two SVDs is described in (Skarbek, W., Kucharski,
K. and Bober M., 2004). Recently we have elabo-
rated common conceptual framework for both meth-
ods which avoids traditional formal solution through
generalized eigenvalue problem with respect to within
and between-class scatter matrices by representa-
tion of discrimination process as a sequence of pro-
jection and scaling operations desribed by Disc-
rimanants Analysis Diagram (DAD) (Skarbek W. and
Leszczy
´
nski, M., 2007). The above references give
a complete mathematical and algorithmic discussion
of LDA and DLDA concepts. However, an engineer-
ing point of view on linear discriminant modeling of
data, given in Section II, can help readers to get right
intuitions for using such tools.
In case of cash machine applications not always
427
Leszczy
´
nski M. and Skarbek W. (2007).
FACE VERIFICATION IN UNCONTROLLED LIGHT CONDITIONS OF STREET.
In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 417-421
DOI: 10.5220/0002142004170421
Copyright
c
 SciTePress

Figure 1: Uniform versus complex background: face im-
ages for a person from Altkom database and two persons
from Vision database.
light conditions can be controlled. In this research
we check experimentally the impact of lighting onto
results of verification measured via ROC graphs.
2 DISCRIMINANT FEATURES
EXTRACTION
In the presented research the verification is based on
thresholding of weighted Euclidean distance of nor-
malized query feature vector to average feature vector
of facial images for the person of claimed identity.
The feature vector is obtained from input face im-
age in the following chain of operations:
1. source (spectral) feature extraction: window face
detection, face window normalization to fixed
eye center positions, transformation of normal-
ized face image into spectral domain 2D DFT, ex-
traction of significant Fourier coefficients, source
spectral data centering by grand mean;
2. discriminant feature extraction to get DLDA
(LDA) vector: projection onto inter-class (intra)
singular subspace, inter-class (intra) component-
wise scaling, projection into intra-class (inter) sin-
gular subspace;
3. final processing to get target features ready for
matching: projection of DLDA (LDA) vector onto
the unit sphere, and intra-class (inter) component-
wise scaling.
Figure 2: Face images from Yale, MPEG, and WUT
databases.
Traditionally LDA model W = [w
1
, . . . , w
M
] is ob-
tained from the solutions of the following generalized
eigenvalue problem:
S
b
w
m
= λ
i
S
w
w
m
w
m
∈ R
N
, m = 1, . . . , M, M ≤ N
(1)
by selecting independent eigenvectors of highest
eigenvalues (Fukunaga, 1992) of the adjoint classical
eigenvalue problem. Here S
b
– between-class scat-
ter matrix, S
w
– within-class scatter matrix. In or-
der to get the adjoint eigenvalue problem Fukunaga
used the Cholesky lower triangular decomposition of
S
w
= C
w
C
t
w
which is faster and more accurate than
matrix inversion (Golub and Loan, 1989):
C
−1
w
S
b
C
−t
w
(C
t
w
w
m
) = λ
w
(C
t
w
w
m
)
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
428

Figure 3: First 15 eigenfaces (fisherfaces) from U
(b)
in LDA (upper part) and U
(w)
in DLDA (lower part).
In case of DLDA the model is obtained from the
solutions of the following dual generalized eigenvalue
problem:
S
w
w
m
= λ
i
S
b
w
m
w
m
∈ R
N
, m = 1, . . . , M, M ≤ N
(2)
by selecting independent eigenvectors of least posi-
tive eigenvalues (Fukunaga, 1992) of the adjoint clas-
sical eigenvalue problem obtained also by use of
Cholesky matrix decomposition.
Despite its computational advantages the above
solution requires full rank property of the matrix S
w
in case of LDA and the same property for S
b
in case
of DLDA.
If rank(S
w
) < N then data regularization is per-
formed by PCA (Principal Component Analysis). Ac-
tually the change of coordinates in global error space
is performed, followed by rejection of least variance
components till the resulting principal subspace has
trivial intersection {0
N
} with kernel space of S
w
.
Since there is unknown direct formula for the num-
ber of rejected PCA component a trial-error process
is applied and its result strongly depends on the ac-
tual training data set X := [x
1
, . . . , x
L
]. Mathemati-
cally the result depends on mutual relationship be-
tween the kernel of total (global error) scatter matrix
S
t
= S
w
+ S
b
and the kernel of S
w
.
Introducing in (Skarbek W., Kucharski K. and
Bober M., 2006) our LDA and DLDA approach based
on orthogonal projections onto two singular sub-
spaces we intended to replace the relative analysis
of those kernels by the single kernel analysis for S
w
in case of LDA and kernel analysis for S
b
in case of
DLDA.
In order to give intuitive interpretation for our dis-
criminant modelers (LDA and DLDA) we use the fol-
lowing concepts:
1. change of Cartesian coordinate system in selected
error space by rotation and scaling of axis vectors;
2. projection onto subspace of maximum energy of
inter-class error (LDA case);
3. projection onto subspace of minimum energy
intra-class error (DLDA case).
In terms of the above operations the DLDA ex-
traction process can be described as follows:
1. Compute global error x
1
by source data x
0
center-
ing:
x
1
:= x
0
− ¯x;
2. Get major PCA inter representation, i.e. represent
the global error in major PCA base U
(b)
found at
training time for inter-class errors:
x
2
:= (U
(b)
)
t
x
1
3. Scale PCA inter representation using diagonal
matrix Σ
(b)
which normalized training PCA inter
coefficient to unit values:
x
3
:= Σ
(b)
x
2
Note: For training data the variance of x
3
variable
equals to the dimensionality of x
3
.
4. Get minor PCA intra representation, i.e. repre-
sent scaled PCA inter feature vector in minor PCA
base U
(w)
found at training time for intra-class er-
rors:
x
4
:= (U
(w)
)
t
x
3
Hence the aggregated DLDA matrixW has the fol-
lowing effect:
y = W
t
(x
0
− ¯x) = (U
(w)
)Σ
(b)
(U
(b)
)
t
(x− ¯x) (3)
It is interesting that in matching stage the best re-
sults are achieved by Mahalanobis distance for unit
length feature vectors:
δ(y
A
, y
B
) :=

y
A
ky
A
k
−
y
B
ky
B
k

t
Λ

y
A
ky
A
k
−
y
B
ky
B
k

(4)
where Λ := (Σ
(b)
)
2
in case of LDA and Λ := (Σ
(w)
)
2
in case of DLDA.
The normalization of feature vectors is closely re-
lated to the Fisher separation index between LDA or
DLDA feature vectors y
A
and y
B
of face images A and
B :
1
2



y
A
ky
A
k
−
y
B
ky
B
k



= 1−
2y
t
A
y
B
2ky
A
kky
B
k
≤
≤ 1−
2y
t
A
y
B
ky
A
k
2
+ky
B
k
2
=
ky
A
−y
B
k
2
ky
A
k
2
+ky
B
k
2
Since discriminant analysis indirectly reduces the
Fisher separation index then it also reduces the nor-
malized intra-class error.
FACE VERIFICATION IN UNCONTROLLED LIGHT CONDITIONS OF STREET
429

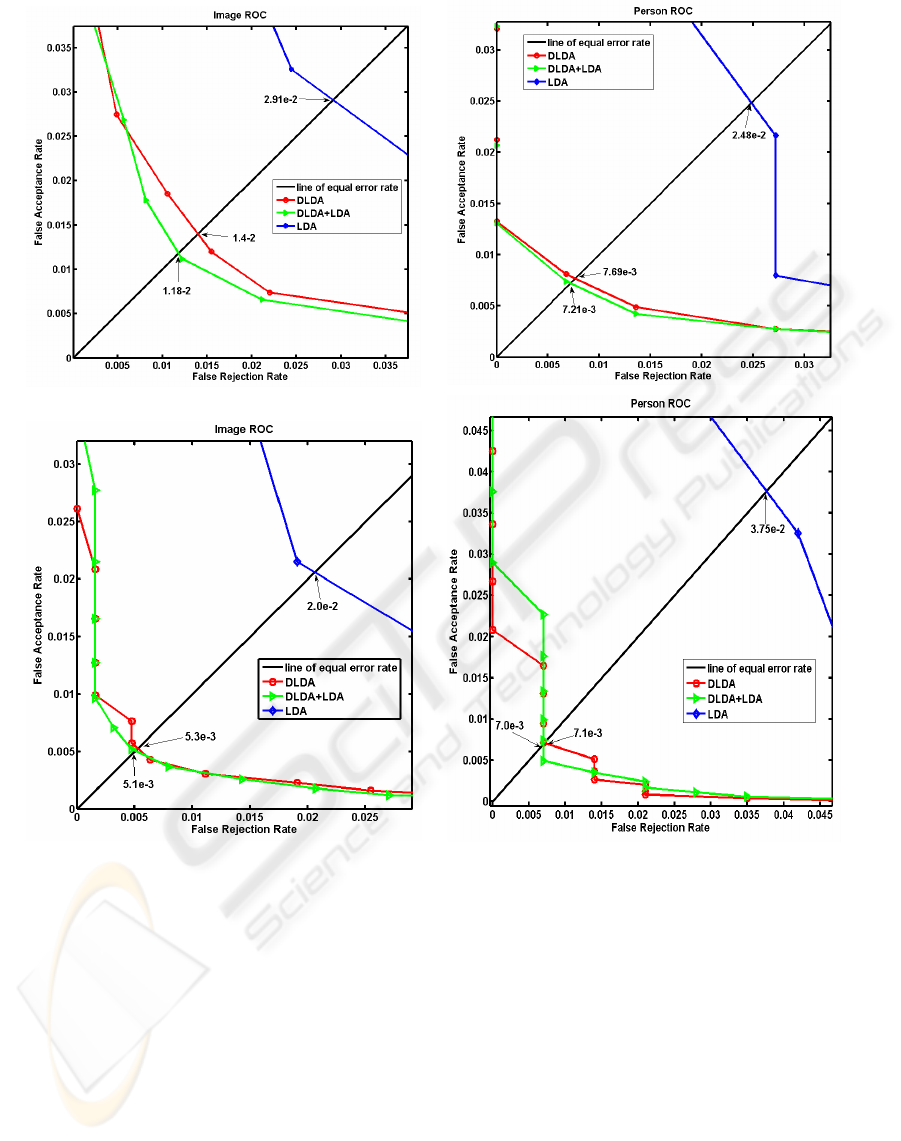
Figure 4: ROC results for face verifiers in uncontrolled (upper row) and neutral (lower row) lighting conditions. Face images
from Altkom, Vision, Yale, MPEG, and WUT databases.
3 EXPERIMENTAL RESULTS
We selected the normalized luminance facial images
(46 × 56 resolution with the same position of eyes)
from the following databases (cf. Fig. 1,2): Altkom
(80 persons with 15 images each), Vision (26 persons
with varying number of images per person), Yale (15
persons with 11 images each), MPEG (110 persons
with 5 images each), WUT (54 persons with 3 images
each).
From the previous works described in (Skarbek,
W., Kucharski, K. and Bober M., 2004) it is al-
ready known that in case of face verification the op-
timization of inverse Fisher ratio (DLDA) leads to
better results than the optimization of Fisher ratio
(LDA). Figure 3 gives more insight for this phe-
nomenon. Namely, DLDA eigenfaces (fisherfaces)
are more contrasted and more focused on particular
facial parts.
It is interesting that aggregation of DLDA and
LDA verifiers by the maximum, the arithmetic mean,
and the harmonic mean of distances give intermediate
results (in ROC sense) between the best DLDA re-
sults and and significantly worse LDA results. How-
ever, the geometric mean of both distances leads to
slight improvements of EER and ROC over DLDA.
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
430

In Fig. 4 we compare this results in two query scenar-
ios: single image (Image ROC) and multi-image (Per-
son ROC) and two lighting scenarios: unconstrained
(upper part ROCs) and neutral (lower part ROCs).
In case of Image ROC, we observe the improve-
ment of Equal Error Rate EER for the neutral lighting
for about two times. The insignificant improvement
in case of Person ROC is justified by small number of
neutral photos for most of persons engaged in training
and testing.
4 DISCUSSION AND
CONCLUSIONS
Impact of light conditions on face verification are con-
sidered for three linear discriminant feature extraction
schemes. Two verification scenarios, the single image
query and multi image query, were compared. The ex-
traction algorithms are based on compositions of fea-
ture projections on global, intra and inter-class error
subspaces: Linear Discriminant Analysis LDA, Dual
Linear Discriminant Analysis DLDA, and their com-
bination LDA+DLDA.
The metrics for evaluation of the verification er-
ror is the Mahalanobis distance between normalized
feature vectors. The normalization of feature vectors
is justified with the upper bound by Fisher separation
index for feature vectors.
Experiments conducted on facial databases with
complex background show the high performance of
DLDA and DLDA+LDA verifiers with Equal Error
Rate EER less than one percent. The degradation of
results when controlled light conditions are replaced
by uncontrolled ones is of factor two.
In cash machine application the input of verifica-
tion system is given as temporal sequence of images.
On the basis of the previous works we recommend
the design of face verifier for this application by the
following six steps:
1. Detect frontal pose of face by Discrete Gabor Jet
DGJ algorithm w.r.t. inner eye and nose corners
(Skarbek W. and Naruniec J., 2007).
2. Compensate lighting by Quotient Illumination
Relighting algorithm (QIR) (Cao B., Shan S., Gao
W. and D. Zhao, 2003).
3. Compensate pose by inner eye and mouth corners
to find the homographic mapping.
4. Align the compensated image by alignment of the
line segment joining outer eye corners.
5. Design the feature extraction scheme by optimiz-
ing DAD diagram.
6. If the verifier of 5 is not satisfactory then optimize
DLDA cascade.
ACKNOWLEDGEMENTS
The work presented was developed within VIS-
NET 2, a European Network of Excellence
(http://www.visnet-noe.org), funded under the
European Commission IST FP6 Programme.
REFERENCES
Fukunaga, K. (1992). Introduction to Statistical Pattern
Recognition. Academic Press.
Golub, G. and Loan, C. (1989). Matrix Computations. The
Johns Hopkins University Press.
Jain, A. K., Bolle, R., and Pankanti, S., editors (1999). Bio-
metrics: Personal Identification in Networked Society.
Kluwer Academic Publishers.
Cao B., Shan S., Gao W. and D. Zhao, (2003). Illumina-
tion normalization for robust face recognition against
varying lighting conditions in . IEEE ICCV-2003,
157:164, 2003
MPEG-7, editor (2004). Multimedia content description in-
terface. Visual Descriptor Extensions., volume 15938-
3:2002/Amd.1:2004. ISO/IEC.
Skarbek W., Kucharski K. and M. Bober, (2004). Dual LDA
for Face Recognition in . Fundamenta Informaticae
303:334:2004
Skarbek W., Kucharski K. and Bober M. , (2006). Cas-
cade of dual LDA operators for face recognition in .
Geometric properties from incomplete data, Kluwer
Academic Publishers 199:219, 2006
Leszczy
´
nski M. and Skarbek W., (2007). Biometric Verifi-
cation by Projections in Error Subspaces in . Rough
Set and Knowledge Technology, Springer LNAI 4481,
166:174, 2007
Naruniec J. and Skarbek W., (2007). Face Detection by
Discrete Gabor Jets and Reference Graph of Fiducial
Points in . Rough Set and Knowledge Technology,
Springer LNAI 4481, 187:195, 2007
FACE VERIFICATION IN UNCONTROLLED LIGHT CONDITIONS OF STREET
431