REVERSIBLE AND SEMI-BLIND RELATIONAL DATABASE

WATERMARKING

Gaurav Gupta and Josef Pieprzyk

Centre for Advanced Computing - Algorithms and Cryptography

Department of Computing, Division of Information and Communication Sciences

Macquarie University, Sydney, NSW - 2109, Australia

Keywords:

Reversible, relational database, watermarking, copyright, ownership.

Abstract:

In 2002, Agrawal and Kiernan proposed a relational database watermarking scheme that modiﬁes least sig-

niﬁcant bits (LSBs) of numerical attributes selected using a secret key. The scheme does not address query

preservation (some queries give different results when executed on the original and watermarked relation).

Additive and secondary watermarking attacks on the watermarked relation are also possible. Such attacks can

render the original watermark undetectable. Hence, an attacker who embeds his watermark in a previously wa-

termarked relation can claim ownership of that relation. However, if the scheme is reversible, then a previous

watermark, if any, can be detected in the reversed relation. In this paper, we propose an enhanced reversible,

semi-blind and query-preserving watermarking scheme. Using this scheme, the correct owner of a relation can

be identiﬁed even if the relation has been watermarked by multiple parties. If required, the database can be

restored to it’s original state too. This ﬁnds applications in high-precision settings such as military operations

or scientiﬁc experiments.

1 INTRODUCTION

Watermarking (embedding owner information in a

multimedia object) and ﬁngerprinting (embedding

buyer information) have received signiﬁcant research

attention in the past decade. Since a multimedia ob-

ject is sold (usually) by one owner to multiple users,

each copy has the same watermark but a different ﬁn-

gerprint. Images, audio-visual and text documents,

software, and databases are general multimedia ob-

jects considered for watermarking. Images have been

the primary focus of research in watermarking (Bors

and Pitas, 1996; Braudaway, 1997; Cox et al., 1995;

Cox et al., 1997; Cox et al., 1996) due to two main

reasons. First, the human visual system (HVS) cannot

distinguish between images with minor differences,

and second, image pixels’ LSBs can be ﬂipped with-

out causing signiﬁcant distortion in the visual quality.

Database watermarking is a relatively new ﬁeld

which has seen contributions in the last ﬁve years.

A typical scenario requiring database watermarking

is when a company

C provides conﬁdential customer

data to an external organization O (eg. call center).

To ensure that O does not exploit the information

and doesn’t sell it, C embeds it’s watermark in the

database relation. Another application is in web ser-

vices, where data provider D makes a database rela-

tion available online for remote query. An attacker

may try to steal the relation using multiple “intel-

ligent” queries. To prevent this, D watermarks the

databases before making them available online using

a blind or non-blind watermarking scheme. In a blind

watermarking model, only the watermarked media

and a secret key are required to detect/extract water-

mark whereas in a non-blind watermarking scheme,

the unmarked multimedia object is also required in

addition to the watermarked copy and secret key. This

creates a situation where one needs to store the un-

marked object at a secondary secure location. In this

paper, we present a database watermarking scheme

that is reversible and semi-blind. We call the scheme

semi-blind because it does not require the original

database to detect watermark but the insertion algo-

rithm stores the original bits selected for modiﬁca-

tion as an embed trace

E T , which is input to the

detection algorithm. Size of E T is proportional to

283

Gupta G. and Pieprzyk J. (2007).

REVERSIBLE AND SEMI-BLIND RELATIONAL DATABASE WATERMARKING.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 279-286

DOI: 10.5220/0002136902790286

 SciTePress

the number of tuples being marked. Previous wa-

termarking schemes such as (Sion et al., 2004) have

also presented similar semi-blind watermarking mod-

els. Our scheme is an enhancement of the irreversible

watermarking model proposed by Agrawal and Kier-

nan (Agrawal and Kiernan, 2002). We show that sec-

ondary watermark attacks are feasible on (Agrawal

and Kiernan, 2002). Further, we modify the model to

eliminate this shortcoming and propose an additional

algorithm to achieve identify the rightful owner from

n contenders.

1.1 Organization of the Paper

Section 2 describes related work and provides a

detailed account of database watermarking from

(Agrawal and Kiernan, 2002) to eliminate shortcom-

ings. The modiﬁed algorithms are presented in Sec-

tion 4 and Section 5 contains their analysis. The pa-

per is concluded in Section 6 with a discussion on the

added advantages provided by the new scheme.

1.2 Notations Used

The following notations will be used through the pa-

per,

• R : Relation

• r : Tuple

• A

: i

attribute

• r.A

: i

attribute in tuple r

• A

: j

LSB of i

attribute

• r.A

: j

LSB of i

attribute in tuple r

• r.P : Primary key of tuple r

• ◦ : Concatenation

•

H () : One-way hash function

• R

ins(p)

−−−→ R

: R is watermarked by party p to be-

come relation R

, or in other words, a watermark

is inserted by party p into a document R resulting

in its watermarked version R

• R

det(p)

−−−→ R : R is restored when party p’s water-

mark is detected in R

• |x| : Size of x in bits

• abs(x) : Absolute value of x

• ⌊x⌋: Floor value of x

• Distance for attribute r.A

: δ

r.A

min

˜r6=r

{abs(r.A

− ˜r.A

)}

2 RELATED WORK AND

AGRAWAL-KIERNAN SCHEME

Several relational database watermarking models

have been proposed in (Agrawal and Kiernan, 2002;

Agrawal et al., 2003; Sion et al., 2004; Gross-

Amblard, 2003; Guo et al., 2006; Li and Deng, 2006;

Li et al., 2004; Zhang et al., 2004a; Zhang et al., 2006;

Zhang et al., 2004b). These schemes are irreversible

with the exception of (Zhang et al., 2006) and except

(Gross-Amblard, 2003), do not preserve queries. Ir-

reversible watermarking implies that the original re-

lation cannot be restored from the watermarked re-

lation. Ownership disputes might be unresolved if

an attacker successfully embeds a secondary water-

mark. But if the watermarking is reversible, the orig-

inal database can be restored and the correct owner

identiﬁed using suitable algorithm (discussed in sec-

tion 4.1).

The notions of local and global distortions are

presented in (Gross-Amblard, 2003) which achieve

the property of query-preservation. Local distortion

refers to the minimum difference between values of

an attribute. For formal deﬁnitions of local and global

distortions, please refer to (Gross-Amblard, 2003). In

a nutshell, the attributes should only be modiﬁed by a

value lesser than the local distortion.

Agrawal and Kiernan (Agrawal and Kiernan,

2002) were the ﬁrst to present a database watermark-

ing scheme that modiﬁes LSBs of numerical attributes

(selected using the private key and tuple’s primary key

value). This key-based attribute selection is common

to other proposals (Agrawal et al., 2003; Li and Deng,

2006).

2.1 Agrawal-Kiernan Scheme

The watermarking scheme consists of two algorithms;

Insertion, and Detection. The bits modiﬁed during

insertion are checked for correctness in the detection

algorithm for establishment of watermark presence.

Parameters to the insertion algorithm are,

• Database Relation R containing η tuples and υ

modiﬁable attributes {A

,...,A

}

• Number of modiﬁable LSBs ξ

• Fraction of tuples to be watermarked 1/γ

• Private key

The secret parameter set is given be φ =

(

K ,γ,υ,ξ). Algorithm 1 illustrates the watermark

insertion process. Tuples are selected using mes-

sage authentication code (MAC)

F (r.P) deﬁned as

H (K ◦ H (K ◦ (r.P)) (Schneier, 1996) and appropri-

ate bit in the tuple set to

H (K ◦ r.P)%2 till ω =

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

284

bits are marked. Converse procedure is applied on

the watermarked copy to detect the watermark (Al-

gorithm 2) by verifying the modiﬁed bit is equal

H (K ◦ ˜r

.P)%2. The primary key value is un-

changed. Parameters to the watermark detection algo-

rithm are watermarked database relation R

contain-

ing η tuples and υ attributes {A

,...,A

}, number

of LSBs modiﬁed ξ, fraction of tuples watermarked

1/γ, upper bound on probability of falsely detecting

watermark α, minimum number of correctly marked

attributes for successful detection τ, and private key

K .

Input: Relation R, private key K, fraction

LSB usage ξ

Output: Watermarked relation R

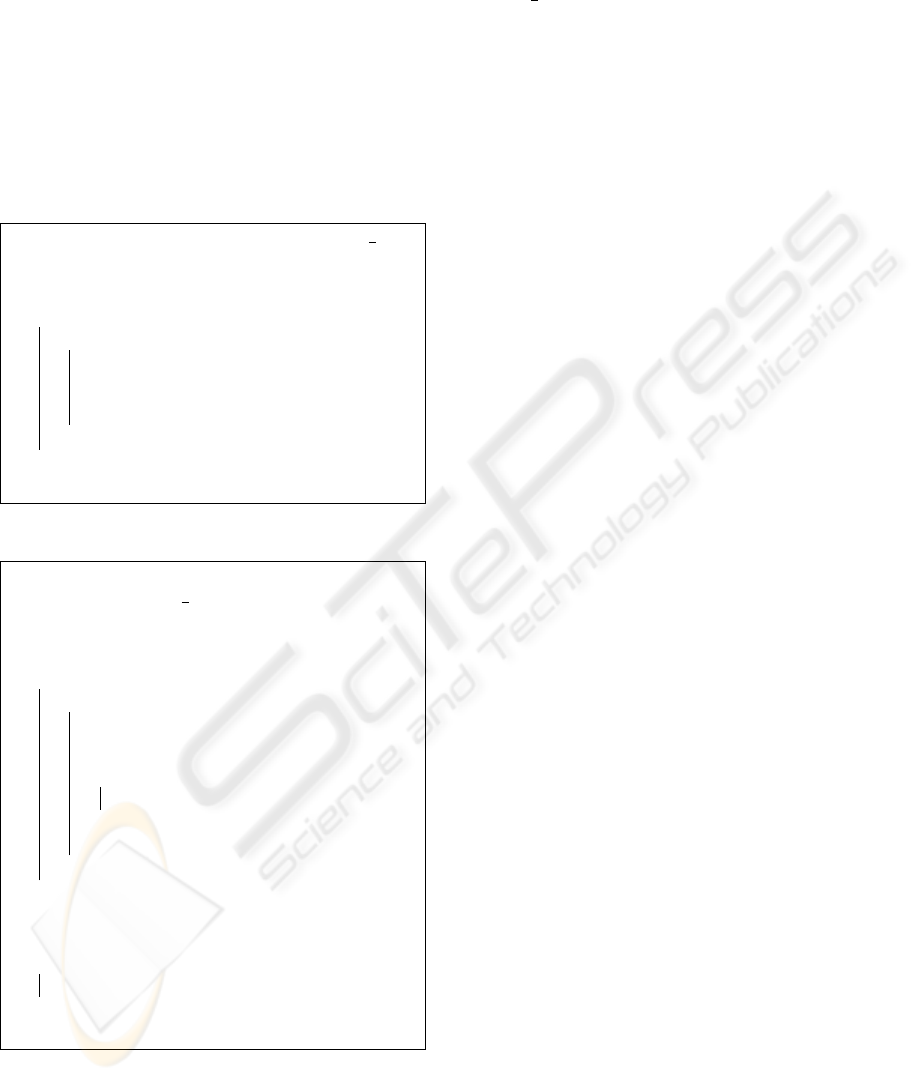
forall tuple r ∈ R do1

if F (r.P)%γ = 0 then2

i = F (r.P)%υ;3

j =

F (r.P)%ξ;4

r.A

H (K ◦ r.P)%2;5

end6

end7

return R;8

Algorithm 1: Agrawal-Kiernan watermark in-

sertion algorithm.

Input: Watermarked Relation

, private key

K, fraction

, LSB usage ξ

Output: Detection Status ∈ {true, false}

totalcount = matchcount = 0;1

forall tuple ˜r

∈

do2

if F (r.P)%γ = 0 then3

i = F (r.P)%υ;4

j =

F (r.P)%ξ;5

if ˜r

H (K ◦ ˜r

.P)%2 then6

matchcount = matchcount +1;7

end8

totalcount = totalcount + 1;9

end10

end11

τ = min{θ :

B (θ,totalcount,1/2) < α} ;

B12

defined in Equation 1

if matchcount ≥ τ then13

return true;14

end15

return f alse;16

Algorithm 2: Agrawal-Kiernan watermark de-

tection algorithm.

Equation 1 gives the binomial probability of hav-

ing at least k successes from n trials where probability

of success in a single trial is p. During detection, at

least τ bits need to be detected correctly in order to ex-

tract the correct watermark or in other words the prob-

ability of τ out of ω bits matching by sheer chance

B(τ,ω,

) should be less than the upper bound of false

positive α.

B (k, n, p) =

∑

i=k





(1− p)

n−i

(1)

2.2 Security Provided by

Agrawal-Kiernan Scheme

While discussing the security of the scheme, Agrawal

and Kiernan consider the following collection of at-

tacks,

A1: Bit attack: Updating some bits in numerical at-

tributes.

A2: Randomization attack: Assigning random values

to some bits.

A3: Rounding attack: Rounding off a ﬁxed number of

bits.

A4: Translation attack: Transforming numerical val-

ues to another data type.

A5: Subset attack: Removing a small subset of tuples/

attributes.

A6: Mix and match attack: Applying A4 on multiple

relations and merging them.

A7: Additive attack: Re-watermarking an already wa-

termarked relation.

A8: Invertibility attack: Checking if detection returns

true for a random key.

Inserting new tuples to destroy watermark will not

succeed as

F (r.P) identiﬁes marked tuple and two tu-

ples cannot have the same primary key. Success of

removing the watermark by deleting tuples depends

on the parameter γ. Probability of destroying water-

mark by deleting a few tuples is extremely low when

the fraction of tuples marked when γ is high. If γ is

high for a ﬁxed n, 1/γ is low and hence the fraction

of tuples marked are low. Thus the probability of the

attacker modifying the watermarked tuples is low. Bit

ﬂipping attacks (A1–A3) are probabilistically ineffec-

tive since the identiﬁcation of correct tuples, attributes

and LSBs is dependent on MAC. Additive and invert-

ibility attacks are still feasible.

REVERSIBLE AND SEMI-BLIND RELATIONAL DATABASE WATERMARKING

285

3 ANALYSIS OF

AGRAWAL-KIERNAN

WATERMARKING SCHEME

Based on our observations, Agrawal and Kiernan

scheme has three weaknesses.

1. Susceptibility of secondary watermarking:

Secondary watermarking refers to an attacker

who is trying to insert his watermark in an

already watermarked relation. The scheme does

not protect against secondary watermarking as

the attacker can choose his/her own parameter

list

φ and insert a new watermark in the original

watermarked relation. The new watermark will

establish the ownership of the attacker over

the relation and might also destroy the original

watermark. If the watermarking is reversible, the

actual owner’s watermark can be recovered from

the reversed relation.

2. Lack of query-preservation: If an attribute

r.A

= x

is modiﬁed to x

, then query “Select r

from R where r.A

= x

” cannot be preserved.

Thus, it is obvious that not all queries are preserv-

able in watermarked database. Distance δ

r.A

, that

refers to the minimum difference between value

of r.A

from values of A

in other tuples, is not

considered in (Agrawal and Kiernan, 2002), due

to which queries might not be preserved. If we

change value of an attribute beyond it’s distance,

the ordering of the tuples is modiﬁed when the

relation is sorted on that attribute and hence query

results change. Consider the following relations

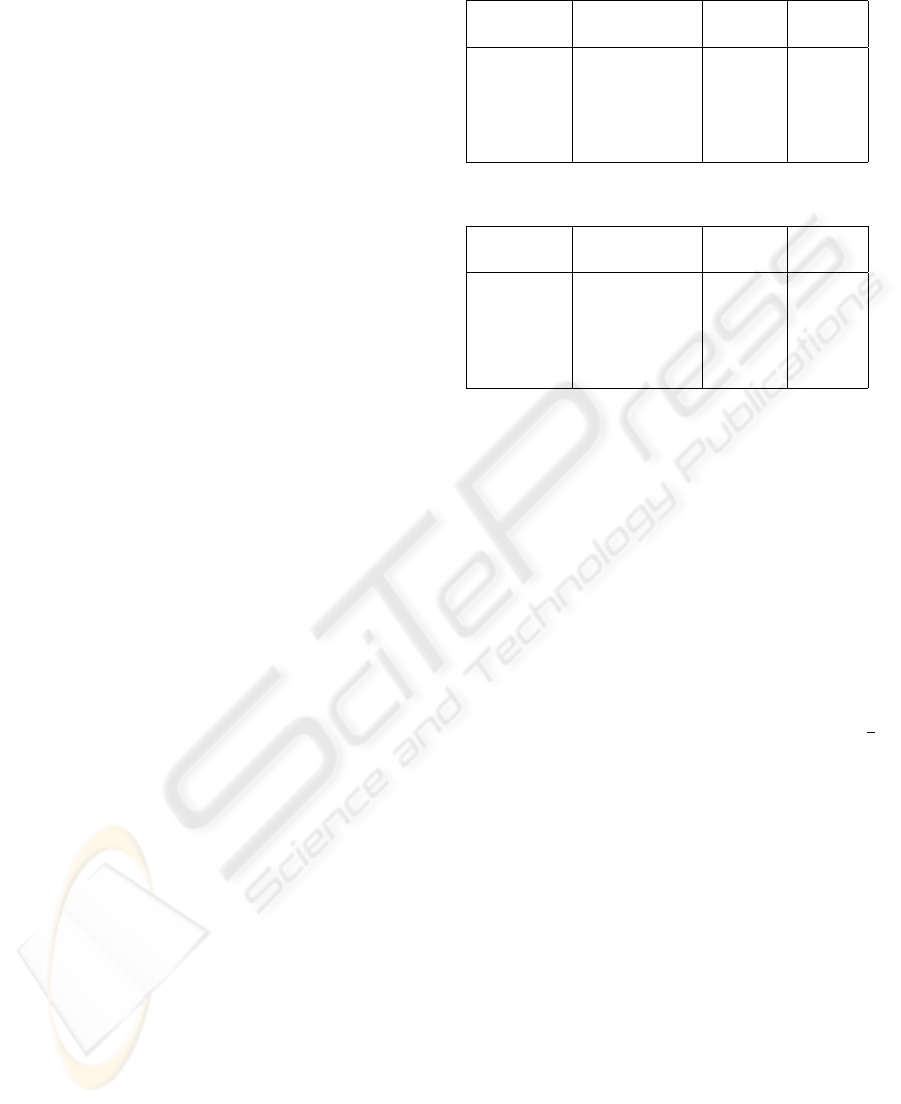
that contains foreign exchange rate data of some

countries against 100 US Dollars. Table 1 is the

original relation and Table 2 is the watermarked

relation.Result of queries “Select Nation from

ForEx where Selling rate<130” and “Select

Currency from ForEx where Buying rate is

maximum” are different when executed on the

original and watermarked relations.

3. Lack of tolerance of attributes: The number of

LSBs that can be used for watermarking are not

dependent on the tolerance of the attributes. This

results in the possibility that the relation becomes

unusable from a user’s perspective. Tolerance is

different from distance. For example, even if pop-

ulation of the two countries differ by millions,

modifying population values beyond a couple of

thousands might render the data useless. Hence,

the number of bits that one can change does not

depend only on distance, but also on tolerance.

Table 1: Original ForEx relation.

Currency Nation Buying Selling

code rate rate

AUD Australia 133 125

INR India 4500 4300

THB Thailand 3740 3510

SLR Sri Lanka 4430 4210

NZD New Zealand 151 134

Table 2: Watermarked ForEx relation.

Currency Nation Buying Selling

code rate rate

AUD Australia 133 125

INR India 4500 4300

THB Thailand 3740 3510

SLR Sri Lanka 4530 4310

NZD New Zealand 151 124

We propose the following modiﬁcations to eliminate

each of these weaknesses.

1. Secondary Watermarking

To defeat secondary watermarking attacks, the

step r.A

H (K ◦ r.P)%2 in Algorithm 1 is

changed to

E T = E T ◦ r.A

r.A

H (K ◦ r.P◦ r.A

)%2,

r.A

is concatenated to embed trace

E T and

then modiﬁed. The scheme is semi-blind and re-

versible, since the original values can be restored

from

E T . The size of E T is proportional to

At the detection time, the value of matchcount is

incremented only if

˜r

H (K ◦ ˜r

.P◦ E T [totalcount])%2

(i, j,totalcount,matchcount are counters updated

during the detection)

The owner stores

E T at a secondary location.

(

E T ,K ) is the watermark detection key. Sub-

section 4.1 discusses how the rightful owner is

identiﬁed if multiple parties watermark a relation

in some sequence. Implementation is given in

Algorithm 5.

2. Query preservation

The value of an attribute r.A

should be modi-

ﬁed by less than the distance δ

r.A

. Thereby, the

number of bits available for watermarking are

⌊log

(δ

r.A

)⌋ (For example, if the smallest differ-

ence between values of an attribute in two rows is

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

286

57.68, then only 5 bits can be used for watermark-

ing as log

(57.68) = 5.85 and ⌊5.85⌋ = 5). This

would guarantee query-preservation for the exist-

ing relation. Since the watermarking scheme is re-

versible, it facilitates incremental watermarking.

The steps involved in incremental watermarking

are,

(a) Restore relation to unmarked version.

(b) Add (or delete) required tuples (or attributes).

3. Tolerance

Since each attribute has a different tolerance limit

beyond which it should not be modiﬁed, it is rec-

ommended that the number of LSBs to utilize

for watermarking should be a function of toler-

ance of the attributes. Hence, ξ

LSBs of attribute

can be modiﬁed. The list of all these values

Ξ = {ξ

,ξ

,...,ξ

} where υ attributes are avail-

able for watermarking.

4 MODIFIED ALGORITHMS

With the above modiﬁcations, the secret param-

eter list for watermark detection becomes φ =

(

K ,E T , γ, υ, Ξ). We present a reversible and

semi-blind watermarking scheme that comprises

of three algorithms; Insertion, Detection, and

(1,n)identification. The algorithms are presented

in Algorithm 3, Algorithm 4, and Algorithm 5 re-

spectively. They contain comments illustrating the

purpose served by various steps. The acronym WM

refers to “watermark” in the three algorithms.

4.1 Identifying Rightful Owner

In this additional algorithm, ownership disputes can

be resolved through backtracking. If R

ins(p

)

−−−−→ R

followed by R

ins(p

)

−−−−→ R

, then R

det(p

)

−−−−→ R

will

show that the restored relation R

has already been

watermarked by another party (p

) and hence p

not the original owner. For all potential owners u

we compare relations restored R

restored

after detect-

ing watermark of party u

, and if it matches any other

party’s watermarked relation R

within a preset tol-

erance limit ε, then u

is eliminated from the list of

possible owners. Each party supplies its secret pa-

rameter list φ. and the relation R

on which it claims

ownership. A limitation is that each party that has wa-

termarked the relation should participate in the owner-

identiﬁcation process. If this condition is not satisﬁed,

we might not be able to associate the restored relation

with another user, in which case the algorithm will

fail.

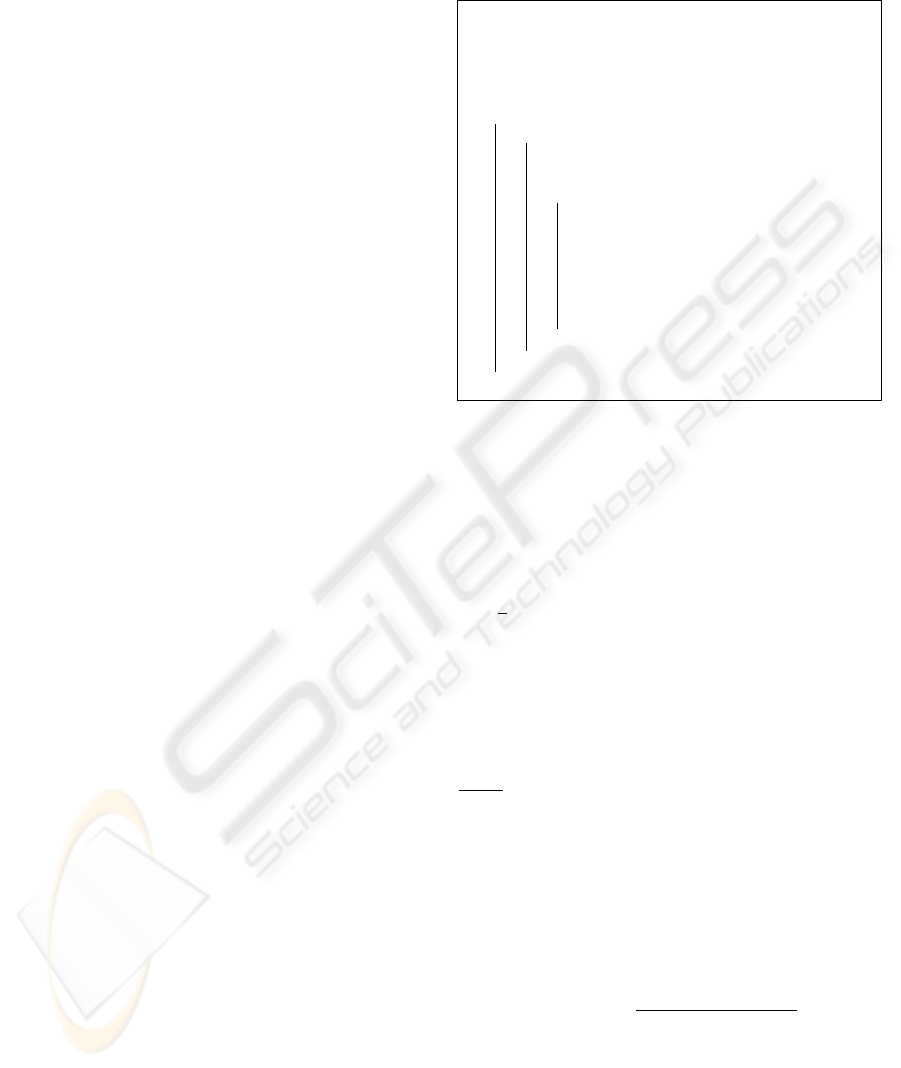
Input: Relation R, private key K, fraction γ, number of

markable attributes υ, LSB usage

Ξ = {ξ

,ξ

,. .. ,ξ

}

Output: Watermarked relation R

, Embed Trace E T

count = 0 ;

// index in WM to be generated

forall tuples r ∈ R do2

if F (r.P)%γ = 0 then3

i = F (r.P)%υ;

// identify attribute

j = F (r.P)%ξ

;

// identify bit

if j < ⌊log

(δ

r.A

)⌋ then6

E T [count] = r.A

;

// store old value

in WM

count = count + 1;

// next watermark

bit’s index

r.A

= H (K ◦ r.P ◦ r.A

)%2 ;

// modify

bit in relation

end10

end11

end12

Algorithm 3: Watermark insertion.

5 ANALYSIS

According to (Agrawal and Kiernan, 2002), the at-

tacker Mallory needs to ﬂip at least

τ = ω − τ + 1

marked bits to carry out a successful attack, where

ω =

. Let us assume that Mallory somehow knows

the values of ξ and υ and randomly chooses ζ tuples.

The probability that this attack will succeed when

Mallory ﬂips A

for all υ attributes in all randomly

selected ζ tuples is given in Equation 2 (Agrawal and

Kiernan, 2002), and the values are provided in Ta-

ble 3. For our modiﬁed watermarked scheme, ξ =

∑

i=1

. Note that if the attacker ﬂips more than 50%

bits, the watermark will be detected when the entire

bits in the relation are ﬂipped. This also gives us a

fair idea about the value of γ that should be chosen.

It should be fairly low and somewhere in between 10

and 100 as the attack is ineffective for values in this

range.

P (A ) =

∑





η− ω

ζ− i







(2)

Without the knowledge of ξ,γ,υ, Mallory’s task is

much tougher. To compensate for the lack of knowl-

edge, Mallory might need to choose an estimated

′

and ﬂip that bit of each of the attribute which

degenerates the data quality. The security analysis

REVERSIBLE AND SEMI-BLIND RELATIONAL DATABASE WATERMARKING

287

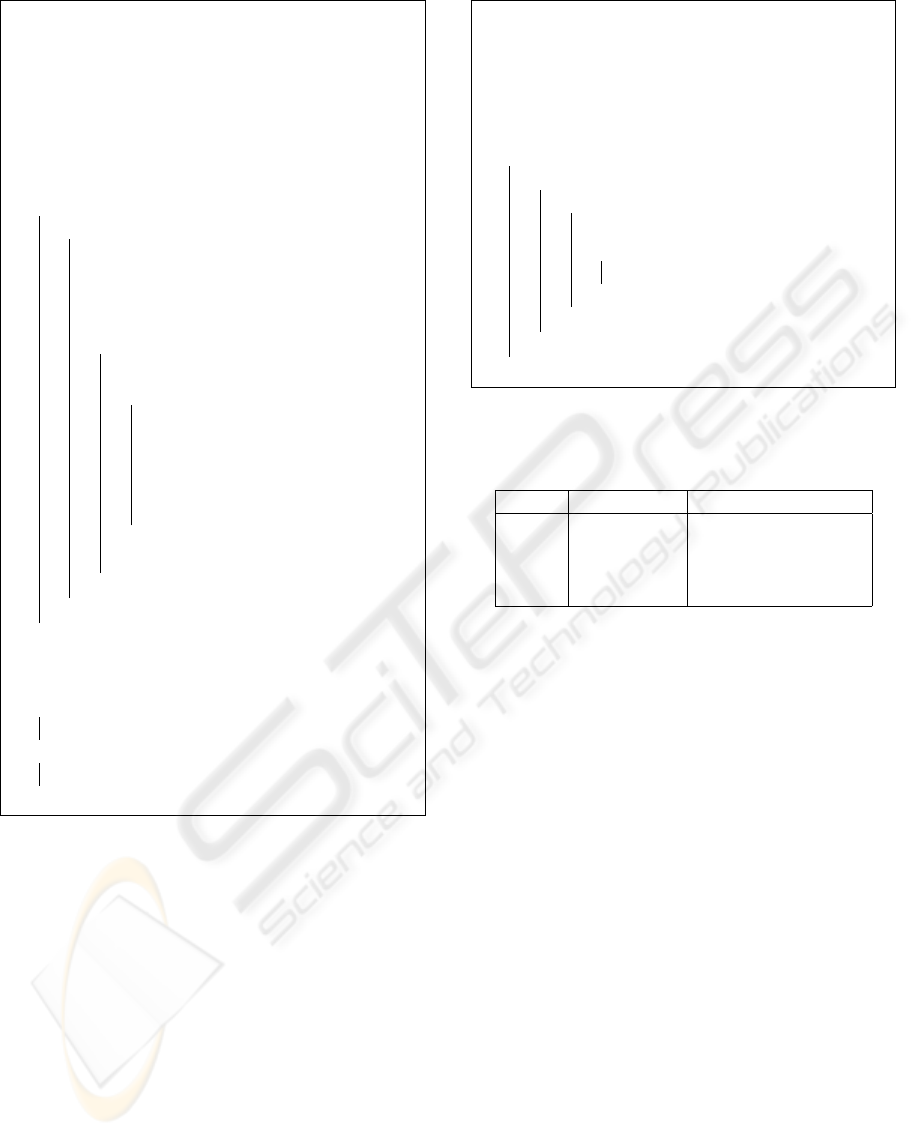
Input: Watermarked Relation

, Secret

parameter list φ = (

K ,E T , γ, υ, Ξ)

Output: {Watermark Status ∈ {true, false},

Restored Relation R}

R =

matchcount = 0 ;

// matching WM bits

counter

totalcount = 0 ;

// total WM bits counter

forall tuples ˜r

∈

do4

if F (r.P)%γ = 0 then5

i = F (r.P)%υ;

// identify marked

attribute

j = F (r.P)%ξ

;

// identify marked

bit

if j < ⌊log

(δ

r.A

)⌋ then8

if H (K ◦ ˜r

.P) ⊕9

E T [totalcount]%2 = ˜r

then

matchcount = matchcount +1;10

// bit authenticated

r.A

= E T [totalcount];11

// restore bit in

relation

end12

totalcount = totalcount + 1;13

end14

end15

end16

τ = min(θ) : B(θ,totalcount,1/2) < α;17

// threshold check

if matchcount ≥ τ then18

return {true,R};19

else20

return { false,

};21

end22

Algorithm 4: Watermark detection.

for (Agrawal and Kiernan, 2002) also holds for our

scheme as the underlying operations are retained.

The advantages of our reversible watermarking

scheme as compared to (Agrawal and Kiernan, 2002)

are,

1. Ownership resolution amongst n parties

This is not possible in the absence of a reversible

watermarking scheme. Consider a situation in

Figure 1 where a company C and ﬁve data servers

are contesting for ownership over

a relation, each party having a slightly different

version of the same relation. The dotted line

represents a relation being distorted by a party

in an attempt to destroy any watermark it con-

Input: Potential owners U = {u

,...,u

Secret parameter list of each u

= {

E T

,γ

,υ

,Ξ

}, tolerance ε,

Potential owners’ versions of the

watermarked relation {

,...,

}

Output: Owner O

forall u

∈

U do1

if detect(

) == {true,R

′

} then2

forall u

∈ U do3

if (difference(

′

) < ε) OR4

(detect(R

′

) == true) then

U = U \ u

end6

end7

end8

end9

Algorithm 5: (1,n)identification.

Table 3: Probability of success for bit ﬂipping attack.

γ bits ﬂipped success probability

10000 40% 0.64

1000 46% 0.44

100 48% 0.11

10 >50% ≈ 0

tains. We assume that γ < 100 for all the par-

ties who have watermarked the relation, which

gives a high probability of the watermark be-

ing preserved if the relation is distorted or re-

watermarked (Table 3). Hence, C’s watermark is

also detected in

and d

’s watermark is also

detected in

. When we execute Algo-

rithm 5, the relation restored upon detecting wa-

termark of each party matches another party’s re-

lation (except when C’s watermark is detected).

For example, the relation

restored upon detect-

ing d

’s watermark in R

matches R

within tol-

erance limit ε. But the relation R restored upon

detecting the watermark of the authentic owner C,

does not match any other party’s relation, which

establishes C’s ownership.

Line 4 of Algorithm 5 maximizes the probability

of identifying if the restored relation has been pre-

viously marked by another party. If the attacker

only slightly modiﬁes the relation before water-

marking, the value of difference(

′

) is less

than ε, and even if the attacker changes the rela-

tion extensively, the value of detect(R

′

) is true

with a high probability (by Equation 2).

If some of the parties do not participate in the

owner identiﬁcation process, the algorithm might

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

288

fail. If we model parties watermarking relations as

nodes of a tree where the actual owner is the root

of the tree, then the probabilities with which the

owner will be correctly identiﬁed despite nodes

from n levels of the tree abstaining from participa-

tion is given by (1−

P (A ))

. These probabilities

are calculated taking into consideration the mod-

iﬁcations the attacker might make in the relation

before watermarking it. The probability that an

attacker will succeed in destroying the watermark

P (A ) and hence the probability of the relation

surviving an attack is 1 −

P (A ). The probabil-

ity of a relation surviving n sequential attacks is

(1 − P (A ))

. It is extremely rare that the rela-

tion will be distributed beyond three or four lev-

els as there usually a few companies dealing with

similar data. It is shown in (Agrawal and Kier-

nan, 2002) that the attacker has a probability of

11% success if he changes 48% of the tuples as-

suming γ = 100. Hence, if only C and d

par-

ticipate in the correct algorithm, C will be iden-

tiﬁed as the correct owner with a probability of

89% since parties from only one level (d

) ab-

stain. This probability is 100% if C,d

partici-

pate or C,d

participate. In general, successful

detection of the correct watermark occurs with the

probability of 0.89

where n levels abstain from

participation for γ = 100. Thus the probability

of ﬁnding rightful owner if two levels abstain is

0.89∗ 0.89 = 0.7921.

insert(C)



insert(d

)



insert(d

)



insert(d

)



insert(d

)



insert(d

)



Figure 1: Dotted lines denote relation manipulated and

solid lines denote relation watermarked.

2. Situations requiring original dataset

Often, companies require precise data where a dif-

ference of even one bit might be disastrous such

as stock markets and military operations. Once

a relation is watermarked in (Agrawal and Kier-

nan, 2002), it cannot be restored to it’s original

state if needed. Since our watermarking scheme

is reversible, the original data can be restored by

executing the detection algorithm. It is also possi-

ble to distribute low-quality data free of cost and

users can then purchase the key to extract original

data.

5.1 Semi-blindness

As mentioned in the introduction, the two alter-

natives to facilitate reversibility are 1) Store orig-

inal bits at a secondary location before modifying

(This is the implemented solution in our paper or

2) Original bits and watermark bits should be re-

coverable from modiﬁed bits.

There are a few ways of implementing the second

option,

Algorithm 3, statement 9 can be replaced by

r.A

H (K ◦ r.P) ⊕ r.A

%2. But an attacker

A can run the insertion algorithm with inputs

′

,γ

′

,υ

′

,Ξ

′

) and get output R

′

such that

′

ins(A )

−−−→ R

. Also R

ins(C )

−−−→ R

, thus making it

impossible to decide who (owner/ attacker) wa-

termarked the relation ﬁrst. Thus the this solution

is vulnerable to pre-image attacks.

There have been reversible watermarking algo-

rithms, primarily for images (Alattar, 2004; Tian,

2003). These schemes facilitate watermarking by

encoding watermark bit and original value in the

modiﬁed value at at the cost of watermarking ca-

pacity. Another option is to use lossless compres-

sion to ﬁrst compress the original bits, append wa-

termark bits and embed resulting bitstream (Celik

et al., 2002). Since lossless compressions are sen-

sitive to modiﬁcations, such schemes are not very

resilient as suggested in (Jen-Bang Feng and Chu,

2006).

The ﬁrst challenge in designing a blind reversible

scheme for database relations is that lossless com-

pression technique is not resilient against attacks.

The second problem is that adapting reversible

image watermarking schemes is harder because

neighboring attributes or tuples do not have cor-

relation unlike images, which is a prerequisite

for schemes such as (Alattar, 2004). Our next

research endeavor is to implement a fully blind

REVERSIBLE AND SEMI-BLIND RELATIONAL DATABASE WATERMARKING

289

database watermarking model by working around

these two limitations.

6 CONCLUSION

The watermarking scheme proposed by Agrawal and

Kiernan is irreversible, resulting in problems during

owner identiﬁcation in case of additive or secondary

watermarking attacks. Our modiﬁed scheme is re-

versible and thus the rightful owner can be identiﬁed

from n candidates. The major advantages of our pro-

posed scheme are 1)It provides query preservation, 2)

It identiﬁes rightful owner if relation is watermarked

by multiple parties, and 3) It facilitates reversibility.

The current model requires modiﬁed bits to be

stored at a secondary location (

E T ). Our future re-

search is directed towards eliminating this require-

ment and formulate a reversible blind watermarking

scheme. The second enhancement is watermarking

relations that do not contain a primary key. Concate-

nated attributes in a tuple can act as a primary key

in such cases. However, the possibility of duplicate

attributes makes identiﬁcation of marked tuples difﬁ-

cult. One possibility is to treat tuples with duplicate

attributes as a single tuple.

REFERENCES

Agrawal, R., Haas, P. J., and Kiernan, J. (2003). Water-

marking relational data: framework, algorithms and

analysis. The VLDB Journal, 12(2):157–169.

Agrawal, R. and Kiernan, J. (2002). Watermarking rela-

tional databases. In Proceedings of the 28th Interna-

tional Conference on Very Large Databases VLDB.

Alattar, A. (2004). Reversible watermark using the dif-

ference expansion of a generalized integer transform.

IEEE Transactions on Image Processing, 13(8):1147–

1156.

Bors, A. and Pitas, I. (1996). Image watermarking using

dct domain constraints. In Proceedings of IEEE Inter-

national Conference on Image Processing (ICIP’96),

volume III, pages 231–234.

Braudaway, G. W. (1997). Protecting publicly-available im-

ages with an invisible image watermark. In Proceed-

ings of IEEE International Conference on Image Pro-

cessing (ICIP’97), Santa Barbara, California.

Celik, M. U., Sharma, G., Tekalp, M. A., and Saber, E.

(2002). Reversible data hiding. In Proceedings of

International Conference on Image Processing, vol-

ume 2, pages 157–160.

Cox, I., Kilian, J., Leighton, T., and Shamoon, T. (1995).

Secure spread spectrum watermarking for multimedia.

Technical Report 128, NEC Research Institute.

Cox, I., Kilian, J., Leighton, T., and Shamoon, T. (1997).

Secure spread spectrum watermarking for multimedia.

IEEE Transactions on Image Processing, 6(12):1673–

1687.

Cox, I. J., Killian, J., Leighton, T., and Shamoon, T. (1996).

Secure spread spectrum watermarking for images, au-

dio, and video. In IEEE International Conference on

Image Processing (ICIP’96), volume III, pages 243–

246.

Gross-Amblard, D. (2003). Query-preserving watermark-

ing of relational databases and xml documents. In

Proceedings of the 20th ACM Symposium on Princi-

ples of Database Systems, pages 191–201.

Guo, F., Wang, J., and Li, D. (2006). Fingerprinting rela-

tional databases. In SAC ’06: Proceedings of the 2006

ACM symposium on Applied computing, pages 487–

492, New York, NY, USA. ACM Press.

Jen-Bang Feng, Iuon-Chang Lin, C.-S. T. and Chu, Y.-P.

(2006). Reversible watermarking: Current status and

key issues. International Journal of Network Security,

2(3):161–171.

Li, Y. and Deng, R. H. (2006). Publicly veriﬁable ownership

protection for relational databases. In Proceedings of

the ACM Symposium on Information, computer and

communications security, pages 78–89, New York,

NY, USA. ACM Press.

Li, Y., Guo, H., and Jajodia, S. (2004). Tamper detection

and localization for categorical data using fragile wa-

termarks. In DRM ’04: Proceedings of the 4th ACM

workshop on Digital rights management, pages 73–

82, New York, NY, USA. ACM Press.

Schneier, B. (1996). Applied Cryptography. John Wiley,

second edition.

Sion, R., Atallah, M., and Prabhakar, S. (2004). Rights

protection for relational data. IEEE Transactions

on Knowledge and Data Engineering, 16(12):1509–

1525.

Tian, J. (2003). Reversible data embedding using a differ-

ence expansion. IEEE Transactions on Circuits and

Systems for Video Technology, 13(8):890–896.

Zhang, Y., Niu, X.-M., and Zhao, D. (2004a). A method

of protecting relational databases copyright with cloud

watermark. Transactions of Engineering, Computing

and Technology, 3:170–174.

Zhang, Y., Yang, B., and Niu, X.-M. (2006). Reversible

watermarking for relational database authentication.

Journal of Computers, 17(2):59–66.

Zhang, Z. H., Jin, X. M., Wang, J. M., and Li, D. Y. (2004b).

Watermarking relational database using image. In

Proceedings of 3rd International Conference on Ma-

chine Learning and Cybernetics, volume 3, pages

1739–1744.

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

290