
FUSION PREDICTORS FOR DISCRETE-TIME LINEAR
SYSTEMS WITH MULTISENSOR ENVIRONMENT
Ha Ryong Song and Vladimir Shin
Department of Mechatronics, Gwangju Institute of Science and Technology
1 Oryong-Dong, Buk-Gu, Gwangju, 500-712, South Korea
Keywords: Discrete-time linear system, Kalman predictor, fusion formula, multisensor.
Abstract: New fusion predictors for linear dynamic systems with different types of observations are proposed. The
fusion predictors are formed by summing of the local Kalman filters/predictors with matrix weights
depending only on time instants. The relationship between them and the optimal predictor is discussed. High
accuracy and computational efficiency of the fusion predictors are demonstrated on the first-order Markov
process and the damper harmonic oscillator motion with multisensor environment.
1 INTRODUCTION
The integration and fusion of information from a
combination of different types of observed
instruments (sensors) are often used in the design of
high-accuracy control systems. Typical applications
that can benefit, the use of multiple sensors, are
industrial tasks, military command, mobile robot
navigation, multi-target tracking, and aircraft
navigation (see Hall, 1992; Bar-Shalom and Li,
1995). If it is decided that all local sensors observe
the same target, then the next problem is how to
combine the correspondence local estimates.
Several distributed fusion architectures were
discussed in Bar-Shalom (1990) and Bar-Shalom
and Campo (1986) and Li et al. (2004) and
algorithms for distributed estimation fusion have
been developed in Bar-Shalom and Campo (1986)
and Shin et al. (2004, 2006) and Zhou et al. (2006).
The Bar-Shalom and Campo fusion formula (FF) for
two-sensors systems has been generalized for an
arbitrary number of sensors in Shin et al. (2004,
2006). FF represents an optimal mean-square linear
combination of the local estimates with the matrix
weights satisfying the linear algebraic equations.
The explicit expression for the matrix weights has
been derived in Zhou et al. (2006). Application of
FF to some estimation and filtering problems was
proposed in Bar-Shalom and Campo (1986), Li et
al. (2004), and Shin et al. (2004, 2006). The main
purpose of this paper is development of fusion
predictors to forecast the future state of the linear
multisensor systems.
This paper is organized as follows. In Section 2,
we present the statement of the prediction problem
with multisensor environment and give its optimal
solution. In Section 3, we propose two fusion
predictors, which are derived by using the FF. In
Section 4, the fusion predictors are tested and
compared. Finally, Section 5 is the conclusion.
2 STATEMENT OF PROBLEM
KALMAN PREDICTOR
Consider a discrete-time linear dynamic system with
additive white Gaussian noise,
,0,1,k,vGxFx
kkkk1k
K=
+
=
+
(1)
where
n
k
x ℜ∈
is state vector, and
r
k
v ℜ∈
is white
Gaussian noise,
(
)
kk
Q0,N~v
.
Suppose that overall observation vector
m
k
Y ℜ∈
is composed of
N
different types of observation
subvectors (local sensors)
(N)
k
(1)
k
y,,y K
,
[
]
,yyY
T
(N)
k
(1)
kk
TT
L=
(2)
where
(i)
k
y
are determined by the equations
,y,wxHy
,y,wxHy
N
1
m
(N)
k
(N)
kk
(N)
k
(N)
k
m
(1)
k
(1)
kk
(1)
k
(1)
k
ℜ∈+=
ℜ∈+=
M
(3)
119
Ryong Song H. and Shin V. (2007).
FUSION PREDICTORS FOR DISCRETE-TIME LINEAR SYSTEMS WITH MULTISENSOR ENVIRONMENT.
In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 119-124
DOI: 10.5220/0002131201190124
Copyright
c
SciTePress

where
(N)
k
(1)
k
w,,w K
are white Gaussian noises,
(
)
(i)
k
(i)
k
R0,~w N
,
mmm
N1
=++L
. The initial state is
modeled as a Gaussian random vector,
(
)
000
P,x~x N
.
The system and observation noises
k
v
and
,N1,...,i,w
(i)
k
=
and the initial state
0
x
are mutually
uncorrelated.
Prediction (or fixed-lead prediction) is the
estimation of the state at future time
0s,sk ≥+
beyond the observation interval, that is, based on
data up to an earlier time
k
,
(
)
{}
.k0,...,i,YY,YxEx
ˆ
ik][0,k][0,sk
ksk
===
+
+
(4)
The Kalman predictor (KP). The optimal predictor
KP
kskksk
x
ˆ
x
ˆ
++
≡
and its error covariance
KP
kskksk
PP
++
≡
are
given by the Kalman predictor equations:
,1,2,...s,GQGQ
~
,Q
~
FPFP
,x
ˆ
Fx
ˆ
T
1sk1sk1sk1-sk
1sk
T
1sk
KP
k1-sk
1sk
KP
ksk
KP
k1-sk
1sk
KP
ksk
==
+=
=
−+−+−++
−+−+
+
−+
+
+
−+
+
(5)
with initial conditions
KP
kk
KP
kk
P,x
ˆ
determined by the
standard Kalman filter (KF) equations(Bar-Shalom
et al. 2001, Lewis 1981). Note that the optimal
predictor
KP
ksk
x
ˆ
+
represents the centralized predictor,
which processing the
overall observations
k][0,
Y
simultaneously.
Many advanced systems now make use of a large
number of sensors in practical applications ranging
from aerospace and defense, robotics automation
systems, to the monitoring and control of process
generation plants. Recent developments in integrated
sensor network systems have further motivated the
search for decentralized signal processing algorithms.
An important practical problem in the above systems
is to find a fusion estimate to combine the
information from various local estimates to produce
a global (fusion) estimate.
In next Section, we propose two new fusion
predictors for multisensor discrete-time dynamic
systems (1), (3).
3 TWO FUSION PREDICTORS
The derivation of the fusion predictors is based on
the assumption that the
overall observation vector
k
Y
combines the local (individual) sensors
(N)
k
(1)
k
y,,y K
, which can be processed separately.
According to (1) and (3), we have
N
unconnected
dynamic subsystems (
N,1,i K
=
) with the state
k
x
and local sensor
(i)
k
y
:
,wxHy
,vGxFx
(i)
kk
(i)
k
(i)
k
kkkk1k
+=
+
=
+
(6)
where
i
is the fixed-number of subsystem. Then the
optimal mean-square local filtering
(
)
(i)
k][0,k
(i)
kk
yxEx
ˆ
=
and prediction
(
)
(i)
k][0,sk
(i)
ksk
yxEx
ˆ
+
+
=
estimates are
determined by the recursive Kalman filtering
equations,
{
}
k0,...,j,yy
(i)
j
(i)
k][0,
==
(Bar-Shalom et al.
2001). We have
,Q
~
FPFP
,,...2,1s,x
ˆ
Fx
ˆ
1sk
T
1sk
(ii)
k1-sk
1sk
(ii)
ksk
(i)
k1-sk
1sk
(i)
ksk
−+−+
+
−+
+
+
−+
+
+=
==
(7)
[]
[]
[]
,PHLIP
,RHPHHPL
,PP,Q
~
FPFP
,x
ˆ
HyLx
ˆ
x
ˆ
,xx
ˆ
,x
ˆ
Fx
ˆ
(ii)
k1k
(i)
1k
(i)
1kn
(ii)
1k1k
1
(i)
1k
(i)
1k
(ii)
k1k
(i)
1k
(i)
1k
(ii)
k1k
(i)
1k
0
(ii)
00
k
T
k
(ii)
kk
k
(ii)
k1k
(i)
k1k
(i)
k
(i)
k
(i)
1k
(i)
k1k
(i)
1k1k
0
00kk
k
k1k
TT
+
++
++
−
++
+
++
+
+
+
+
+
+++
+
−=
+=
=+=
−+=
=
=
(8)
where
n
I
is an
nn
×
identity matrix, and
(ii)
kk
P
and
(ii)
ksk
P
+
are the filtering and prediction local error
covariances, respectively, i.e.,
(
)
..0,1,2,..j,x
ˆ
xx
~
,x
~
,x
~
covP
(i)
kjk
jk
(i)
kjk
(i)
kjk
(i)
kjk
(ii)
kjk
=−=
=
+
+
+
+++
(9)
Thus we have
N
local Kalman estimates
,x
ˆ
,x
ˆ
(i)
ksk
(i)
kk +
and the corresponding error
covariances
(i)
ksk
(i)
kk
P,P
+
for
N.1,...,i =
Using these
local estimates and covariances we propose two
fusion prediction algorithms.
3.1 The Fusion of Local Predictors
(FLP Algorithm)
The fusion predictor
FLP
ksk
x
ˆ
+
of the state
sk
x
+
based on
the overall sensors (2) is constructed from the local
predictors
(i)
ksk
x
ˆ
+
by using FF (Shin et al. 2004, 2006
and Zhou et al. 2006):
,Ia,x
ˆ
ax
ˆ
n
N
1i
(i)
sk,
N
1i
(i)
ksk
(i)
sk,
FLP
ksk
==
∑∑
==
+
+
(10)
where
(N)
sk,
(1)
sk,
a,,a K
are
nn
×
time-varying matrix
weights determined from the mean-square criterion,
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
120

.minx
ˆ
a-xEJ
(i)
sk,
a
2
N
1i
(i)
ksk
(i)
sk,sk
FLP
ksk
→
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑
=
+
+
+
(11)
The following Theorem and Corollary completely
define the fusion predictor
FLP
ksk
x
ˆ
+
and its error
covariance,
(
)
FLP
ksk
FLP
ksk
FLP
ksk
x
~
,x
~
covP
+++
=
.
Theorem: Let
(N)
ksk
(1)
ksk
x
ˆ
,,x
ˆ
++
K
are the local Kalman
predictors of an unknown state
sk
x
+
. Then
(a) The weights
(N)
sk,
(1)
sk,
a,,a K
satisfy the linear
algebraic equations
[]
,Ia,0PPa
n
N
1i
(i)
sk,
N
1i
(iN)
ksk
(ij)
ksk
(i)
sk,
==−
∑∑
==
++
(12)
and they can be explicitly written out in the
following form
()
;N1,...,i,PPa
1
N
1h,
1)(
h)(
ksk
N
1j
)1(
(ij)
ksk
(i)
sk,
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
=
−
+
=
−
+
∑∑
l
l
(13)
(b) The local cross-covariances
(
)
jiN;1,...,ji,,x
~
,x
~
covP
(j)
ksk
(i)
ksk
(ij)
ksk
≠==
+++
(14)
satisfy the following recursions:
,.1,2,..s,Q
~
FPFP
1sk
T
1sk
(ij)
k1sk
1sk
(ij)
ksk
=+=
−+−+
−+
−+
+
(15)
()
(
)
()
0
(ij)
00
T
(j)
k
(j)
kn
1k
T
1k
(ij)
1k1k
1k
(i)
k
(i)
kn
(ij)
kk
PP,HLI
Q
~
FPFHLIP
=−×
+⋅−=
−−
−−
−
(16)
with the gains
(i)
k
L
determined by (8).
(c) The fusion error covariance
FLP
ksk
P
+
is given by
.aPaP
N
1ji,
(j)
sk,
(ij)
ksk
(i)
sk,
FLP
ksk
T
∑
=
++
=
(17)
Corollary: If
(N)
ksk
(1)
ksk
x
ˆ
,,x
ˆ
++
K
are unbiased local
Kalman estimates then the fusion predictor
FLP
ksk
x
ˆ
+
in
(10) is unbiased
.
The proofs of Theorem and Corollary are given in
Appendix.
Thus the local Kalman filtering estimates (8), and
the recursive fusion equations (10)-(17) completely
define FLP algorithm.
In particular case at
2N
=
, FF (10)-(13) reduces
to the Bar-Shalom and Campo formula:
()
()
.PPPPD
,DPPa
,DPPa
,x
ˆ
ax
ˆ
ax
ˆ
(21)
ksk
(12)
ksk
(22)
ksk
(11)
ksk
sk,
1
sk,
(12)
ksk
(11)
ksk
(2)
sk,
1
sk,
(21)
ksk
(22)
ksk
(1)
sk,
(2)
ksk
(2)
sk,
(1)
ksk
(1)
sk,
FLP
ksk
++++
−
++
−
++
++
+
−−+=
−=
−=
+=
(18)
Further, in parallel with FLP we offer the other
algorithm for fusion prediction.
3.2 The Prediction of Fusion Filter
(PFF Algorithm)
This algorithm consists of two parts. The first part
fuses the local Kalman filtering estimates
(N)
kk
(1)
kk
x
ˆ
,...,x
ˆ
using FF. We have
,Ib,x
ˆ
bx
ˆ
n
N
1i
(i)
k
N
1i
(i)
kk
(i)
k
FF
kk
==
∑∑
==
(19)
where the weights
(N)
k
(1)
k
b,,b K
satisfy the linear
algebraic equations (Shin et al. 2006)
[
]
,Ib,0PPb
n
N
1i
(i)
k
N
1i
(iN)
kk
(ij)
kk
(i)
k
==−
∑∑
==
(20)
or explicitly expressed from the formula (Zhou et al.
2006):
()
;N1,...,i,PPb
1
N
1h,
1)(
h)(
kk
N
1j
)1(
(ij)
kk
(i)
k
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
=
−
=
−
∑∑
l
l
(21)
where the local cross-covariances
(ij)
kk
P
are
determined by (8) and (16).
In the second part we predict the fusion filtering
estimate
FF
kk
x
ˆ
using one-step prediction:
.x
ˆ
x
ˆ
,FA,x
ˆ
A
x
ˆ
FFx
ˆ
Fx
ˆ
FF
kk
PFF
kk
1s
0j
j1sksk,
FF
kk
sk,
PFF
k2sk
2sk1sk
PFF
k1sk
1sk
PFF
ksk
≡==
===
∏
−
=
−−+
−+
−+−+
−+
−+
+
L
(22)
Remark 1 (Estimation accuracy): Experimentally,
FLP and PFF have very close accuracy, as in Section
4. Unfortunately, now we do not have a rigorous
proof or disproof of this result.
Remark 2 (Computational complexity): In general,
the both results, namely, linear equations (12), (20)
and expressions (13),(21) are equivalent, being the
implicit and explicit forms of the solution,
respectively. However, from the computational point
of view, when the number of sensors
N
is large or
the local cross-covariance matrices
(ij)
ksk
P
+
are ill-
conditioned, the linear equations may be more
preferable than the explicit expressions.
To predict the state
sk
x
+
using the FLP we need
to compute the matrix weights
(N)
jk,
(1)
jk,
a...,,a
for each
FUSION PREDICTORS FOR DISCRETE-TIME LINEAR SYSTEMS WITH MULTISENSOR ENVIRONMENT
121

lead
s1,2,...,j =
in contrast to the PFF, wherein the
weights
(N)
k
(1)
k
b...,,b
are computed only once, since
they do not depend on the leads
1.s ≥
Therefore the
FLP is more complex than the PFF, especially for
the large leads
1.s >>
Remark 3 (Real-time implementation): We may note,
that the local filter gains
(i)
k
L
, the error cross-
covariances
(ij)
ksk
(ij)
kk
P,P
+
, and the weights
(i)
k
(i)
sk,
b,a
may
be pre-computed, since they do not depend on the
current observations
.Y
k
But only on the noises
statistics
k
Q
and
(i)
k
R
, and the system matrices
(i)
kkk
H,G,F
, which are part of the system model (1),
(3). Thus, once the observation schedule has been
settled, the real-time implementation of the fusion
predictors FLP and PFF requires only the
computation of the local Kalman estimates
(N)
kk
(1)
kk
x
ˆ
,,x
ˆ
K
and final fusion predictors
FLP
ksk
x
ˆ
+
and
PFF
ksk
x
ˆ
+
.
Remark 4 (Parallel implementation): The local
Kalman estimates
(N)
kk
(1)
kk
x
ˆ
,,x
ˆ
K
are separated for
different sensors. Therefore, they can be
implemented in parallel for various types of
observations
.N1,...,i,y
(i)
k
=
4 EXAMPLES
4.1 Prediction for a Scalar
Multi-sensor System
Consider a scalar system described by
,k,0,1,k,vaxx
Tkk1k
K=+=
+
(23)
,N,1,2,i,wxy
(i)
kk
(i)
k
K=+=
(24)
where
() ()
(
)
.σ,x~x,r0,~w,q0,~v
2
000i
(i)
kk
NNN
This represents the model which takes N sensor
modes. The parameters are subject to
0.9,a
=
,0.2q =
.4N1,σ,0.5x,20k
2
00T
====
The
optimal Kalman predictor, and two fusion predictors
FLP and PFF were used to estimate
.1s,x
sk
≥
+
The
noise statistics were taken as follows:
.5.0r,5.1r.8,1r2.0,r
4321
====
Table 1: Comparison of MSEs at N=3,4.
N=3 Type of Fusion Predictors
k KP FLP PFF
0 1.00000 1.00000 1.00000
1 1.04623 1.04602 1.04623
2 0.96947 0.98315 0.98314
3 0.95727 0.96658 0.96657
4 0.95417 0.96131 0.96131
5 0.95330 0.95962 0.95962
M
M
M
M
10 0.95295 0.95918 0.95918
N=4 Type of Fusion Predictors
k KP FLP PFF
0 1.00000 1.00000 1.00000
1 1.04623 1.04602 1.04623
2 0.95045 0.96037 0.96050
3 0.94361 0.94967 0.94966
4 0.94257 0.94753 0.94753
5 0.94239 0.94718 0.94718
M
M
M
M
10 0.94235 0.94735 0.94735
Table 1 illustrates the mean-square errors (MSEs)
KP
ksk
P
+
,
FLP
ksk
P
+
, and
PFF
ksk
P
+
at the lead
10s =
and
.4,3N
=
Note that the MSEs
FLP
ksk
P
+
and
PFF
ksk
P
+
are very
close and reduced from
3N =
to
.4N =
Moreover,
the differences between the optimal KP and fusion
predictors are negligible, especially for steady-state
regime at
10.k ≥
The numerical simulations were
performed using a computer with the following
specification: Intel® Pentium® 4 CPU 3.0GHz 1G
RAM. The CPU time for evaluation of the estimate
PFF
ksk
x
ˆ
+
is 4.9 times less than for
FLP
ksk
x
ˆ
+
. This is due to
the fact that the PFF’s weights
(i)
k
b
do not depend
on leads
10,...,1s
=
in contrast to the FLP’s weights
(i)
sk,
a
.
4.2 The Damper Harmonic Oscillator
Motion
System model of the harmonic oscillator is
considered in Lewis (1986):
,4t0,v
1
0
x
2
10
x
tt
2
n
t
≤≤
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
−−
=
αω
&
(25)
where
[
]
T
t2,t1,t
xxx =
, and
t1,
x
is position, and
t2,
x
is velocity,
t
v
is zero-mean white Gaussian noise
with intensity q,
(
)()
stqδvvE
st
−
=
,
()
.P,x~x
000
N
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
122
Assume that the observation system contains two
sensors which are observing the position
t1,
x
. Then
we have
,
w
w
x
01
01
y
y
y
(2)
t
(1)
t
t
(2)
t
(1)
t
t
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
(26)
where
)1(
t
w
and
)2(
t
w
are uncorrelated white Gaussian
noises with zero-mean and intensities
1
r
and
2
r
,
respectively.
After discretization of the system and observation
models (25), (26) three predictors were applied: KP,
FLP and PFF. The performance of the fusion
predictors was expressed in the terms of
computation load (CPU time) and loss in estimation
accuracy (MSE) with respect to the optimal KP. The
model parameters, noises statistics, initial conditions,
and lead were taken to
[] []
.10s,1.02.0diagP,0.00.0x
,1r,2r,1q,16.0,64.0
0
T
0
21
2
n
===
=====
αω
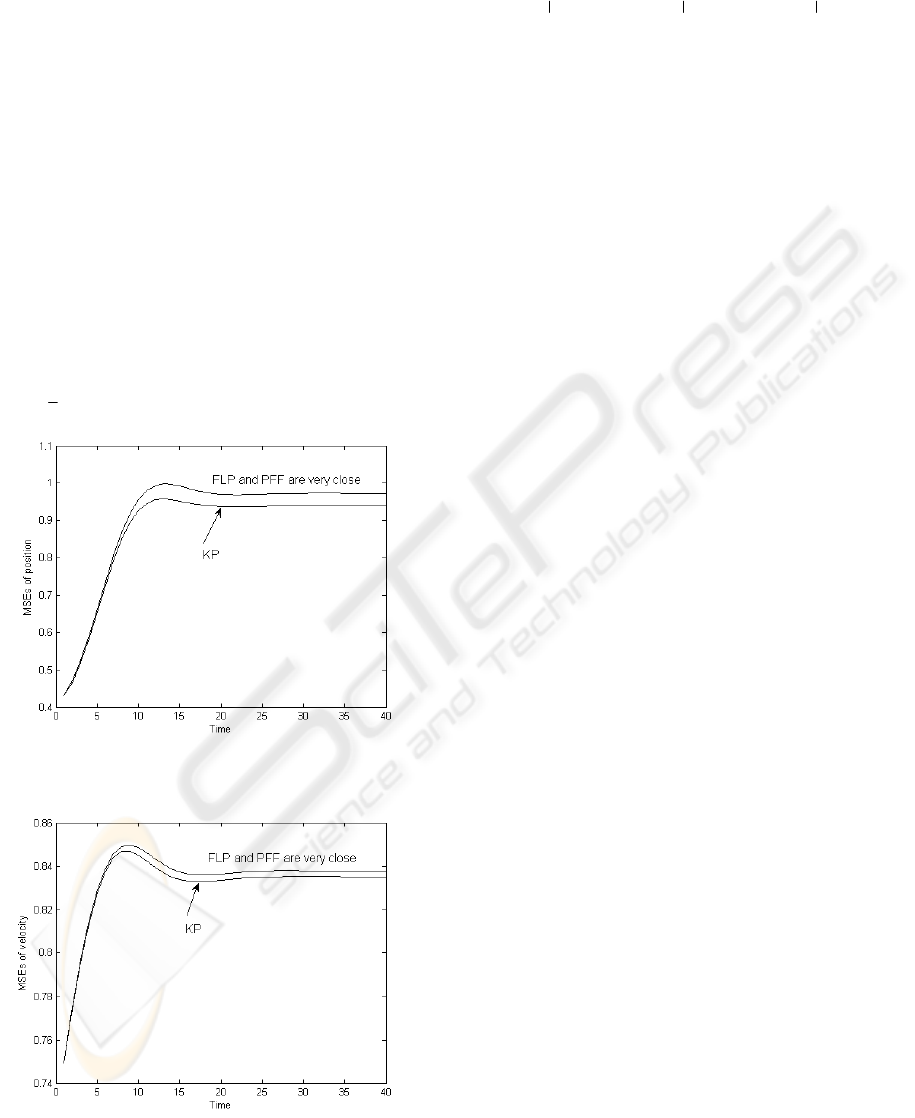
Figure 1: KP, FLP and PFF MSEs for position.
Figure 2: KP, FLP and PFF MSEs for velocity.
In Figs.1 and 2 we show the MSEs for position
(
)
1
x
,
,PP
KP
ksk1,
KP
1
+
= ,PP
FLP
ksk1,
FLP
1
+
= ,PP
PFF
ksk1,
PFF
1
+
=
and
analogously for velocity
()
2
x
PFF
2
FLP
2
KP
2
P,P,P
,
respectively.
The analysis of results in Figs. 1 and 2 shows that
the fusion predictors FLP and PFF have very close
accuracy, i.e.,
.2,1i,PP
PFF
i
FLP
i
=≈
Moreover, the
differences between both fusion MSEs
PFF
i
FLP
i
P,P
,
and optimal one
KP
i
P
are negligible, especially for
steady-state regime. The CPU times for KP, FLP,
and FPP are equaled to
,(s)016.0T,(s)094.0T,0.015(s)T
PFFFLPKP
===
respectively. Thus these combined effects provide
the best balance between the computational
efficiency and desired prediction
accuracy for the
PFF.
5 CONCLUSION
In this paper, we present two fusion predictors (FLP
and PFF) for discrete-time linear systems with
multisensor environment. Both of these predictors
represent the optimal linear combination of an
arbitrary number of local Kalman filters or
predictors. Each local filter (predictor) is fused by
the MMSE criterion. Experimentally the FLP and
PFF algorithms have very close accuracy. In view
of the computational complexity, however, the PFF
more efficient than the FLP. The examples
demonstrate the efficiency and high-accuracy of the
proposed predictors.
REFERENCES
Bar-Shalom, Y., 1990. Multitarget-Multisensor Tracking:
Advanced Applications
, Artech House, Norwood, MA.
Bar-Shalom, Y., Campo, L., 1986. The effect of the
common process noise on the two-sensor used track
covariance, IEEE Trans. Aerospace and Electronic
Systems
, Vol. 22, No. 11, pp. 803-805.
Bar-Shalom, Y., Li, X.R., Kirubarajan, T., 2001.
Estimation with Applications to Tracking and
Navigation
, John Wiley & Sons, New York.
Bar-Shalom, Y., Li, X. Rong, 1995.
Multitarget-
Multisensor Tracking: Principles and Techniques
,
YBS Publishing.
Hall, D. L., 1992. Mathematical Techniques in
Multisensor Data Fusion,
Artech House, London.
FUSION PREDICTORS FOR DISCRETE-TIME LINEAR SYSTEMS WITH MULTISENSOR ENVIRONMENT
123

Lewis, F.L., 1986. Optimal Estimation with an
Introduction to Stochastic Control Theory, John Wiley
& Sons, New York.
Li, X.R., Zhu, Y.M., Wang, J., Han, C.Z., 2004. Optimal
linear estimation fusion – Part I: Unified fusion rules,
IEEE Trans. Inf. Theory
, vol. 49, no. 9, pp. 2192-2208.
Shin, V.I., Lee, Y., Choi, T., 2004. Suboptimal Linear
Filtering and Generalized Millman’s Formula, Proc.
IASTED Inter. Conf. Signal and Image
Process,
Honolulu, Hawaii, USA, pp. 369-374.
Shin, V., Lee, Y., Choi, T.-S., 2006. Generalized
Millman's formula and its applications for estimation
problems,
Signal Processing, vol.86, No.2, pp. 257-
266.
Zhou, J., Zhu, Y., You, Z., Song, E., 2006. An efficient
algorithm for optimal linear estimation fusion in
distributed multisensor systems,
IEEE Trans. Syst.,
Man, Cybern.
, vol.36, no.5, pp. 1000-1009.
APPENDIX
Proof of Theorem and Corollary:
(a) Equations (12) and expression (13)
immediately follow as a result of application of the
general FF (Shin et al. 2006 and Zhou et al. 2006) to
the optimization problem (11).
(b) Equation for the local error takes the form
.vGx
~
Fx
ˆ
-xx
~
1sk1sk
(i)
k1-sk
1sk
(i)
ksk
sk
(i)
ksk
−+−+
+
−+
+
+
+
+==
Then equation for the cross-covariance (15)
associated with the
(i)
ksk
x
~
+
and
(j)
ksk
x
~
+
follows from the
standard propagation equation for
(
)
.x
~
x
~
EP
T
(j)
ksk
(i)
ksk
(ij)
ksk +++
=
Equation (16) was given in Shin et al. (2006).
(c) Using (10) the fusion error covariance can be
rewritten as
(
)
()
.aPax
~
ax
~
aE
x
ˆ
axx
ˆ
axE
)x
ˆ
-(x)x
ˆ
-(xEP
N
1ji,
(j)
sk,
(ij)
ksk
(i)
sk,
N
1j
T
(j)
ksk
(j)
sk,
N
1i
(i)
ksk
(i)
sk,
T
N
1j
(j)
ksk
(j)
sk,sk
N
1i
(i)
ksk
(i)
sk,sk
TFLP
ksk
sk
FLP
ksk
sk
FLP
ksk
T
∑∑∑
∑∑
=
+
=
+
=
+
=
+
+
=
+
+
+
+
+
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
−⋅
⎥
⎦
⎤
⎢
⎣
⎡
−=
⋅=
This completes
the proof of Theorem.
If the local predictors
(i)
ksk
x
ˆ
+
are unbiased, i.e.,
(
)
(
)
sk
(i)
ksk
xEx
ˆ
E
+
+
=
, then we have
(
)
(
)
()()
.xExEax
ˆ
Eax
ˆ
E
N
1i
sksk
N
1i
(i)
sk,
(i)
ksk
(i)
sk,
FLP
ksk
∑∑
=
++
=
++
=
⎥
⎦
⎤
⎢
⎣
⎡
==
Corollary is proved.
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
124
