
K2: A STREAM CIPHER ALGORITHM
USING DYNAMIC FEEDBACK CONTROL
Shinsaku Kiyomoto, Toshiaki Tanaka
KDDI R & D Laboratories Inc., 2-1-15 Ohara Fujimino-shi Saitama 356-8502, Japan
Kouichi Sakurai
Kyushu University, 744 Motooka Nishi-ku Fukuoka 819-0395, Japan
Keywords:
Stream Cipher, Dynamic Feedback Control, Irregular Clocking, Pseudorandom Generator.
Abstract:
A variety of different clock-controlled stream ciphers and attacks on them have been described in a number of
papers. However, few word-oriented algorithms with an irregular clocking mechanism have been proposed.
This paper proposes a new design of irregular clocking for word-oriented stream ciphers that is dynamic
feedback control and show analysis results of its security and performance. The stream cipher K2 v2.0 is
a secure and high-performance stream cipher using the dynamic feedback control, which is applicable for
several applications. We believe that the dynamic feedback control mechanism is potentially effective against
several different types of attacks, not only existing attacks but also novel attacks.
1 INTRODUCTION
Stream ciphers are used extensively to provide a re-
liable, efficient method for secure communications.
A basic stream cipher uses several independent linear
feedback shift registers (LFSRs) together with non-
linear functions in order to produce a keystream. The
keystream is then XORed with plaintext to produce a
ciphertext. Some stream ciphers use a general non-
linear function to clock one or more LFSR(s) irregu-
larly. Various clock-controlled stream ciphers and at-
tacks on them have been proposed. Clock-controlled
stream ciphers are classified into two main types of
stream ciphers: the A5 family and the LILI family.
A5 is a well-known stream cipher designed to ensure
the confidentiality of mobile communications. LILI-
like stream ciphers, such as LILI-128 (Simpson et al.,
2000), have two different LFSRs for providing bits for
clocking and keystream bits. One LFSR clocks reg-
ularly, providing input for a clock controller, and an-
other LFSR clocks irregularly, providing keystream.
Recently, word-oriented stream ciphers have been
developed in order to improve the performance of
software implementations. In the NESSIE project,
many word-oriented stream ciphers were proposed,
such as SNOW(Ekdahl and Johansson, 2000) and
SOBER(Rose and Hawkes, 1999), and demonstrated
good performance in software. However, few word-
oriented algorithms with an irregular clocking mech-
anism have been proposed because of the inefficiency
of the clock control mechanism for software imple-
mentation. LFSR-based stream ciphers have been
broken using a linear recurrence of the LFSR. Thus,
an irregular clocking mechanism for word-oriented
LFSRs will achieve an improvement of their security.
This paper proposes a new word-oriented stream
cipher using dynamic feedback control as irregular
clocking. The proposed stream cipher has a dy-
namic feedback control mechanism for the byte-level
feedback function of FSRs and realizes fast encryp-
tion/decryption for software implementation. We
present a stream cipher algorithm and show the re-
sults of an analysis of security and performance, and
show that the cipher is secure and it offers high-
performance encryption and decryption.
2 DYNAMIC FEEDBACK
CONTROL
The clock control mechanism of a stream cipher gen-
erally either controls LFSR clocking or shrinks or
thins output. A clock control that shrinks or thins out-
204
Kiyomoto S., Tanaka T. and Sakurai K. (2007).
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL.
In Proceedings of the Second International Conference on Security and Cryptography, pages 204-213
DOI: 10.5220/0002122302040213
Copyright
c
SciTePress

put reduces the performance of the stream cipher be-
cause some output bits are discarded. If one applies
shrinking to a word-oriented stream cipher, the per-
formance is markedly reduced. The bit-oriented clock
control mechanism for updating an LFSR is also in-
efficient when the mechanism controls the LFSR for
each register. On the other hand, a dynamic feedback
control for an LFSR is an effective method for im-
proving the security of stream ciphers. The stream
cipher MICKEY(Babbage and Dodd, 2005) has a
dynamic feedback control mechanism for a bit-wise
LFSR. POMARANCH(Jansen et al., 2005) uses a
cascade jump controlled sequence generator to mod-
ify the feedback function.
We propose a stream cipher design (called
KARAKORUM type) that operates on words and has
an efficient dynamic feedback control as irregular
clocking. The basic idea of the design is to modify
the mixing operation during the state update. Feed-
back polynomials for word-oriented LFSR are de-
scribed with coefficients; multiplying an input word
by a coefficient means mixing the words. A typical
example is a LFSR of SNOW 2.0(Ekdahl and Johans-
son, 2003). Generally, the coefficients are selected
such that the feedback polynomial is a primitive poly-
nomial. We apply irregular clocking for this mixing
operation, and the modification causes only a mini-
mal decrease in the encryption/decryption speed. In
other words, at least one FSR is irregularly clocked
to dynamically modify the feedback function to the
dynamic feedback controller that receives the out-
puts of the other FSR(s). For example, the feedback
function is defined as s
t+a
= α
{0,1}
0
s
t+b
⊕α
{0,1}
1
s
t+c
⊕
α
{0,1}
2
s
t+d
, where {0,1}s are selected by the dynamic
feedback controller. The FSR controlled by the dy-
namic feedback controller is named dynamic feed-
back shift register (DFSR).
The dynamic feedback control mechanism im-
proves the security of a stream cipher because it
changes the deterministic linear recurrence of some
registers into a probabilistic recurrence. This prop-
erty effectively protects against several attacks. An
attacker has to obtain the linear recurrence of the
keystream derived from the linear recurrence of some
registers. By an irregular modification, the linear re-
currence exists with a low probability. An attacker has
to guess some inputs to the non-linear function for
an attack; however, an irregular modification makes
it impossible: the attacker has to guess the inputs to
the dynamic feedback controller first. Thus, irregular
modification of the feedback function improves the
security of the stream cipher.
We think that a dynamic feedback control mech-
anism is potentially effective against several attacks,
not only existing attacks but also a novel attack.
3 STREAM CIPHER K2 V2.0
In this section, we describe the stream cipher algo-
rithm K2 v2.0
1
that has a dynamic feedback control
mechanism.
3.1 Linear Feedback Shift Registers
The K2 v2.0 stream cipher consists of two feedback
shift registers (FSRs), FSR-A and FSR-B, a non-linear
function with four internal registers R1, R2, L1, and
L2, and a dynamic feedback controller as shown in
Fig. 1. FSR-B is a dynamic feedback shift register.
The size of each register is 32 bits. FSR-A has five
registers, and FSR-B has eleven registers. Let β be
the roots of the primitive polynomial;
x
8
+ x
7
+ x
6
+ x+ 1 ∈ GF(2)[x]
A byte string y denotes (y
7
,y
6
,...,y
1
,y
0
), where y
7
is the most significant bit and y
0
is the least significant
bit. y is represented by
y = y
7
β
7
+ y
6
β
6
+ ... + y
1
β+ y
0
In the same way, let γ, δ, ζ be the roots of the
primitive polynomials,
x
8
+ x
5
+ x
3
+ x
2
+ 1 ∈ GF(2)[x]
x
8
+ x
6
+ x
3
+ x
2
+ 1 ∈ GF(2)[x]
x
8
+ x
6
+ x
5
+ x
2
+ 1 ∈ GF(2)[x]
respectively.
Let α
0
be the root of the irreducible polynomial of
degree four
x
4
+ β
24
x
3
+ β
3
x
2
+ β
12
x+ β
71
∈ GF(2
8
)[x]
A 32-bit string Y denotes (Y
3
,Y
2
,Y
1
,Y
0
), where Y
i
is a byte string and Y
3
is the most significant byte. Y
is represented by
Y = Y
3
α
3
0
+Y
2
α
2
0
+Y
1
α
0
+Y
0
Let α
1
, α
2
, α
3
be the roots of the irreducible poly-
nomials of degree four
x
4
+ γ
230
x
3
+ γ
156
x
2
+ γ
93
x+ γ
29
∈ GF(2
8
)[x]
x
4
+ δ
34
x
3
+ δ
16
x
2
+ δ
199
x+ δ
248
∈ GF(2
8
)[x]
1
A previous version of the algorithm is shown in the
SASC 2007 workshop record(Kiyomoto et al., 2007).
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL
205
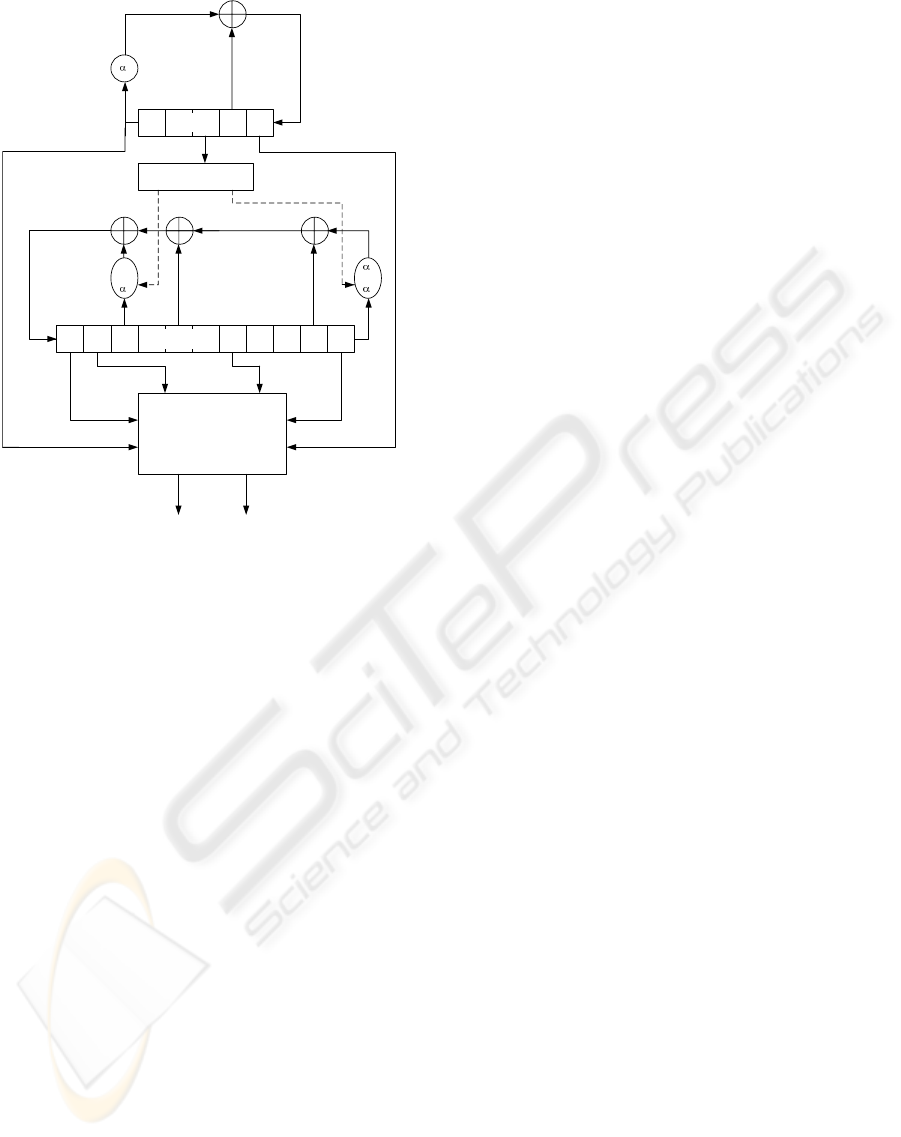
Dynamic Feedback
Controller
B
t
FSR-B
0
A
t
FSR-A
Non-Linear Function
Keystream (64bits)
1
or
2
B
t+10
A
t+4
1
or
3
z
H
t
z
L
t
Figure 1: K2 v2.0 Stream Cipher.
x
4
+ ζ
157
x
3
+ ζ
253
x
2
+ ζ
56
x+ ζ
16
∈ GF(2
8
)[x]
respectively.
The feedback polynomials f
A
(x), and f
B
(x) of
FSR-A and FSR-B, respectively, are as follows;
f
A
(x) = α
0
x
5
+ x
2
+ 1
f
B
(x) = (α
cl1
t
1
+α
1−cl1
t
2
−1)x
11
+x
10
+x
5
+α
cl2
t
3
x
3
+1
Let cl1 and cl2 be the sequences describing the
output of the dynamic feedback controller. The out-
puts at time t are defined in terms of some bits of FSR-
A. Let A
x
denote the output of FSR-A at time x, and
A
x
[y] = {0, 1} denote the yth bit of A
x
, where A
x
[31] is
the most significant bit of A
x
. Then cl1 and cl2 (called
clock control bits) are described as follows;
cl1
t
= A
t+2
[30], cl2
t
= A
t+2
[31]
Both cl1
t
and cl2
t
are binary variables; more pre-
cisely, cl1
t
= {0,1}, and cl2
t
= {0,1}. Stop-and-go
clocking is effective in terms of computational cost,
because no computation is required in the case of
0. However, the feedback function has no transfor-
mation for feedback registers with a probability 1/4
where all clockings are stop-and-go clockings. Thus,
we use two types of clocking for the feedback func-
tion. FSR-B is defined by a primitive polynomial,
where cl2
t
= 0.
3.2 Nonlinear Function
The non-linear function of K2 v2.0 is fed the values
of two registers of FSR-A and four registers of FSR-
B and that of internal registers R1, R2, L1, L2, and
outputs 64 bits of the keystream every cycle. Fig. 2
shows the non-linear function of K2 v2.0. The non-
linear function includes four substitution steps that are
indicated by Sub.
The Sub step divides the 32-bit input string into
four 1-byte strings and applies a non-linear permuta-
tion to each byte using an 8-to-8 bit substitution, and
then applies a 32-to-32 bit linear permutation. The
8-to-8 bit substitution is the same as s-boxes of AES
(Daemen and Rijmen, 1998), and the permutation is
the same as AES Mix Column operation. The 8-to-
8 bit substitution consists of two functions: g and
f. The g calculates the multiplicative inverse mod-
ulo the irreducible polynomial m(x) = x
8
+ x
4
+ x
3
+
x+ 1 without 0x00, and 0x00 is transformed to itself
(0x00). f is an affine transformation defined by;
b
7
b
6
b
5
b
4
b
3
b
2
b
1
b
0
=
11111000
01111100
00111110
00011111
10001111
11000111
11100011
11110001
×
a
7
a
6
a
5
a
4
a
3
a
2
a
1
a
0
⊕
0
1
1
0
0
0
1
1
where a = (a
7
,...,a
0
) is the input and b = (b
7
,...,b
0
)
is an output, and a
0
and b
0
are the least significant bit
(LSB).
Let C be (c
3
,c
2
,c
1
,c
0
) and output D be
(d
3
,d
2
,d
1
,d
0
), where c
i
, d
i
are 8-bit values. The lin-
ear permutation D = p(C) is described as follows;
d
0
d
1
d
2
d
3
=
02 03 01 01
01 02 03 01
01 01 02 03
03 01 01 02
c
0
c
1
c
2
c
3
in GF(2
8
) of the irreducible polynomial m(x) = x
8
+
x
4
+ x
3
+ x+ 1.
3.3 Keystream Output
Let keystream at time t be Z
t
= (z
H
t
,z
L
t
) (each z
x
t
is a
32-bit value, and z
H
t
is a higher string). The keystream
z
H
t
, z
L
t
is calculated as follows:
z
L
t
= B
t
⊞ R2
t
⊕ R1
t
⊕ A
t+4
z
H
t
= B
t+10
⊞ L2
t
⊕ L1
t
⊕ A
t
where A
x
and B
x
denote outputs of FSR-A and FSR-B
at time x, and R1
x
, R2
x
, L1
x
, and L2
x
denote the inter-
nal registers at time x. The symbol ⊕ denotes bitwise
SECRYPT 2007 - International Conference on Security and Cryptography
206
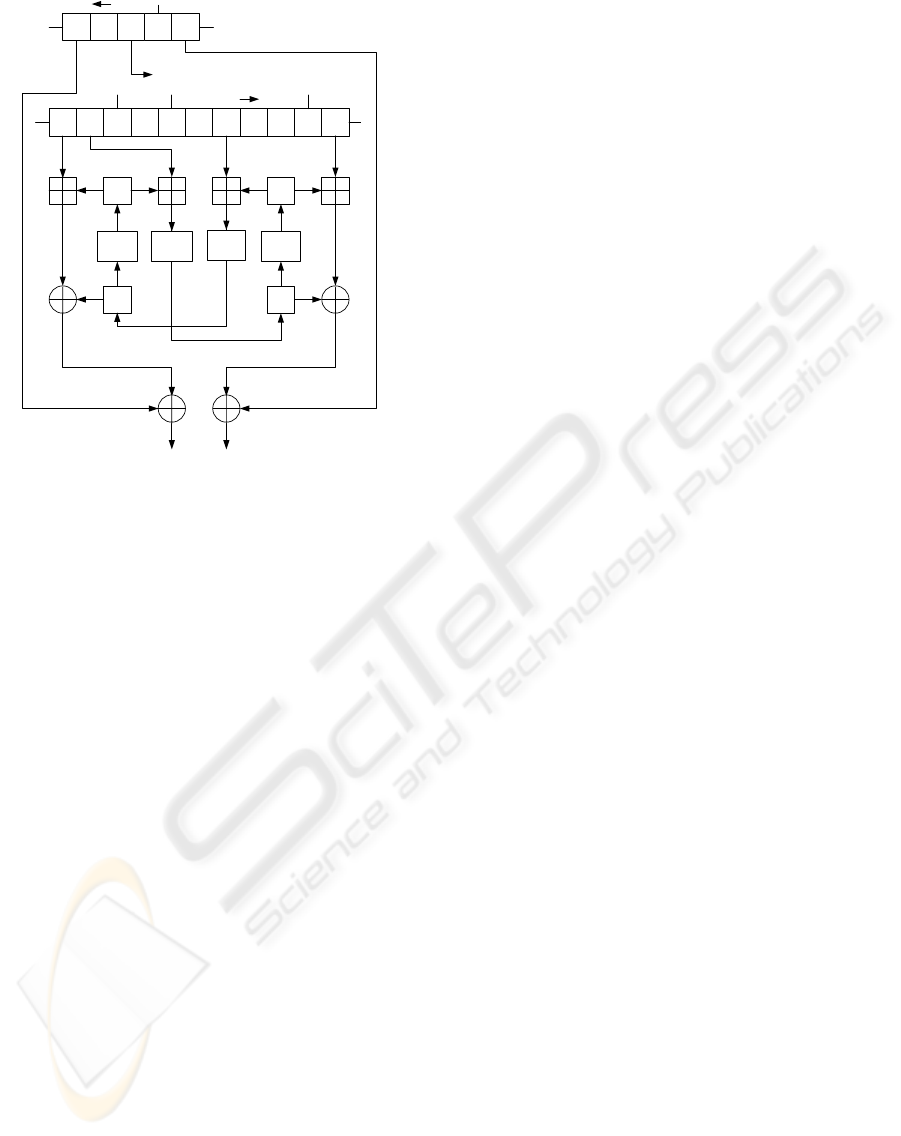
04910
R2
20
FSR-B
FSR-A
Keystream (64bits)
Dynamic Feedback Controller
L2
4
Sub
L1
Sub
R1
Sub
Sub
Figure 2: Non-Linear Function of K2 v2.0.
exclusive-or operation and the symbol ⊞ denotes and
32-bit addition. Finally, the internal registers are up-
dated as follows;
R1
t+1
= Sub(L2
t
⊞ B
t+9
), R2
t+1
= Sub(R1
t
)
L1
t+1
= Sub(R2
t
⊞ B
t+4
), L2
t+1
= Sub(L1
t
)
where Sub(X) is an output of the Sub step for X.
The set of {B
t
,B
t+3
,B
t+8
,B
t+10
} is a Full Positive
Difference Set (FPDS)(Golic, 1996).
3.4 Initialization Process
The initialization process of K2 v2.0 consists of
two steps, a key loading step and an internal state
initialization step. First, an initial internal state is
generated from a 128-bit initial key, a 192-bit initial
key, or a 256-bit initial key and a 128-bit initial
vector (IV) by using the key scheduling algorithm.
The key scheduling algorithm is similar to the round
key generation function of AES and the algorithm
extends the 128-bit initial key, the 192-bit initial
key or the 256-bit initial key to 384 bits. The key
scheduling algorithm for a 128-bit key is described as
K
i
=
IK
i
(0 ≤ i ≤ 3)
K
i−4
⊕ Sub((K
i−1
≪ 8) ⊕ (K
i−1
≫ 24))
⊕Rcon[i/4− 1] (i = 4n)
K
i−4
⊕ K
i−1
(i 6= 4n)
where IK = (IK
0
,IK
1
,IK
2
,IK
3
) is the initial key, i is
a positive integer 0 ≤ i ≤ 11, and n is a positive in-
teger. The function Sub(X) in the key scheduling al-
gorithm is the same as that in the non-linear function.
This function is different from the round key gener-
ation function of AES, and the other part of the key
scheduling algorithm is same as the AES round key
generation. Rcon[i] denotes (x
i
mod x
8
+ x
4
+ x
3
+
x + 1, 0x00,0x00,0x00) and x is 0x02. The internal
state is initialized with K
i
and IV = (IV
0
,IV
1
,IV
2
,IV
3
)
as follows:
A
m
= K
4−m
(m = 0,..., 4),B
0
= K
10
,B
1
= K
11
,
B
2
= IV
0
,B
3
= IV
1
,B
4
= K
8
,B
5
= K
9
,B
6
= IV
2
,
B
7
= IV
3
,B
8
= K
7
,B
9
= K
5
,B
10
= K
6
The internal registers, R1, R2, L1, and L2 are set to
0x00. After the above processes, the cipher clocks 24
times (j = 1, ..., 24), updating the internal states. The
internal states A
j+4
B
j+10
are also updated as follows:
A
j+4
=α
0
A
j−1
⊕ A
j+2
⊕ z
L
j−1
B
j+10
=(α
cl1
j−1
1
+ α
1−cl1
j−1
2
− 1)B
j−1
⊕ B
j
⊕ B
j+5
⊕ α
cl2
j−1
3
B
j+7
⊕ z
H
j−1
The recommended maximum number of cycles
for K2 v2.0 without re-initializing is 2
58
cycles (2
64
keystream bits).
4 ANALYSIS OF K2 V2.0
4.1 Analysis of Periods
The cipher has two FSRs. FSR-A is defined by a
primitive polynomial. Thus, the sequence of 32-bit
outputs generated by FSR-A has a maximum period
of 2
160
− 1.
Now, we re-define the updating function f
B
for
FSR-B in terms of a 352 × 352 matrix M
f
B
over
GF(2). The updating function at time t is given by
one of the four possibilities for the matrix. The period
of outputs of FSR-B is l, where l is a minimum value
satisfying (M
f
B
)
l
= I. The matrix is described as
follows:
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL
207

M
f
B
=
0 I 0 0 0 0 0 0 0 0 0
0 0 I 0 0 0 0 0 0 0 0
0 0 0 I 0 0 0 0 0 0 0
0 0 0 0 I 0 0 0 0 0 0
0 0 0 0 0 I 0 0 0 0 0
0 0 0 0 0 0 I 0 0 0 0
0 0 0 0 0 0 0 I 0 0 0
0 0 0 0 0 0 0 0 I 0 0
0 0 0 0 0 0 0 0 0 I 0
0 0 0 0 0 0 0 0 0 0 I
M
1
0 I 0 0 I 0 0 M
2
0 0
where M
1
= M
α
2
,M
α
1
(cl1
t
= 0, 1), M
2
= I,M
α
3
(cl2
t
= 0,1). M
α
1
, M
α
2
, and M
α
3
are shown in Ap-
pendix A.
We calculated the periods of FSR-B for the four
possible representations as follows:
• (cl1
t
,cl2
t
) = (0,0)
The matrix M
f
B
has the maximum order 2
352
− 1,
and output sequences of the FSR-B have a maxi-
mum period 2
352
− 1. The FSR-B is a linear feed-
back shift register where the feedback polynomial
f
B
is a primitive polynomial over GF(2).
• (cl1
t
,cl2
t
) = (1,0)
The matrix M
f
B
has the maximum order 2
352
− 1,
and output sequences of the FSR-B also have the
maximum period 2
352
− 1.
• (cl1
t
,cl2
t
) = (0,1)
The matrix M
f
B
has an order of approximately
2
332
, and output sequences of the FSR-B have a
period of approximately 2
332
.
• (cl1
t
,cl2
t
) = (1,1)
The matrix M
f
B
has an order of approximately
2
318
, and output sequences of the FSR-B have a
period of approximately 2
318
.
From the above results of analysis, we think that
K2 v2.0 can produce a keystream of a sufficient length
period more than the number of cycles without re-
initialization. In an experimental analysis using some
sequences of the keystream produced by the cipher,
we did not find any short periods.
4.2 Analysis of Statistical Tests
The statistical properties of the cipher also depend on
the properties of the output sequences of FSR-A and
FSR-B; thus, we expect the keystream of the cipher
to have good statistical properties. We evaluated the
statistical properties for the keystream of the cipher
and output sequences of FSR-A and FSR-B by the
NIST Test Suite
2
and confirmed that these properties
2
Random Number Generation and Testing, NIST Test
Suite, Available from http://csrc.nist.gov/rng/.
were good.
4.3 Security Analysis
We discuss security of the cipher against existing
attacks.
Time-Memory Trade-Offs. We chose the size
of the secret key and IV taking into consideration
the discussion of general time-memory trade-offs by
Hong and Sarker (Hong and Sarkar, 2005). This at-
tack generally requires O(2
3(k+v)
4
) pre-computation,
O(2
k+v
2
) memory, and O(2
k+v
2
) available data, en-
abling an online attack with time complexity of
O(2
k+v
2
), where the lengths of the secret key and IV
are k and v, respectively.
The IV, the secret key, and the internal state are
sufficiently large. Thus, we think the cipher is not
vulnerable to time-memory trade-off attacks.
Correlation Attacks. The feasibility of cor-
relation attacks depends on the number of inputs
to the non-linear function and on the tap positions
for the function. The use of a full positive differ-
ence set for the tap positions and the non-linear
function has sufficient non-linearity for preventing
the attacks. We evaluate the security using an
asymptotic analysis proposed by Chepyzhov and
Smeets (Chepyzhov et al., 2001). The required
length N of the keystream for an correlation attack
is N ≈ 1/4 · (2k · h! · ln2)
1/h
· ε
−2
· 2
l−k
h
, where l, k,
and h denote a target FSR length, and algorithm
parameters, and the correlation probability of the
target stream cipher is 1/2 + ε. The computational-
time complexity of this pre-computation phase in
the attack is approximately N
⌈(h−1)/2⌉
and N
⌊(h−1)/2⌋
is required. Furthermore, the decoding algorithm
stores (N
h
· 2
k−l
)/h! parity checks and its com-
putational complexity is 2
k
times the number of
parity checks. When attacking the regular clocked
FSR-B in K2, the lowest correlation probability
for the attack is approximately 1/2 + 2
−13
, where
h = 9, k = 26, and computational complexity and the
required memory are roughly O(2
256
). However, no
correlation between the input and output sequences
of the non-linear function with a probability larger
than 1/2+ 2
−13
is found. Furthermore, the irregular
clocking improves security against correlation attacks
because the linear relations of bits in FSR-B are more
complicated using the irregular clock.
Security of the Initialization Process. For
any key unique pair of a initial key and a IV, the
SECRYPT 2007 - International Conference on Security and Cryptography
208

key loading step generates an internal state of the
cipher. The initial key is expanded using the AES key
scheduling algorithm, and the IV and expanded keys
are thoroughly mixed by the 24 cycles comprising
the initialization process. After 13 cycles of the
run-up, all values of an internal state of the cipher
includes all IV
i
s. All registers in the internal state
will depend on both the initial key and IV after
13 cycles. Furthermore, the initialization process
additionally runs 11 cycles and the IV
i
s and an initial
key are well mixed into the internal state. Even an
initial difference of any single register for the IV is
propagated to all registers in the internal state after 12
steps. Thus, we think that the cipher is not vulnerable
to the chosen/related IV attacks. Another attack to
the initialization process is a distinguishing attack
to use a collision of the first keystream by chosen
pairs of an initial key and a IV. However, we did
not find the collision that is occurred with a feasible
probability, because any registers are well mixed.
Guess-and-Determine Attacks.
First, we discuss the general evaluation of the
computational complexity of guess-and-determine at-
tacks. The keystream of n bits is calculated from m
bits of the output of an internal state of l bits, which
consists of FSRs and the internal memory of a non-
linear function. In the initial step, an adversary can
determine n bits of the internal state from n bits of
the keystream, which allow guessing of m− n bits of
the internal state. In the next step, some values of the
internal state will have already been guessed or deter-
mined in the previous step. In this manner, the ad-
versary guesses other values of the internal state. The
adversary iteratively performs guesses and determines
steps until all values of the internal state have either
been guessed or determined. Now, we assume that m
bits of the output are uniformly selected from internal
state by an ideal rule. After j steps, the values that
the adversary has had to guess can be approximated
as
1− ⌈
v
j
l
⌉
(m− n), where v
j
is the number of bits
that have already been guessed or determined in step
j. Let y(x) denote the number of already-guessed or
determined bits at the xth step of the GD attack. and
set y(0) = 0. Now, we assume that n bits of the in-
ternal state can be determined in each step. y(x) is
caluclated as;
y(x) =
n
2
− m· n+ l · m
m− n
1− e
−
m−n
l
x
We obtain η the number of steps needed for the
GD attack from y(η) = l. Thus, the total number η
of guessed and determined steps can be approximated
by η ≈
l
m−n
· ln
m
n
.
The computational cost C is C ≈ c· 2
l−nη
, where c
is a constant value. For K2, l, m, and n are 640, 256,
and 64 respectively. Thus, the computational com-
plexity is approximately O(2
344
). As a result of the
general evaluation of GD attacks, K2 is expected to
be secure against GD attacks.
A simple guess-and-determine attack is where the
attacker guesses all values of FSR-A and all inter-
nal memory sets and determines all values of FSR-
B. However, this attack is impossible because the
computational complexity of the attack is at least
O(2
288
). Now, we consider a guess-and-determine at-
tack against a simplified K2 that is performed with-
out multiplying α
i
(i = 0,1,2, 3) and additions are re-
placed by exclusive-or operations. First, we consider
an attack designed to remove A
t+4
from the equation
of the keystream and to attack with the focus on FSR-
B as follows:
z
L
t
⊕ z
H
t+4
= (B
t
⊞ Sub(R1
t−1
)) ⊕ R1
t
⊕ (B
t+14
⊞ Sub(L1
t−1
)) ⊕ L1
t+4
If an attacker guesses five elements of the above
equation, then the attacker can determine the other el-
ement, such as B
t+14
, and the attacker can also de-
termine A
t+4
. To determine all values of FSRs, the
attacker has to guess at least 10 elements; thus, this
attack is impossible. Next, we consider the other at-
tack where the relationship of four internal registers
R1, R2, L1, L2 is used. The relationship of the mem-
ory is described as follows;
R2
t+1
= Sub(R1
t
), L1
t+2
= Sub(R2
t+1
⊞ B
t+5
)
L2
t+3
= Sub(L1
t+2
), R1
t+4
= Sub(L2
t+3
⊞ B
t+12
)
That is, if an attacker guesses R1
t
, B
t+5
, B
t+12
,
then the attacker determines R2
t+1
, L1
t+2
, L2
t+3
,
R1
t+4
using the above equations. Now, consider a
more simplified algorithm without FSR-A, which
is that the attacker obtains the values of z
H
t
⊕ A
t
and z
L
t
⊕ A
t+4
in each cycle t. In this situation,
if the attacker guesses six elements R1
t+1
, R1
t+2
,
L1
t
, L1
t+1
, B
t+6
, and B
t+7
, then the attacker can
determine all values of FSR-B. The complexity of the
second attack is O(2
192
). However, more than two
values of FSR-A have to be guessed for obtaining all
values of the internal state. Furthermore, the attacker
needs to guess the clock control bits for the full
version algorithm. Thus, we think the full version of
the algorithm is secure against guess-and-determine
attacks.
Distinguishing Attacks. In distinguishing at-
tacks, a probabilistic linear relation of keystream
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL
209
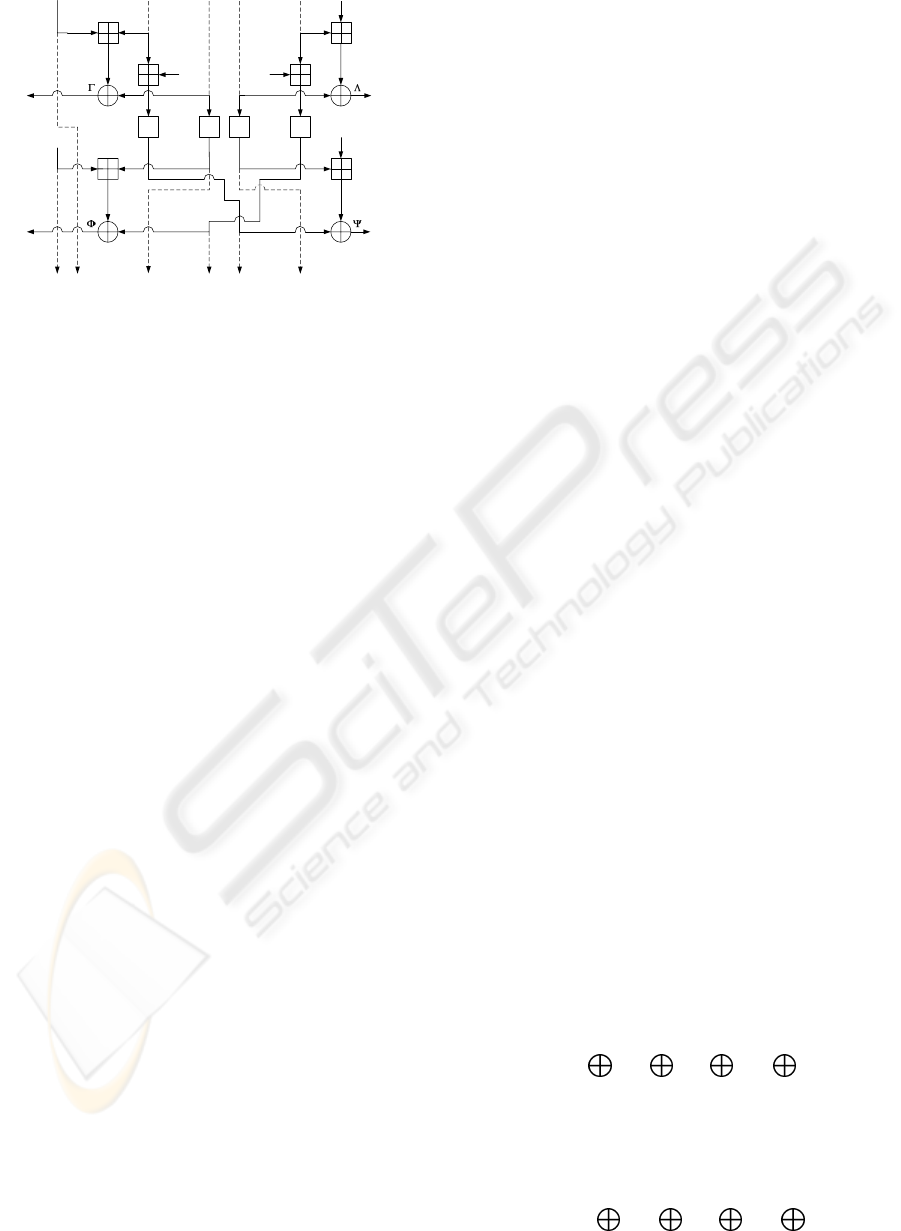
Sub
B
t+9
Sub
B
t+10
B
t+11
Sub Sub
B
t+5
B
t
B
t+1
L2
t
L1
t
R1
t
R2
t
Z
L
t
+A
t
Z
L
t+1
+A
t+1
Z
R
t
+A
t+4
Z
R
t+1
+A
t+5
Figure 3: Linear Masking of K2 for Two-Round Outputs.
bits is needed as a distinguisher. K. Nyberg and J.
Wallen presented a distinguishing attack on SNOW
2.0(Nyberg and Wallen, 2006) where the computa-
tional complexity of their attack was O(2
174
). We try
to construct a linear recurrence from output keystream
bits with fixed clock control bits cl1
t
= cl2
t
= 0 for
each cycle. A two-round linear masking of K2 is
shown in Fig. 3. Four substitutions are affected by the
linearization; the number of involved substitutions is
twice the number of attacks on SNOW 2.0. Thus, we
expect that K2 is more secure than SNOW 2.0 against
distinguishing attacks.
Now, we construct a linear distinguisher using
four masks, Γ, Λ, Φ, and Ψ as follows;
Γα
2
α
0
· Σ
z
H
(t) ⊕ Γα
2
· Σ
z
H
(t + 3,t + 5)
⊕ Γα
0
· Σ
z
H
(t + 1,t + 6,t + 8,t + 11)
⊕ Γ· Σ
z
H
(t + 4,t + 6,t + 9,t + 13,t + 14,t + 16)
⊕ Λα
2
α
0
· Σ
z
L
(t) ⊕ Λα
2
· Σ
z
L
(t + 3,t + 5)
⊕ Λα
0
· Σ
z
L
(t + 1,t + 6,t + 8,t + 11)
⊕ Λ· Σ
z
L
(t + 4,t + 6,t + 9,t + 13,t + 14,t + 16)
⊕ Φα
2
α
0
· Σ
z
H
(t + 1) ⊕ Φα
2
· Σ
z
H
(t + 4,t + 6)
⊕ Φα
0
· Σ
z
H
(t + 2,t + 7,t + 9,t + 12)
⊕ Φ· Σ
z
H
(t + 5,t + 7,t + 10,t + 14,t + 15,t + 17)
⊕ Ψα
2
α
0
· Σ
z
L
(t + 1) ⊕ Ψα
2
· Σ
z
L
(t + 4,t + 6)
⊕ Ψα
0
· Σ
z
L
(t + 2,t + 7,t + 9,t + 12)
⊕ Ψ· Σ
z
L
(t + 5,t + 7,t + 10,t + 14,t + 15,t + 17) = 0
If the bias for a combination of linear masks
has a high probability, an attacker constructs a
distinguisher from the equation. However, we have
not found a combination of linear masks with a bias
value higher than 2
−128
. Furthermore, to obtain
the equation, all clock control bits for 15 times the
feedback operations of FSR-B are cl1
t
= cl2
t
= 0;
the probability of this condition of clock control bits
is about 2
−30
. That is, the computational complexity
of a distinguishing attack against the cipher increase
2
60
times by using the dynamic feedback control
mechanism. Additionally, the cipher is assumed to be
re-initialized after 2
58
cycles. Thus, we conclude that
distinguishing attacks against K2 is impossible.
Algebraic Attacks. The non-linear function has
ideal algebraic properties; the non-linear function
consists of AES S-boxes and an effective permutation
function. Furthermore, the dynamic feedback control
increases the cost of solving the system of internal
values. Courtois presented an evaluation method for
the complexity of general algebraic attacks (Courtois,
2005). A general evaluation suggests that K2 is secure
against algebraic attacks; the computational complex-
ity of the attack is roughly O(2
646
).
We investigated the possibility of algebraic at-
tacks, when we assumed that FSR-B has regular
clocking and the addition modulo 2
32
operation is re-
placed by the XOR operation. An algebraic attack
against SNOW 2.0 was proposed by O. Billet and H.
Gilbert(Billet and Gilbert, 2005). We tried to apply
the attack to K2. This attack is effective for stream
cipher algorithms that have a non-linear function with
internal memory. In this attack, the attacker has to
have internal registers at time t, which is defined as
linear equations that consist of initial values of in-
ternal state variables, and constructs relationships be-
tween the input values of a non-linear substitution and
the corresponding output values, which are low de-
gree algebraic expressions.
First, we obtain the following equation from the
assumption:
R2
t
= R1
t
⊕A
t+4
⊕B
t
⊕z
L
t
, L1
t−1
= Sub(R2
t−2
⊕B
t+2
)
R1
t
= Sub(L1
t−1
⊕ A
t−1
⊕ B
t+8
⊕ B
t+9
⊕ z
H
t−1
)
If we remove substitutions from the above equa-
tions, we obtain the linear recurrence R2
t
= R2
t−2
⊕
A
t−1
⊕ A
t+4
⊕ B
t
⊕ B
t+2
⊕ B
t+8
⊕ B
t+9
⊕ z
H
t−1
⊕ z
L
t
.
We can define a linear equation of registers of
FSR-A and FSR-B, for any clock t, which only in-
volves keystream, registers at t = 0, and R2
0
from the
equation for R2
t
;
R2
t
= R2
0
t
i=0
ε
i
t
z
H
i
t
j=0
ε
j
t
z
L
j
4
k=0
ε
k
t
A
k
10
l=0
ε
l
t
B
l
where ε
i
t
, ε
j
t
, ε
k
t
, ε
l
t
are known binary coefficients.
We also obtain;
R1
t−1
= R1
0
t
i=0
ε
i
t
z
H
i
t
j=0
ε
j
t
z
L
j
4
k=0
ε
k
t
A
k
10
l=0
ε
l
t
B
l
SECRYPT 2007 - International Conference on Security and Cryptography
210

Table 1: Comparison with Other Stream Ciphers.
Algorithm Structure Key. Gen. (Cy./By.) Init. (Cy./Init.) ISE
SNOW 2.0(Ekdahl and Johansson, 2003) LFSR 4.5 937 0.440
SOBER-t32(NESSIE, 2003) LFSR 28 944 0.290
LILI-128(NESSIE, 2003) clock controlled LFSR 987 59 0.375
RC4 128-bit key (NESSIE, 2003) Table Updating 20 4680 0.018
AES 128-bit key encryption (NESSIE, 2003) - 24 689 -
K2 v2.0 (Reference) DFSR 7.5 1308 0.400
K2 v2.0 (Optimal) DFSR 5.4 1136 0.400
in the same manner. Thus, we can obtain quadratic
equations to use the relation R2
t
= Sub(R1
t−1
) be-
cause the substitution consists of the AES S-Box,
which has linearly independent quadratic equations
involving the S-Box input and output bits.
However, the substitutions that were removed in
the above attack prevent construction of the linear
equations for R1
t
and R2
t
in the real algorithm. Thus,
the attacker cannot obtain the linear equation of the
fixed values of internal memory and registers, R1
0
,
R2
0
, B
0
, B
1
, ..., B
10
, A
0
, ..., A
4
for R1
t−1
and R2
t
.
This attack is impossible even for the regular clock-
ing algorithm.
Furthermore, the attacker has to guess the clocks
of each cycle to determine the equations for a full
version of the cipher. Let M be the total number
of non-constant monomials appearing in the over-
defined system of equations, and N be the number of
equations that the attacker obtains per output of one
cycle. The computational complexity of the algebraic
attack increases 2
2
· (⌈M/N⌉ − 1) (≤ 2
160
) times
by using the dynamic feedback control mechanism.
Thus, we think the full version algorithm is secure
against an algebraic attack.
Clock Control Guessing Attack. This attack
(Zenner, 2003) is effective against bit-oriented clock
controlled stream ciphers. K2 is a word-oriented
stream cipher with a large internal state, and its non-
linear part is more complicated than existing stream
ciphers broken by the attacks. An extended attack
based on an algebraic approach was discussed by S.
Al-Hinai et. al. (Al-Hinai et al., 2006). However, it is
difficult to apply the attack when a sufficiently secure
non-linear function is used to generate the keystream.
Thus, we expect that the cipher will be secure against
such attacks.
Divide-and-Conquer Approach. The output se-
quences of FSR-A and FSR-B have good statistical
properties. Thus, we expect that divide-and-conquer
attacks for the FSRs are not feasible.
4.4 Performance Analysis
We implemented the algorithm on a PC (Pentium
4 3.2 GHz) using Intel C++ Compiler Ver.9 (for
Windows), and evaluated the performance. The re-
sults of the evaluation are shown in Table 1. “Key.
Gen.” indicates the required clock-cycles for a one-
byte keystream generation and “Init.” indicates the
required clock-cycles for one initialization, includ-
ing the initial key and IV setup. The optimal ver-
sion is optimized to produce a 128-byte keystream at
once. The performance of eSTREAM
3
candidates
is about 4–14 cycle/byte in software implementation.
The performance of K2 v2.0 is much faster than exist-
ing clock controlled stream ciphers and AES, and is
competitive against word-oriented stream ciphers. K2
v2.0 is improves the security against existing attacks
proposed for SNOW 2.0. The Inner State Efficiency
(ISE) (Zenner, 2004) of the cipher, 0.4, is sufficiently
efficient.
5 CONCLUSION
This paper proposed a new design for a stream cipher,
which is a word-oriented stream cipher using dynamic
feedback control. The stream cipher K2 v2.0 is secure
against several different types of attacks, and it of-
fers high-performance encryption and decryption for
software implementations. Furthermore, the design
of K2 v2.0 is considered security against existing at-
tacks on SNOW 2.0. We believe that the dynamic
feedback control mechanism is potentially effective
against several different types of attacks, not only ex-
isting attacks but also novel attacks.
REFERENCES
Al-Hinai, S., Batten, L., Colbert, B., and Wong, K. (2006).
Algebraic attacks on clock-controlled stream ciphers.
3
eSTREAM Project, http://www.ecrypt.eu.org/stream/
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL
211

In Proc. of ACISP 2006, LNCS, volume 4058, pages
1–16. Springer Verlag.
Babbage, S. and Dodd, M. (2005). The stream ci-
pher MICKEY-128 2.0. Article for eSTREAM
Project, available at http://www.ecrypt.
eu.org/stream/p2ciphers/mickey128/
mickey128\_p2.pdf.
Billet, O. and Gilbert, H. (2005). Resistance of SNOW 2.0
against algebraic attacks. In Proc. of CT-RSA 2005,
LNCS, volume 3376, pages 19–28. Springer Verlag.
Chepyzhov, V., Johansson, T., and Smeets, B. (2001). A
simple algorithm for fast correlation attacks on stream
ciphers. In Proc. of FSE’00, LNCS, volume 1978,
pages 181–195. Springer Verlag.
Courtois, N. (2005). Algebraic attacks on combiners with
memory and several outputs. In Proc. of ICISC 2004,
LNCS, volume 3506, pages 3–20. Springer Verlag.
Daemen, J. and Rijmen, V. (1998). The Design of Rijn-
dael, Information Security and Cryptography, Texts
and Monographs. Springer Verlag.
Ekdahl, P. and Johansson, T. (2000). Snow -a new stream
cipher. The NESSIE submission paper.
Ekdahl, P. and Johansson, T. (2003). A new version of the
stream cipher SNOW. In Proc. of SAC 2002, LNCS,
volume 2595, pages 47–61. Springer Verlag.
Golic, J. D. (1996). On security of nonlinear filter genera-
tors. In Proc. of FSE ’96, LNCS, volume 1039, pages
173–188. Springer Verlag.
Hong, J. and Sarkar, P. (2005). Rediscovery of time memory
tradeoffs. IACR ePrint Archive, Report 2005/090.
Jansen, C. J., Helleseth, T., and Kholosha, A. (2005).
Cascade jump controlled sequence generator and
POMARANCH stream cipher. Article for eSTREAM
Project, available at http://www.ecrypt.
eu.org/stream/p2ciphers/pomaranch/
pomaranch\_p2.pdf.
Kiyomoto, S., Tanaka, T., and Sakurai, K. (2007). A
word-oriented stream cipher using clock control.
In SASC 2007 Workshop Record, pages 260–274,
available at
http://sasc.crypto.rub.de/files/
sasc2007_record.zip
.
NESSIE (2003). Nessie final report, parformance of
optimized implementations of the nessie primitives.
NES/DOC/TEC/WP6/D21/2.
Nyberg, K. and Wallen, J. (2006). Improved linear distin-
guishers for SNOW 2.0. In Proc. of FSE 2006, LNCS,
volume 4047, pages 144–162. Springer Verlag.
Rose, G. and Hawkes, P. (1999). The t-class of sober stream
cipher. Publication Document, QUALCOMM Aus-
tralia.
Simpson, L., Dawson, E., Golic, J., and Millan, W. (2000).
LILI keystream generator. In Proc. of SAC 2000,
LNCS, volume 2012, pages 248–261. Springer Verlag.
Zenner, E. (2003). On the efficiency of the clock control
guessing attack. In Proc. of ICISC’02, LNCS, volume
2587, pages 200–212. Springer Verlag.
Zenner, E. (2004). On the role of the inner state size in
stream ciphers. Reihe Informatik 01-2004.
A MATRIX OF α
i
M
α
1
is the 32× 32 matrix over GF(2) given by
10001101100000000000000000000000
11000110010000000000000000000000
11100011001000000000000000000000
11111100000100000000000000000000
11111110000010000000000000000000
01110010000001000000000000000000
00110100000000100000000000000000
00011010000000010000000000000000
00110111000000001000000000000000
10011011000000000100000000000000
01001101000000000010000000000000
10010001000000000001000000000000
11001000000000000000100000000000
11010011000000000000010000000000
11011110000000000000001000000000
01101111000000000000000100000000
00100111000000000000000010000000
10010011000000000000000001000000
11001001000000000000000000100000
01000011000000000000000000010000
10100001000000000000000000001000
01110111000000000000000000000100
10011100000000000000000000000010
01001110000000000000000000000001
01010100000000000000000000000000
10101010000000000000000000000000
01010101000000000000000000000000
01111110000000000000000000000000
10111111000000000000000000000000
00001011000000000000000000000000
01010001000000000000000000000000
10101000000000000000000000000000
SECRYPT 2007 - International Conference on Security and Cryptography
212

M
α
2
is the 32× 32 matrix over GF(2) given by
01010010100000000000000000000000
10101001010000000000000000000000
00000110001000000000000000000000
10000011000100000000000000000000
11000001000010000000000000000000
00110010000001000000000000000000
01001011000000100000000000000000
10100101000000010000000000000000
01110011000000001000000000000000
00111001000000000100000000000000
01101111000000000010000000000000
00110111000000000001000000000000
00011011000000000000100000000000
01111110000000000000010000000000
11001100000000000000001000000000
11100110000000000000000100000000
00100110000000000000000010000000
10010011000000000000000001000000
11101111000000000000000000100000
01110111000000000000000000010000
10111011000000000000000000001000
01111011000000000000000000000100
10011011000000000000000000000010
01001101000000000000000000000001
01011101000000000000000000000000
00101110000000000000000000000000
01001010000000000000000000000000
00100101000000000000000000000000
00010010000000000000000000000000
01010100000000000000000000000000
01110111000000000000000000000000
10111011000000000000000000000000
M
α
3
is the 32× 32 matrix over GF(2) given by
10011010100000000000000000000000
01001101010000000000000000000000
00111100001000000000000000000000
10000100000100000000000000000000
11000010000010000000000000000000
11100001000001000000000000000000
01101010000000100000000000000000
00110101000000010000000000000000
00000010000000001000000000000000
00000001000000000100000000000000
10000010000000000010000000000000
01000011000000000001000000000000
00100001000000000000100000000000
00010000000000000000010000000000
00001010000000000000001000000000
00000101000000000000000100000000
10110010000000000000000010000000
11011001000000000000000001000000
11011110000000000000000000100000
11011101000000000000000000010000
11101110000000000000000000001000
11110111000000000000000000000100
11001001000000000000000000000010
01100100000000000000000000000001
11001101000000000000000000000000
01100100000000000000000000000000
11001101000000000000000000000000
11100110000000000000000000000000
00111110000000000000000000000000
11010010000000000000000000000000
11101001000000000000000000000000
11110100000000000000000000000000
00110111000000000000000000000000
10011011000000000000000000000000
B TEST VECTOR
A test vector for K2 is shown in this section.
Initial Key (128 bits):
IK
0
=0x00000000, IK
1
=0x00000000,
IK
2
=0x00000000, IK
3
=0x00000000
Initial Vector (128 bits):
IV
0
=0x00000000, IV
1
=0x00000000,
IV
2
=0x00000000, IV
3
=0x00000000
Keystream:
0xF871EBEF945B7272, 0xE40C04941DFF0537,
0x0B981A59FBC8AC57, 0x566D3B02C179DBB4,
0x3B46F1F033554C72, 0x5DE68BCC9872858F,
0x575496024062F0E9, 0xF932C998226DB6BA
K2: A STREAM CIPHER ALGORITHM USING DYNAMIC FEEDBACK CONTROL
213
