EFFICIENT LARGE-SCALE DISTRIBUTED KEY GENERATION
AGAINST BURST INTERRUPTION
∗
Jheng-Ru Ou, Shi-Chun Tsai and Wen-Guey Tzeng
Dept. Computer Science, National Chiao Tung University, Taiwan
Keywords:
Distributed key generation, secret sharing, cryptographic protocol.
Abstract:
A distributed key generation scheme allows the key servers to distributively share a secret key and then com-
pute the corresponding public key. Canny and Sorkin (Canny and Sorkin, 2004) proposed a probabilistic
threshold distributed key generation scheme that is suitable for the case that the number of key servers is large.
The communication cost of their scheme is much less than that of previous schemes. Nevertheless, it is pos-
sible to improve their scheme in some aspects. In this paper we employ the randomness technique to cope
with some problems encountered by their scheme. Our contribution is twofold. Firstly, our scheme is secure
against a large cluster of dishonest key servers. Secondly, our scheme has better performance in some aspects.
We support this point by a series of simulation experiments. As a result, our scheme and Canny and Sorkin’s
scheme can be used in different situations.
1 INTRODUCTION
The security of a cryptographic scheme usually relies
on protecting a secret key. One way to protect such
a key is to distribute it to a set of key servers such
that each key server holds a key share. Key sharing
not only enhances key protection, but also provides a
robustness property for the secret key. For example, in
a threshold key sharing scheme, a set of key servers
over a threshold number can recover the secret key.
Even though some servers do not work, the system
works.
A distributed key generation scheme allows the
key servers to distributively share a secret key and
then compute the corresponding public key. In this
paper we focus on discrete logarithm-based thresh-
old distributed key generation schemes, in which the
secret key is x and the public key is y = g
x
mod
p. Almost all threshold distributed key genera-
tion schemes use secret sharing schemes as build-
ing blocks. Each key server runs a secret sharing
scheme to share its chosen secret to other key servers.
∗
Supported in part by NSC projects 94-2213-E-009-110
and 95-2221-E-009-031, and Taiwan Information Security
Center at NCTU (TWISC@NCTU).
Shamir (Shamir, 1979) proposed the first threshold
secret sharing scheme based on polynomial interpo-
lation. Feldman (Feldman, 1987) added verification
of secret shares (verifiable secret sharing, VSS) to
Shamir’s scheme. Pedersen (Pedersen, 1991a) further
improved the scheme by making the secret shares un-
conditionally secure.
Based on his verifiable secret sharing scheme,
Pedersen (Pedersen, 1991b) proposed a threshold dis-
tributed key generation scheme with some important
properties that a threshold distributed key generation
scheme should have. Gennaro et al. (Gennaro et al.,
1999) found that an adversary can bias the distribu-
tion of the generated secret key by a subtle maneuver.
They then gave a formal definition and proposed a se-
cure scheme. Chu and Tzeng (Chu and Tzeng, 2002)
further pointed out that dishonest key servers should
not obtain valid key shares to avoid abuse. Canny and
Sorkin (Canny and Sorkin, 2004) proposed a prob-
abilistic threshold distributed key generation scheme
that is suitable for the case that the number n of in-
volved key servers is large, for example, in the level
of hundreds or thousands. The main merit of their
scheme is that the total number of communications
between key servers is greatly reduced from O(n
2
)
197
Ou J., Tsai S. and Tzeng W. (2007).
EFFICIENT LARGE-SCALE DISTRIBUTED KEY GENERATION AGAINST BURST INTERRUPTION.
In Proceedings of the Second International Conference on Security and Cryptography, pages 197-203
DOI: 10.5220/0002122201970203
Copyright
c
 SciTePress

to O(nl/ε
2
), where l and ε are security and robust-
ness parameters, respectively. Nevertheless, it is pos-
sible to improve their scheme in some aspects. Since
the arrangement of key servers is very regular, the
scheme is vulnerable to a large cluster of dishonest
key servers. If the DoS attack occurs to block a cluster
of honest key servers from connecting to Internet, the
execution of the scheme would fail. See Section 2.2
for the details.
In this paper we employ the randomness technique
to cope with the problems encountered by Canny and
Sorkin’s scheme. We assign non-zero values to ran-
dom entries, while Canny and Sorkin’s scheme as-
signs non-zero values to fixed entries. Our contribu-
tion is twofold. Firstly, our scheme is secure against
a large cluster of dishonest key servers. Secondly,
its performance is better than Canny and Sorkin’s
method in some aspects. We support this point by
a series of simulation experiments. As a result, our
scheme and Canny and Sorkin’s scheme can be used
in different situations.
2 PRELIMINARY
Let p = 2q+1 be a large prime, where q is also prime.
Let G
q
be the subgroup of quadratic residues in Z
∗
p
and g and h be generators of G
q
. Hereafter, the oper-
ations used in exponents of g and h are over Z
q
. As-
sume that there are n key servers S
1
,S
2
,. ..,S
n
, and
the threshold is t, where t ≤ n ≪ q. A bold character
is either a matrix, like E, or a vector, like a
i
,
A probabilistic threshold distributed key genera-
tion (PTDKG) scheme consists of three stages: setup,
key share establishment and public key computation.
A PTDKG scheme should satisfy the following con-
ditions.
Definition 1 An (α, β,δ)-PTDKG scheme should sat-
isfy the following conditions:
C1. The key shares of any subset of key servers define
the same secret key x, or not at all.
C2. Any number of βn key servers can recover the se-
cret key x with probability 1− δ at least.
C3. The secret key x is uniformly distributed in Z
q
.
S1. Any adversary who controls probabilistically up
to αn key servers cannot get any information
about the secret key x except the information com-
puted from the public key y directly.
In condition S1, it is necessary to assume that the
adversary randomly picks the controlled key servers.
Otherwise, if the adversary chooses the controlled key
servers, he can choose those that communicate with
the key server S
i
and gets the secret share of S
i
. Thus,
α should be less than r
i
/n, where r
i
is the number
of key servers that communicate with S
i
, 1 ≤ i ≤ n. If
we want smaller r
i
(communication cost), the security
threshold is smaller.
A typical key share establishment stage consists
of two sub-stages:
1. Each key server runs a secret sharing scheme to
share its chosen secret to other key severs.
2. Each key server combines the received secret
shares to form its key share.
In the first sub-stage, dishonest key servers are de-
tected and excluded. In the second sub-stage, the re-
mained honest key servers compute their key shares,
which define a unique secret key.
In the following two subsections, we introduce
conventional and Canny and Sorkin’s approaches for
the key share establishment stage.
2.1 Conventional Approaches
We first use the matrix representation to explain
Shamir’s secret sharing scheme. It corresponds to a
t × n-dimensional evaluation matrix:
E =





1 1 ·· · 1
1 2 ·· · n
.
.
.
.
.
.
.
.
.
.
.
.
1 2
t−1
·· · n
t−1





.
For key share establishment, each key server
S
i
,1 ≤ i ≤ n, does the following:
1. Choose a random t-dimensional (secret) vector
a
i
= [a
i,1
a
i,2
·· · a
i,t
].
2. Compute s
i
= a
i
E = [s
i,1
s
i,2
·· ·s
i,n
]. The opera-
tions are over Z
q
.
3. Send s
i, j
to the key server S
j
, 1 ≤ j 6= i ≤ n.
4. Exclude dishonest key servers and compute a key
share x
i
from the received s
i, j
, 1 ≤ j ≤ n.
In the above the verification messages and steps
are ignored for simplicity. Let H ⊆ {S
1
,S
2
,. ..,S
n
}
be the set of honest key servers established in the key
share establishment stage. Each key server S
j
in H
computes its key share
x
j
=
∑
i∈H
s
i, j
.
The secret key defined by the key shares of the key
servers in H is
x =
∑
i∈H
a
i,1
.
Since s
i
= a
i
E, we have
(
∑
i∈H
a
i
)E =
∑
i∈H
s
i
= [x
1
x
2
·· · x
n
].
SECRYPT 2007 - International Conference on Security and Cryptography
198

For A = {S
i
1
,S
i
2
,. ..,S
i
r
}, let E
A
be the matrix
with the columns i
1
,i
2
,. ..,i
r
of E. For example,
E
{S
1
,S
3
,S
4
}
is a t × 3-dimensional matrix that has
columns 1, 3 and 4 of E. A set T of key servers from
H can recover the secret key x if and only if E
T
has
the full rank, i.e., rank(E
T
) = t. We can solve x by se-
lecting t independent columns E
T
′
from E
T
, T
′
⊆ T,
and compute
∑
i∈H
a
i
= (
∑
i∈H
s
i
)
T
′
(E
T
′
)
−1
. (1)
Since any t rows of E form a Vandermonde matrix,
these rows are independent and any t key servers can
recover the secret key x, which is the first entry of
∑
i∈H
a
i
. Any set of less than t key servers cannot
compute the secret key x. Thus, the above defines a
((t − 1)/n,t/n,0)-PTDKG scheme.
One disadvantage of the above method is that each
key server S
i
has to communicate with each other key
server. The total number of communications between
the key servers is O(n
2
), which shall entail heavy net-
work overhead when n is large.
Distributed key generation schemes based on
Feldman’s and Pedersen’s verifiable secret sharing
schemes are similar except that the received shares of
each key server are verifiable (Feldman, 1987; Peder-
sen, 1991b).
2.2 Canny and Sorkin’s Approach
The idea of Canny and Sorkin to reduce the commu-
nication cost is to make s
i
very sparse by choosing an
appropriate E. For a zero entry s
i, j
, the key server S
i
need not send s
i, j
to the key server S
j
. By this, the
communication cost from S
i
to S
j
is saved. If s
i
is
very sparse, the communication cost from S
i
to other
key servers S
j
is much reduced.
Let E be a t × n-dimensional evaluation matrix
with a band of non-zero entries as follows, where ⋆
means a random number in Z
q
, which is non-zero
overwhelmingly:
E =










⋆ ⋆ ⋆ ⋆ 0 0 0 ·· · 0 0 0
0 0 ⋆ ⋆ ⋆ ⋆ 0 ·· · 0 0 0
0 0 0 0 ⋆ ⋆ ⋆ ·· · 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 0 0 0 ·· · 0 0 0
0 0 0 0 0 0 0 ·· · ⋆ 0 0
0 0 0 0 0 0 0 ·· · ⋆ ⋆ ⋆










Let l be the width of the band and f be the offset of the
band between two consecutive rows. For example, the
above band matrix has l = 4 and f = 2. In the scheme,
a dealer chooses E and publishes it. Each key sever S
i
chooses a t-dimensional block vector
a
i
=

0 ··· 0 a
i, j
a
i, j+1
·· · a
i, j+k−1
0 ··· 0

where j is a pre-determined index and k is the block
width. The vector s
i
= a
i
E has only (k− 1) f + l non-
zero entries. The key server S
i
need send non-zero
share s
i, j
to the key servers S
j
. With fixed t and n, we
can make (k− 1) f + l small by tuning parameters k, l
and f.
Canny and Sorkin’s PTDKG (called CS-PTDKG
hereafter) scheme is (1/ f − ε,1/ f + ε, δ), for some
small ε and δ, 0 < ε,δ < 1. Overall, their method
needs n((k−1) f +l)) node-to-node communications,
while most previous methods need n(n− 1) node-to-
node communications. They suggest that l = O(logn)
and k = l/(2ε
2
). This saves quite a lot of communi-
cations between key servers overall when n is large.
We note that E and a
i
is very regular and this reg-
ularity makes the system vulnerable to burst interrup-
tion. For example, if a burst interruption keeps l con-
secutive key servers from participating the scheme,
the scheme does not work even though the number
n − l of alive key servers is much larger than βn =
(1/ f + ε)n.
3 OUR CONSTRUCTION
We employ the randomness technique to cope with
the problem of burst interruption. We choose E and
a
i
randomly such that it is more robust against burst
interruption. To see this, if l consecutive key servers
cannot participate, the rest key servers can compute
the secret key with high probability.
For each row of E, we randomly choose l entries
and assign random values in Z
q
to them. For example,
the following E has t = 3, n = 5, and l = 2:
E =


0 1 0 0 5
3 0 2 0 0
0 4 0 3 0


. (2)
Each key server S
i
,1 ≤ i ≤ n, randomly chooses k en-
tries of a
i
and assigns random values in Z
q
to them.
We see that s
i
= a
i
E has kl non-zero entries at most.
Although the number of non-zero entries is more than
(k − 1) f + l in the CS-PTDKG scheme if k and l
are the same. We shall show that our system needs
smaller k and l to achieve the same level of robust-
ness in simulation.
Before presenting our scheme, we need to discuss
some theoretical problems concerning the feasibility
of our construction. The framework is to consider
the probability that E
′
, which is obtained from E by
deleting some columns randomly, has the full rank.
If rank(E
′
) = t, the key shares of honest key servers
define the secret key uniquely.
EFFICIENT LARGE-SCALE DISTRIBUTED KEY GENERATION AGAINST BURST INTERRUPTION
199

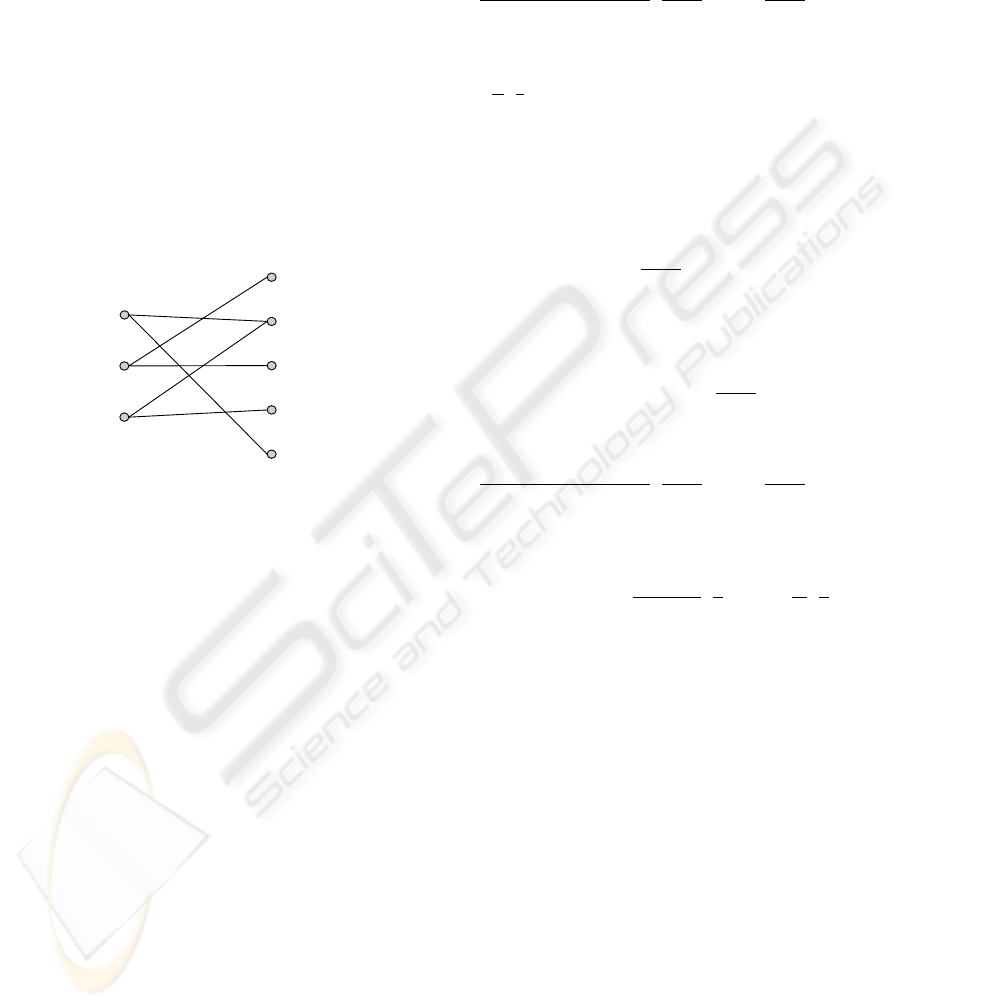
First, the following are some terminologies about
graphs. Let U and V be two sets of vertices. A graph
G = (U,V,E) is bipartite if the edge set E ⊆ U × V,
that is, the vertices in U (and V) are not connected.
A bipartite graph G = (U,V, E) is left l-regular if all
vertices in U have degree l. A perfect matching for a
bipartite graph G = (U,V,E) with |U| ≤ |V| is a set
of edges M ⊆ E with |M| = |U| such that every vertex
x ∈ U is incident to one edge in M and every vertex
y ∈ V is incident to at most edge in M.
We consider E as the matrix representation of a bi-
partite graph G = (U,V,E), where each row is a ver-
tex in U, each column is a vertex in V and (u,v) ∈ E
if the (u,v)-entry of E is non-zero. Thus, |U| = t and
|V| = n. For example, the bipartite graph correspond-
ing to the matrix in Equation (2) is:
u
1
u
2
u
3
v
1
v
2
v
3
v
4
v
5
It is left l-regular since every vertex u ∈ U has degree
l. We see that M = {(u
1
,v
5
), (u
2
,v
1
), (u
3
,v
2
)} is a
perfect matching for the graph.
The property of the full rank of E is related to
perfect matching of G = (U,V, E), |U| ≤ |V|. As-
sume that M ⊆ E is a perfect matching of G. We can
use the matching edge (u,v) ∈ M as the pivot entry
(u,v) of E to eliminate non-zero entries in column
v. Furthermore, since the values in non-zero entries
are randomly selected from a very large set Z
q
, it is
very unlikely that the elimination process by a pivot
would cause another pivot to be zero. Therefore, the
t columns associated with the perfect matching M are
independent. We would say that E has the full rank
t if and only if G has a perfect matching. The crite-
ria for a bipartite graph to have a perfect matching is
known as Hall’s lemma.
Lemma 1 (Hall) A bipartite graph G = (U,V,E) has
a perfect matching fromU to V if and only if for every
subset S ⊆ U, |Γ(S)| ≥ |S|, where Γ(S) is the set of S’s
neighbor vertices in V.
We show that the probability that a random left l-
regular bipartite graph has a perfect matching is close
to 1. In the following two theorems, we allow multi-
ple edges in bipartite graphs for a simpler analysis. If
no multiple edges are allowed, which is like our con-
struction, the probability of forming a perfect match-
ing is higher. This means that our construction is bet-
ter than the analyzed one.
Theorem 1 For appropriate positive integers t,l and
n such that, for 3 ≤ j ≤ t,
j( j− 1)
(t − j + 1)(n− j + 2)
(
j− 2
j− 1
)
( j−1)l
(
n
j− 1
)
l
≥ 1.
The probability that a random left l-regular bipar-
tite graph G = (U,V,E) has a perfect matching is
1 −
t
3
2
(
1
n
)
2l−1
at least , where |U| = t, |V| = n and
t ≤ n.
Proof 1 We compute the probability that the condi-
tion in Hall’s lemma is not satisfied. For a subset
S ⊆ U of j vertices and a subset T ⊆ V of j − 1 ver-
tices, the probability that all edges from S hit into the
set T is
(
j− 1
n
)
jl
.
The probability that there is a subset S ⊆ U of j ver-
tices whose edges hit within a subset of fewer than j
vertices of V is at most
p
j
=

t
j

n
j− 1

(
j− 1
n
)
jl
.
Since, for 3 ≤ j ≤ t, p
j−1
/p
j
=
j( j− 1)
(t − j + 1)(n− j + 2)
(
j− 2
j− 1
)
( j−1)l
(
n
j− 1
)
l
≥ 1,
the probability that a left l-regular random bipartite
graph does not satisfy Hall’s lemma is at most
t
∑
j=2
p
j
≤ (t − 1)p
2
=
t(t − 1)
2
2
(
1
n
)
2l−1
<
t
3
2
(
1
n
)
2l−1
.
Thus, the theorem holds.
We notice that the probability can be made arbitrarily
small even with rather small l since l is in the expo-
nent of 1/n and n is large.
Now, we consider the recoverability of the secret
key after the key share establishment stage. After dis-
honest and unavailable key servers are discarded, a set
H of honest key servers is formed. The secret key is
computed from the key shares of the key servers in H.
The key servers in H can recover the secret key if and
only if E
H
has the full rank t, as explained in Equa-
tion (1). Assume that H is randomly selected from
{S
1
,S
2
,. .. ,S
n
}. The probability that E
H
has the full
rank depends on the size of H. We show that as long
as H is not too small, the probability is close to 1.
Let V
′
(that is, the set H of honest key servers) be
a subset of V by randomly deleting m vertices from
V. Then, the bipartite graphy G
′
= (U,V
′
,E|
U∪V
′
)
has a perfect matching with an overwhelming proba-
bility with proper parameters, where E|
U∪V
′
is the set
of edges incident to vertices in U ∪V
′
.
SECRYPT 2007 - International Conference on Security and Cryptography
200

Theorem 2 For appropriate positive intgers t, l,m
and n such that, for 3 ≤ j ≤ t,
j( j− 1)
(t − j + 1)(n− m− j + 2)
·
(
j− 2+ m
j− 1+ m
)
( j−1)l
(
n
j− 1+ m
)
l
≥ 1.
Let G = (U,V, E) be a left l-regular random bipar-
titate graph. After deteting random m vertices from
V, the probability that the remainded bipartite graph
has a perfect matching is 1−(n−m)
t(t−1)
2
2
(
m+1
n
)
2l
at
least , where |U| = t, |V| = n and t ≤ n.
Proof 2 LetV
′
be the subset ofV after deleting m ver-
tices, where |V
′
| = n
′
= n− m. An edge from a vertex
inU that hits a vertex inV −V
′
makes no contribution
to Hall’s lemma. For a subset S ⊆ U of j vertices and
T ⊆ V
′
of j − 1 vertices, the probability that Hall’s
lemma does not hold on S to T is
(
j− 1+ m
n
)
jl
.
Thus, the probability that there is a subset of S ⊆ U of
j vertices whose edges hit a subset of fewer than j− 1
vertices in V
′
or V −V
′
is at most
p
j
=

t
j

n− m
j− 1

(
j− 1+ m
n
)
jl
Since
p
j−1
p
j
=
j( j− 1)
(t − j + 1)(n− m− j + 2)
·
(
j− 2+ m
j− 1+ m
)
( j−1)l
(
n
j− 1+ m
)
l
≥ 1,
we have
t
∑
j=2
p
j
≤ (t − 1)p
2
=
t(t − 1)
2
2
(n− m)(
m+ 1
n
)
2l
,
which is an upper bound for the proability that Hall’s
lemma fails.
3.1 Our Distributed Key Generation
Scheme
The structure of our scheme is based on Gennaro et
al.’s study on secure distributed key generation (Gen-
naro et al., 1999). Their scheme is secure against the
attack of skewing the secret key distribution by dis-
honest key servers. Note that the key shares of their
scheme are unconditionally secure.
At beginning, a dealer chooses a t ×n-dimensional
evaluation matrix E and publishes it in a public bul-
letin board. Our distributed key generation scheme is
as follows:
Setup
:
1. A dealer does:
(a) Select a large prime p = 2q+ 1, where q is also
prime.
(b) Compute generators g and h of G
q
, where
G
q
= {a
2
| a ∈ Z
∗
p
} is the subgroup of quadratic
residues of Z
∗
p
.
(c) Choose a t × n-dimensional evaluation matrix
E such that each row has l non-zero entries.
Key share establishment
:
1. Each key server S
i
does the following:
(a) Select two t-dimensional vectors a
i
and a
′
i
which each consists of k non-zero random en-
tries. The non-zero entries are in the same in-
dexes of a
i
and a
′
i
.
(b) Compute s
i
= a
i
E, s
′
i
= a
′
i
E and the set of his
communication key servers Q
i
= { j | s
i, j
6= 0∨
s
′
i, j
6= 0}.
(c) Send s
i, j
and s
′
i, j
to key server S
j
via a secure
channel, j ∈ Q
i
.
(d) Broadcast C
i, j
= g
a
i, j
h
a
′
i, j
mod p, 1 ≤ j ≤ t, to
all the key servers in Q
i
.
2. Each key server S
j
does the following:
(a) Check validity of the received shares, for each
i, j ∈ Q
i
,
g
s
i, j
h
s
′
i, j
≡
t
∏
k=1
C
E
k, j
i,k
(mod p). (3)
If the check fails for i, S
j
broadcasts a com-
plaint against S
i
to the key servers in Q
j
.
(b) If S
j
is complained by S
i
, it sends s
j,i
and s
′
j,i
to
the key servers in Q
j
.
The other key servers in Q
j
check validity of
s
j,i
and s
′
j,i
by Equation (3).
If S
j
fails the test, it is marked as ”dishonest”
by the key servers in Q
j
.
3. Each key server S
j
builds a set H of honest key
servers and sets his key share as
x
j
=
∑
i∈H, j∈Q
i
s
i, j
mod q,
which is the jth entry of (
∑
i∈H
a
i
)E. Note that the
secret key is
x = (
∑
i∈H
a
i
) ·
~
1,
where
~
1 = [1 1 ·· · 1].
Public-key computation:
1. Each key server S
i
∈ H broadcasts A
i,k
= g
a
i,k
mod
p, 1 ≤ k ≤ t, to the key servers in H.
EFFICIENT LARGE-SCALE DISTRIBUTED KEY GENERATION AGAINST BURST INTERRUPTION
201

2. Each key server S
j
in Q
i
checks validity of A
i,k
by
verifying whether
g
s
i, j
≡
t
∏
k=1
A
E
k, j
i,k
(mod p). (4)
If the check fails, S
j
broadcasts a compliant
against S
i
and sends s
i, j
and s
′
i, j
to the key servers
in Q
i
.
3. If S
i
is ever complained, all the key servers in Q
i
reconstruct a
i
by solving s
i
= a
i
E and compute
correct A
i,k
, 1 ≤ k ≤ t.
4. Then, each key server in H computes the public
key as
y =
∏
i∈H
t
∏
j=1
A
i, j
mod p = g
(
∑
i∈G
a
i
)·
~
1
mod p.
Secret key recovery
: Note that in some situations, we
don’t need to recover the secret key x to finish a task.
Only each S
i
computes a partial result from its key
share x
i
.
1. Let T be the set of shown-up key servers in H. If
E
T
is full-ranked, solve
∑
i∈H
a
i
by the system of
equations
(
∑
i∈H
a
i
)E
T
=
∑
i∈H
s
i
.
2. The secret key is x =
∑
i∈H
a
i
·
~
1.
3.2 Analysis
The correctness and security of our scheme is shown
in the following theorem.
Theorem 3 Assume that n,t,l, and m satisfy the con-
dition in Theorem 2. The scheme in Section 3.1 is a
secure (
1
l
− ε,1 −
m
n
,(n − m)
t(t−1)
2
2
(
m+1
n
)
2l
)-PTDKG
scheme for some small ε, 0 < ε < 1.
Proof 3 (Sketch) Correctness follows from the results
of Gennaro et al. (Gennaro et al., 1999) almost in the
same way.
The bounds β = 1 − m/n and δ = (n − m)(t(t −
1)
2
/2)((m+ 1)/n)
2l
are from Theorem 2 directly. For
α = 1/l − ε, each Q
i
contains kl key servers at most.
Any adversary who controls up to a random fraction
α of them contains less than k dishonest key servers
in Q
i
in average. Since there are k unknown entries
in each a
i
, the adversary who controls less than k key
servers in Q
i
cannot know the information about a
i
.
For the uniform distribution of x over Z
q
, we con-
struct a simulator for the scheme. The details are de-
ferred to the full paper.
4 EXPERIMENTS AND
COMPARISON
We first analyze the probability that the full rank is
achieved after deleting about a half of key servers.
Recall that l is the band of E, f is the offset, and t
is the number of rows.
The choice of parameters affects the communi-
cation cost of the scheme. We discuss the param-
eters first. For the CS-PTDKG scheme, due to the
arrangement of E, the number of rows is fixed to
t = (n− l)/ f . On allowing n(1/2− ε) dishonest key
servers (eg., ε = 1/10), Canny and Sorkin suggests
f = 2, l = 17logn and t = (n − 17logn)/2. Theo-
retically, the probability of achieving the full rank is
O(n
−2
).
For our PTDKG scheme, we shall do some simu-
lation experiments to obtain appropriate l
′
on the con-
dition that the probability of achieving the full rank is
the same as that of the CS-PTDKG scheme.
We take n = 1000 and delete about m = 500 dis-
honest key servers randomly. We consider different
offsets (f = 2, f = 3, and f = 4) for the CS-PTDKG
scheme. The results are shown in Figures 1-3. In each
figure, the y-axis indicates the probability of achiev-
ing the full rank and the x-axis indicates the number l
of non-zero entries in each row of E. The probability
is computed by randomly sampling 500 key servers
as ”dishonest” many times. We summarize the com-
parison results in Table 1 on 90% of achieving the full
rank. From the table, we can see that the number l
′
of
non-zero entries in each row of our E is much smaller
than that (l) of the CS-PTDKG scheme.
Table 1: Comparison of l with 90% of achieving the full
rank. There are n = 1000 key servers and m=500 of them
are dishonest.
t = 408 t = 318 t = 242
( f = 2) ( f = 3) ( f = 4)
CS-PTDKG l = 185 l = 45 l = 33
Ours l
′
= 14 l
′
= 11 l
′
= 8
Communication cost. The total communication
cost of our scheme is k
′
l
′
n and that of the CS-PTDKG
scheme is ((k − 1) f + l)n. If we want our scheme
to have the same communication cost as that of the
CS-PTDKG scheme, we set k
′
= ((k−1) f + l)/l
′
, the
number of non-zero entries in each a
i
of our scheme.
SECRYPT 2007 - International Conference on Security and Cryptography
202

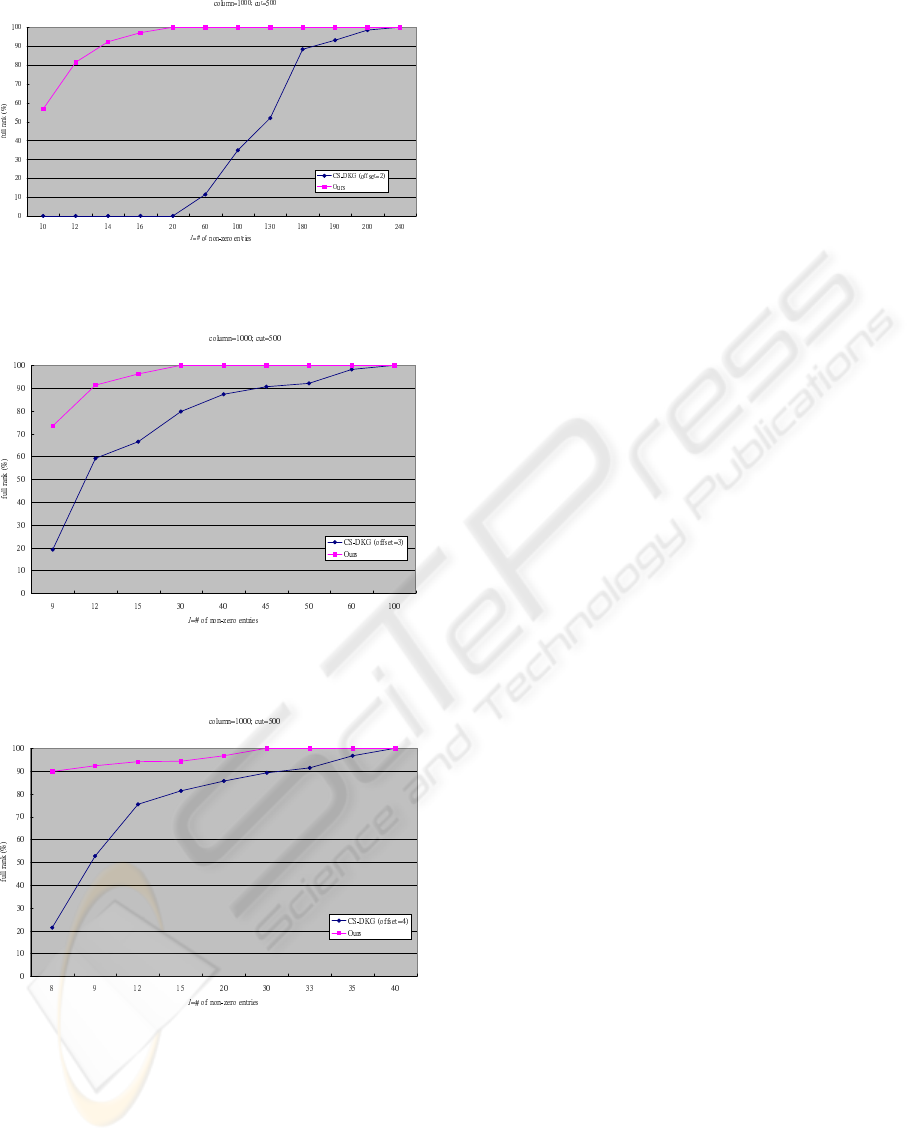
Figure 1: Probability of achieving the full rank for different
l, when f = 2.
Figure 2: Probability of achieving the full rank for different
l, when f = 3.
Figure 3: Probability of achieving the full rank for different
l, when f = 4.
5 DISCUSSION
Our scheme and the CS-PTDKG scheme have dif-
ferent security parameters. For ours, α = 1/l
′
− ε
and β = 1 − m/n. For the CS-PTDKG scheme, α =
1/ f − ε and β = 1/ f + ε. These two set of param-
eters can be used for different situations. For exam-
ple, if the number of dishonest key server is relatively
small (about one in l
′
key servers), our scheme is suit-
able. Since we are dealing with a large number of
key servers, a small percent of dishonest key servers
is very likely. Our β is adjustable under some con-
straints. If larger β is desirable, our scheme provides
such choice.
REFERENCES
Canny, J. and Sorkin, S. (2004). Practical large-scale dis-
tributed key generation. In Proceedings of Advances
in Cryptology - EUROCRYPT ’04, volume 3027 of
LNCS, pages 138–152. Springer-Verlag.
Chu, C.-K. and Tzeng, W.-G. (2002). Distributed key gener-
ation as a component of an integrated protocol. In Pro-
ceedings of the 4th Information and Communications
Security - ICICS ’02, volume 2513 of LNCS, pages
411–421. Springer-Verlag.
Feldman, P. (1987). A practical scheme for non-interactive
verifiable secret sharing. In 28th Annual Symposium
on Foundations of Computer Science (FOCS), pages
427–437. IEEE.
Gennaro, R., Jarecki, S., Krawczyk, H., and Rabin, T.
(1999). Secure distributed key generation for discrete-
log based cryptosystems. In Proceedings of Advances
in Cryptology - EUROCRYPT ’99, volume 1592 of
LNCS, pages 295–310. Springer-Verlag.
Pedersen, T. P. (1991a). Non-interactive and information-
theoretic secure verifiable secret sharing. In Proceed-
ings of Advances in Cryptology - CRYPTO ’91, vol-
ume 576 of LNCS, pages 129–140. Springer-Verlag.
Pedersen, T. P. (1991b). A threshold cryptosystem without a
trusted party. In Proceedings of Advances in Cryptol-
ogy - EUROCRYPT ’91, volume 547 of LNCS, pages
522–526. Springer-Verlag.
Shamir, A. (1979). How to share a secret. Communications
of the ACM, 22(11):612–613.
EFFICIENT LARGE-SCALE DISTRIBUTED KEY GENERATION AGAINST BURST INTERRUPTION
203