THE ART TO KEEP IN TOUCH
The “good use” of Lagrange Multipliers
Antoine Jonquet, Olivier Nocent
Department of Computer Science, Institute of Technology, Reims University, rue des cray`eres, 51687 Reims cedex 2, France
Yannick Remion
Department of Computer Science, Institute of Technology, Reims University, rue des cray`eres, 51687 Reims cedex 2, France
Keywords:
Physically-based animation, constraints, contact simulation.
Abstract:
Physically-based modeling for computer animation has become a wide spread framework because it allows
to produce more realistic motions in less time without requiring the expertise of skilled animators. But, a
computer animation is not only a numerical simulation based on classical mechanics since it follows a precise
story-line. One common way to define aims in an animation is to add geometric constraints. There are
several methods to manage these constraints within a physically-based framework. In this paper, we present
an algorithm for constraints handling based on Lagrange multipliers. After few remarks on the equations of
motion that we use, we present a first algorithm proposed by Platt. We show with a simple example that this
method is not reliable. Our contribution consists in improving this algorithm to provide an efficient and robust
method to handle simultaneous and antagonist constraints.
1 INTRODUCTION
For about two decades, the computer graphics com-
munity has investigated the field of physics in order
to produce more and more realistic computer anima-
tions. In fact, physically-basedmodeling in animation
allows to generate stunning visual effects that would
be extremely complex to reproduce manually. On one
hand, the addition of physical properties to 3D objects
automates the generation of motion just by specifying
initial external forces. On the other hand, physically-
based animations are even more realistic than tradi-
tional key-framed animations that require the exper-
tise of many skilled animators. As a consequence, the
introduction of physically-based methods in model-
ing and animation significantly reduced the cost and
production time of computer generated movies. But,
one main drawback of this kind of framework is that
it relies on heavy mathematics usually hard to tackle
for a computer scientist. A second main disadvantage
concerns the input of a physically-based animation:
in fact, forces and torques are not really user-friendly
since it is really difficult to anticipate a complex mo-
tion just by specifying an initial set of external forces.
A computer animation is definitely not a numer-
ical simulation because it follows a story-line. Ac-
cording to Demetri Terzopoulos (Terzopoulos et al.,
1989), an animation is simulation plus control. One
way to ensure that the objects fulfill the goals defined
by the animator is to use geometric constraints. A
constraint is an equality or an inequality that gath-
ers different parameters of the animation like the total
time elapsed, the positions or the orientations of the
moving objects. In a less general way, mechanical
simulations also benefit from the use of constraints
in order to prevent interpenetration between physical
objects for example.
There are several methods to handle constraints,
summarized in a survey paper by Baraff (Baraff,
1993). But, since our research work is mostly de-
voted to mechanical simulation, we decided to focus
on the use of Lagrange multipliers to manage the ge-
ometric constraints. In fact, numerical simulations re-
quire robust and reliable techniques to ensure that the
constraints are never violated. Moreover, with this
method we are also able to measure the amount of
strain that is necessary to fulfill a given constraint.
In this paper, we present a novel algorithm to man-
age efficiently several simultaneous active geometric
constraints. We begin by detailing the physical equa-
47
Jonquet A., Nocent O. and Remion Y. (2007).
THE ART TO KEEP IN TOUCH - The “good use” of Lagrange Multipliers.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 47-54
DOI: 10.5220/0002085000470054
Copyright
c
 SciTePress

tions that we use before presenting Platt’s algorithm
(Platt, 1992) that is the only algorithm of this type
based on lagrange multipliers. With a simple exam-
ple, we demonstrate that this algorithm is not suitable
for handling simultaneous active constraints. We then
introduce our own contribution in order to show how
to improvePlatt’s algorithm to make it reliable, robust
and efficient.
2 LAGRANGE EQUATIONS OF
MOTION
Lagragian dynamics consist in an extension of new-
tonian dynamics allowing to generate a wide range of
animations in a more efficient way. In fact, Lagrange
equations of motion rely on a set of unknowns, de-
noted as a state vector x of generalized coordinates,
that identifies the real degrees of freedom (DOF) of
the mechanical systems involved. Within this for-
malism, the DOF are not only restricted to rotations
or translations. For example, a parameter u ∈ [0, 1]
which gives the relative position of a point along a 3D
parametric curve can be considered as a single gener-
alized coordinate.
2.1 Unconstrained Motion
The evolution of a free mechanical system only sub-
ject to a set of external forces is ruled by the Lagrange
equations of motion (1).
M
¨
x = f (1)
M is the mass matrix.
¨
x is the second time deriva-
tive of the state vector. Finally, the vector f corre-
sponds to the sum of external forces. For more details
concerning this formalism, we suggest to read (Gold-
stein, 1980) and (Arnold, 1989).
2.2 Constrained Motion
By convention, an equality constraint will always be
defined as in equation (2) where E is the set of indices
of all the equality constraints.
g
k
(x) = 0 ∀k ∈ E (2)
Constraints restrict the set of reachable configura-
tions to a subspace of R
n
where n is the total number
of degrees of freedom. As mentioned before, there
exists three main methods to integrate constraints in
equation (1)
The projection method consists in modifying the
state vector x and its first time derivative
˙
x in
order to fulfill the constraint. This modification
can be performed with an iterative method like
the Newton-Raphson method (Press et al., 1992).
Even if this method is very simple and seems to
ensure an instantaneous constraint fulfillment, it
is not robust enough: indeed it can not guarantee
that the process converges in the case of simulta-
neous active constraints.
The penalty method adds new external forces, act-
ing like virtual springs, in order to minimize the
square of the constraint equation, considered as a
positive energy function. The main advantage of
this method is its compatibility with any dynamic
engine since it only relies on forces. But this
method leads to inexact constraint fulfillment, al-
lowing interpenetration between the physical ob-
jects. In order to diminish this interpenetration,
the stiffness of the virtual springs must be sig-
nificantly increased, making the numerical system
unstable.
The Lagrange method consists in calculating the
exact amount of strain, denoted as the Lagrange
multiplier, needed to fulfill the constraint. This
method guarantees that constraints are always ex-
actly fulfilled. Since the use of Lagrange multipli-
ers introduces a set of new unknowns, the equa-
tion (1) must be completed by a set of new equa-
tions, increasing the size of the initial linear sys-
tem to solve. But we consider that this method
is the only suitable to manage efficiently the geo-
metric constraints.
For all the reasons mentioned above, we choose
the Lagrange method to manage our geometric con-
straints. According to the principle of virtual work,
each constraint g
k
adds a new force perpendicular to
the tangent space of the surface g
k
(x) = 0. The La-
grange multiplier λ
k
corresponds to the intensity of
the force related to the constraint g
k
. With these new
forces, the equation (1) is modified as follows:
M
¨
x = f +
X
k∈E
λ
k
∂g
k
∂x
(3)
We add new equations to our system by calculat-
ing the second time derivativeof equation (2), leading
to equation (4).
n
X
i=1
∂g
k
∂x
i
¨x
i
= −
n
X
i,j=1
∂
2
g
k
∂x
i
∂x
j
˙x
i
˙x
j
∀k ∈ E (4)
In order to correct the numerical deviation due to
round-off errors, Baumgarte proposed in (Baumgarte,
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
48

1972) a constraint stabilization scheme illustrated by
the equation (5). The parameter τ
−1
can be seen as
the speed of constraint fulfillment.
n
X
i=1
∂g
k
∂x
i
¨x
i
= −
n
X
i,j=1
∂
2
g
k
∂x
i
∂x
j
˙x
i
˙x
j
−
2
τ
n
X
i=1
∂g
k
∂x
i
˙x
i
−
1
τ
2
g
k
(5)
When we mix the equations (1) and (5), we obtain
a linear system where the second time derivative of
the state vector x and the vector of Lagrange multi-
pliers Λ are the unknowns.

M −J
T
−J 0

¨
x
Λ

=

f
−d

(6)
J is the jacobian matrix of all the geometric con-
straints and d corresponds to the right term of equa-
tion (5).
2.3 Inequality Constraints Management
By convention, an inequality constraint will always be
defined as in equation (7) where F is the set of indices
of all the inequality constraints.
g
k
(x) ≥ 0 ∀k ∈ F (7)
For a given state vector x, we remind the follow-
ing definitions:
• the constraint is said to be violated by x when
g
k
(x) < 0. This means that the state vector x
corresponds to a non allowed configuration.
• the constraint is said to be satisfied by x when
g
k
(x) ≥ 0.
• the constraint is said to be active by x when
g
k
(x) = 0. In this case, the state vector x be-
longs to the boundary of the subspace defined by
the inequality constraint g
k
.
The management of inequality constraints is more
difficult than the management of equality constraints.
An inequality constraint must be handled only if it
is violated or active. In fact, the algorithm is a little
more complicated as we explain in the next sections.
That is why we define two subsets within F : F
+
is the set of indices of all handled inequality con-
straints and F
−
is the set of indices of ignored in-
equality constraints. Finally, we have F = F
−
∪ F
+
.
The jacobian matrix of constraints J of the equa-
tion (6) is built from all the constraints g
k
where
k ∈ E ∪ F
+
.
3 PREVIOUS WORK
Within the computer graphics community, the main
published method devoted to inequality constraints
management using Lagrange multipliers, known as
“Generalized Dynamic Constraints”, was proposed
by Platt in (Platt, 1992). In his paper, he describes
how to use Lagrange multipliers to assemble and
simulate collisions between numerical models. This
method is an extension of the work of Barzel and
Barr (Barzel and Barr, 1988) that specifies how con-
straints must be satisfied. Moreover, Platt proposes a
method to update F
+
(the set of handled inequality
constraints) during the animation. This algorithm can
be compared to classical active set methods (Bj¨orck,
1996; Nocedal and Wright, 1999).
We do not focus on collision detection that is a
problem by itself. We are aware that this difficult
problem can be solved in many ways, we encourage
the reader to refer to the survey paper by Teschner
et al. (Teschner et al., 2005). During the collision
detection stage, we assume that the dynamic engine
may rewind time until the first constraint activation
is detected. In any case, this stage ensures that con-
straints are never violated. But, it is possible that
several constraints are activated simultaneously. The
main topic of this paper is to provide a reliable algo-
rithm to handle these multiple active constraints in an
efficient way.
At the beginning of the animation, Platt populates
the set F
+
with all the active constraints.
Algorithm 1– Platt’s algorithm.
Solve equation (6) to get ¨x and Λ1
Update x and ˙x (numerical integration)2
for each k ∈ F do3
if k ∈ F
+
then4
if λ
k
≤ 0 then5
k is moved to F
−
6
else7
if g
k
(x) < 0 then8
g
k
is moved to F
+
9
For each time step, according to algorithm 1, we
solve equation (6) and update the state vector in order
to retrieve new positions and velocities at the end of
the current time step. We then check the status of each
inequality constraint. If a constraint g
k
is active, it is
still handled until its Lagrange multiplier is negative
or null, that is to say that the Lagrange multiplier cor-
responds to a force that prevents from deactivation.
According to the new values of the state vector x, if
THE ART TO KEEP IN TOUCH - The “good use” of Lagrange Multipliers
49

the previously inactive constraint g
k
is now violated
(g
k
(x) < 0), the constraint must be added to F
+
in
order to prevent the system to entering in such a con-
figuration.
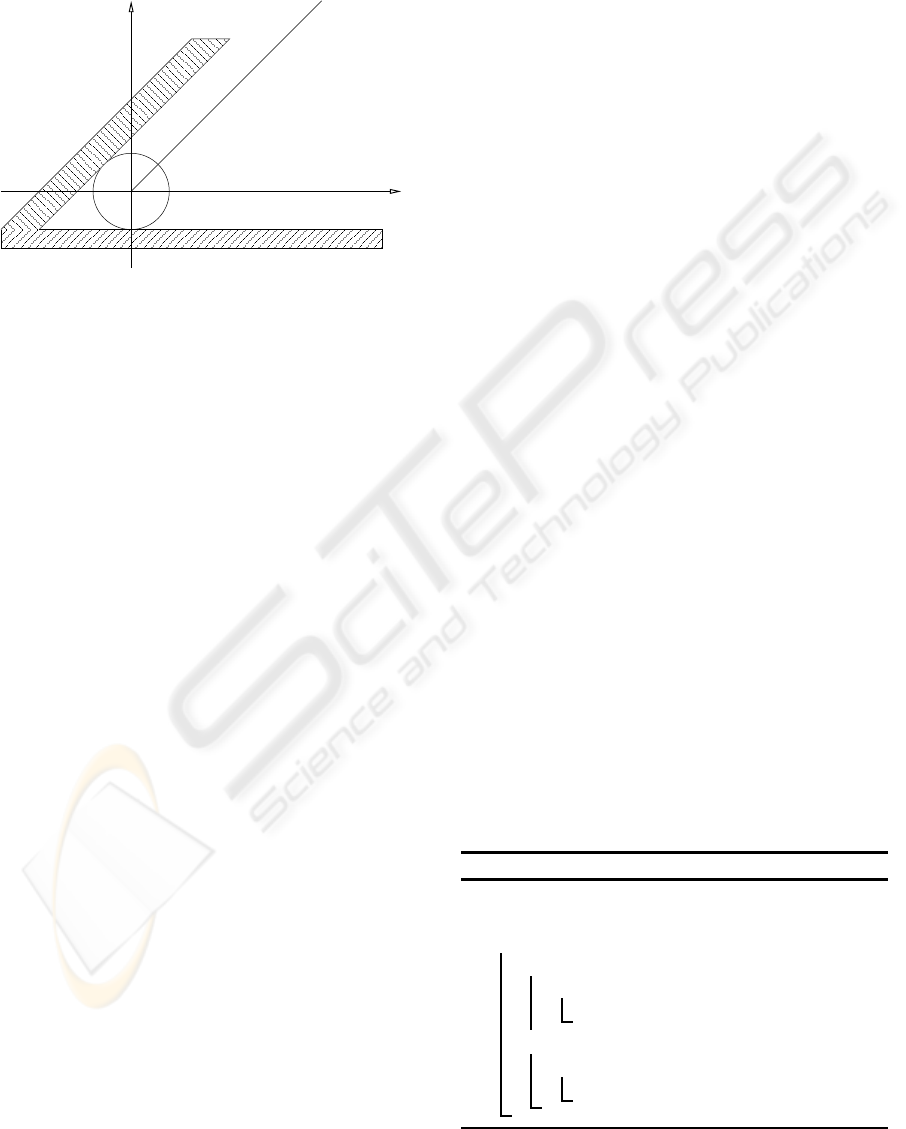
y
x
y=0
x−y=0
Figure 1: A simple example with two simultaneous active
constraints.
Even if this algorithm seems to give a reliable so-
lution for inequality constraints handling, some prob-
lems remain. We set up a simple scene as in figure 1
to illustrate the insufficiencies of Platt’s method. A
particle of mass m is constrained to slide on a 2D
plane. It starts from an acute-angle corner modeled
by two linear inequality constraints g
1
(x) = x − y
and g
2
(x) = y. Finally, this particle is subject to a
single external force f = (2, −1). In this particular
case, the state vector x is composed of the 2D coordi-
nates (x, y) of the particle. According to equation (1),
the generalized mass matrix for this system is defined
by:
M =

m 0
0 m

(8)
As the geometric constraints g
1
(x) and g
2
(x) are
linear, their first and second time derivative do not
produce any deviation term defined in equation (5):
d =

0
0

(9)
According to the initial value of the state vector
x = (0, 0), the two constraints g
1
(x) and g
2
(x) are
active, so their indices are inserted in F
+
and J, the
jacobian matrix of constraints, is defined as follows:
J =

1 −1
0 1

(10)
From equations (6) (8) (9) and (10), we obtain a
linear system whose unknowns are the second time
derivative of the state vector x and the two Lagrange
multipliers λ
1
and λ
2
associated with g
1
and g
2
:



m 0 −1 0
0 m 1 −1
−1 1 0 0
0 −1 0 0






¨x
¨y
λ
1
λ
2



=



2
−1
0
0



(11)
The solutions are ¨x = (0, 0) and Λ = (−2, − 1).
Because ¨x and ¨y are null, the particle does not move
during this time step. But, since λ
1
and λ
2
are both
negative, their corresponding constraints are moved
to F
−
. This means that, for the next time step, the
system will be free of any constraints. As the force
remains constant, the next value of ¨x will be equal to
(2m
−1
, −m
−1
). These values will lead to an illegal
position of the particle, under the line y = 0.
The amount of violation of the constraint g
2
(x) =
y mainly depends on the ratio between the mass m of
the particle and the intensity of the external force f .
The section 5 offers differentresults and comparisons.
4 OUR CONTRIBUTION
4.1 A First Approach
The problem of Platt’s method relies on the fact that it
keeps inequality constraints in F
+
abusively. In fact,
the condition g
k
(x) < 0 used to populate F
+
with in-
equality constraint is not well suited and an other way
must be proposed. A solution would be to replace
the condition g
k
(x) < 0 by a violation tendency con-
dition expressed as J
k
¨x < d
k
. An active constraint
that does not fulfill the violation tendency condition
will be satisfied during the next time step and does
not have to be handled.
At the beginning of the animation, we solve equa-
tion (1) to get ¨x and we then populate the set F
+
with
the active constraints that fulfill the violation tendency
condition. It is clear that we handle less constraints
than Platt because our criteria is more restrictive.
Algorithm 2– Platt’s improved algorithm.
Solve equation (6) to get ¨x and Λ1
Update x and ˙x (numerical integration)2
for each k ∈ F do3
if k ∈ F
+
then4
if λ
k
≤ 0 then5
k is moved to F
−
6
else7
if J
k
¨x < d
k
then8
k is moved to F
+
9
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
50

We briefly verify that this algorithm gives a cor-
rect solution to our example illustrated in figure 1.
According to equation (1), ¨x = (2m
−1
, −m
−1
). The
two constraints g
1
and g
2
are active because x =
(0, 0) but only g
2
fulfills the violation tendency con-
dition as mentioned in equation (12).
J
1
¨x = 3m
−1
, g
1
is moved to F
−
J
2
¨x = −m
−1
, g
2
is moved to F
+
(12)
In this special case, equation (6) becomes:


m 0 0
0 m −1
0 −1 0




¨x
¨y
λ
2


=


2
−1
0


(13)
The solutions of the linear system (13) are ¨x =
(2m
−1
, 0) and λ
2
= 1. Finally, the particle will slide
along the x-axis without crossing the line y = 0 be-
cause the constraint g
1
that was not handle did not
introduce a false response.
This new algorithm seems to manage multiple in-
equality constraints in a good way, but we could high-
light a problem in this algorithm by using the same ex-
ample illustrated in figure 1 with a new external force
f = (−1, −2).
At the beginning, since x = (0, 0), the constraints
g
1
and g
2
are active. From equation (1), we obtain
that ¨x = (−m
−1
, −2m
−1
), and from equation (14)
that only the consraint g
2
is handled.
J
1
¨x = m
−1
, g
1
is moved to F
−
J
2
¨x = −2m
−1
, g
2
is moved to F
+
(14)
According to equation (14), we build the linear
system (15).


m 0 0
0 m −1
0 −1 0




¨x
¨y
λ
2


=


−1
−2
0


(15)
The solutions are ¨x = (−m
−1
, 0) and λ
2
= 2.
Then, after the update of x and ˙x, the particle goes
through the plane defined by the constraint g
1
and
reaches an illegal state. This is due to the fact that the
Lagrange multiplier λ
2
pushes the system in an illegal
state from the constraint g
1
point of view, which was
not previously inserted in the system 6 as its initial
tendency acceleration tends to disconnect the particle
from the x − y = 0 plane.
At the end of the step, we check inequality con-
straints for the next animation step, as λ
2
≤ 0, g
2
stays in F
+
and J
1
¨x < d
1
, then g
1
move to F
+
. So
at the next step, the linear system will be correctly
set, but it is too late since the system is already in an
illegal state.
4.2 The “Right” Algorithm
The use of the violation tendency condition J
k
¨x <
d
k
improves simultaneous active constraints man-
agement, since only the appropriate inequality con-
straints are handled by the equation (6). But we have
seen, from the previous example, that it is insufficient
to reach the accurate configuration. In fact, the con-
straints from F
+
that fulfill the violation tendency
condition will produce a vector Λ of Lagrange mul-
tipliers that prevent the system from being in an ille-
gal configuration. In the meantime, the acceleration
tendency ¨x of the system could lead to another illegal
configuration. The only way to deal with this problem
is to use the new acceleration tendencies to test if the
other active inequality constraints g
k
fulfill the viola-
tion tendency condition and have to be handled. We
then need an iterative process that computesthe accel-
eration tendencies and test for other active inequality
constraints g
k
to insert in F
+
, until the sytem reaches
the appropriate state.
We propose a simple and efficient solution to the
inequality constraints handling problem, based on the
way physicists work. At the beginning of each time
step, all active inequality constraints g
k
are detected,
and F
+
is emptied. We then begin an iterative pro-
cess that runs until there is no new insertion in F
+
.
The acceleration tendencies
¨
x are computed from
the equation (6) and the violation tendency condition
J
k
¨x < d
k
is tested on each active inequality con-
straint. For any inequality constraint g
k
that fulfills
the condition, we insert its index k in F
+
and start
another iterative step.
Algorithm 3– The right algorithm.
repeat1
Solve equation (6) to get
¨
x and Λ2
for each active constraint g
k
do3
if J
k
¨x < d
k
then4
k is moved to F
+
5
until F
+
has not been updated;6
Update x and ˙x (numerical integration)7
Since we begin with no constraints and that only
appropriate inequality constraints are inserted to F
+
during the iterative process, the last computation of
¨
x
and Λ from equation (6) will lead to an accurate con-
figuration of the system. Moreover, this process guar-
antees the convergence towards an appropriate solu-
tion as we begin from an empty F
+
and only insert
constraints in F
+
.
In a recent communication (Raghupathi and
Faure, 2006), Raghupathi presented a method also
THE ART TO KEEP IN TOUCH - The “good use” of Lagrange Multipliers
51

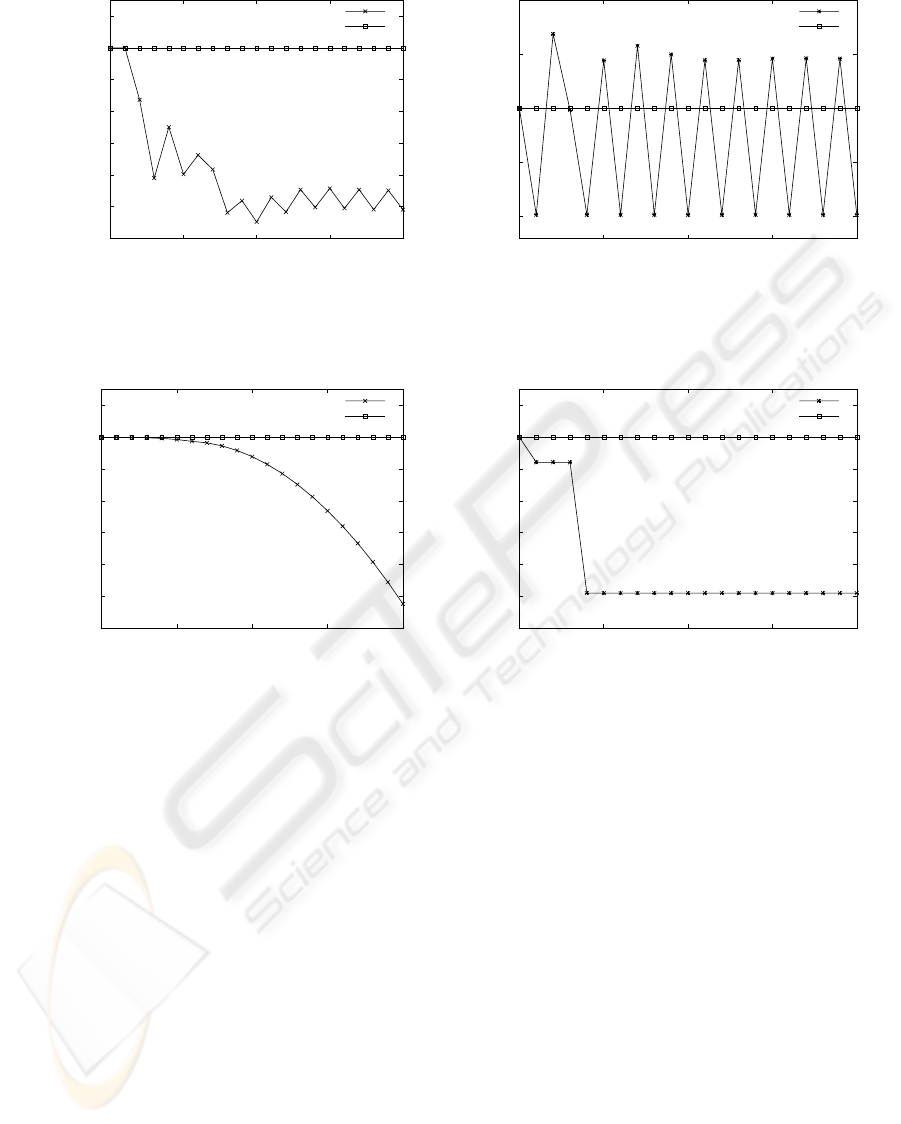
-1.2e-05
-1e-05
-8e-06
-6e-06
-4e-06
-2e-06
0
2e-06
0 0.005 0.01 0.015 0.02
position
time
Platt’s algorithm
Our algorithm
-10
-5
0
5
10
0 0.005 0.01 0.015 0.02
acceleration
time
Platt’s algorithm
Our algorithm
Figure 2: Comparison of Platt’s algorithm and our method using the example illustrated in figure 1 with a mass m = 2. The
numerical values correspond respectively to position and acceleration along the y-axis.
-0.0012
-0.001
-0.0008
-0.0006
-0.0004
-0.0002
0
0.0002
0 0.005 0.01 0.015 0.02
position
time
Platt’s algorithm
Our algorithm
-12
-10
-8
-6
-4
-2
0
2
0 0.005 0.01 0.015 0.02
acceleration
time
Platt’s algorithm
Our algorithm
Figure 3: Comparison of Platt’s algorithm and our method using the example illustrated in figure 1 with a mass m = 3. The
numerical values correspond respectively to position and acceleration along the y-axis.
based on Lagrange multipliers. For realtime consid-
erations, they do not allow the dynamic engine to
rewind time to get back to the first constraint acti-
vation. They have to manage constraints at the end
of the time step, trying to find the right accelerations
to ensure constraints fulfillement. They also confess
that this process is not guaranteed to converge in any
situation.
5 RESULTS AND COMPARISONS
We will now compare the results obtained with Platt’s
algorithm and our method, using the example illus-
trated in figure 1. Figure 2 and 3 illustrate a compari-
son of the positions and accelerations along y-axis of
a particle of mass m = 2 and m = 3 . We recall that
the inequality constraint g
2
forbids negativevaluesfor
y and that the constant force f applied to the particle
is equal (2, −1).
As shown on figure 2, Platt’s algorithm holds the
particle abusively on the corner at the first time step,
and releases it at the next time step. As a conse-
quence, the particle evolves in an illegal state during
the following steps. With a mass m = 2, the error
related to the position is less than 10
−5
with an os-
cillating acceleration (right column). But if we set
the mass m to 3, as shown in the figure 3, errors are
much more important, and the particle crosses the line
y = 0 modeled by the constraint g
2
.
As illustated, our algorithm keeps the particle
along the x-axis within a controlled numerical error
value, that is less than 10
−8
in these examples.
To illustrate multiple contact constraints, we have
set a billiard scene with 10 balls placed in triangle in a
corner and an other ball that comes to them. For each
ball, we define two inequality constraints for each side
of the corner and one inequality constraint related to
the distance between each ball. This example is fi-
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
52

nally composed of 11 balls and 77 inequality con-
straints (figure 4).
6 CONCLUSION
In this paper, we presented a novel algorithm to man-
age simultaneous inequality constraints. Among all
the existing methods to handle constraints within a
physically-based animation, we focused on the La-
grange method which provides a reliable way to en-
sure that constraints are always exactly fulfilled. But,
in the special case of several active inequality con-
straints, we have to take care on how to handle these
simultaneous constraints. Platt proposed an algorithm
based on Lagrangemultipliers but we showed that this
method is unable to solve even simple examples. We
then explained how to improve this algorithm in or-
der to propose a new reliable and efficient method for
inequality constraints handling. Beyond the example
illustrated in figure 1, we produced a short movie sim-
ulating a billiard game. Some snapshots are gathered
in figure 4.
ACKNOWLEDGEMENTS
We would like to thank the Champagne-Ardenne re-
gional council who supports this work, which is a part
of the SYS-REEDUC project.
REFERENCES
Arnold, V. I. (1989). Mathematical Methods of Classical
Mechanics, volume 60 of Graduate Texts in Mathe-
matics. Springer Verlag, New York, 2
nd
edition. 508
pages.
Baraff, D. (1993). Non-penetrating rigid body simulation.
In State of the Art Reports, Eurographics ’93.
Barzel, R. and Barr, A. H. (1988). A modeling system based
on dynamic constraints. In SIGGRAPH ’88: Pro-
ceedings of the 15th annual conference on Computer
graphics and interactive techniques, pages 179–188,
New York, NY, USA. ACM Press.
Baumgarte, J. (1972). Stabilization of constraints and inte-
grals of motion. Computer Methods in Applied Me-
chanics and Engineering, 1:1–16.
Bj¨orck,
˚
A. (1996). Numerical Methods for Least Squares
Problems. SIAM, Philadelphia, Penn.
Goldstein, H. (1980). Classical Mechanics. Addison–
Wesley, Reading, MA, U.S.A., 2
nd
edition. 672
pages.
Nocedal, J. and Wright, S. (1999). Numerical Optimization.
Springer, New York.
Platt, J. (1992). A generalization of dynamic constraints.
CVGIP: Graphical Models and Image Processing,
54(6):516–525.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vet-
terling, W. T. (1992). Numerical Recipes: The Art
of Scientific Computing. Cambridge University Press,
Cambridge (UK) and New York, 2nd edition.
Raghupathi, L. and Faure, F. (2006). QP-collide: A new ap-
proach to collision treatment. In Journ´ees du groupe
de travail Animation et Simulation (GTAS), Annual
French Working group on Animation and Simulation,
pages 91–101. Institut de Recherche en Informatique
de Toulouse.
Terzopoulos, D., Platt, J., Barr, A., Zeltzer, D., Witkin, A.,
and Blinn, J. (1989). Physically-based modeling: past,
present, and future. In SIGGRAPH ’89: ACM SIG-
GRAPH 89 Panel Proceedings, pages 191–209, New
York, NY, USA. ACM Press.
Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann,
G., Raghupathi, L., Fuhrmann, A., Cani, M.-P., Faure,
F., Magnenat-Thalmann, N., Strasser, W., and Volino,
P. (2005). Collision detection for deformable objects.
volume 24 of Computer Graphics Forum, pages 61–
81.
THE ART TO KEEP IN TOUCH - The “good use” of Lagrange Multipliers
53

Figure 4: A billiard game session illustrating our algorithm for constraints management (11 balls and 77 inequality con-
straints).
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
54