UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF

DETAIL RENDERING OF BINTREE TRIANGULATIONS

Bernd Biedermann and María Cecilia Rivara

Departamento de Ciencias de la Computación, Universidad de Chile, Chile

Keywords: Bintree Triangulations, Parallel Mesh Tessellation, Continuous Level of Detail, Uncoupled Parallel Mesh

Refinement.

Abstract: In this paper we present an uncoupled parallel technique for view dependant continuous level of detail

rendering of regular height field terrain. To this end, the terrain is globally modelled by a simple bintree

patch-based representation of right-triangles, which is adaptively divided into uncoupled meshes for parallel

processing. This is easily performed by uncoupling the mesh along the observer line. Each uncoupled mesh

is then recursively approximated to the corresponding level of detail in the terrain. Cracks are avoided by

constraining the refinement levels at the boundaries of adjacent meshes. The level of detail is created on-

the-fly with a low amount of CPU overhead, allowing a good representation of the terrain and high frames

per second performance. This implementation shows significant improvements in CPU load and frames per

second performance over the serial method when executed on machines with multiple processors.

1 INTRODUCTION

Several approaches for multiresolution

representation, adaptive modelling, level of detail

control, and real time rendering of terrain data have

been proposed and studied in the last 10 years.

Pioneer work on general mesh simplification and

multiresolution modelling are discussed in (Heckbert

and Garland 1997; Hope 1996, Hope 1998). In

particular for the multiresolution modelling of

regular height-field data, methods based on right-

triangle triangulations have been developed and

widely used. The most important of these methods

are quadtree-based and bintree-based representations

methods (Duchaineau et al, 1997; Pajarola 2002).

These methods are reported to provide a more

compact representation of the terrain, better spacial

access, faster level of detail (LOD) triangulation and

rendering and are easier to implement than more

general methods. (Pajarola 2002).

Recently (Holst and Schumann 2006) combine

the use of a reduced multiresolution hierarchy based

in (De Floriani et al 1997) together with triangle

strips for patches. They do not use right bintree

triangle representation, nor perform any parallel

work.

As a basic tool of this research we use a right-

triangle multiresolution bintree algorithm as

discussed in (Duchainean et al, 1997), which is a

special case of the longest edge refinement

algorithms for general triangulations discussed in

(Rivara 1984, Rivara 1997).

Essentially, the bintree multiresolution method

works as follows: (1) Each right triangle in the

bintree structure is splitted by its longest edge

producing right and left right-triangle children in the

bintree; (2) The adaptive local splitting of every

target triangle is performed by using a sequence of

simple mesh operations over couples of triangles of

the same bintree level, which share a longest edge in

the mesh; (3) The local splitting of a general target

triangle having a longest-edge neighbour of a

different level requires splitting propagation, which

is a particular case of the longest edge propagation

path discussed in (Rivara 1997).

When rendering terrain a specific problem arises.

The horizon of visibility is much bigger than in other

real time rendering with fixed scenes. If we were to

render every triangle at a fixed resolution we would

either have a very low quality terrain or a low

performance with a high quality terrain. To solve

this particular problem the amount of triangles close

to the observer has to be maximized and be reduced

as the distance increases. This is known as

continuous level of detail and the problem has been

333

Biedermann B. and Cecilia Rivara M. (2007).

UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE TRIANGULATIONS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 333-338

DOI: 10.5220/0002083203330338

 SciTePress

addressed by some authors with different techniques.

The core of the problem is to find a mesh for each

frame that will realistically represent the terrain. The

main problem of Continuous Level of Detail is the

huge amount of CPU overhead it produces. The

ROAM (Real Time Optimally Adapting Meshes)

algorithm (Duchaineau et al, 1997), which will be

briefly explained on this paper, is a View Dependant

Level of Detail algorithm, which adapts a mesh to an

optimal triangulation for the camera point of view.

In order to improve the adaptive terrain

rendering performance we propose a parallel

uncoupled method similar to the one discussed in

(Rivara et al, 2006) which takes advantage of the

multiprocessor architecture of current computers.

Traditional VLOD (Visual dependant Level of

Detail) algorithms run all this CPU work through

only one processor and therefore make the CPU

overhead a big problem. This can be reduced by

mesh subdivision and parallel tessellation (Padrón et

al, 2005). Most algorithms present fairly

complicated solutions for this. In this paper we

consider simple parallelization of real time view

dependant continuous level of detail.

2 BASIC TECHNIQUES USED IN

THIS PAPER

2.1 View Dependant Level of Detail

Algorithms

VLOD algorithms are designed to interactively

perform view-dependent locally adaptive terrain

meshing. They rely on a multi-resolution terrain

representation that is used to build the adaptive

terrain representation of a frame. To accomplish this,

the algorithm used in this paper is a basic

implementation of ROAM. VLOD algorithms take

the complete terrain data usually, in form of a height

field, and generate a mesh that includes every vertex

of the height map near the observer and discard

vertices as they generate mesh sections further away

from the observer. ROAM accomplishes this by

generating a mesh for each frame, while other

algorithms, like GeoMipMaps (H. de Boer, 2000

) do

this by pre-calculating a certain amount of meshes.

The advantage of dynamically generating the mesh

for each frame is that the representation is much

better than on pre-calculated meshes. The

disadvantage is that they require a lot more

processing than pre-calculated meshes do. To make

up for this a simple parallelization mechanism is

shown in this paper.

2.2 Mesh Representation

Multiresolution representations based on right-

triangle triangulations are the most suitable for

adaptive terrain modelling of regular height field

data, where a multi-resolution surface is stored in a

data structure that can be recursively refined on

demand. Among these we can mention the quatree

and bintree methods (Lario, Pajarola and Tirado,

2003). Quad-Trees have the disadvantage though,

that they are inherently based on recursive quads

which can have up to four children. For our purpose

a structure that is inherently based on triangles is

much better suited given the refinement technique

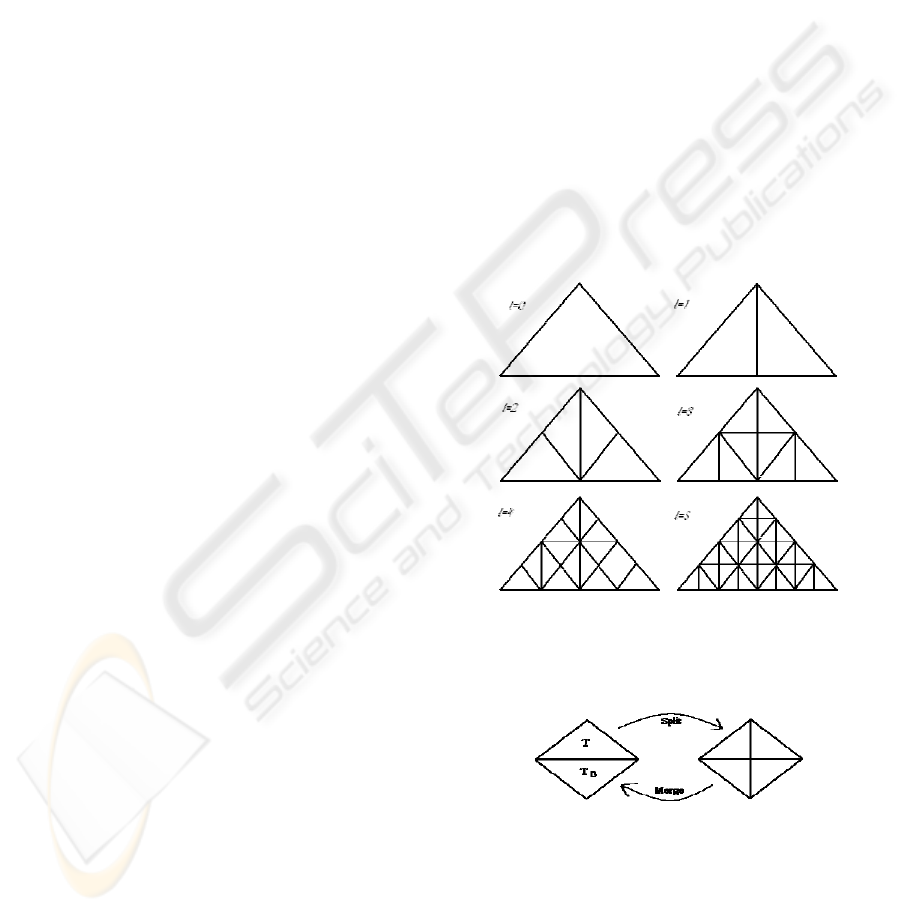
described later. In a Binary Triangle Tree, each of

two possible children are triangles formed by

dividing the parent triangle in two by longest edge

bisection as illustrated in Figure 1. For a discussion

and evaluation of the bintree multiresolution

representation see (Duchaineau et al, 1997; Pajarola

2002).

Figure 1: First 6 levels of a Binary Triangle Tree.

Figure 2: Split and Merge operations.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

334

3 NON-PARALLEL BINTREE

PATH-BASED METHOD

The serial method chosen to represent terrain is a

simple version of ROAM. The algorithm can be

described as follows:

Serial Tessellation Algorithm:

Input: A high resolution height map terrain data.

a) The terrain data is divided into N square patches.

b) Each terrain patch is initialized with two bintree

triangle structures at the coarsest level (every patch

contains two triangles). The height coordinate of

each triangle vertex is given by the corresponding

value in the height map.

c) All triangles are linked together by pointers to

their three neighbours.

For each frame adaptively do:

d) The landscape is initialized and the adaptive

view dependant level of detail tessellation process

is performed.

e) The frame is rendered.

For ends.

The terrain is subdivided into bintree patches in

order to keep the depth of the tree structures

controlled.

During the tessellation process (Duchaineau et

al, 1997) the mesh is dynamically calculated for

each frame. This is done by recursively traversing

the two BTT structures in each visible patch and

refining it until the desired level of detail is reached.

This is done with two basic mesh operations called

merge and split (see figure 2).

When two adjacent triangles are both from the

same level we refer to it as a diamond. Split replaces

a triangle T with its children T0 and T1 and does so

with the adjacent triangle as well. This introduces a

new vertex at the centre of the diamond, resulting in

a new continuous triangulation.

This tessellation process is by far the most CPU

expensive part of the algorithm. During this process,

each visible patch is visited and their BTT structures

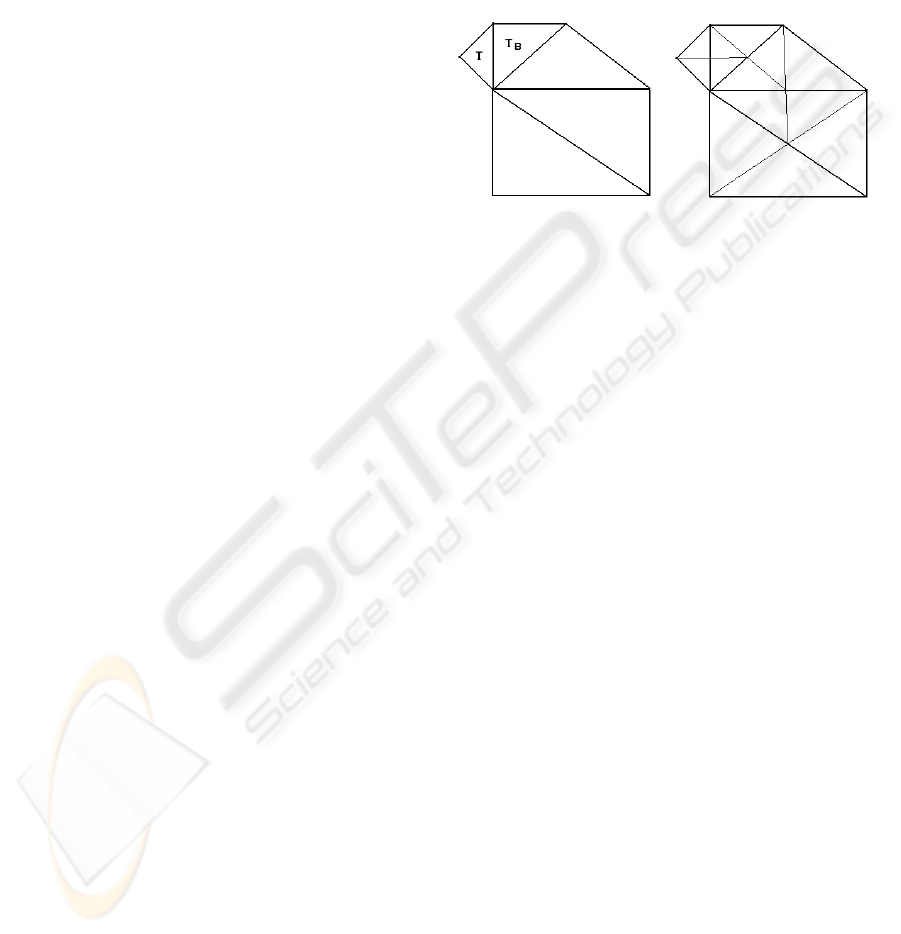
recursively traversed and refined. A triangle T in a

triangulation cannot be split immediately when its

base neighbour Tb is of a coarser level. It would

produce a crack in the mesh, so we have to force T

to split. To force T to split, Tb must be forced to

split first, which may require other triangles to split

first. As long as we recursively split all required

triangles, the mesh will remain consistent. This is

also known as the Longest Edge Propagation Path or

LEPP (Rivara, 1997), which finishes finding a

terminal edge, which is the base edge for two

adjacent triangles or an edge of the border of the

mesh. Only then we start the splitting process (see

figure 3).

If we go on refining too much, we can eventually

run out of memory. To avoid this, a pool of possible

vertices to be allocated is defined. Once a new

vertex is introduced, it is eliminated from the pool

and becomes part of the triangulation. Once we run

out of vertices in pool, no further refinement is

possible.

Figure 3: In order to split T all the triangles along the

longest edge path have to be split first.

Since we want different levels of refinement on

different areas of the mesh, we need to decide how

far to refine the mesh in a given point. This is done

by introducing an adaptive tolerance parameter t

which depends on the distance of the given point to

the observer.

Each time that a triangle in the BTT is analyzed

we compute t for the given position and compare its

value with the distance between the middle point of

the triangles base and the corresponding point in the

Height Map. If the distance is bigger than our

calculated t we split the triangle. In this way we

achieve our goal of continuous level of detail.

4 PARALLEL TESSELLATION

With multiple processor technology the tessellation

could be done in a fraction the time if the meshing

problem is decoupled. The problem that arises is that

given the recursive nature of the process, the CPUs

might want to allocate the same vertex at the same

time, causing access violations and ending the

process. The first approach to solve this problem is

to work on separate meshes and thereby distributing

the process completely. This causes a problem of

continuity at the bounding of adjacent meshes. For

illustration purposes, let us focus on dual processor

scenario. As both meshes are refined independently,

we have no guarantee the union is going to be

continuous and therefore cracks may appear at the

union.

UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE

TRIANGULATIONS

335

Other algorithms solve the problem by

concurrent vertex insertion (Chernikov and

Chrisochoides, 2004), scheduling the point insertion

in such a way that no access violations will occur

during the refinement. The problem could be solved

by using a different mesh structure but we want to

keep the efficiency of the BTT structure. The

solution implemented in this paper works by

decoupling the mesh, and working on it as if it were

two separate meshes, but maintaining consistency.

This way we do transform the process into a

distributed problem but with shared memory

resources.

The solution implemented parallel tessellation

algorithm works as follows:

Input: a high resolution height map terrain data.

The terrain data is divided in N square patches.

Each terrain patch is initialized with two bintree

triangle structures.

While the observer traverses the terrain do

For each frame (observer position) do

- the mesh is partitioned along the observer line L

and common parameters t are calculated along L.

- each submesh and associated parameters t are

assigned to each processor for tessellation.

- each submesh is adaptively calculated in parallel

using bintree triangle structures until the desired

level of detail is achieved.

For ends.

While ends.

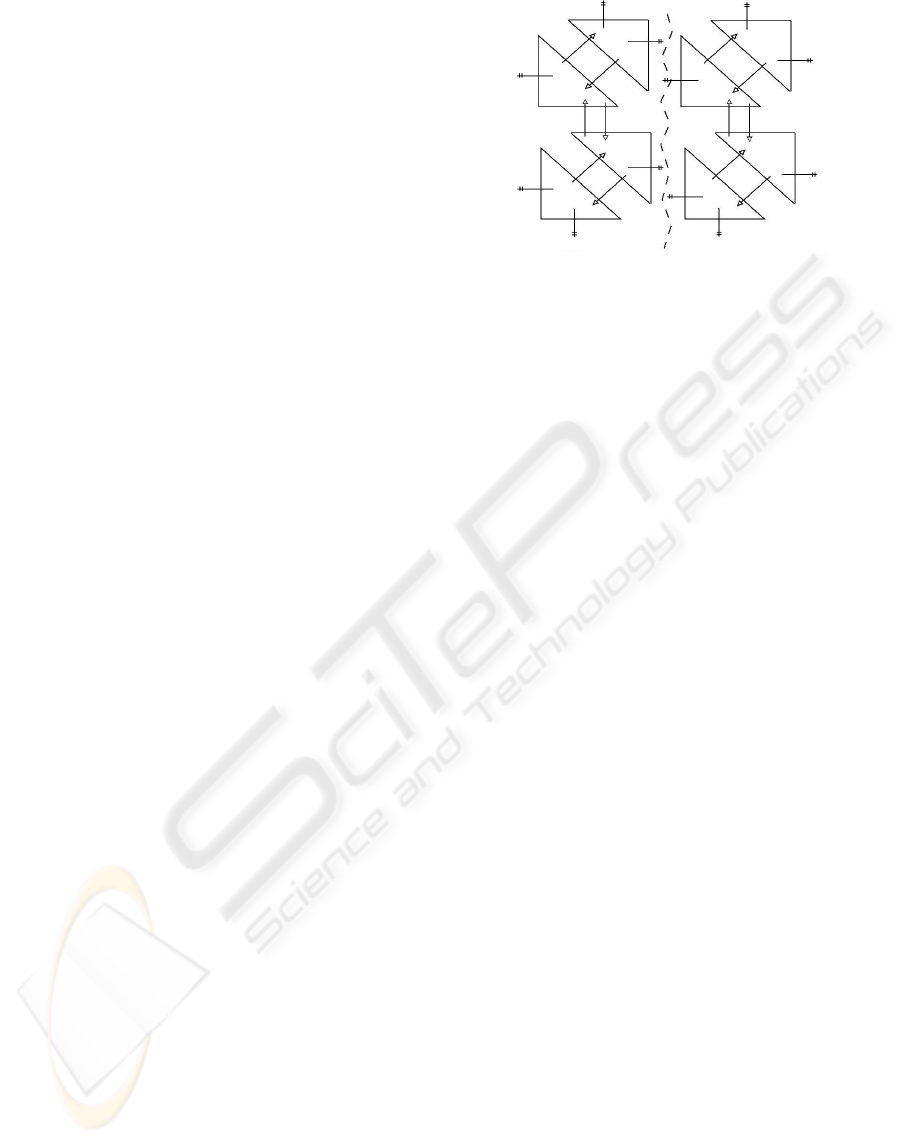
The reason to partition the mesh along the line of

observation is to balance processor load. This can be

easily done by identifying the patches at each side of

the observer and accessing their BTT structures.

At the initialization stage all triangles of the BTT

structures would be linked together in the serial

algorithm, instead each half of the mesh is linked

together, leaving an unconnected division of it

running through the middle of the mesh (see figure

4). This way we assure that it is a decoupled

problem because the edges in the middle of the mesh

become terminal edges, were the refinement stops.

More on decoupled parallel refinement can be found

in (Rivara et al, 2006).

After splitting the mesh two separate pools for

vertex allocation are defined. This way both halves

can be refined independently without sharing

resources.

The LOD is computed by two tessellation

threads. These can be assigned to separate CPUs.

The tessellation process is the same as in the non-

parallel case using the method described above.

Each of the tessellation threads has its own pool

of vertices and set of patches containing the BTT

structures, the only shared resource is the height

map. If we would duplicate the height map and

include a copy of the height map to each thread, the

process would be completely distributed and

therefore have no shared memory resources. This

could be useful to run the algorithm on a cluster of

machines.

For the parallel processor problem, the access to

the height map does not present any problems,

because each thread is dealing with a different part

of the terrain and therefore there is no possibility

that both threads would try to access the same value.

Once the tessellation process is complete, and

before the rendering step can start, the two halves

have to be consistent with each other to avoid cracks

at the initial division line of the mesh. At this point

we have no guarantee that both parts of the meshes

fit together without leaving cracks at the union. To

ensure consistency we force the tolerance factor t at

both adjacent borders to be exactly the same. This

means the same level of detail will be used on both

halves and the condition to stop refining is the same

at both sides of the union as long as we had enough

vertices in the pool. This produces a mesh with

duplicate vertex at the union and thus producing a

few extra triangles, but with no cracks in the mesh.

We are also over-refining the neighbouring mesh.

This causes a few extra triangles to appear at the

coarser side of the mesh. The triangle overhead is a

small price to pay, given the fact we have done the

tessellation in almost half the time.

5 RESULTS

To test the performance of the algorithm, a parallel

version and a non-parallel version of the same

algorithm were implemented and compared in terms

of CPU load, memory usage and frames per second

performance.

The testing method used can be described as

follows. A 230 second long flight over the terrain

Figure 4: The initial mesh is divided. The triangles

running along the middle are uncoupled.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

336

was programmed and executed ten times. Each of

the flights was done rendering the scene at different

levels of detail, starting with 180000 vertices and

ending at 5000. Each flight was performed with the

serial and the parallel algorithm and CPU load and

frames per second were measured for both

algorithms. The number of desired vertices per

frame, maximum allowed time and circuit were

given. Spatial steps were calculated in terms of the

elapsed time, total time allowed and position. The

test platform was a dual Turion64 processor

computer, running at 1.6 GHz with 1 GB of RAM

and an Nvidia GeForce 6100 graphics card running

Windows XP.

The results are illustrated in the following table:

Table 1: Performance of sequential and parallel algorithm.

Vertices

per

Frame

Average

Sequential

frames/sec

Average

Parallel

frames/sec

% Increase

Performance

180000 17.03 23.78 39.64

160000 17.42 25.31 45.29

140000 20.22 33.10 63.70

120000 21.05 35.71 69.64

100000 23.61 39.85 68.78

80000 28.60 44.57 55.84

60000 39.42 57.35 45.48

40000 52.19 68.16 30.60

20000 71.04 73.06 2.84

5000 81.03 81.18 0.19

The same experiment executed over different

terrain data yielded similar results.

As shown in figures 6 to 8, the average CPU

load was well balanced. The load balance was not

exactly the same due to differences on the terrain

geography on each side of the mesh division.

Although one might be tempted to think that the

performance should increase by a bigger factor, we

need to have in mind the fact that all we have done

is parallelizing the tessellation process, but other

processes like computing texture coordinates are

done sequentially. Given this, the increase in frames

per second performance shown in table 1 is

considerable. As shown in table 1, the increase in

performance was at its maximum between 100 000

and 160 000 vertices per frame. When decreasing

the amount of vertices, the parallel algorithm shows

smaller improvement over the sequential algorithm.

This happens because at low workloads one CPU is

able to manage all of the work, improvement starts

to be noticeable at 40 000 vertices. On the other end,

with over 160 000 vertices the improvement of the

parallel algorithm over the sequential one starts

decreasing until it stays at around 39 %.

The memory usage showed no considerable

change between the serial and the parallel algorithm.

In both algorithms the entire structure could be

stored in the same amount of memory. This was to

be expected as the mesh size did not change and no

extra storage space was needed. The structure took

about 1.2 MB of storage space at low vertex rates.

This increased to a maximum of 17.2 MB at 180 000

vertices per frame.

Figure 6: CPU load at 180 000 vertices per frame.

Figure 7: CPU load at 100 000 vertices per frame.

Figure 8: CPU load at 20 000 vertices per frame.

Figure 5: Terrain mesh.

UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE

TRIANGULATIONS

337

6 CONCLUSIONS AND

DISCUSSION

We have presented a parallel continuous level of

detail technique for rendering bintree based

structures. The mayor improvements in performance

are achieved by turning the problem into an

uncoupled refinement process, which allows a

terrain mesh to be generated on multiple processors

and thereby increasing the performance in terms of

frames per second considerably.

The issue of keeping the load balanced on more

than two processors posts some difficulty because

the mesh partitioning strategy needs to be

generalized. Due to the decreasing level of detail

towards the observers horizon, and the changes in

complexity of the mesh, the next partition strategy is

much harder to determine and will be part of future

research.

This paper focused on showing the increase in

performance by parallel mesh tessellation, but many

improvements can still be implemented, like node

caching, triangle fan generation, priority queues and

occlusion culling among other techniques.

ACKNOWLEDGEMENTS

This work was partially funded by Fondecyt

1040713. We are also grateful to the referees whose

comments contributed to improve this paper.

REFERENCES

Mark Duchaineau, MurrayWolinsky, David E. Sigeti,

Mark C. Miller, Charles Aldrich, Mark B. Mineev-

Weinstein, ROAMing Terrain: Real-time Optimally

Adapting Meshes In Roni Yagel and Hans Hagen,

editors, IEEE Visualization '97, pages 81--88. IEEE

Computer Society Press, Los Alamitos, CA,

November 1997.

Willem H. de Boer, Fast Terrain Rendering Using

Geometrical MipMapping E-mersion Project,

http://www.connectii.net/emersion, October 2000

E. J. Padrón, M. Amor, M. Bóo, R. Doallo, Efficient

Parallel Implementations for Surface Subdivision. In

Fourth Eurographics Workshop on Parallel Graphics

and Visualization, Pages: 113 - 121 (2002)

Andrey N. Chernikov, Nikos P. Chrisochoides, Practical

and Efficient Point Insertion Scheduling Method for

Parallel Guaranteed Quality Delaunay Refinement. In

Proceedings of the 18th annual international

conference on Supercomputing, Pages 48-57 2004

Martin Bokeloh, Michael Wand, Hardware Accelerated

Multi-Resolution Geometry Synthesis. In Proceedings

of the 2006 symposium on Interactive 3D graphics and

games, Pages 191-198

Joshua Levenberg, Fast view-dependent level-of-detail

rendering using cached geometry. In Proceedings of

the conference on Visualization 2002, Pages 259-266

María Cecilia Rivara, Using Longest-Side Bisection

Techniques for Automatic Refinement of Delaunay

Triangulations. In International Journal for Numerical

Methods in Engineering 1997, Pages 581-507

Renato Pajarola, Overview of Quadtree-based Terrain

Triangulation and Visualization. In Technical Report

UCHCS-02-01, Information and Computer Science,

University of California, Irvine, 16 pages, 2002

M.C. Rivara, C. Calderon, A. Fedorov, N. Chrisochoides,

Parallel Decoupled Terminal-Edge Bisection Method

for 3D Mesh Generation. In Engineering with

Computers, 22(2): Pages 111-119, 2006

Hugues Hoppe. Smooth view-dependent level-ofdetail

control and its application to terrain rendering. In

Proceedings Visualization 98, pages 35–42. IEEE,

Computer Society Press, Los Alamitos, California,

1998.

H. Hoppe. Progressive meshes. In Proceedings

SIGGRAPH 96, pages 99–108. ACM SIGGRAPH,

1996.

Michael Garland and Paul S. Heckbert. Fast polygonal

approximation of terrains and heigt fields. Technical

Report cmu-cs-95-181, School of Computer Science,

Carnegie Mellon University, Pittsburgh, PA, 1995.

Mathias Holst and Heidrun Schumann. Efficient

Rendering of High –Detailed Objects Using a Reduced

Multi-Resolution Hierarchy. In Proceedings of

GRAPP 2006, Pages 3-10.

Leila De Floriani, Paola Magillo, and Enrico Puppo.

Building and traversing a surface at variable

resolution. In proceedings of the 8

conference on

visualization 1997, pages 133-ff. IEEE Computer

Society Press.

Peter Lindstrom and Valerio Pascucci. Visualization of

Large Terrains Made Easy. In Proceedings of the

conference on Visualization 2001,Pages 363-371.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

338