
HYBRID RAY TRACING
Ray Tracing Using GPU-Accelerated Image-Space Methods
Philippe C. D. Robert, Severin Schoepke and Hanspeter Bieri
Institute of Computer Science and Applied Mathematics, University of Bern
Neubr
¨
uckstrasse 10, 3012 Bern, Switzerland
Keywords:
Hybrid Ray Tracing, Object Intersection Buffer, Image-Space Rendering Techniques.
Abstract:
In recent years, interactive ray tracing has become a reality, although mainly by using clustered workstations
and sophisticated acceleration structures. On non-clustered computer architectures this is still not an easy
task, especially when rendering animated scenes, even though the computation power of modern worksta-
tions is increasing rapidly. In this paper we propose known image-space rendering techniques to be used
for accelerating ray tracing. Firstly, we describe a GPU-based visibility preprocessing algorithm to perform
interactive ray casting by applying the standard depth testing capability of graphics processing units. This
method – called object intersection buffer (OIB) – is particularly suitable for ray casting animated scenes, as it
completely avoids the necessity of creating and updating any kind of spatial acceleration structures in order to
achieve high frame rates. Then we integrate shadow rendering into our ray caster using the shadow mapping
technique to avoid computationally expensive shadow rays. Then, we convert our GPU-based ray caster into
a hybrid ray tracer by computing reflection and refraction rays on the CPU using a spatial acceleration struc-
ture. This allows us to exploit parallel rendering to increase the overall frame rate. Finally, we compare our
implementations to each other and analyse their advantages and disadvantages in terms of visual quality and
rendering performance.
1 INTRODUCTION
Image-space rendering techniques have been used to
accelerate ray tracing since the late 1980s. At that
time graphics hardware was not yet as powerful as
today, so there was no advantage in using hardware
accelerated methods to speed up ray tracing. In the
last few years this has changed substantially and our
paper intends to exploit some of these new possibili-
ties. We propose the object intersection buffer (OIB)
technique as a means to accelerate the first hit compu-
tations based on common screen-space visibility pro-
cessing methods using capabilities of programmable
graphics processing units (GPU) .
In a first application we utilise the OIB to perform
interactive ray casting, thereby eliminating the neces-
sity of creating and updating any kind of spatial accel-
eration structures in order to achieve high frame rates.
This is particularly useful for rendering animated or
dynamic scenes. We then compare this approach with
an implementation which is based on traditional ray-
object intersection testing. In addition, we describe
ways to further speed up the rendering performance
using interleaved sampling and colour interpolation
techniques. Moreover, we integrate shadow rendering
into our ray caster and avoid common shadow feel-
ers by using the shadow mapping technique, instead.
As it has become feasible to perform general-purpose
computations on programmable graphics hardware,
we also describe an implementation of our ray caster
that runs completely on the GPU. This makes it possi-
ble to use the processing power of the host computer
for other purposes, such as advanced shading or non-
rendering related tasks. In a second application we
apply the OIB to increase the performance of stan-
dard ray tracing using a hybrid rendering pipeline.
Whereas we compute the primary rays on the GPU
using an OIB we compute secondary rays on the host
processor. Even though this requires a spatial accel-
eration structure we are able to increase the render-
ing performance by sharing the load between the CPU
and the GPU using a parallel execution mode.
1.1 Related Work
The idea of using screen-space coherence to acceler-
ate ray tracing came up in the late 1980s. Weghorst,
Hooper and Greenberg introduced a method based on
305
C. D. Robert P., Schoepke S. and Bieri H. (2007).
HYBRID RAY TRACING - Ray Tracing Using GPU-Accelerated Image-Space Methods.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 305-311
DOI: 10.5220/0002081603050311
Copyright
c
SciTePress
item buffers to reduce the total number of intersection
tests for primary rays (Weghorst et al., 1984). Item
buffers simply store the indices which reference those
objects within the scene which are visible at the given
location in the image plane. As a consequence, a triv-
ial lookup operation can be used to determine the vis-
ible object for a specific pixel, hence no acceleration
structure is needed to produce high frame rates. This
approach is the basis of many contributions, including
ours (Salesin and Stolfi, 1989; Lamparter et al., 1990;
Kim et al., 2000).
With the advent of programmable graphics hard-
ware it has become feasible to offload arbitrary com-
putational tasks to the GPU using a stream processing
model (Bolz et al., 2003; Buck et al., 2004; Fatahalian
et al., 2004; Owens et al., 2005; Lefohn et al., 2006).
In (Carr et al., 2002) the authors were able to im-
plement a fixed-point ray-triangle intersection testing
engine on an ATI R200. Around the same time Pur-
cell et al. (Purcell et al., 2002) developed a complete
ray tracing pipeline on a GPU simulator. Since then
others have implemented classical ray tracers on the
GPU using the extended feature set of modern GPUs
(Karlsson and Ljungstedt, 2004; Christen, 2005). In
(Weiskopf et al., 2004) a non-linear ray tracer on the
GPU is implemented using several acceleration tech-
niques, such as early ray termination and adaptive ray
integration. In (Simonsen and Thrane, 2005) vari-
ous ray tracing acceleration structures on the GPU are
compared, whereas in (Foley and Sugerman, 2005)
the kd-tree acceleration structure is used to perform
ray tracing on the GPU. In (Carr et al., 2006) a method
for quick intersection of dynamic triangular meshes
on the GPU is introduced, based on a threaded bound-
ing volume hierarchy built from a geometry image.
The method we propose in this paper builds on this
previous work by combining and extending a number
of techniques in a novel way to increase the rendering
performance of ray tracers.
2 RENDERING ALGORITHMS
In the following sections we will outline the OIB
method and – shortly – the shadow mapping tech-
nique. For the sake of simplicity and rendering perfor-
mance we thereby concentrate on rendering triangles.
2.1 Object Intersection Buffer
One of the biggest challenges when performing inter-
active ray tracing is how to reduce the total number of
ray-object intersection tests to a minimum (Reshetov
et al., 2005). Usually this is done by dividing the 3D
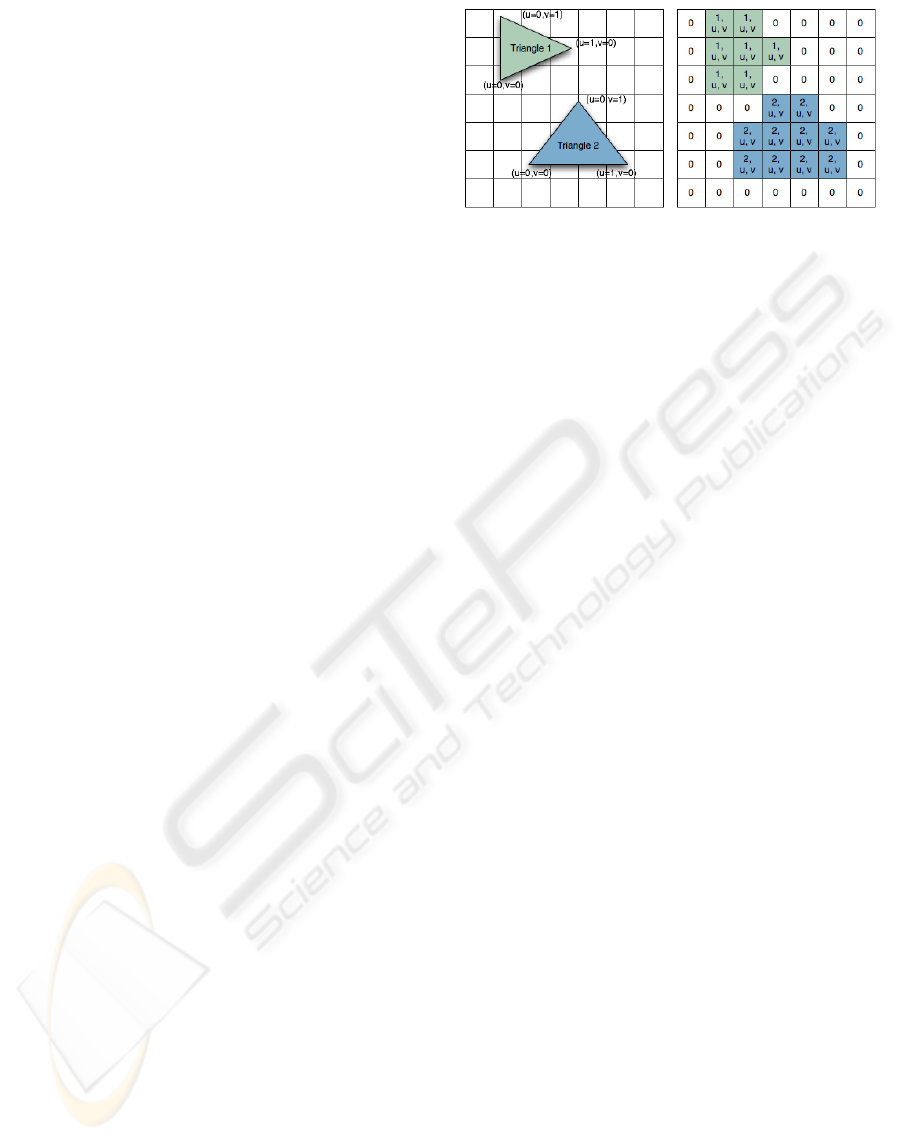
Figure 1: The OIB data structure contains the object indices
(right) as well as the interpolated (u, v)-coordinates of the
visible triangles (left).
space into subsets, each containing a certain number
of objects. For this purpose some kind of acceleration
structure is used – e.g., kd-trees, grids or bounding
volumes. Fast traversal routines can then be applied
to decide which subsets of the scene to pick in order to
compute the proper ray-object intersection. Unfortu-
nately, creating and updating acceleration structures is
time- and memory-consuming, especially when ren-
dering dynamic scenes. We propose a method to com-
pute the first hits using an object intersection buffer
(OIB), based on hardware-accelerated triangle raster-
isation. For each pixel the OIB stores a reference to
the triangle which is visible at that position as well
as the (u, v)-coordinates of the hit point, which are
given for each vertex and interpolated for the rest of
the triangle; this is outlined in Figure 1. We describe
two algorithms to build the OIB. The first is a direct
extension of the item buffer method, the second is bet-
ter adapted for GPU acceleration. Our first algorithm
works as follows:
1. The index of every triangle is encoded into a RGB
colour value. In this way it is possible to address
up to 2
24
triangles.
2. Every triangle of the scene is rendered using
OpenGL; its index is thereby passed to the GPU
as a vertex colour. During this process we perform
hidden surface removal.
3. For every pixel the visible triangle is determined
by a triangle lookup operation using the properly
decoded triangle index from the framebuffer.
4. For each visible triangle exactly one ray-triangle
intersection test is performed and the result is
stored in the OIB.
Based on the information stored in the OIB we
can now perform the shading operations or compute
secondary rays. In either case the final performance
heavily depends on efficient and reliable visibility
processing. Commonly this is done using the z-buffer
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
306
hidden-surface algorithm (Sutherland et al., 1974).
We use the hardware accelerated OpenGL depth test-
ing which guarantees a high rendering performance.
Please note that since this is a screen-space based
method, it is even possible to scale the creation of
the OIB using distributed sort-first parallel rendering
(Molnar et al., 1994) by applying multiple GPUs.
To further increase the OIB creation performance
we propose a second algorithm based on (u, v)-
mapping (Heckbert, 1986), called direct rendering.
Instead of performing ray-triangle intersection tests
we use a GPU-based (u, v)-mapping to determine the
first hits. Moreover, rather than passing the triangle
indices as vertex colours we use texture coordinates –
thus, we avoid the encoding and decoding stages al-
together. A vertex shader then stores the indices as
well as the (u, v)-coordinates in gl TexCoord, which
for every fragment of the triangle gets written to the
target buffer by the subsequent fragment shader.
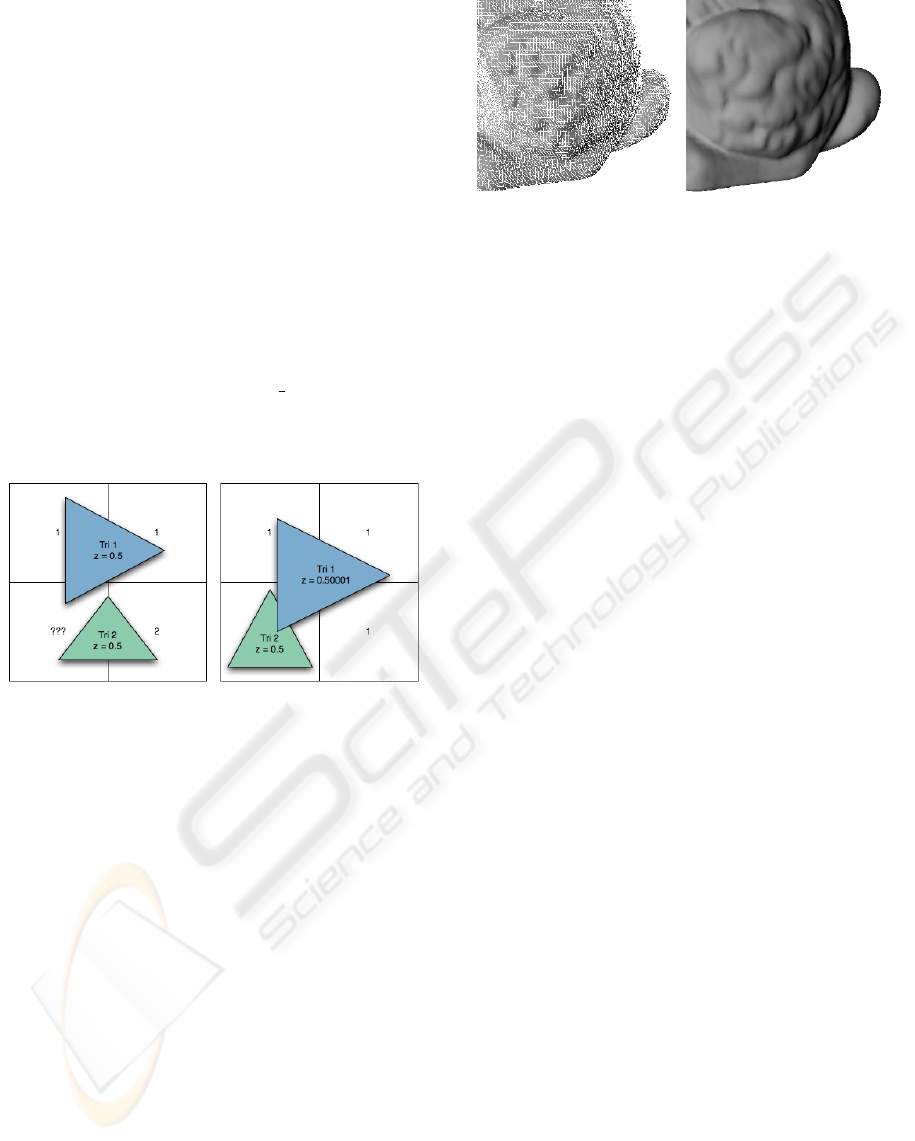
Figure 2: Two triangles with the same z-value z = 0.5 (left)
and two overlapping triangles with almost the same z-value
where the depth test fails (right).
When calculating the ray-triangle intersections as
opposed to using the (u, v)-mapping, the GPU’s depth
buffer reveals a bothering constraint. On current
graphics hardware the depth buffer is scaled loga-
rithmically and limited to 24 bit precision. Under
some circumstances this can cause artefacts because
of failing ray-triangle intersection tests. This happens
whenever the OIB contains references to ”wrong” tri-
angles due to wrong depth test results. This is shown
on the right of Figure 2. A similar problem may ap-
pear at the borders of neighboured triangles where the
index of a wrong triangle may be written to the OIB
due to the limited resolution of the framebuffer – this
is depicted on the left of Figure 2. Unfortunately both
problems can appear simultaneously. We try to over-
come these shortcomings by applying multisampling
as described in Section 3 in order to determine the
correct intersections for all primary rays. The results
are visually appealing; a typical example is given in
Figure 3.
Figure 3: Artefacts without multisampling and interpolation
(left), and no visible artefacts with 3 × 3 multisampling and
interpolation (right) [part of the Stanford bunny].
2.2 Shadow Mapping
Because it is not feasible to compute shadow rays ef-
ficiently by only using an OIB, we perform shadow
rendering using the image-based shadow mapping
technique (Williams, 1978) which also depends on
the depth buffer hidden-surface algorithm. Shadow
mapping is thus fully accelerated on the GPU. The
most important aspect of this technique is that the
depth buffer generated by rendering the scene from
the light’s point of view is the same as a visibility test
over the light source’s viewing volume. It can thus
be used directly as a shadow map which partitions the
view in both illuminated and shadowed regions.
The algorithm itself is simple: First, the scene is
rendered from the light’s point of view. Consequently,
the z-values for the objects closest to the light source
are stored in the depth buffer resulting in the shadow
map. Then the scene is rendered from the camera’s
point of view, and as each fragment is generated it is
transformed into the light sources coordinate system
and tested for visibility. If the distance to the fragment
is greater than the value stored in the shadow map,
there is some object in front of it and thus it lies in
the shadow. Otherwise it is illuminated. Please note
that the shadow map only needs to be updated when
the scene is subject to changes while rendering – e.g.,
moving light sources or altering the geometry.
3 IMPLEMENTATION
In this section we outline different approaches to im-
plement the OIB. Please note that we do focus solely
on the OIB itself, other aspects of the implementa-
tion are kept at a basic level. We do not use any
SIMD functionality of modern CPUs to exploit ray
coherence, and we use the simple Phong illumination
model, for example. Advanced shading and texturing
models can be integrated easily, though.
HYBRID RAY TRACING - Ray Tracing Using GPU-Accelerated Image-Space Methods
307

3.1 Ray Casting on the CPU
Integrating the OIB based visibility processing and
shadow mapping into a ray caster leads to the fol-
lowing multi-pass rendering algorithm: At first, we
create an OIB which holds the indices and of all
currently visible triangles including the correspond-
ing first hit coordinates. For this purpose we use a
32bit floating point off-screen framebuffer object
(FBO) with a depth attachment. Then for every light
source we create a shadow map by rendering the en-
tire scene from the light’s point of view. Again we use
an FBO to accomplish this task. Finally the OIB and
the shadow maps can be transferred from the GPU
to host memory to perform the shading. To hide the
delay caused by this operation we perform an asyn-
chronous memory transfer using the OpenGL pixel
buffer object extension (PBO). This allows us to
begin with the shading or intersection testing before
the entire OIB is downloaded completely.
If we do not use (u, v)-mapping to detect the first
hit points we have to perform standard ray-triangle
intersection testing. Our ray-triangle intersector code
is based on the algorithm introduced in (M
¨
oller and
Trumbore, 1997). For every primary ray we perform
one ray-triangle intersection test, the correct triangle
is thereby quickly determined using a trivial lookup
operation based on the index stored in the OIB. If
there is an intersection we shade the pixel accord-
ing to the shadow map and lighting model, if the test
fails we perform additional intersection tests to avoid
rendering artefacts. This is done using the following
”lazy multisampling” strategy: if the first intersection
test fails we loop over the local n × n neighbourhood
in the OIB and perform n
2
− 1 ray-triangle intersec-
tion tests with the triangles referenced by the indices
of the surrounding buffer entries. In most cases we
are able to find correct intersections. If not, we inter-
polate the pixel colour using the surrounding pixels.
Using this multisampling strategy the OIB has exactly
the same dimensions as the framebuffer.
To further accelerate the rendering we imple-
mented interleaved rendering. In this mode we only
shoot every nth primary ray, the remaining pixels are
then coloured using interpolation in a second render-
ing pass. Because this technique leads to higher frame
rates than normal rendering but also to a blurred im-
age, it is especially useful when visualising camera
animations. In Figure 4 we compare interleaved and
normal rendering. Another approach to avoid the arte-
facts mentioned before would be to supersample the
entire scene. The obvious drawback of this method is
that many more primary rays have to be computed in
order to produce the final image.
Figure 4: Interleaved rendering (left) leads to higher frame
rates than normal rendering (right), but also to a blurred im-
age (part of the BART robots scene (Lext et al., 2000)).
3.2 Ray Casting on the GPU
To achieve a higher rendering performance we
rewrote our ray caster to run completely on the GPU
using a fragment shader program. Among other im-
provements this allows us to get rid of the OIB and
shadow map readback operations. On the other hand,
to access the scene data on the GPU – such as ver-
tices, normals, colours, etc. – we have to transfer it
to the GPU using multiple 32bit floating-point RGBA
textures. Still, we do not only profit from the superior
performance and parallelism of modern GPUs but we
may also use the free CPU cycles for other purposes;
e.g., advanced shading and texturing.
The first step of the GPU-based ray caster – OIB
creation – is done similarly to that of the CPU based
version. But instead of reading the data back to host
memory it remains on the GPU as a texture. The same
holds for the shadow maps. We then activate our ray
caster fragment shader and draw a screen-sized quad
enforcing one fragment shader pass per pixel. For
every pixel the shader reads the index from the OIB
texture and performs the intersection test or uses the
interpolated (u, v)-coordinates to determine the inter-
section point on the referenced triangle. If a hit has
been detected the pixel is shaded appropriately.
3.3 Hybrid Ray Tracing
While ray casting based on the OIB leads to high
frame rates, the visual quality is less stunning. To
improve this we add support for reflections and re-
fraction by shooting secondary rays (Figure 5).
We do this by first rendering the primary rays for
frame n on the GPU using an OIB as described in
3.2 and then transfer the results to the host computer
where the additional rays are traced using a kd-tree
acceleration structure; meanwhile the GPU processes
the primary rays for the next frame n+1. This parallel
execution introduces one frame of latency but ideally
also hides the OIB memory transfer from the GPU to
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
308

Figure 5: The animated robots scene rendered with reflec-
tions by our hybrid ray tracer.
the host memory.
In order to optimise the rendering performances
we implemented a surface area heuristic (SAH) for
creating the kd-tree, closely related to that of (Wald
and Havran, 2006). This approach leads to faster
tree traversals but also introduces considerable pre-
processing costs and is thus more or less inappropri-
ate for rendering dynamic scenes. It would be feasi-
ble though to improve this using an implementation
solely based on the GPU. The host processor could
then be used for updating the acceleration structure.
4 DISCUSSION AND RESULTS
We benchmarked our implementations on an AMD
Athlon64 3500+ / GeForce 7800GT workstation run-
ning Windows XP. Tests on a dual 2.8 GHz Xeon CPU
workstation running Fedora Core 5 Linux led to com-
parable results. For the benchmarks we used three
different scenes of various complexity, i.e. a simple
torus, the well-known Stanford bunny and the hier-
archically animated robots scene from the BART ray
tracing benchmark (Lext et al., 2000); see Table 1.
One light source is enabled while rendering, screen
resolution is always 800 by 600 pixels.
Table 1: The sample scenes and their number of triangles.
Name Triangles Notes
Torus 1024 A simple scene
Bunny 69451 The Stanford bunny
Robots 71708 An animated scene
Since the base number of primary rays is the same
for all three scenes we expected other factors to be
significant with respect to frame rate differences; e.g.,
the OIB and shadow map creation costs, OIB multi-
sampling or dynamic scene updates. In order to ac-
cess the OIB on the CPU we have to perform a frame-
buffer readback operation. Now, unlike in the past,
due to the high bandwidth of the new PCI Express
for Graphics (PEG) standard this does not lead to
a dramatic performance penalty anymore, especially
when using asynchronous memory transfers. Along
the same lines, OIB creation takes between 3ms and
15ms depending on the scene. This could be further
optimised using advanced OpenGL rendering tech-
niques instead of the immediate mode rendering, as
it is the case with our code.
4.1 Ray Casting
The OIB based ray caster seems to perform reason-
ably well compared to a traditional implementation
based on a kd-tree – see Table 2 for the results. When
comparing the frame rates of the CPU and GPU based
implementations it becomes obvious that the latter is
faster almost by an order of magnitude. This can be
explained by the fact that we profit from the paral-
lelism on the GPU whereas we did not use multiple
threads to perform the ray shooting or shading on the
host. In addition, we did not have to perform memory
transfers between the GPU and the host memory, only
the dynamic robots scene is slowed down by frequent
data texture updates.
Table 2: Rendering performances (fps) measured with and
without shadow rendering (without multisampling).
Torus Bunny Robots
CPU (kd-tree) 1.7 1.3 0.2
CPU 8.0 8.5 3.0
CPU, shadows 6.9 7.5 1.4
GPU 112 36 18
GPU, shadows 105 35 2.4
GPU, direct 165 47 18
GPU, direct, shadows 129 46 2.4
Not surprisingly, direct rendering using (u, v)-
mapping leads to higher frame rates than calculat-
ing the intersection points. The achieved speedup for
static scenes is in the range of 25 to 50 percentage.
Again though, in case of the dynamic robots scene,
this advantage is virtually negligible as recomputing
the shadow map every frame has a much higher im-
pact on the total performance. The reason for the
relatively high frame rates of the bunny is that the
model fills the viewport to a lesser extent than the
other scenes and thus less intersections occur, leading
to fewer shading operations.
It is obvious that when performing OIB multi-
sampling, the rendering performance drops notice-
HYBRID RAY TRACING - Ray Tracing Using GPU-Accelerated Image-Space Methods
309
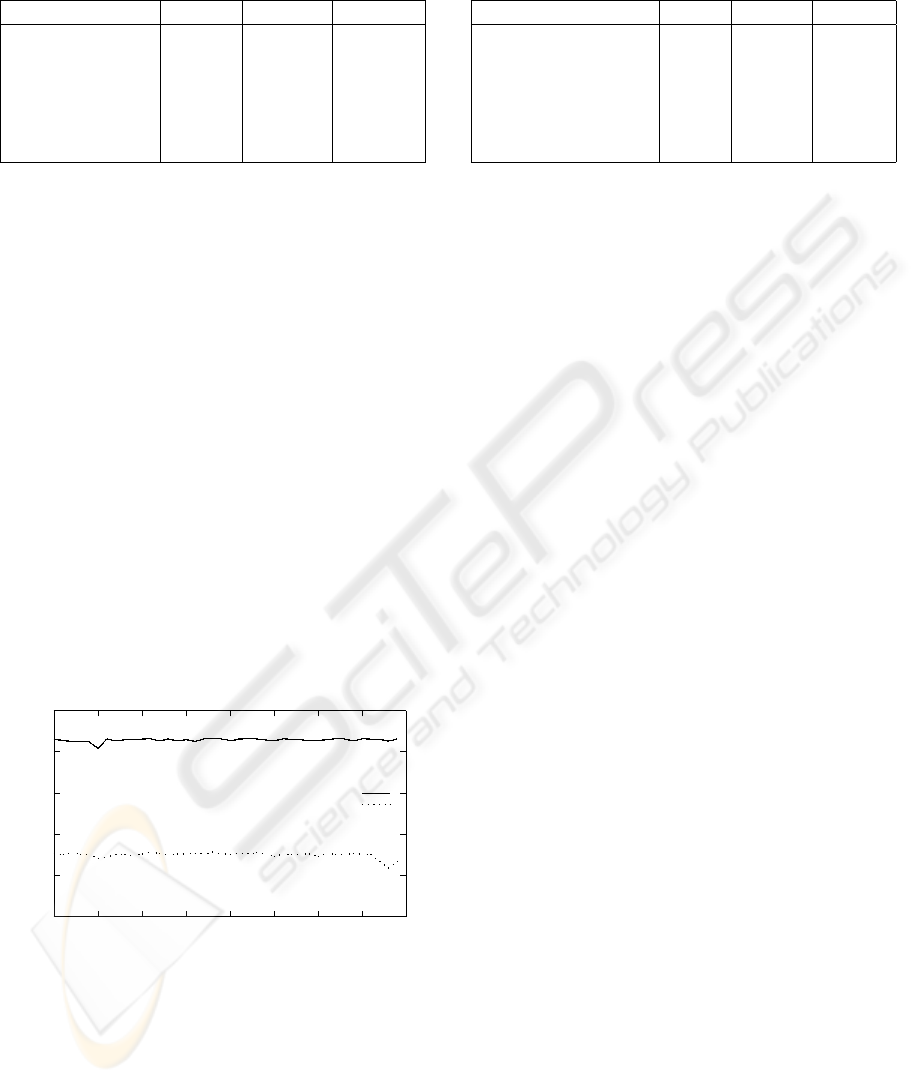
Table 3: Rendering performances (fps) measured with and
without (lazy) multisampling (without shadow mapping).
Torus Bunny Robots
CPU 8.0 8.5 3.0
CPU, interleaved 10.2 10.0 4.3
CPU, lazy 3 × 3 7.6 5.5 2.9
CPU, lazy 5 × 5 7.5 4.3 2.8
CPU, 3 × 3 4.8 3.7 2.3
CPU, 5 × 5 3.3 2.2 1.9
ably. In most cases ”lazy multisampling” therefore
represents the best compromise between performance
and quality – as long as (u, v)-mapping is not appli-
cable; see Table 3. Multisampling every single pixel
only leads to a computational overhead.
While rendering, most of the time is spent with
shading and – if enabled – intersection testing. The
results for the GPU variant on the other hand are much
more influenced by the OIB creation costs and – in
case of the dynamic robots scene – the scene graph
updates which enforce expensive data texture updates
once per frame.
Another advantage of our OIB ray caster is that
the frame rate remains more or less constant when
rendering animations or fly-throughs, as long as the
entire viewport is filled by the scene, no matter how
the triangles are distributed in space. The curves in
Figure 6 depict the frame rate over time while render-
ing the animated robots scene without multisampling
on the CPU.
0.5
1
1.5
2
2.5
3
0 5 10 15 20 25 30 35 40
FPS
Frame
without shadows
with shadows
Figure 6: The almost constant frame rate, benchmarked on
the slightly slower Xeon workstation (robots scene).
Last but not least we analyse the visual quality.
The results are in most cases encouraging; the differ-
ences between the GPU and CPU based versions are
insignificant. Only if a scene contains many tiny tri-
angles – such as the Stanford bunny – and intersection
testing is enabled, a higher item buffer multisampling
rate is required to produce good results – if there are
Table 4: Frames per second of a traditional ray tracer using
a kd-tree and our hybrid ray tracer (ray depth 3).
Torus Bunny Robots
traditional 0.9 0.6 0.1
traditional, interl. 1.6 1.1 0.1
hybrid 1.6 1.0 0.1
hybrid, interleaved 2.7 1.6 0.2
hybrid, direct 1.6 1.0 0.1
hybrid, direct, interl. 2.8 1.7 0.2
too many such tiny-sized triangles close to each other
visual artefacts are inevitable. We try to overcome
them by shading the missing pixels using colour in-
terpolation. We think that in this case the achieved
quality is fulfilling the expectations – especially for
dynamic scenarios; again see Figure 3.
4.2 Ray Tracing
When ray tracing, our hybrid renderer increases the
rendering performance almost by a factor of 2 com-
pared to a traditional implementation based on a kd-
tree acceleration structure. Interleaved rendering – as
expected – increases the frame rates even more; see
Table 4 for the benchmarks. This speedup is mainly
caused by the efficiency of the OIB ray caster and
due to the parallel execution of the hybrid rendering
pipeline. It is noteworthy that in this case the per-
formance is largely determined by the kd-tree updat-
ing process, which unfortunately can be very slow. In
case of the animated robots scene this takes roughly
2s − 2.5s. It is apparent that in this case the perfor-
mance advantage of the direct renderer is more or less
negligible, instead, additional acceleration techniques
have to be applied to ray trace dynamic scenes (Wald
et al., 2003).
5 CONCLUSION
In this paper we presented the object intersection
buffer (OIB), a graphics hardware accelerated exten-
sion to the item buffer algorithm based on (u, v)-
mapping rather than first hit intersection testing. We
demonstrated that it is feasible to combine the raw
power of GPUs and image-space rendering tech-
niques to accelerate ray tracing. We used the OIB
to implement an interactive ray caster without inte-
grating any spatial acceleration structure. Moreover,
we implemented shadowing using the shadow map-
ping technique instead of shooting shadow rays. This
facilitates the rendering of dynamic scenes at high
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
310

frame rates. We described two implementations of
our ray caster, both accelerated by the graphics hard-
ware. The first one only uses the graphics hardware to
build the OIB and the shadow maps, the second one
executes completely on the GPU. We showed that the
GPU based implementation leads to a superior perfor-
mance. Consequently we used the OIB to implement
a hybrid ray tracer by sharing the load between the
host processor and the GPU using parallel rendering.
ACKNOWLEDGEMENTS
The authors would like to thank Sonja Sch
¨
ar, Stefan
Eilemann, John Hutchison and all other reviewers for
valuable assistance and discussions.
REFERENCES
Bolz, J., Farmer, I., Grinspun, E., and Schr
¨
oder, P. (2003).
The GPU as Numerical Simulation Engine. In Pro-
ceedings of SIGGRAPH 2003. ACM Press.
Buck, I., Foley, T., Horn, D., Sugerman, J., Fatahalian,
K., Houston, M., and Hanrahan, P. (2004). Brook
for GPUs: Stream Computing on Graphics Hardware.
ACM Trans. Graph., 23(3):777–786.
Carr, N. A., Hall, J. D., and Hart, J. C. (2002). The Ray En-
gine. In Proceedings of the ACM SIGGRAPH/EURO-
GRAPHICS conference on Graphics hardware, pages
37–46. Eurographics Association.
Carr, N. A., Hoberock, J., Crane, K., and Hart, J. C. (2006).
Fast GPU Ray Tracing of Dynamic Meshes using Ge-
ometry Images. In GI ’06: Proceedings of the 2006
conference on Graphics interface, pages 203–209.
Christen, M. (2005). Ray Tracing on GPU. Master’s thesis,
University of Applied Sciences Basel.
Fatahalian, K., Sugerman, J., and Hanrahan, P. (2004).
Understanding the Efficiency of GPU Algorithms for
Matrix-Matrix Multiplication. In Graphics Hardware
2004, pages 133–137.
Foley, T. and Sugerman, J. (2005). Kd-Tree Acceleration
Structures for a GPU Raytracer. In HWWS ’05: Pro-
ceedings of the ACM SIGGRAPH/EUROGRAPHICS
conference on Graphics hardware, pages 15–22, New
York, NY, USA. ACM Press.
Heckbert, P. (1986). Survey of texture mapping. IEEE Com-
put. Graph. Appl., 6(11):56–67.
Karlsson, F. and Ljungstedt, C. J. (2004). Ray Tracing Fully
Implemented on Programmable Graphics Hardware.
Master’s thesis, Chalmers University of Technology.
Kim, S., ye Kim, S., and hyun Yoon, K. (2000). A Study
on the Ray-Tracing Acceleration Technique Based on
the ZF-Buffer Algorithm. In IV ’00: Proceedings of
the International Conference on Information Visuali-
sation, page 393, Washington, DC, USA. IEEE Com-
puter Society.
Lamparter, B., M
¨
uller, H., and Winckler, J. (1990). The
Ray-z-Buffer—An Approach for Ray Tracing Arbi-
trarily Large Scenes. Technical Report report00021.
Lefohn, A., Kniss, J. M., Strzodka, R., Sengupta, S.,
and Owens, J. D. (2006). Glift: Generic, Efficient,
Random-Access GPU Data Structures. ACM Trans-
actions on Graphics, 25(1):60–99.
Lext, J., Assarsson, U., and M
¨
oller, T. (2000). BART:
A Benchmark for Animated Ray Tracing. Techni-
cal Report 00-14, Chalmers University of Technology,
Goeteborg, Sweden.
M
¨
oller, T. and Trumbore, B. (1997). Fast, Minimum
Storage Ray-Triangle Intersection. J. Graph. Tools,
2(1):21–28.
Molnar, S., Cox, M., Ellsworth, D., and Fuchs, H. (1994).
A Sorting Classification of Parallel Rendering. IEEE
Computer Graphics and Algorithms, pages 23–32.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M.,
Kr
¨
uger, J., Lefohn, A. E., and Purcell, T. J. (2005).
A Survey of General-Purpose Computation on Graph-
ics Hardware. In Eurographics 2005, State of the Art
Reports, pages 21–51.
Purcell, T. J., Buck, I., Mark, W. R., and Hanrahan,
P. (2002). Ray Tracing on Programmable Graph-
ics Hardware. ACM Transactions on Graphics,
21(3):703–712.
Reshetov, A., Soupikov, A., and Hurley, J. (2005). Multi-
Level Ray Tracing Algorithm. ACM Trans. Graph.,
24(3):1176–1185.
Salesin, D. and Stolfi, J. (1989). The ZZ-Buffer: A Sim-
ple and Efficient Rendering Algorithm with Reliable
Antialiasing. In Proceedings of the PIXIM ’89 Con-
ference, pages 451–66.
Simonsen, L. O. and Thrane, N. (2005). A Comparison of
Acceleration Structures for GPU Assisted Ray Trac-
ing. Master’s thesis, University of Aarhus.
Sutherland, I. E., Sproull, R. F., and Schumacker, R. A.
(1974). A Characterization of Ten Hidden-Surface Al-
gorithms. ACM Comput. Surv., 6(1):1–55.
Wald, I., Benthin, C., and Slusallek, P. (2003). Dis-
tributed Interactive Ray Tracing of Dynamic Scenes.
In Proceedings of the IEEE Symposium on Parallel
and Large-Data Visualization and Graphics (PVG) ,
pages 77–85.
Wald, I. and Havran, V. (2006). On building fast Kd-Trees
for Ray Tracing, and on doing that in O(N log N). In
Proceedings of the 2006 IEEE Symposium on Interac-
tive Ray Tracing, pages 61–69.
Weghorst, H., Hooper, G., and Greenberg, D. P. (1984).
Improved Computational Methods for Ray Tracing.
ACM Trans. Graph., 3(1):52–69.
Weiskopf, D., Schafhitzel, T., and Ertl, T. (2004). GPU-
Based Nonlinear Ray Tracing. In Eurographics 2004,
volume 23, pages 625–633.
Williams, L. (1978). Casting Curved Shadows on Curved
Surfaces. In SIGGRAPH ’78: Proceedings of the 5th
annual conference on Computer graphics and interac-
tive techniques, pages 270–274, New York, NY, USA.
ACM Press.
HYBRID RAY TRACING - Ray Tracing Using GPU-Accelerated Image-Space Methods
311
