
FITTING 3D MORPHABLE MODELS USING IMPLICIT
REPRESENTATIONS
Curzio Basso and Alessandro Verri
DISI, Universit
`
a di Genova, Italy
Keywords:
3D Morphable Models, non-rigid registration, implicit surface representations.
Abstract:
We consider the problem of approximating the 3D scan of a real object through an affine combination of
examples. Common approaches depend either on the explicit estimation of point-to-point correspondences
or on 2-dimensional projections of the target mesh; both present drawbacks. We follow an approach similar
to (Ilic and Fua, 2003) by representing the target via an implicit function, whose values at the vertices of
the approximation are used to define a robust cost function. The problem is approached in two steps, by
approximating first a coarse implicit representation of the whole target, and then finer, local ones; the local
approximations are then merged together with a Poisson-based method. We report the results of applying our
method on a subset of 3D scans from the Face Recognition Grand Challenge v.1.0.
1 INTRODUCTION
We consider the problem of approximating a target
3D surface with an affine combination of (registered)
examples, under the assumption that both the exam-
ples and the target belong to the same object class.
When the assumption holds, the affine space gener-
ated by the examples represents a model of the ob-
ject class, usually known as 3D Morphable Model in
case of faces (Blanz and Vetter, 1999). The model is
parameterized by the coefficients of the affine com-
bination. We consider the class of human faces; our
goal is to find the best possible combination of the
available examples that approximates a given target.
This is essentially a problem of non-rigid registration,
where the available deformations are constrained by
the model; it can arise not only when building a 3D
Morphable Model (Allen et al., 2003; Basso and Vet-
ter, 2006), but also for performing 3D shape analysis
as done for images by (Blanz and Vetter, 2003).
In general, we might approach the problem in dif-
ferent ways, depending on the representation of the
target surface:
• the target is explicitly represented as a triangular
mesh, and the problem is solved in R
3
;
• the target is projected to R
2
, as depth map or
cylindrical projection;
• the target is represented implicitly in R
3
.
The first strategy is essentially based on the Iter-
ated Closest-Point (ICP) registration algorithm (Besl
and McKay, 1992; Turk and Levoy, 1994). Although
originally used for rigid registration, it can be ex-
tended to non-rigid registration and to the case at
hand. This was demonstrated in (Allen et al., 2003),
where the possibility of using examples-based mod-
els was also mentioned. The drawback of this type of
approaches is the need of an explicit estimation of the
point-to-point correspondence between the model and
the target. Letting aside the problems due to holes in
the target, the search for corresponding points in R
3
might be computationally inefficient.
The second approach, adopted by (Blanz and Vet-
ter, 1999) and (Basso and Vetter, 2006), avoids the
explicit estimation of point-to-point correspondences,
by minimizing the difference between the cylindrical
projections to R
2
of the target and the model. As well
as avoiding the direct search for corresponding points,
the projection to R
2
has the advantage of reducing the
problem dimensionality. However, this comes at the
cost of loosing some information about the 3D sur-
45
Basso C. and Verri A. (2007).
FITTING 3D MORPHABLE MODELS USING IMPLICIT REPRESENTATIONS.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 45-52
DOI: 10.5220/0002077200450052
Copyright
c
SciTePress

faces, since the projection is not a parameterization of
the original surface. Moreover, the projection is usu-
ally non-linear and occlusions frequently occur.
In this paper we investigate the possibility of solv-
ing the problem representing the target implicitly in
R
3
. In doing so, we avoid the explicit correspondence
estimation, while still working in the original domain
of the data. Although it has never been applied to
our specific problem, (Ilic and Fua, 2003) have used
an implicit representation to reconstruct surfaces from
uncalibrated video sequences. In their work, how-
ever, it is not the target data that are represented im-
plicitly, but rather the model, a deformable template
that has to be matched to the data. Also related to
ours is the work of (Steinke et al., 2005), where the
problem of registering the target with a fixed template
(not an example-based model) was solved represent-
ing both surfaces implicitly. The implicit represen-
tations where found using Support Vector Machines
(SVM).
Our work is based on a simpler implicit repre-
sentation of the target mesh, based on Radial Basis
Functions (RBF), while the model is still represented
explicitly. The implicit representation defines a sort
of potential field in the space surrounding the target
surface, and can be used to define a robust cost func-
tion. In order to reduce the complexity of computing
the RBF for large meshes, we first minimize the cost
function over a low resolution implicit representation,
and afterward we minimize it over higher resolution
patches of the target. Finally, the different patches are
blended together with a Poisson-editing approach (Yu
et al., 2004). In our work we assume that the target is
already coarsely aligned with the model.
2 BACKGROUND
In the following two subsection we briefly expose
the basic notions our method builds upon: three-
dimensional Morphable Models, and implicit repre-
sentations of surfaces.
2.1 3D Morphable Models
A triangular mesh is defined by a graph M = (V ,E);
V is a set of n vertices in R
3
and E is a set of edges
connecting the vertices. For convenience we write V
as a matrix
V = [v
1
.. .v
n
] =
x
1
.. . x
n
y
1
.. . y
n
z
1
.. . z
n
∈ R
3×n
. (1)
A set of m registered meshes, denoted by M
i
, will
share the same connectivity E but have different ver-
tices positions V
i
. We can naturally define the sub-
space of their affine combinations, with coefficients
a = (a
1
,. .., a
m
) ∈ R
m
, as
M(a) = (V (a), E), (2)
with
V (a) =
m
∑
i=1
a
i
V
i
and
∑
a
i
= 1. (3)
The affine constraint is needed in order to avoid scal-
ing effects.
Note that rewriting eq. (3) in terms of the barycen-
ter
V =
1
m
m
∑
i=1
V
i
, (4)
we can eliminate the constraint on the sum of the co-
efficients:
V (a) = V +
m
∑
i=1
a
i
(V
i
−V ). (5)
Three-dimensional Morphable Models (3DMM) use a
representation for the affine combination based on the
Principal Component Analysis (PCA) of the subspace
spanned by the V
i
−V . Without going into the details
of the PCA (Hastie et al., 2001, pp. 62-63), we only
report that for 3DMM eq. (5) is written as
V (α) = V +
m−1
∑
i=1
α
i
U
i
, (6)
where the U
i
are the principal components and the co-
efficient vector a is replaced by α ∈ R
m−1
. See figure
1 for a simple two-dimensional example.
Assuming the examples are correctly registered,
any rigid transformation has been factored out from
the model. It can be explicitly included by defining a
rotation matrix R and a translation vector t which are
applied to V (α):
V (α,ρ) = R(ρ) ·
(
V +
m−1
∑
i=1
α
i
U
i
)
+t(ρ) ⊗ 1
T
n
, (7)
where the last term is simply an n-times repetition of
the column vector t. R and t are parameterized by a
vector ρ ∈ R
6
, holding the coefficients of the transfor-
mation (three for the rotation and three for the trans-
lation). Taking into account the rigid transformation,
the model is defined by M(α,ρ) = (V (α,ρ),E).
2.2 Implicit Representations of 3D
Surfaces
An implicit representation of a given surface T ⊂ R
3
is a function F
T
: R
3
→ R such that the surface is one
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
46

of its level sets. That is, F
T
(v) = h for each v ∈ T , and
F
T
(v) 6= h otherwise, where h is a constant, typically
zero. Clearly, an example of implicit representation is
the Euclidean distance
F
T
(v) = min
w∈T
kv − wk. (8)
In order to define a cost function based on such
an implicit representation, we are interested in an an-
alytic form for the implicit function F
T
; we build it
following the lines of (Turk and O’Brien, 1999; Carr
et al., 2001). Given a certain 3D mesh, they look for
a function F(v) which is zero on the vertices and dif-
ferent from zero on a set of off-surface points. The
off-surface points are required to avoid the trivial so-
lution of a function identically zero over the whole
space. They are chosen to lie on the normal to the
surface at the mesh vertices. Let us denote by w
j
the
vertices and the off-surface points. Then, given a ra-
dial basis function φ(x), there exist a choice of scalar
weights d
j
and of a degree one polynomial P(v) such
that the function
F(v) =
n
∑
j=1
d
j
φ(v − w
j
) + P(v), (9)
satisfies the constraints F(w
j
) = h
j
and is also
smooth, in the sense that minimizes the energy
E =
Ω⊂R
3
F
2
xx
+ F
2
yy
+ F
2
zz
+ 2F
2
xy
+ 2F
2
yz
+ 2F
2
zx
, (10)
a generalization to R
3
of the thin-plate energy. In fig-
ure 1 we show such an example of F
T
(v), where T is
a poly-line in 2D.
In practice, the unknown vectors d and p (coeffi-
cients of the polynomial) are the solutions of a linear
system. Given the matrices
Φ =
φ
11
.. . φ
1n
.
.
.
.
.
.
φ
n1
.. . φ
nn
(11)
and
A =
1 x
1
y
1
z
1
.
.
.
.
.
.
.
.
.
.
.
.
1 x
n
y
n
z
n
(12)
one has to solve the system
Φ A
A
T
0
d
p
=
h
0
. (13)
Note that when the input mesh is large, the above
linear system, if dense, might become intractable. A
possible solution is to induce sparsity by choosing a
basis with compact support, but this on turn creates
extrapolation problems. In order to maintain spar-
sity and achieve good extrapolation behavior an op-
tion is to define multiple levels of resolution, as done
by (Ohtake et al., 2003). Without resorting to a com-
pact support basis, one can use Fast Multipole Meth-
ods to reduce both the storage and the computational
cost, as done in (Carr et al., 2001).
3 LOW RESOLUTION
APPROXIMATION
Given a 3DMM M(α,ρ) as defined in section 2.1,
and a target mesh T , we formulate the approximation
problem as the optimization
α
?
,ρ
?
= argmin
α,ρ
D(M(α,ρ),T ), (14)
where D is a suitable function measuring the approx-
imation cost.
Assuming we have an implicit representation F
T
for the target mesh, we can define the cost of approx-
imating T by M(α,ρ) as
D(M(α,ρ),T ) =
1
N
N
∑
i=1
`(F
T
(v
i
)), (15)
where the v
i
are the vertices of M(α,ρ), and ` might
be a quadratic loss or an M-estimator. The choice of
an M-estimator might be necessary when parts of the
model M are not present in the target T and influence
the correct approximation of the rest. Observe that
in the above definition we are essentially treating the
values F
T
(v
i
) as residuals of the approximation. In
fact, if F
T
was the Euclidean distance function and
`(x) = x
2
, then D would correspond to an `
2
norm.
3.1 Optimization Scheme
In order to find the minimum of the cost function (15),
we use a modified Newton’s method. For the sake
of clarity, in the following discussion we denote by
θ the vector of all model coefficients, without distinc-
tions between α and ρ. Recall that the exact Newton’s
method consists in iteratively updating θ by adding
the solution p of the linear system
∇
2
D(θ) · p = −∇D(θ), (16)
where ∇
2
D(θ) denotes the Hessian matrix of D at θ.
The exact method converges to a minimum of D when
sufficiently close to it, but it does not in general; nev-
ertheless, there are a number of standard modifica-
tions that make it more efficient and robust. We em-
ploy a simple scheme, which keeps the Hessian ma-
trix sufficiently positive definite by adding a multiple
FITTING 3D MORPHABLE MODELS USING IMPLICIT REPRESENTATIONS
47
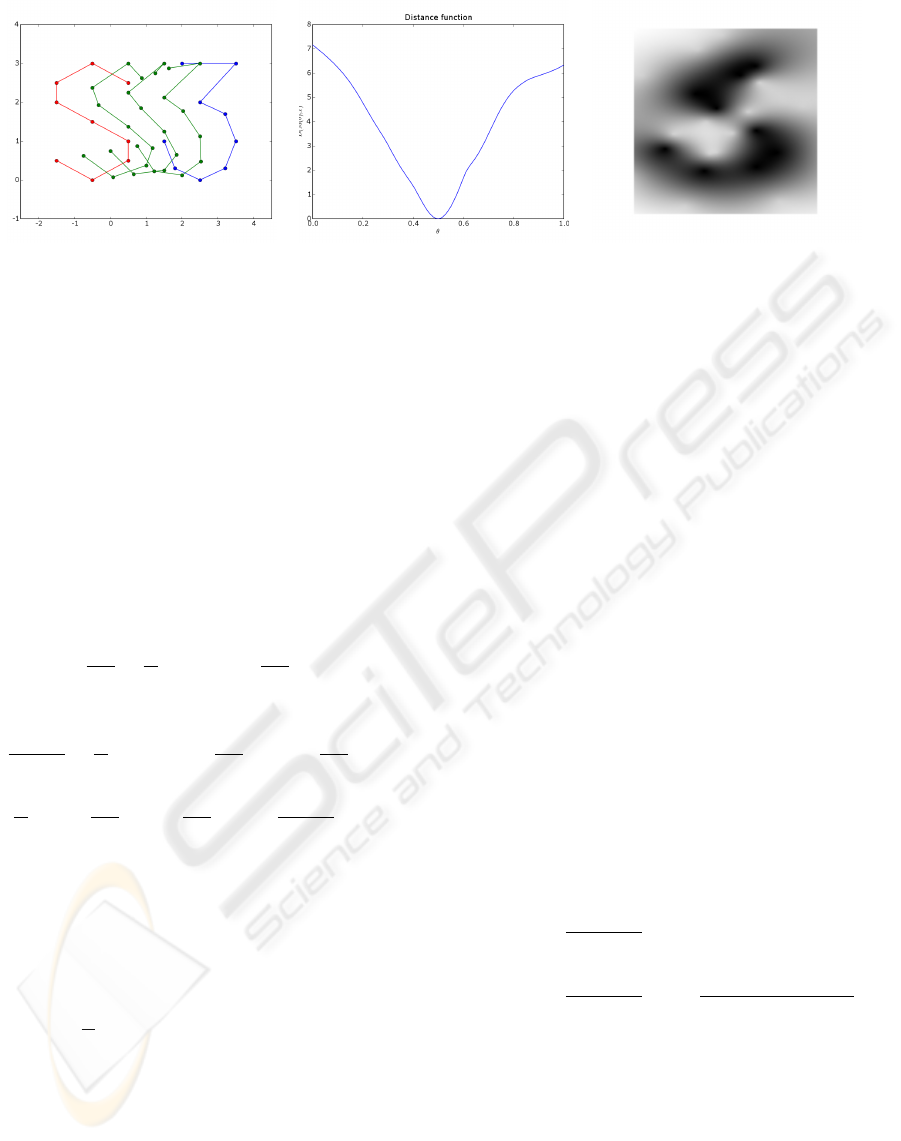
Figure 1: On the left, an example of a 2D morphable model M(α): two poly-lines, in red and blue, representing the characters
’S’ and ’3’. The green curves are linear combinations of the two examples, and can be written as the average shape plus a
deformation along the only principal direction. The amount of the deformation is given by the coefficient α, whose values for
the three green curves are respectively α = {−0.5,0, 0.5}. If we consider the average shape (α = 0), it generates the implicit
representation on the right, where the gray-levels correspond to the values of F
T
(x), as defined by eq. (9) with φ(x) = kxk.
The figure in the middle shows the corresponding cost function D(M(α),T ) as defined by eq. (15) with `(x) = x
2
.
of the identity when required (Nocedal and Wright,
1999, Ch.6.3). Another modification to the exact
method is that the update length is not unitary, but
it is determined by a backtracking procedure which
reduces the length if the update does not reduce D
(Nocedal and Wright, 1999, Ch.3.1).
Having the exact form of the implicit represen-
tation allows us to compute analytically the gradient
and the Hessian matrices of the cost function:
∂D
∂θ
j
=
1
N
N
∑
i=1
`
0
i
∇F
i
·
∂v
i
∂θ
j
, (17)
and
∂
2
D
∂θ
j
∂θ
k
=
1
N
N
∑
i=1
`
00
i
∇F
i
·
∂v
i
∂θ
j
∇F
i
·
∂v
i
∂θ
k
+
1
N
N
∑
i=1
`
0
i
∂v
i
∂θ
j
· ∇
2
F
i
·
∂v
i
∂θ
k
+ ∇F
i
·
∂
2
v
i
∂θ
j
∂θ
k
. (18)
In the above equations we used `
0
i
and `
00
i
to denote the
first and second derivatives of the loss function com-
puted at F
T
(v
i
); ∇F
i
and ∇
2
F
i
denotes the gradient
vector and the Hessian matrix of F
T
with respect to
the spatial coordinates, computed at v
i
.
In practice we choose ` to be the Tukey estimator,
that is
`(x) =
(
c
2
6
h
1 −
1 − (x/c)
2
3
i
if|x| ≤ c
c
2
/6 otherwise
(19)
with derivatives
`
0
(x) =
(
x
1 − (x/c)
2
2
if|x| ≤ c
0 otherwise
(20)
`
00
(x) =
(
1 − 5(x/c)
2
1 − (x/c)
2
if|x| ≤ c
0 otherwise
(21)
Note that the effectiveness of the Tukey estimator in
reducing the influence of model vertices not present
in the target depends on the scale of the constant c:
the smaller the constant, the smaller the influence of
missing vertices. On the other hand, small c’s require
a good pre-alignment of the model with the target. In
all our experiments we used c = 5.0.
The gradient and Hessian of F
T
depends on the
choice of the basis φ. Following (Carr et al., 2001), we
use the biharmonic basis function φ(x) = kxk, which
results in the smoothest solution to the interpolation
problem among all radial basis functions. Such a
function with non-compact support is also more suit-
able to inter- and extrapolation. The derivatives are
easily computed
∇φ(x) = x/φ, (22)
∇
2
φ(x) =
I
3
− ∇φ · ∇φ
T
/φ. (23)
Accordingly, we have
∇F
i
=
n
∑
j=1
d
j
kv
i
− w
j
k
(v
i
− w
j
) + (p
1
, p
2
, p
3
), (24)
∇
2
F
i
=
n
∑
j=1
d
j
kv
i
− w
j
k
I
3
−
(v
i
− w
j
)(v
i
− w
j
)
T
kv
i
− w
j
k
2
.
(25)
3.2 Regularizing Prior
In many cases, in particular to avoid overfitting, it
might be convenient to add to the cost function (15) a
regularization term which penalizes excessively large
model coefficients:
D
R
= D + η
α
E(α) + η
ρ
E(ρ), (26)
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
48

Figure 2: Examples of input data and the results of each approximation step. On the left column are shown the target (top
image) and the implicit representation of its subsampling (bottom). Fitting the model to the latter results in the shape in the
middle column, top image. The next step consist in separately fitting the segments of the model, shown in the bottom-center
image, to corresponding parts of the target. The result is shown in the right column: on the top are the different approximations
stitched together, on the bottom the result of blending them.
where the parameters η
α
and η
ρ
weight the effect of
the regularization on the shape and the rigid parame-
ters, respectively.
A standard way to choose the regularization terms
consists in deriving them from prior probabilities. In
the case of the shape coefficients, the PCA model
assumes for α a normal distribution with unit vari-
ance; for the rigid coefficients we also assume a Gaus-
sian distribution with zero mean, but with empiri-
cally chosen variances. In both cases, we can define
a regularization term proportional to the inverse log-
likelihood. For a generic coefficient θ with variance
σ
2
we have
−log p(θ) =
θ
2
2σ
2
+ const. (27)
so that we set (Σ
ρ
is the diagonal covariance matrix
for the rigid coefficients)
E(α) =
1
2
kαk
2
and E(ρ) =
1
2
ρ
T
Σ
−1
ρ
ρ. (28)
4 SEGMENTED
APPROXIMATION
As noted in section 2.2, a direct solution of the inter-
polation problem by solving the linear system is com-
putationally and storage intensive. In fact, for high
resolution target meshes, the system is too large to be
allocated in memory. Rather than following one of
the methods mentioned in section 2.2, we decided to
overcome the problem by adopting a simpler multi-
resolution approach (refer to figure 2 for examples of
the intermediate steps outputs):
1. Coarse Approximation. We first compute a
coarse approximation of the target. We select a
subset of the target mesh vertices, sampled with
probabilities proportional to the areas of the ad-
joining triangles, and use them as constraints of
the interpolation problem. The resulting implicit
surface is fit with the procedure described in the
previous section.
2. Partitioning. Once we have obtained the coarse
approximation of the target, we can achieve a
higher resolution by repeating the process on
FITTING 3D MORPHABLE MODELS USING IMPLICIT REPRESENTATIONS
49
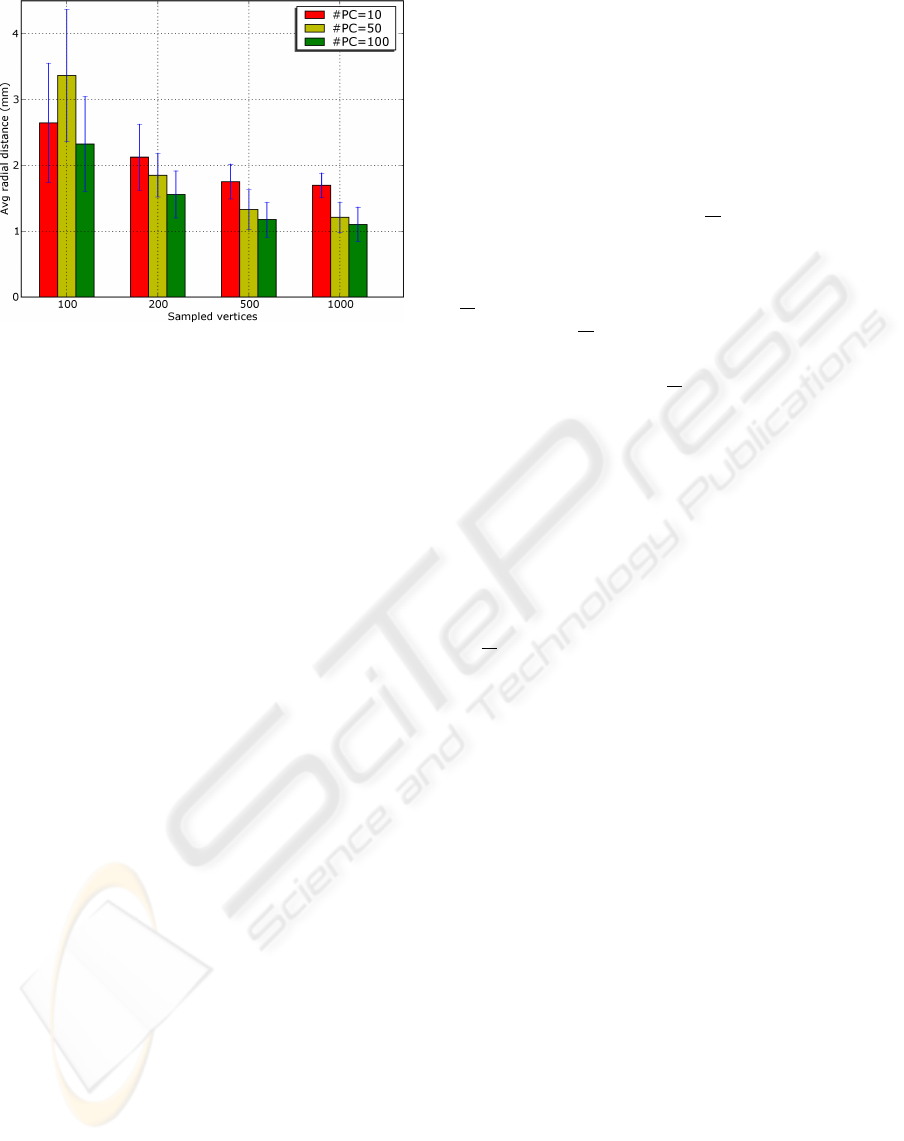
Figure 3: Dependency of the approximation on the number
of principal components used by the model and the number
of vertices sampled from the target surface.
smaller patches of the target and finally merging
the local approximations. To this aim, we manu-
ally defined four regions on the model topology;
the regions are visible in figure 2, middle image
of the bottom row. Given the coarse approxima-
tion, we compute the bounding box of each re-
gion, we expand it in all directions by a fixed
length (2 cm in our experiments), and select all the
target’s vertices falling inside the box. This results
in four overlapping subsets of the target vertices,
each one associated with a different segment of
the model.
3. Finer Approximations. For each subset of the
target vertices we build an (approximate) implicit
representation by sampling its vertices as done
in step 1. Although the subsets are again sub-
sampled, the ratio between the number of sampled
vertices and the total number of vertices clearly
increases, resulting in a more precise representa-
tion. The implicit surfaces are fit again with the
usual procedure.
4.1 Blending
It is clear that the approximation method explained in
the previous section provides local results, which do
not match precisely at their boundaries. In order to
merge them smoothly, we use a variational approach
akin to the Poisson-based mesh editing of (Yu et al.,
2004), to which we refer for more details. The main
idea is to keep fixed the positions of the vertices in the
interiors of the segments and let the other vertices re-
lax to the positions which minimize an elastic energy.
The procedure is as follows:
1. identify the boundaries of the patches;
2. for each vertex, compute its minimum distance
from the boundaries, by fast marching (Kimmel
and Sethian, 1998);
3. define the interior as the set of vertices with dis-
tance greater than a certain threshold (we used 0.5
cm);
Steps 1 to 3 define the mesh interior Ω and its com-
plement, the boundary region
Ω: an area with given
width that surrounds the segments boundaries. We
denote by ∂Ω the set of vertices in the interior Ω that
are connected to any vertex in the boundary region
Ω. While the vertices in Ω are fixed, the positions of
the vertices in Ω are obtained by solving the Poisson
equation:
4. for all the vertices in Ω, find their position solv-
ing a discretized Poisson equation using as bound-
ary conditions the positions of the vertices in ∂Ω
and as guidance field the gradient of the coarse
approximation.
In practice, one solves the Poisson equation for the
field of displacements from the coarse approximation
to the fine one. This formulation yields a sparse linear
system of equations of the type ∆d
i
= 0, where ∆ is the
discrete Laplacian operator over the mesh (Taubin,
1995), and d
i
is the displacement of the i-th vertex
in Ω. The system is solved under the boundary con-
straints at ∂Ω, where the displacements are known.
5 RESULTS
The above method has been tested using as model a
sub-sampled version of the mixed expression-identity
3D Morphable Model built with the algorithm de-
scribed in (Basso and Vetter, 2006). The sub-
sampling is simple, since the reference template was
built by subdivision of a low-resolution one. Out of
around 40k vertices at full resolution, we retained ap-
proximately 2.5k. As well as reducing the number
of vertices, we also discarded the expression shape
components and all the texture components. The tar-
gets were a set of 165 range scans, randomly sampled
from the range data distributed for the Face Recog-
nition Grand Challenge v.1.0 (Phillips et al., 2005).
The scans were distributed with a list of landmark po-
sitions, which we used to pre-align the faces to the
model. The approximations have been performed us-
ing 99 model components and 500 sampled vertices
for building the implicit representations. We should
remark that these are preliminary experiments, and a
more in-depth study will follow.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
50

Figure 4: Some examples of approximations (bottom row, the original are on the top row). The average per-vertex radial
errors for the three examples are, respectively: 0.80, 0.86 and 0.80 mm.
We evaluated the goodness of the fit by cylindri-
cally projecting the target and the approximation, and
computing the average absolute error (a radial dis-
tance) on the four segments. The rest of the head
model was not taken into account because of the hair
and clothes often present in the scans. Of the 165 re-
sults, we rejected three of them in which the error was
more than three standard deviations larger than the av-
erage. In the remaining 163 results, the average radial
error was 1.09 mm on the blended high-resolution re-
sult, with an average improvement with respect to the
low resolution approximation of 0.39 mm. Some of
the results are shown in figure 4.
We also ran a small experiment to assess the de-
pendency of the approximation on the number of prin-
cipal components used and the number of vertices
sampled from the target surface. We repeatedly com-
puted the low resolution approximations for a small
subset of test data (only four examples), varying the
two aforementioned parameters. The results are in
figure 3. The dependency on the number of principal
components used in the model behaves as expected:
up to a point, the more components are used the bet-
ter the approximation performance. This is not true
anymore when input is too noisy, as it probably oc-
curs when the number of sampled vertices is only 100.
More interestingly, the dependency on the number of
sampled vertices shows that an increase on the sample
rate pays off only up to a point, while the improve-
ment from 500 to 1000 is minimal.
6 CONCLUSION
We have presented a method which makes simple use
of the implicit representation of a surface to find its
optimal approximation in terms of an affine combi-
nation of examples. Implicit representations are ap-
pealing in general, because they are topology-free and
typically quite robust to holes in the data. In our
setting, they also offer the advantage of completely
avoiding the problem of estimating correspondences.
As we saw, however, the use of implicit rep-
resentations poses serious computational problems
when dealing with high-resolution meshes. There-
fore, we have proposed to tackle the problem in a
multi-resolution fashion, and we have shown how this
approach can provide good results without comput-
ing full-resolution representations. We should remark
that, in assessing the method, we considered its per-
formance only in absolute terms, without comparing
it with respect to other, already published algorithms.
FITTING 3D MORPHABLE MODELS USING IMPLICIT REPRESENTATIONS
51

This is certainly a deficiency of our work, and we
will have to correct it in the future. Nevertheless,
we believe that the absolute performance achieved by
our method on the Face Recognition Grand Challenge
range data is a strong indicator of its applicability to a
real-world scenario.
The sub-sampling of the original surface is further
motivated by the consideration that the model has also
a fixed level of resolution. The resolution of the model
does not only dependent on the number of vertices of
its mesh, but especially on the number of training ex-
amples and of components used. It seems therefore
reasonable to tweak the resolution of the target so that
it matches the one of the model. On the other hand,
sub-sampling poses problems. This is particularly
clear when considering the approximation results ob-
tained on targets containing clothes or hairs. In the
best case these data are irrelevant, in the worst they
are harmful, since they will cause distortions in the
low-resolution implicit representation, which might
be enhanced by an unlucky sub-sampling. Prepro-
cessing of the targets which removes these data would
certainly improve the method’s performance and sta-
bility.
The future development will focus on two prob-
lems: first, the choice of the optimal segments in
which the model is partitioned, and second, the in-
tegration of a texture model in the approximation
scheme.
ACKNOWLEDGEMENTS
This work has been partially supported by the FIRB
project RBIN04PARL.
REFERENCES
Allen, B., Curless, B., and Popovic, Z. (2003). The space
of human body shapes: reconstruction and parameter-
ization from range scans. In Proc. ACM SIGGRAPH
03.
Basso, C. and Vetter, T. (2006). Registration of expressions
data using a 3d morphable model. Journal of Multi-
media, 1(4):37–45.
Besl, P. and McKay, N. (1992). A method for registration
of 3-d shapes. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 14(2):239–256.
Blanz, V. and Vetter, T. (1999). A morphable model for the
synthesis of 3d faces. In Proc. ACM SIGGRAPH 99,
pages 187–194. ACM Press.
Blanz, V. and Vetter, T. (2003). Face recognition based on
fitting a 3d morphable model. IEEE Trans. Pattern
Anal. Mach. Intell., 25(9):1063–1074.
Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,
Fright, W. R., McCallum, B. C., and Evans, T. R.
(2001). Reconstruction and representation of 3d ob-
jects with radial basis functions. In Proc. of ACM
SIGGRAPH 2001.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The
Elements of Statistical Learning. Springer Series in
Statistic. Springer.
Ilic, S. and Fua, P. (2003). Implicit meshes for modeling
and reconstruction. In Proc. Conf. Computer Vision
and Pattern Recognition 2003.
Kimmel, R. and Sethian, J. (1998). Computing geodesic
paths on manifolds. Proc. Natl. Acad. Sci. USA,
95(15):8431–8435.
Nocedal, J. and Wright, S. J. (1999). Numerical Opti-
mization. Springer Series in Operations Research.
Springer.
Ohtake, Y., Belyaev, A., and Seidel, H.-P. (2003). A
multi-scale approach to 3d scattered data interpola-
tion with compactly supported basis functions. In SMI
’03: Proceedings of the Shape Modeling International
2003, page 153, Washington, DC, USA. IEEE Com-
puter Society.
Phillips, P. J., Flynn, P. J., Scruggs, T., Bowyer, K. W.,
Chang, J., Hoffman, K., Marques, J., Min, J., and
Worek, W. (2005). Overview of the face recogni-
tion grand challenge. In Computer Vision and Pattern
Recognition (CVPR 2005), volume 1, pages 947–954,
Los Alamitos, CA, USA. IEEE Computer Society.
Steinke, F., Scholkopf, B., and Blanz, V. (2005). Support
vector machines for 3d shape processing. Computer
Graphics Forum, 24(3):285–294.
Taubin, G. (1995). A signal processing approach to fair
surface design. In SIGGRAPH ’95: Proceedings
of the 22nd annual conference on Computer graph-
ics and interactive techniques, pages 351–358, New
York, NY, USA. ACM Press.
Turk, G. and Levoy, M. (1994). Zippered polygon meshes
from range images. In SIGGRAPH ’94: Proceedings
of the 21st annual conference on Computer graph-
ics and interactive techniques, pages 311–318, New
York, NY, USA. ACM Press.
Turk, G. and O’Brien, J. F. (1999). Shape transformation
using variational implicit functions. In Proc. of ACM
SIGGRAPH 99.
Yu, Y., Zhou, K., Xu, D., Shi, X., Bao, H., Guo, B., and
Shum, H.-Y. (2004). Mesh editing with poisson-based
gradient field manipulation. In Slothower, D., edi-
tor, Proc. ACM SIGGRAPH 04, pages 641–648. ACM
Press.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
52
