A HYBRID BACKWARD-FORWARD METHOD FOR

INTERACTIVE REFLECTIONS

Chunhui Mei, Voicu Popescu and Elisha Sacks

Computer Science Department, Purdue University, 305 N University Street, West-Lafayette, USA

Keywords: Reflection rendering, interactive frame rates, projection, ray-tracing, k-d tree, continuous 3-ray camera.

Abstract: We propose a two phase hybrid reflection rendering method based on approximating the reflected rays with

a set of simple cameras modeled as continuous 3-ray cameras. In the first, "backward", phase, the view

volume of each simple camera is intersected with a hierarchical subdivision of the scene to find the

geometry it encompasses. In the second, "forward", phase the geometry is projected with the simple camera.

Since the shape and topology of reflected triangles is complex, point based rendering is adopted to

reconstruct the reflection. The hybrid method is efficient since it combines advantages of backward and

forward techniques: there are two orders of magnitude fewer simple cameras than reflected rays, the

hierarchical scene subdivision implements fast view volume culling for each of the simple cameras, and the

reflection piece corresponding to each simple camera is computed efficiently in feed-forward fashion.

1 INTRODUCTION

Reflective surfaces are the first to draw the attention

of a user that visually explores a 3D scene. In

addition to intriguing aesthetic quality, reflections

bring concrete contributions to the user’s

understanding of the scene, revealing surface

properties and the relative position of objects.

Unfortunately, rendering reflections is challenging.

The difficulty comes from the fact that every

reflective surface is essentially a portal into a world

that is potentially more complex than the directly

observed scene. In the reflected scene the rules of

image formation are substantially more complex

than those in the case of single perspective: a 3D

point can have more than one projection, straight

lines project to curves, some surfaces are magnified

and others minified to the extreme. Much work has

been devoted to rendering reflections, but no

technique exists that renders accurate reflections on

general surfaces at interactive rates. We group prior

techniques in four categories.

Ray tracing techniques search for scene

geometry along desired view and reflected rays.

Such techniques produce breathtaking reflections,

but the backward mapping from the output pixels to

input geometry is inefficient, and ray tracing is not

the approach of choice in interactive graphics. The

feed-forward graphics pipeline, with the main stages

of projection and rasterization, has proven to be the

best suited for computer graphics applications where

efficiency is at a premium. However, rendering

reflections with the feed-forward approach requires

solving the difficult problem of projecting reflected

vertices. For a general reflector surface there is no

closed form solution to the problem of finding the

image plane location of a reflected 3D point. Feed-

forward techniques were developed for planar and

convex reflectors, cases when the problem of

projecting reflected vertices is tractable.

Reflected-scene approximation techniques

intersect reflected rays with a simpler version of the

scene, in the interest of efficiency. A prime example

is environment mapped reflections, where the

reflected scene is replaced with a distant color

panorama. Less drastic approaches simplify the

scene using billboards or depth map impostors. The

disadvantages of the approach are loss of accuracy

and additional modeling burden.

Image-based rendering (IBR) techniques employ

pre-acquired or pre-rendered reference reflections to

reconstruct the reflections in the desired view. The

forte of these techniques is the visual realism

inherited from photographs or from reference

images elaborately rendered offline. Disadvantages

include limited support for highly reflective

284

Mei C., Popescu V. and Sacks E. (2007).

A HYBRID BACKWARD-FORWARD METHOD FOR INTERACTIVE REFLECTIONS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 284-292

DOI: 10.5220/0002076802840292

 SciTePress

surfaces, which require a high sampling rate, and

limited support for dynamic scenes, where reference

reflections become obsolete.

In this paper we describe a hybrid technique that

combines elements characteristic to ray tracing with

feed-forward rendering. The desired view and the

reflectors in the scene define a set of reflected rays

for each frame. Depending on frame resolution and

on how much of the frame is covered by reflectors,

the set of reflected rays can contain hundreds of

thousands of rays. Our technique approximates these

rays with a few thousand simple cameras by taking

advantage of the local coherence exhibited by the

ray set. A simple camera is an atomic camera that

has an efficient projection function. A simple

camera could be modeled as a planar pinhole

camera, but the reflected rays are not concurrent and

forcing them through a pinhole introduces large

errors. We use instead a continuous 3-ray camera

(C3RC) (Popescu et al., 2006), a non-pinhole model

that interpolates between 3 given rays. The C3RC is

a generalization of the general linear camera (Yu

and McMillan, 2004), with the advantage of

projection continuity across shared edges of adjacent

cameras.

In a first phase, the view volume of each C3RC

is intersected with the scene to find the geometry it

encompasses. This backward mapping phase is

common to ray tracing techniques, and we accelerate

it using a kd-tree (Bentley, 1979) scene subdivision.

The kd-tree ensures efficient frustum culling for the

C3RCs.

In a second phase, the reflection is computed in

feed-forward fashion. Each simple camera renders

the geometry inside its view volume to produce a

piece of the reflection. Although the reflected

objects are modeled with triangle meshes,

conventional vertex projection followed by projected

triangle rasterization is complicated by several

factors. First, a vertex could have more than one

projection, even within a single C3RC. Second, the

view volume of the C3RC is complex and triangle

clipping is expensive. Third, the edges of the

projected triangles are curved, which requires

subdividing the triangle such that its projected edges

can be acceptably approximated with straight

Figure 1: Objects reflected with our technique. The reflector complexity [thousands of triangles], reflected objects total

complexity [thousands of vertices], and average frame rate [fps] are 4, 74, and 5 for the left image, and 2, 100, and 4 for the

middle image. The reflection of the objects is rendered in point-based fashion, as illustrated in the right image.

Figure 2: Comparison to environment mapping. Environment mapping (left) is inaccurate for objects close to the reflector.

Our technique (middle) produces correct reflections even if the object intersects the reflector (right).

A HYBRID BACKWARD-FORWARD METHOD FOR INTERACTIVE REFLECTIONS

285

segments. A point-based representation of the

reflected objects bypasses these challenges. As a

preprocess we sample the reflected geometry and

store the points in the kd-tree. At run time the points

are splatted using the C3RC to form the reflection.

The two phase backward-forward approach

produces quality reflections at interactive rates, see

Figure 1, 2, and 5, and the accompanying video. The

method has an efficiency advantage over ray tracing

because there are two orders of magnitude fewer

C3RCs than there are reflected rays, and because the

geometry within the view volume of a C3RC is

processed efficiently in feed-forward fashion.

Compared to a naïve feed-forward approach that

renders each triangle with each of the C3RCs, our

method benefits from the view volume culling

provided by the hierarchical scene subdivision.

2 PRIOR WORK

Image-based rendering

Light fields (Levoy and Hanrahan, 1996), are the

most powerful IBR primitive and they naturally

support reflections. Light fields can be used to

render reflections in one of several ways. The light

field can directly provide the desired view ray—it

does not matter whether the ray was reflected one or

several times on its path from the light source to the

eye. Another approach is to use a surface light field

(Miller, 1998), (Wood et al., 2000) attached to the

reflector in which to lookup the desired view rays

that intersect the reflector. A third possibility is to

surround the reflector with a conventionally

parameterized light field and to look up the reflected

ray, a technique called light field mapping (Yu and

McMillan, 2005). A fourth approach is based on

decoupling reflector properties from illumination.

This is achieved with a light field that maps incident

rays to reflected rays (Heidrich, 1999), or to a set of

radiance environment maps (Cabral and Olano,

1999).

Several techniques have been developed for

rendering reflective surfaces from 2D ray databases,

such as view dependent texture mapping (Debevec

et al., 1998), or parameterized environment maps

(Hakura, 2001). A disadvantage common to all IBR

reflection rendering techniques is the lack of support

for dynamic scenes: if the reflecting or reflected

objects move, or if the lighting conditions change,

the reference rays become obsolete. A second

disadvantage is limited support for highly reflective,

mirror-like surfaces, which require a high sampling

rate and generate impractically large ray databases.

Feed-forward methods

These methods set out to solve the reflected-point

projection problem, in order to make reflection

rendering tractable in the context of the feed-forward

pipeline. Projection is simple in the case of planar

reflectors (Diefenbach, 1996), but it does not have a

closed form solution in the case of curved reflectors.

Explosion maps (Ofek and Rappoport, 1998) and

sample-based cameras (Popescu et al., 2006) tackle

the projection problem for curved reflectors.

Explosion maps need to be recomputed for every

frame, which is inefficient, and the projection of

reflected vertices is approximate.

Sample-based cameras are similar to our method,

so we describe them in more detail. For each frame,

the set of reflected rays is partitioned recursively in

sets that are small enough such that they can be

approximated well with a planar pinhole camera. An

approximation is considered acceptable if the

projection error is below a user specified threshold,

typically 1 to 5 pixels. The planar pinhole cameras

are stored at the leafs of a binary space partitioning

tree (BSP), which is called a sample based camera

(SBC). The reflection is rendered with the SBC by

projecting scene vertices and then by rasterizing the

resulting triangles in pure feed-forward fashion. In

order to avoid excessive redundancy during the BSP

construction and inefficiency during projection, the

view frusta of the planar pinhole cameras need to be

disjoint. This condition is only satisfied by convex

reflectors, which is a severe limitation.

Our method does not require the view frusta of

the simple cameras (C3RCs in our case, planar

pinhole cameras in the case of SBCs) to be disjoint,

since, instead of partitioning the view frusta, we

partition the scene to be reflected. The SBC is a

compound camera which finds the simple camera

that contains a given point in logarithmic time. The

first phase of our method on the other hand is similar

to ray tracing in that it iterates over all simple

cameras and finds the geometry each of them sees in

logarithmic time. The advantage is lifting the

limiting condition that the reflector be convex.

Ray tracing

Ray tracing (Whitted, 1980), (Glassner, 1989) is a

general rendering technique that produces high

quality reflections. In the context of interactive

graphics, the challenge is performance. A wide

range of acceleration schemes have been proposed,

and ray tracing has been shown to run at interactive

rates on shared memory parallel computers (Parker,

1999), on special hardware (Hall, 2001), on a single

CPU (Wald, 2001), (Wald et al., 2001), (Reshetov et

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

286

al., 2005), and on GPUs (Purcell et al., 2002), (Carr

et al., 2002), (Weiskopf et al., 2004). At least for the

foreseeable future, GPUs will remain a primarily

feed-forward rendering engine. Therefore,

techniques like ours that attempt to cast the problem

of reflections in terms suitable for feed-forward

rendering will continue to best leverage GPUs.

Reflected-scene approximation methods

First order reflected rays can be easily computed

with the feed-forward graphics pipeline: the reflector

is processed like any geometry and per-pixel

reflected rays are computed using per-pixel normals.

Per-pixel normals are computed by interpolating

vertex normals, by perturbing interpolated normals

according to a bump map, or by looking up a normal

map. The problem is to intersect the scene with the

reflected ray. Several techniques solve this problem

by approximating the reflected scene. Environment

mapping (Blinn and Newell, 1976), (Greene, 1986)

is the classic example.

The reflected scene can be modeled with layered

depth images (LDIs) (Shade et al., 1998), and,

although ray tracing LDIs is less expensive than ray

tracing the entire scene, performance remains an

issue (Lischinski and Rappoport, 1998). A more

efficient method models the reflected scene with a

sphere of size comparable to size of the environment

(Bjorke, 2004). The disadvantage is that the sphere

is a crude approximation of the environment, which

translates in reflection inaccuracy. A cube map with

per-texel depth provides a tighter reflected scene

approximation (Szirmay-Kalos et al., 2005).

However, the impostor-ray intersection algorithm

makes drastic simplifying assumptions precluding

complex scenes.

3 ALGORITHM OVERVIEW

Given a scene of reflectors and diffuse nearby

objects, the algorithm proceeds as follows.

3.1 Preprocessing

In order to support point-based rendering of the

reflection, the diffuse geometry is pre-sampled

uniformly. One of the challenges of point-based

rendering is hole-free reconstruction. One advantage

specific to reflections is that the distance from the

reflected object to the reflector places a lower bound

on the distance between the viewpoint and the point-

based rendered object.

Another advantage is that curved reflectors

typically minify the reflected object, which reduces

the required sampling rate. Even for concave

reflectors there is only a relatively small region of

space where rays are condensed. After the quasi-

convergence region rays diverge again. When a

reflected object is placed in the quasi-convergence

region, point-base reconstruction is challenging.

Front surface opacity can be maintained by

increasing the splat size during rendering. For the

examples shown in this paper it was easy to find

sampling rates that do not leave holes even for small

splat sizes, which ensures a quality reconstruction.

Once the diffuse triangle meshes are sampled,

reflections are rendered from the set of diffuse

points and the reflector triangle meshes with the

following run-time algorithm.

3.2 Run-time

For each frame

Build a kd-tree K for the diffuse point set (Section 4).

Construct C3RCs for each triangle of each reflector

mesh (Section 5).

For each C3RC C

Intersect view volume V of C into K to find the

set S of leafs of K that intersect V (Section 5.2).

For each leaf L in S (Section 6)

For each point P in L

Project P with C to P’ (Section 5.1)

Rasterize P’

4 KD-TREE CONSTRUCTION

We use a standard kd-tree to organize the diffuse

point set hierarchically. The termination criterion for

the recursive construction of the tree is reaching a

minimum number of points or a minimum size for

the leaf node. For simple diffuse objects the kd-tree

construction is fast enough to be performed on the

fly. Higher complexity diffuse point sets are

partitioned off-line. A kd-tree remains valid under

rigid body transformations.

5 CONTINUOUS 3-RAY CAMERA

C3RCs are the mechanism for taking advantage of

reflected ray coherence. A C3RC is built for each

reflector triangle, replacing the reflected rays

generated by that triangle. A C3RC interpolates

A HYBRID BACKWARD-FORWARD METHOD FOR INTERACTIVE REFLECTIONS

287

between 3 construction rays of unit length (Popescu

et al., 2006). The 3 rays are the reflected rays at the

vertices of the reflector triangle (Figure 3). Given

the normal at the vertex and the desired viewpoint,

the reflected ray can be easily computed. The C3RC

image plane is defined by the tails of the 3

construction rays, thus it coincides with the reflector

triangle that generated the C3RC. The C3RC model

is based on the general linear camera model (Yu and

McMillan, 2004), but they have the important

advantage of projection continuity across an edge

shared by two adjacent C3RCs. In our algorithm

C3RCs are called upon to perform two basic

operations: 3D point projection and box-view

volume intersection.

5.1 C3RC Projection

The C3RC projection equation is cubic (Popescu et

al., 2006) so a C3RC can have up to 3 real

projections. We analyzed C3RC projection in detail

to understand if there are cases when more than one

of these real projections falls inside the triangular

image frame (base) of the C3RC. Such a multiple

projection occurs if two or more rays intersect, so a

natural approach is to solve the system of equations

that searches for a point on two rays. Intersecting

two rays yields a fourth order equation. Although

closed form solutions exist, it is difficult to decide

whether a solution is possible for rays inside the

triangular image frame, which has to be tested with

inequations on the barycentric coefficients of the

rays.

A simpler approach that confirmed the existence

of multiple projections is to describe the view

volume with a sweeping triangle that cuts equal

segments on the construction rays (Figure 4, left).

The first sweeping triangle is the C3RC base itself.

If a point Q projects inside the base of the C3RC at

barycentric coordinates a, b, and (1-a-b), then there

is a position T of the sweeping triangle that contains

Q at barycentric coordinates a, b, and (1-a-b). If Q is

to have two valid projections, there will be two

positions of the sweeping triangle that contain Q.

Figure 4, right shows two intersecting instances of

the sweeping triangle. Any point on the intersection

segment has at least two valid projections.

The sweeping triangle does not self-intersect for

divergent C3RCs, nor does it intersect for all

convergent-then-divergent C3RCs like the one seen

in Figure 4. We have established a method for

deciding whether a C3RC can have multiple

projections based on the observation that the

sweeping triangle cannot self-intersect while all 3

construction rays are on the same side of the

triangle’s plane. Initially all construction rays are on

the same side of the base. A construction ray

switches sidedness when it is contained in the plane

of the sweeping triangle.

The sweeping triangle positions where it contains

one of the construction rays are found by solving a

quadratic equation. If none of three equations has a

solution, the construction rays remain on the same

side of the sweeping triangle and no multiple

projections can occur. If one or more equations have

solutions, the view volume sub-region where

multiple projections can occur is defined by

sweeping parameter values in intervals where two

construction rays are on one side, and one if on the

opposite side of the sweeping triangle. For the

example shown in Figure 4, right, multiple-

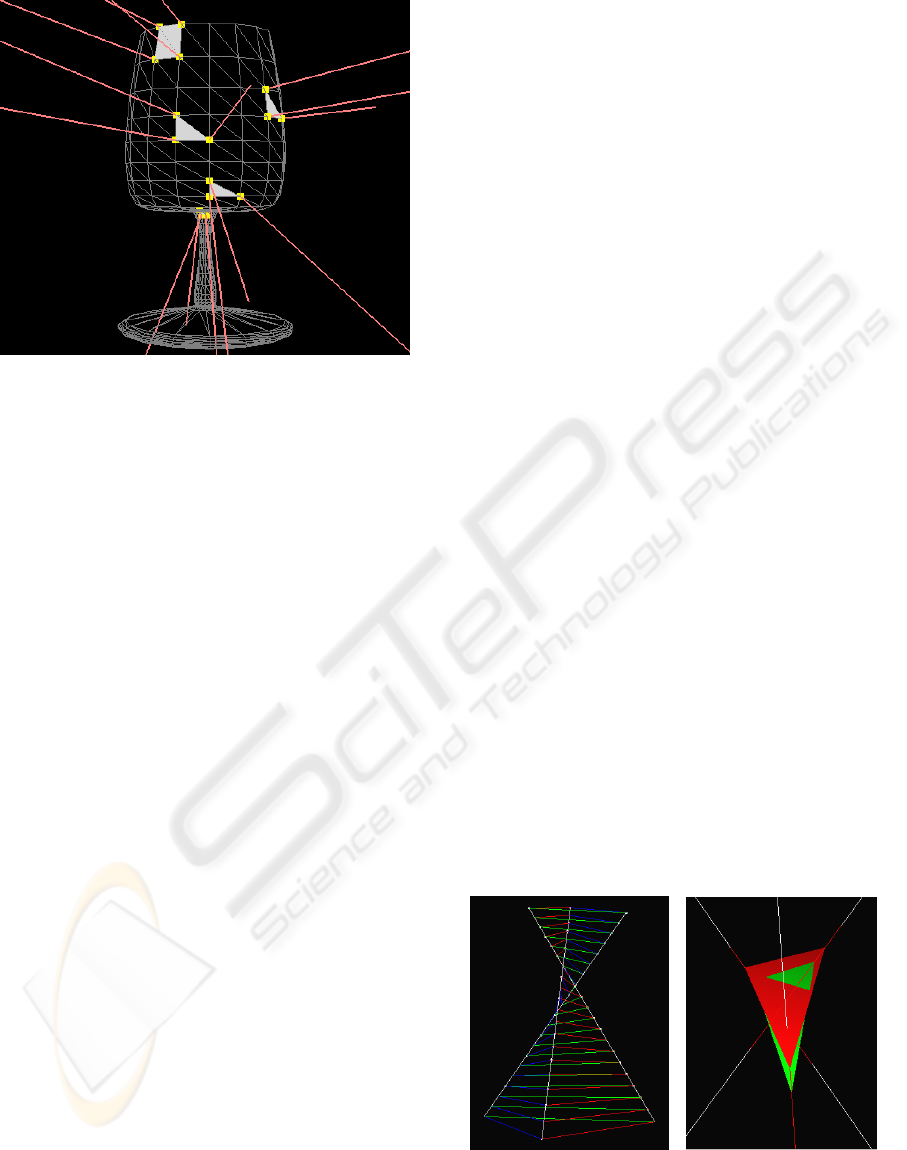
Figure 3: Visualization of sample C3RCs built for a glass

shaped reflector. The reflector triangles that define a C3RC

are shown in gray. The C3RC construction rays are shown

in red.

Figure 4: Sweeping triangle visualization of C3RC view

volume (left) and self-intersection of sweeping triangle

(right).

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

288

projections can occur when the sweeping triangle

intersects the construction rays inside the red

segments, which correspond to [0.98, 1.49].

5.2 Box-view Volume Intersection

During the “backward” phase the view volume of

each C3RC is intersected with the kd-tree to quickly

find the diffuse points inside visible to the C3RC.

For this one needs to decide whether a kd-tree node

(a box) does or does not intersect the view frustum.

A box clearly does not intersect a C3RC frustum if

both conditions below are met:

1. The box is not completely inside the frustum.

2. None of the 6 faces of the box intersects any

of the 3 side walls of the C3RC frustum.

Testing whether the first condition is satisfied is

simply done by testing whether an arbitrary box

corner does not have a valid projection.

To test for the second condition, we define the

side wall corresponding to base edge (v

, v

) of a

C3RC with the following parametric surface

)()(

)())(1(),(

121121

22111

dddvvv

dvdvS

−++−+=

−=

λαλα

where 0 <= α <=1, and d

and d

are the

directions of the rays through base vertices v

and v

is intersected with a planar face of the box with

corner point o

and normal n

by solving the

equation

0)(

=− nop

to find

11211

)(

nddnd

nvvnv

−+

−=

Substituting λ back into the equation of S

, the

intersection between the box face and the frustum

side wall is determined as a parametric curve p(α)

))((

)(

)()(

121

11211

121

ddd

nddnd

nvvnv

vvvp

−+

−

−+=

The curve p(α) is intersected with the four

segments defining the face frame, to determine

whether the side wall intersects the box plane inside

the face. Each intersection implies solving a

quadratic equation.

As always, the box–view frustum intersection is

over conservative for the purpose of occlusion

culling since the box is assumed to be completely

filled with payload geometry. The efficiency of the

occlusion culling is analyzed in the results section.

6 FEED-FORWARD PHASE

When a kd-tree leaf intersects the view volume of

the current C3RC, the points contained by the leaf

are projected with a GPU vertex program.

Unfortunately the GPU programming framework

does not support issuing multiple fragments per

vertex, so multiple projections are not supported.

The projected vertices are rasterized as square points

of fixed size (1 or 2 pixels). The reflected scene is

three dimensional and proper visibility sorting needs

to be enforced. When two points land on the same

pixel, the one closer to the reflector surface should

win. This is implemented by pushing back a

projected point along its desired view ray, similarly

to the visibility enforcing mechanism described for

sample-based cameras (Popescu et al., 2006). The

push back amount equals the distance from the

original diffuse point to the reflector surface, which

is given by the distance to the C3RC image plane.

The point-based approach was chosen to avoid

the difficulties of reflecting triangle meshes.

Consider a diffuse mesh of triangles. Each vertex

can have 0 or more projections. The multiple

projections can originate from the same C3RC, and,

more frequently, from different C3RCs. Before

rasterization can begin, one needs to examine the

projections of the 3 vertices of a given triangle in

order to form projected triangles. We have not found

a reliable way of grouping vertex projections in

projected triangles. Cases when the 3 vertices have a

different number of projections or when the

projections cannot be easily separated in clusters of

triples remain challenging. Moreover, even if the

grouping succeeds, conventional rasterization

assumes that the edges of the projected triangle are

straight, which holds only for small triangles or flat

reflectors. The approximation error has to be

controlled by subdividing the diffuse geometry,

which converges to the point-based approach.

Table 1: Kd-tree construction performance.

Scene

Points

x1,000

Constr.

time [ms]

Avg.

depth

Vertices

per leaf

Statue0 543 577 7.4 122

Dragon0 437 533 7.2 121

Bunny0 147 190 6.1 121

Dragon1 100 95 5.7 122

Bunny1 37 25 4.7 121

Dinosaur 10 6 3.4 123

A HYBRID BACKWARD-FORWARD METHOD FOR INTERACTIVE REFLECTIONS

289

A possible way for bypassing the difficulty of

forming reflected triangles is to work within one

C3RC at a time and to clip triangles that extend

outside the view volume of the C3RC. Since the side

walls of the C3RC are not planar, clipping a triangle

is expensive, and the resulting shape is complex,

possibly disconnected. Even a triangle completely

contained in the view volume of a C3RC can have a

complex projection if it crosses the sub-regions

where multiple projections occur.

7 RESULTS

We have tested the hybrid reflection rendering

method on several scenes with good results (Figures

1, 2, and 5, and accompanying video). The

background reflection is first rendered by

environment mapping and then the reflection of the

(synthetic) objects near the reflector is computed

with our method.

We have quantified performance for 6 test scenes

with variable diffuse geometry complexity. Images

of the 6 scenes are shown in row major order in

Figure 6. The same 4,000 triangle teapot is used as

reflector. All timing data reported in this paper was

measured on a 3GB 3.4GHz Pentium 4 Xeon PC

with a Quadro FX 3400 Nvidia graphics card.

The performance numbers of the kd-tree

construction are given Table 1. For small point sets

the kd-tree can be constructed on the fly. Rigid body

transformations of the diffuse object do not require

re-computing the kd-tree. The powerful eight-way

recursion makes the average tree depths and

numbers of points per leaf small.

The average hardware projection performance is

3.4 million vertices per second. The performance of

each of the two phases of reflection rendering is

given in Table 2 for each of the 6 test scenes. A

frame rate of 4 fps or better is obtained on all but the

two most complex diffuse scenes. Appropriate

parameters need to be chosen in the kd-tree

construction to balance the computation burden

between software culling and hardware projection. A

deep kd-tree and small leaf nodes accelerate

projection by increasing the ratio of valid projections

at the expense of slowing down view volume

culling. On the other hand a shallow tree and large

leafs reduce the culling effort at the expense of a

large number of unnecessary projections. The table

shows that for our system a good balance between

the two phases was obtained for a ratio of valid

projections of about 20%.

The performance of the method depends on the

complexity of the reflector in two ways. The number

of C3RCs equals the number of reflector triangles,

so the number of times the two rendering phases are

executed is linear in the number of reflector

triangles. The reflector shape complexity also

greatly influences performance. High curvatures

generate C3RCs with wide open view volumes,

Table 2: Reflection rendering performance.

Scene

Total

time [ms]

Culling

[ms]

Projection

[ms]

Valid proj.

[%]

Statue0 650 304 346 21

Dragon0 588 273 315 20

Bunny0 264 136 128 19

Dragon1 250 134 116 20

Bunny1 121 63 58 19%

Dinosaur 48 25 23 19%

Figure 5: Reflections of dragon and bunny rendered with

our method over an environment mapped background.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

290

which project a large number of points. For the

teapot for example, the handle, spout, and lid knob

project almost every point. Consequently most

points have on average 4 projections. Since the knob

is small in screen space, it should be rendered with

environment mapping.

8 CONCLUSIONS

Hybrid backward-forward reflection rendering

produces good results at interactive frame rates. The

versatility of points was leveraged to overcome

difficulties that arise in rendering reflected meshes.

This paper also furthers the understanding of

continuous 3-ray cameras which are important

infrastructure for applications beyond reflections.

Compared to ray-tracing, our technique is faster

if forward rendering of the geometry inside the

C3RC view volume is faster than ray tracing the

same geometry. This is the case if the reflector

triangle covers sufficient pixels in screen space. If

the reflector triangle covers only a few pixels, feed-

forward rendering does not pay off since the setup

cost is not amortized over enough pixels. Compared

to IBR techniques, our method has the advantage of

supporting highly specular surfaces and moving

objects, whereas IBR techniques can render scenes

with unknown geometry. Compared to reflected-

scene approximation techniques, our method is more

accurate, at the expense of performance.

Probably the best avenue for increasing

performance is to provide hardware support for the

C3RC. The projection is constant time, but the

constant is rather large, requiring solving a cubic.

Dedicated hardware could make C3RC projection as

efficient as conventional perspective projection.

Software view-frustum culling is equally expensive,

and we will investigate approaches for traversing the

kd-tree in the vertex program.

ACKNOWLEDGEMENTS

This work was supported by the United States

National Science Foundation through grants SCI-

0417458 and CCR-9617600.

REFERENCES

Bentley, J. L.: Data structures for range searching.

Computing Surveys, 11(4), December 1979.

Bjorke K.: Image-based lighting. GPU Gems, Fernando

R., (Ed.). NVidia, (2004), pp. 307–322.

Blinn J.F., Newell M.E.: Texture and Reflection in

Computer Generated Images. CACM 19:10, 542-547,

1976.

Cabral B.: Olano M., NEMEC P.: Reflection Space Image

Based Rendering. In Proc. of SIGG ‘99, pp.165-170.

Carr N., Hall J.D., Hart J.C. The Ray Engine, Graphics

Hardware (2002), pp. 1-10

Debevec P., Yu Y., Borshukov G.: 1998. Efficient view-

dependent image-based rendering with projective

texture-mapping. In Proc EGWR, 105–116.

Diefenbach P. J.: Pipeline Rendering: Interaction and

Realism Through Hardware-Based Multi-Pass

Rendering. PhD thesis, University of Pennsylvania,

(June 1996).

Glassner, A. An introduction to ray tracing. Academic

Press, 1989.

Greene, N. Environment mapping and other applications

of world projections. IEEE CG&A, 6:11, (1986).

Hall D.: The AR350.

Hakura Z.: Parameterized Environment Maps. In Proc. of

ACM I3D 2001 (2001), pp 203-208.

Hanrahan P., Mitchell D.: Illumination from curved

reflectors. In Proc. of SIGG ’92, ACM Press, pp. 283–

291.

Heidrich W.: Light Field Techniques for Reflections and

Refractions. EGRW 1999 (1999), pp.195-375.

Levoy M., Hanrahan P.: Light Field Rendering. Proc. of

SIGGRAPH 96 (1996), 31-42.

Lischinski D., Rappoport A.: Image-Based Rendering for

Non-Diffuse Synthetic Scenes. Eurographics

Rendering Workshop 1998 (1998), pp.301-314.

Figure 6: Scenes used to measure performance.

A HYBRID BACKWARD-FORWARD METHOD FOR INTERACTIVE REFLECTIONS

291

Miller G.: Lazy Decompression of Surface Light Fields

for Precomputed Global Illumination, Eurographics

Workshop on Rendering 1998 (1998).

Ofek E., Rappoport A.: Interactive reflections on curved

objects. In Proc. of SIGGRAPH ’98, ACM Press, 333-

342.

Parker, S.: Interactive ray tracing. ACM Symposium on

Interactive 3D Graphics (1999), 119–126.

Popescu, V., Dauble J., Mei, C., and Sacks, E.: An

Efficient Error-Bounded General Camera Model. In

Proc. of Third International Symposium on 3D Data

Processing, Visualization, and Transmission (2006).

Popescu, V., Sacks, E., and Mei C.: Sample-Based

cameras for feed forward reflection rendering. IEEE

Transactions on Visualization and Computer

Graphics, (2006), to appear.

Purcell T.J., Buck I., Mark W. Ray Tracing on

Programmable Graphics Hardware, In Proc. of SIGG

'02 (2002).

Reshetov A., Soupikov R., Hurley J.: Multi-Level Ray

Tracing Algorithm, In Proc. of SIGG 2005 (2005).

Shade J., Gortler S., He L., Szeliski R.: Layered Depth

Images, In Proc. of SIGG 98 (1998), 231-242.

Szirmay-Kalos L., Aszodi B., Lazanyi I., Premecz M.:

Approximate Ray-Tracing on the GPU with Distance

Impostors. Eurographics 2005 24, 3.

Wald I., Slussalek P., Benthin C.: Interactive distributed

ray tracing of highly complex models. In Rendering

Techniques 2001: 12th EGWR (2001), 277–288.

Wald I.: Interactive rendering with coherent ray tracing.

Computer Graphics Forum 20, 3 (2001), 153–164.

Weiskopf D., Schafhizel T., Ertl T. GPU-Based Nonlinear

Ray Tracing, In Proc. of EG '04 (2004).

Whitted T.: An improved illumination model for shaded

display. Comm. Of the ACM (1980), 23, 6, pp. 343-

349.

Wood D.N., Azuma D. I., Aldinger K.: Surface light fields

for 3D photography. In Proc. of SIGG ’00, pp. 287-

296.

Yu J., and McMillan, L.: General Linear Cameras In 8th

European Conference on Computer Vision (ECCV),

2004, Volume 2, 14-27.

Yu, J. and McMillan, L.: Real-time reflection mapping

with parallax. In Proceedings of ACM Symposium on

Interactive 3D Graphics and Games (I3D), 2005.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

292