EXTRACTING TERRAIN MORPHOLOGY

A New Algorithm and a Comparative Evaluation

Paola Magillo, Emanuele Danovaro, Leila De Floriani, Laura Papaleo and Maria Vitali

Department of Information and Computer Science, University of Genova, Via Dodecaneso, 35, 16146 Genova, Italy

Keywords:

Terrain models, Triangulated Irregular Networks, morphological structure.

Abstract:

We consider the problem of extracting morphology of a terrain represented as a Triangulated Irregular Network

(TIN). We propose a new algorithm and compare it with representative algorithms of the main approaches

existing in the literature to this problem.

1 INTRODUCTION

Extracting and representing morphological informa-

tion is a very relevant issue in order to develop auto-

matic tools for gaining and maintaining knowledge of

terrain models which are widely used in GIS applica-

tions, Virtual Reality and so on.

A terrain model is a scalar ﬁeld, i.e., a function

f (x,y) (usually called height function) deﬁned on a

domain D. Often, f is known only at a ﬁnite set of

sampled points and it is approximated through a dis-

crete digital model: a Regular Square Grid (RSG) if

the sampled points are regularly spaced, and a Tri-

angulated Irregular Network (TIN) if they are irreg-

ularly sampled. Both RSGs and TINs provide accu-

rate representations terrains, but they fail in capturing

the morphological structure deﬁned by critical points

(pits, peaks, passes), and integral lines, like (ridges,

valleys). On the contrary, a morphological terrain de-

scription is compact and supports a knowledge-based

approach to analyze, visualize and understand a ter-

rain dataset, as required, for instance, in visual data

mining applications.

In the last decades, there has been a lot of research

focusing on extracting critical features (points, lines

or regions) from images or terrain data described by

an RSG, or a TIN. More recent works in computa-

tional geometry concentrate on representing the mor-

phology of terrains through a decomposition of the

terrain surface into regions bounded by critical points

(minima, maxima, saddle points) and integral lines.

These techniques are rooted in Morse theory and try

to simulate the decomposition of a terrain induced by

Morse functions in the discrete case.

In this paper, we propose a new algorithm for ex-

tracting morphological information (in the form of the

stable and unstable Morse complexes) from a terrain

model described by a TIN, which is simple, requires

no ﬂoating point calculations, and can manage special

conﬁgurations such as ﬂat triangles and edges. We

also present a comprehensive study of analogous ex-

isting methods and propose a set of experiments in

order to evaluate our approach.

Recall that a TIN basically consists of a triangula-

tion Σ covering the ﬁeld domain D of the height func-

tion f , having its vertices at the sampled points. In

a triangulation, two nearby triangles can only touch

each other by sharing a vertex, or a common edge.

On each triangle t in Σ, function f is approximated as

a linear interpolant of the height values sampled at the

three vertices of t

In the remainder of this paper, Section 2 intro-

duces some basic background notions; Section 3 dis-

cusses related works; Section 4 presents our novel al-

gorithm; Section 5 introduces three representative al-

gorithms that we have implemented for comparison,

and Section 6 presents an experimental evaluation of

our novel algorithm compared to these three methods.

Finally, Section 7 draws some concluding remarks.

Note that RSGs can be reduced to TINs by triangulat-

ing each square into two triangles.

Magillo P., Danovaro E., De Floriani L., Papaleo L. and Vitali M. (2007).

EXTRACTING TERRAIN MORPHOLOGY - A New Algorithm and a Comparative Evaluation.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 13-20

DOI: 10.5220/0002076200130020

 SciTePress

2 BACKGROUND

Morse theory is a powerful tool to capture the topo-

logical structure of a scalar ﬁeld in the continuum

(Smale 1960). Let f be a C

real-valued function de-

ﬁned over a domain D ⊆ R

. A point p ∈ R

is called

a critical point of f if and only if the gradient of f

vanishes at p. The function f is a Morse function

if and only if the Hessian matrix H

f of the second

derivatives of f at a critical point p is non-singular

(its determinant is 6= 0): basically, if all its critical

points are non-degenerate. This implies that the criti-

cal points of a Morse function are isolated. The num-

ber of negative eigenvalues of H

f is called the index

of a critical point p. In 2D, a non-degenerate critical

point p of a Morse function f can be of three types:

a minimum (pit), a saddle, or a maximum (peak), if p

has index 0, 1 or 2, respectively. An integral line of

a function f is a maximal path which is everywhere

tangent to the gradient vector ﬁeld. It is emanating

from a critical point or from the boundary of D, and

it reaches another critical point or the boundary of D.

An integral line which connects a maximum to a sad-

dle, or a minimum to a saddle, is called a separatrix

line

Integral lines that converge to a maximum, a sad-

dle and a minimum form a 2-dimensional (region),

1-dimensional (line) and 0-dimensional (point) cell,

respectively, and they are called unstable manifolds.

Integral lines that originate from a minimum, a sad-

dle and a maximum form a 2-, 1- and 0-dimensional

cell, respectively, and they are called stable mani-

folds. The stable (unstable) manifolds are pair-wise

disjoint cells and form a complex, since the boundary

of every cell is the union of lower-dimensional cells.

They are called stable and unstable Morse complexes,

respectively. Figure 1(a) shows a decomposition of

the domain of a scalar ﬁeld into a stable Morse com-

plex.

A Morse function f is a Morse-Smale function

when the stable and the unstable manifolds intersect

only transversally. In two dimensions, this means that

the stable and unstable 1-manifolds (lines) cross when

they intersect, and the crossing points are saddles.

A Morse-Smale complex is the complex deﬁned

by the intersection of the stable and unstable Morse

complexes for a function f which is a Morse-Smale

function. The 1-skeleton of a Morse-Smale complex

consists of the critical points and the separatrix lines

joining them, and it is called a critical net (see Figure

In Geographic Information Systems (GISs), separa-

trix lines that connect minima to saddles are usually called

ravine, or valley lines, while those that connect saddles to

maxima are called ridge lines.

(a)

(b)

Maximum

Minimum

Saddle

Figure 1: (a) An example of a stable Morse complex (the 2-

manifolds correspond to the minima). (b) The Morse-Smale

complex. Its 1-skeleton is the critical net.

Figure 2: Edge labelled T-D is steeper than edge labelled

S-D. Numbers denote vertex heights.

1 (b)).

The surface network (Pfaltz 1976; Schneider and

Wood 2004) used in Geographic Information Systems

(GISs) for morphological terrain modeling, is essen-

tially the critical net.

3 RELATED WORK

Several algorithms have been proposed in the litera-

ture for decomposing the domain of a scalar ﬁeld f

(as a terrain model) into an approximation of a Morse

complex (or of a Morse-Smale complex). They either

ﬁt a C

or C

surface on a terrain model, or simulate a

Morse-Smale complex (a Morse complex) in the dis-

crete case. By assuming that no two adjacent vertices

in the TIN have the same height, they ensure that the

critical points are isolated, as in the Case of C

Morse

functions (Edelsbrunner et al. 2001).

A Morse (Morse-Smale) complex can also be de-

ﬁned using the concepts related to watershed tranform

(Meyer 1994; Vincent and Soille 1991; Roerdink and

Meijster 2000; Mangan and Whitaker 1999; Stoev

and Strasser 2000). The watershed transform in the

case provides a decomposition of a the domain of

a function f into open regions of inﬂuence associated

to the minima, called catchment basins. Catchment

basins can be described in terms of topographic dis-

tance (Meyer 1994). In the 2D case, if the function f

is a Morse function, the catchment basins of the min-

ima are essentially 2-manifolds of the stable Morse

complex. Through a change in the sign of the Morse

function f , the 2-manifolds (associated to the max-

ima) of the unstable Morse complex can be extracted.

In order to build a structural representation of a

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

given scalar ﬁeld f , all the existing methods extract

critical points of f as a ﬁrst step of the global proce-

dure. The most common approach to compute criti-

cal points examines, for each vertex p in the TIN, the

neighbors points (sharing with p and edge) and com-

putes the height difference between every point and

p. If all differences are positive (p is lower than its

neighbors), then p is a minumum. If all differences

are negative (p is higher than its neighbors), then p

is a maximum. If the number of sign changes of such

difference, while traversing p’s neighbors in ciclic or-

der, is two, then p is a regular, i.e., non-critical point.

If the number of sign changes is four, then p is a sad-

dle; if it is more than four, then p is a multiple saddle.

This technique is used by almost all the algorithms,

with the exception of (Bajaj and Shikore 1998).

Existing algorithms for extracting an approxima-

tion of a Morse (Morse-Smale) complex can be clas-

siﬁed according to: the input they consider (namely

RSG or TIN), the output they produce (namely an ap-

proximation of a Morse-Smale complex or of a Morse

complex) and the algorithmic technique they choose.

Here, we have classiﬁed them into boundary-based or

region-based techniques (Comic et al. 2005).

Boundary-based techniques basically extract an

approximation of the critical net, by computing the

critical points and then tracing the integral lines, start-

ing from saddle points (Bajaj et al. 1998; Schnei-

der 2005; Takahashi et al. 1995; Edelsbrunner et

al. 2001; Bajaj and Shikore 1998; Bremer et al.

2003; Pascucci 2004). Region-based techniques ex-

tract a discrete approximation of the stable and unsta-

ble Morse complexes, by starting from minima and

maxima and letting a region grow until a given con-

dition is reached (Danovaro et al. 2003a; Danovaro

et al. 2003b; Meyer 1994; Vincent and Soille 1991;

Mangan and Whitaker 1999). We included watershed

algorithms in the latter class since they are region-

based in nature.

In Section 5 we present our implementations of

some representative algorithms of the above tech-

niques. All algorithms, with the exception of the

watershed approach, require that the three vertices

of a triangle have distinct heights. This is gener-

ally achieved, when necessary, by perturbation of the

height values.

4 THE STD ALGORITHM

In this section we present our novel algorithm, that

we called STD, for extracting the 2-manifolds (asso-

ciated with the minima) of a stable Morse complex for

a (Morse) function f deﬁned on a TIN. The algorithm

is region-based in nature since it starts from the min-

ima and lets the 2-manifolds of the Morse complex

grow as long as it is possible.

We ﬁrst describe the algorithm under the assump-

tion that no two vertices of the terrain have the same

height. Successively, we relax this assumption and

show how to deal with ﬂat triangles, and triangles

having one ﬂat edge.

4.1 Basic Version of the Algorithm

The STD algorithm performs three main steps:

1. Classify the vertices of each triangle t in the TIN,

based on their heights.

2. Extract the minima of the function in the TIN.

3. For each minimum p, construct the stable 2-

manifold by iteratively adding triangles to it.

Vertex classiﬁcation and Extraction of local min-

ima. For each triangle t in the TIN, the highest,

middle, and lowest vertex are labeled as Source (S),

Through (T), and Drain (D), respectively.

By this STD conﬁguration of the vertices we ba-

sically simulate the gradient direction of t in the dis-

crete case. Note that this labelling does not assume

any kind of interpolation (linear or higher-order) on

triangles or edges of the mesh. Edge labelled S-D is

not necessarily the edge of steepest descent. In Figure

2 the steepest descent is at edge labelled T-D.

The local minima identiﬁcation is very simple:

they are found as those vertices labeled D in all their

incident triangles.

Construction of the stable 2-manifolds. For each

minimum p, the stable 2-manifold γ

associated with

p is initialized with all triangles of the TIN which are

incident in p. Successively, an iterative phase starts

in which, at each step, the algorithm decides if a tri-

angle t, externally adjacent to one edge e of the cur-

rent perimeter of γ

, can be added to γ

. The ratio-

nale for this decision takes the following issues into

account: (i) the choice must reﬂect the intuition that

water ﬂows from a higher to a lower height, (ii) the

choice must be deterministic, i.e., a triangle t cannot

be included into different 2-manifolds, depending on

the order in which minima are processed.

The algorithm maintains the invariant that, if a tri-

angle t has been included into γ

, then the edge of t

labelled T-D is not on the boundary of γ

4.2 Inclusion of a Triangle

Let e be an edge of the current perimeter of γ

, and

t be the triangle externally adjacent to e. The deci-

sion whether to include t into γ

or not, is based on

EXTRACTING TERRAIN MORPHOLOGY - A New Algorithm and a Comparative Evaluation

(a) (b)

Figure 3: Case 1 (a) and Case 2 (b). Arrows denote water

ﬂow. Green triangles are included.

the STD conﬁguration of its vertices. There are three

possible cases.

Case 1. If the vertex v of t opposite to e is labelled D

in t, then we do not include t into γ

. See Figure 3 (a).

This is according to the intuition that water cannot

exit t through e, since it naturally ﬂows towards v.

Triangle t will be included when we will reach it from

another edge, and Case 2 or 3 will hold.

Case 2. If the vertex v of t opposite to e is labelled

S in t, then we include t into γ

. See Figure 3 (b). In-

tuitively, water tends to ﬂow across t and reach vertex

, endpoint of e, which is labelled D in t. The ques-

tion is whether it will exit t through e (in that case

t belongs to γ

) or through the edge of t labelled S-

D. Now, we explain why we have decided that water

passes through edge e.

Let t

be the triangle belonging to γ

and adjacent

to t along e, and let v

be the vertex of t

opposite to e.

Note that, for the invariant, e cannot be labelled T-D

in t

(equivalently, v

cannot be labelled S).

If e is labelled S-T in t

, then water enters t

through e, therefore it must exit from t through e.

If e is labelled S-D in t

, then water exits t

through its edge e

labelled T-D (it cannot exit

through the other edge, since it is labelled S-T, and

it must exit from one edge different from e otherwise

would not have been included in γ

). Therefore wa-

ter that ﬂows across t and reaches vertex v (which is

labelled D in both t and t

) turns around v

, enters t

and ﬁnally exits t

through e

Note that the invariant is maintained: edge e (la-

belled T-D in the newly included triangle t) is inside

the updated 2-manifold γ

Case 3. If the vertex v of t opposite to e is labelled

T in t, then the situation is more complex. Certainly,

water ﬂows to vertex v

, endpoint of e, which is la-

belled D in t. Then, will it exit from t into γ

through

edge e, or will it exit t through its edge e

labelled T-D,

towards the 2-manifold existing on the other side?

Starting from t, we explore the maximal fan of tri-

angles having their lowest vertex in v

(i.e., v

is la-

belled D in all such triangles). Let w be the vertex

(a) (b) (c)

Figure 4: (a) Case 3 with non-empty set of included trian-

gles; green triangles are included. (b) Case 3 with empty

the set of included triangles. (c) Inclusion of the remaining

triangles of the fan by applying Case 2 from edge e

of maximum height among the vertices of such trian-

gles. The part of the fan starting from t and going up

to edge v

w is included into γ

. See Figure 4 (a). The

other part of the fan will be later included into the 2-

manifold existing on the other side. Note that, if w is

the same as the vertex labelled S in t, then no triangle

is included. See Figure 4 (b).

The invariant is maintained since the edges re-

maining on the boundary of the updated 2-manifold

are v

w, and edges opposite to v

: none of them is

labelled T-D. In fact, edges opposite to v

are labelled

S-T in the just included triangles, and edge v

w is la-

belled S-D in both adjacent triangles.

Note that the management of Case 3 does not in-

terfere with Case 2. In fact, the edge e

marking the

other side of the fan may be labelled T-D in its ad-

jacent triangle t

belonging to the fan. In this case,

when reached from e

, t

will be included into the 2-

manifold γ

existing on the other side of e

. The trian-

gle adjacent to t

along the other edge of t

incident in

may be in the same situation (and thus be included

in γ

as well), and so on. Thus, a whole fan of tri-

angles, starting from t

, is included into γ

. But this

fan must end at edge w, because the opposite vertex

to v

w is labelled T in the next triangle. Thus, there is

no interference between Case 3 applied from edge e,

and Case 2 repeatedly applied starting from edge e

See Figure 4 (c).

4.3 Time Complexity

It can be easily shown that every triangle t of the TIN

is examined at most three times, one from each edge,

before being included into some 2-manifold. Thus,

the worst-case time complexity of our algorithm is

O(n) where n is the number of TIN vertices. The

only non-trivial part in this statement is showing that,

in Case 3, a triangle can be in a traversed fan, with-

out being included, at most once during the whole al-

gorithm. The triangles of the fan, which are not in-

cluded, are those located beyond edge v

w. The same

fan may be traversed from the opposite side, while

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

growing another 2-manifold γ

. Since we will be tra-

versing the same fan in the opposite way, in that situ-

ation exactly those triangles, that were not previously

included, will be found before edge v

w, and will be

included into γ

4.4 Management of Special Cases

Now, we explain how the STD algorithm deals with

ﬂat triangles, and triangles with a ﬂat edge.

In a preprocessing step, we ﬁnd edge-connected

areas of ﬂat triangles, and vertex-connected networks

of ﬂat edges that are not edge- or vertex-incident into

a ﬂat triangle. Such areas / networks are candidate to

act as 1- or 2-dimensional local minima. Let h be the

height of a ﬂat area or network. Let h

be the min-

imum height of the third vertices of triangles exter-

nally adjacent to the perimeter of the ﬂat area, or in-

cident into edges of the network. If h

> h then the

ﬂat area / network is treated as a local minimum: its

2-manifold is initialized with all the triangles of the

ﬂat area, or with all triangles incident in the ﬂat net-

work, and it is expanded in the same way as other

2-manifolds.

A ﬂat area that is not a local minimum (i.e., h

< h)

is assigned to the 2-manifold containing the triangle

, externally adjacent to the ﬂat area, whose third ver-

tex has height h

. If t

is not unique, then we choose

the 2-manifold corresponding to the lowest local min-

imum (if unique), or arbitrarily (otherwise).

During the algorithm, triangles with a ﬂat edge

may be examined to test whether they can be included

into a growing 2-manifold. For such purpose, Cases

1,2, and 3 introduce some exceptions when triangle t

has a ﬂat edge.

An exception may arise in Case 1, when the oppo-

site vertex v, labelled D, is endpoint of the ﬂat edge

of t. In this case, we consider triangle t

which is ad-

jacent to t along its ﬂat edge. If edge e

is higher than

the third vertex of t

, we do not include t (no excep-

tion). If edge e

is lower than the third vertex of t

then this is an exception: we construct the fan of tri-

angles incident into the vertex of t which is labelled

D, and proceed in the same way as in Case 3.

Another exception arises in Case 2, when the op-

posite vertex v, labelled S, is endpoint of the ﬂat edge

of t. In this case, the two non-ﬂat edges of t, e and

, are in the same situation. We must decide whether

to include t into γ

from e, or to include t into the 2-

manifold that will reach t from edge e

. We construct

the fan of triangles incident into the vertex of t which

is labelled D, and proceed as in Case 3.

In Case 3, the constructed fan cannot include ﬂat

triangles, and cannot include triangles with a ﬂat

edge, when the ﬂat edge belongs to a local minimum

network. If we ﬁnd one of these cases, then we stop

extending the fan.

Case 3 takes the edge v

w, connecting the cen-

ter v

of the fan with its upper point w, as the edge

where to split the fan and assign its triangles to the 2-

manifolds existing on the two sides of the fan. Now,

vertex w of maximum height may not be unique. Let

, w

, ... w

(M > 1) be the vertices having the max-

imum height, sorted in counterclockwise order along

the fan. We split the fan at edge v

where i is the

integer result of division M/2.

5 REPRESENTATIVE

MORPHOLOGY ALGORITHMS

We have implemented a number of algorithms that we

have chosen as representative of the approaches exist-

ing in the literature (Section 3).

5.1 A Boundary-based Algorithm

Our implementation of a boundary-based approach,

inspired by (Edelsbrunner et al. 2001; Takahashi et

al. 1995), extracts the Morse-Smale complex from a

TIN by computing the critical net, in two basic steps:

1. Extract the critical points and unfold multiple

saddles.

2. Compute the 1-cells of the complex by starting

from the saddle points, and tracing two paths of

steepest descent and two paths of steepest ascent,

which stop at minima and maxima, respectively.

Starting from each (simple) saddle p, the algo-

rithm computes the four lines belonging to the crit-

ical net which are incident in p. At each step, the

path is extended by adding the edge corresponding to

the maximum positive [negative] slope, until a maxi-

mum [minimum] is found. In the implementation we

present in this paper we refer only to the stable Morse

complex: for each saddle we trace two lines which

follow the maximum positive slope and stop when

two maxima are found.

5.2 A Region-based Algorithm

We have presented in (Danovaro et al. 2003a) an al-

gorithm for computing both the stable and unstable

Morse complexes for a TIN. The algorithm can be

sketched into two main steps:

1. Extract minima and maxima.

EXTRACTING TERRAIN MORPHOLOGY - A New Algorithm and a Comparative Evaluation

2. Compute the stable (unstable) Morse complex by

applying a region-growing procedure. This proce-

dure adds triangles to a 2-manifold iteratively.

For extracting the stable Morse complex, the algo-

rithm computes the gradient for each triangle t in M,

and the angles between the gradient and the normal

vector at each edge of t (pointing outwards from the

triangle). The edges of t corresponding to the largest

and to the smallest angle are marked as exit and en-

trance, respectively.

A 2-manifold γ

of the stable complex is initial-

ized with the triangles incident in a local minimum p.

At a generic step, γ

is extended by adding a new tri-

angle t sharing an edge e with γ

, provided that e is an

entrance for t and an exit for the triangle t

in γ

shar-

ing edge e with t. The unstable complex is computed

in a completely symmetric way.

5.3 A Watershed Algorithm

We have implemented the watershed algorithm based

on simulated immersion (Vincent and Soille 1991).

Our implementation is applicable to TINs with ﬂat

edges and/or ﬂat triangles and it consists of mainly

three macro-steps:

1. Sort the vertices in increasing order with respect

to the height value.

2. Perform the ﬂooding step level by level, starting

from the minima: this labels every vertex as be-

longing to a 2-manifold associated to a minimum.

3. Assign triangles to basins based on the labels of

their vertices.

The ﬂooding step assigns a distinct label to each

minimum m and to the vertices of its associated 2-

manifold γ

. Those vertices, where two 2-manifolds

meet are instead labeled as watershed vertices. At

each iteration, a height value h (initially, the mini-

mum height) is considered. All vertices with the same

height h are ﬁrst given a neutral label. Then those ver-

tices whose neighbors have been labeled during the

previous iteration are processed in order to assign the

label of a 2-manifold γ

to them.

To assign the label to a vertex p, we examine

the neighbor vertices of p. If they all belong to the

same 2-manifold γ

or are watershed points, then p

is marked as belonging to γ

. If they belong to two

or more different 2-manifolds, then p is marked as a

watershed point. The same operations is recursively

repeated on the neighbors points of the just labeled

vertices which have a neutral label (i.e., height = h).

Vertices at height h that are not connected to any

previously processed vertex still have the neutral la-

EGGS (6561 vertices) MARCY (1000 vertices)

Figure 5: Two of the test TINs.

bel. Such vertices belong to a set of new minima at

level h, and get a new label.

Finally, we label each triangle t. If all the vertices

of t, that are not watershed points, belong to the same

2-manifold γ

, then we assign the triangle to γ

. If

two vertices belong to different 2-manifolds, then t is

assigned to the 2-manifold related to the vertex with

the lowest height.

6 EXPERIMENTS

The goal of this section is to measure the quality of the

results of the STD algorithm proposed in this paper,

as well as evaluating the degree of uncertainty in mor-

phology computation, i.e., to which extent the current

algorithms are able to provide consistent results. We

perform different experimental comparisons on both

real and synthetic datasets by using our STD algo-

rithm, the boundary-based (BND), the region-based

(REG), and the watershed (WTS) algorithm described

in Section 5.

Algorithm STD is of course very different from

BND; STD and WTS have in common the idea of

growing 2-manifolds from local minima; REG is sim-

ilar in approach, but (i) uses the gradient, and (ii) it

builds a 2-manifold in pieces which are then glued to-

gether, while STD builds every 2-manifold directly,

thanks to the mechanism of fans (Case 3).

We show results using two different terrains: (i)

EGGS, a synthetic terrain built by sampling a func-

tion which is a combination of two planes and 64

gaussian surfaces, and (ii) MARCY representing part

of a real terrain model provided with the US Geolog-

ical Survey in which heights have been perturbed in

order to remove ﬂat edges.

We have three TINs for EGGS, corresponding

to different sampling resolutions (6,561, 25,921, and

103,041 vertices), and three TINs for MARCY, corre-

sponding to approximations of the terrain at different

resolutions (1,000, 5,000 and 10,000 vertices). See

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

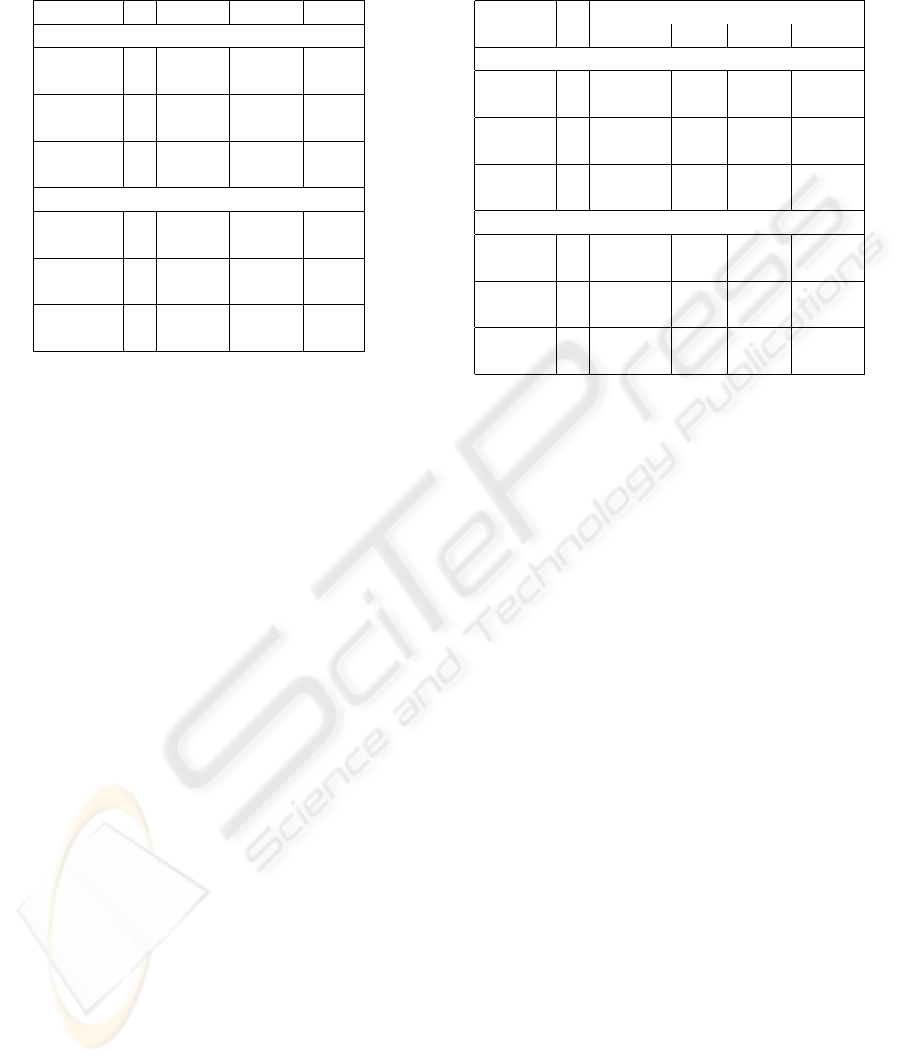
Table 1: Triangles (t) and percentage of terrain area (a) as-

signed to a different 2-manifold in the new STD algorithm

and in one of the other three methods.

# triang. BND REG WTS

EGGS

12,800 t 398 669 71

a 3.11 5.23 0.55

51,200 t 1934 2,721 62

a 3.78 5.31 0.12

204,800 t 14,828 14,488 112

a 7.24 7.07 0.55

MARCY

1,910 t 107 98 39

a 3.89 2.95 1.64

9,788 t 554 690 151

a 4.73 6.10 1.31

19,602 t 1,802 2,066 356

a 9.20 10.54 1.82

Figure 5. Some images of the computed stable Morse

complexes are in Figures 7 and 6.

Table 1 evaluates the difference in the results be-

tween our new STD algorithm and the other three.

This also provides a measure of the uncertainty of re-

sults. In general, the STD algorithm tends to be closer

to the watershed method.

Table 2 reports the quantity of TIN surface whose

classiﬁcation results uncertain (i.e., assigned to the 2-

manifold of different minima in different algorithms).

The various algorithms may disagree in their results

up to an extent between 0.5% and 10.5% of the total

TIN surface.

It may be surprising that algorithms differ so much

in their results: up to 9% of the terrain area may be as-

signed to four different minima by the four considered

approaches. It is also difﬁcult to judge which one is

more correct, because a ground thruth is only avail-

able for C

functions, and not for TINs. Indeed, all

existing methods only approximate Morse (or Morse-

Smale) theory in the discrete case, through simpliﬁ-

cations, conventions, and heuristics.

7 CONCLUDING REMARKS

We have proposed a new algorithm for computing

the stable (unstable) Morse complex for a TIN ter-

rain model. We performed experiments on both real

and synthetic datasets in order to demonstrate the be-

havior of the STD algorithm with respect to other al-

gorithms, as well as the intrinsic uncertainty of stable

manifolds computation at this stage of research. We

showed that our STD algorithm behaves quite well

Table 2: Triangles (t) and percentage of terrain area (a) as-

signed to a unique 2-manifold, or to 2, 3 and 4 different

2-manifolds, by the four algorithms.

# # of different 2-manifolds

triang. 1 2 3 4

EGGS

12,800 t 11,963 42 397 398

a 93.46 0.33 3.10 3.11

51,200 t 48,221 42 1,003 1,934

a 94.18 0.08 1.96 3.78

204,800 t 184,608 48 5,316 14,828

a 90.14 0.02 2.60 7.24

MARCY

1,910 t 1,744 13 46 107

a 94.18 0.64 1.31 3.87

9,788 t 8,835 56 343 554

a 90.26 0.57 3.50 5.66

19,602 t 17,114 149 537 1,802

a 87.31 0.76 2.74 9.19

for all the test datasets and that it provides intuitively

good results. Moreover, our algorithm is very sim-

ple, and requires no ﬂoating-point calculations since

it uses only numerical comparisons.

Morphology algorithms that can be extended to

higher dimensions have a special interest from the sci-

entiﬁc community. Our STD algorithm is as simple as

the boundary-based approach and, unlike it, seem to

be more easily extensible to higher dimensions. For

instance, in 3D we label the four vertices of each tetra-

hedron and have four cases to be managed.

Finally, (Danovaro et al. 2003a) present a

morphology-based multi-resolution terrain model, to

encode different levels of approximation of a Morse-

Smale complex. We plan to use the STD algorithm in

this context.

ACKNOWLEDGEMENTS

This work has been partially supported by the Eu-

ropean Network of Excellence AIM@SHAPE (con-

tract n. 506766), by the National Science Foundation

(grant CCF-0541032), by the MIUR-FIRB project

SHALOM (contract n. RBIN04HWR8) and by the

MIUR-PRIN project on “Multi-resolution modeling

of scalar ﬁelds and digital shapes”.

EXTRACTING TERRAIN MORPHOLOGY - A New Algorithm and a Comparative Evaluation

STD BND REG WTS

Figure 6: The boundary of the stable Morse complex computed by the four algorithms on the EGGS. terrain (6561 vertices).

STD BND REG WTS

Figure 7: The boundary of the stable Morse complex computed by the four algorithms on the MARCY. terrain (1000 vertices).

REFERENCES

C. L. Bajaj, V. Pascucci, and D. R. Shikore. Visualization

of scalar topology for structural enhancement. In Pro-

ceedings IEEE Visualization’98, pages 51–58. IEEE

Computer Society, 1998.

C. L. Bajaj and D. R. Shikore. Topology preserving data

simpliﬁcation with error bounds. Computers and

Graphics, 22(1):3–12, 1998.

P.-T. Bremer, H. Edelsbrunner, B. Hamann, and V. Pascucci.

A multi-resolution data structure for two-dimensional

Morse functions. In Proceedings IEEE Visualization

2003, pages 139–146. IEEE Computer Society, 2003.

L. Comic, L. De Floriani, and L. Papaleo. Morse-Smale de-

composition for modeling terrain knowledge. In Spa-

tial Information Theory: International Conference,

volume 3693 of Lecture Notes in Computer Science,

pages 426–444, 2005.

E. Danovaro, L. De Floriani, P. Magillo, M. M. Mesmoudi,

and E. Puppo. Morphology-driven simpliﬁcation and

multi-resolution modeling of terrains. In Proceed-

ings ACM-GIS 2003 - The 11th International Sym-

posium on Advances in Geographic Information Sys-

tems, pages 63–70. ACM Press, 2003.

E. Danovaro, L. De Floriani, and M. M. Mesmoudi. Topo-

logical analysis and characterization of discrete scalar

ﬁelds. In Theoretical Foundations of Computer Vision,

Geometry, Morphology, and Computational Imaging,

volume 2616 of Lecture Notes on Computer Science,

pages 386–402. Springer Verlag, 2003.

H. Edelsbrunner, J. Harer, and A. Zomorodian. Hierarchical

Morse complexes for piecewise linear 2-manifolds. In

Proceedings 17th ACM Symposium on Computational

Geometry, pages 70–79. ACM Press, 2001.

A. Mangan and R. Whitaker. Partitioning 3D surface

meshes using watershed segmentation. IEEE Trans-

action on Visualization and Computer Graphics,

5(4):308–321, 1999.

F. Meyer. Topographic distance and watershed lines. Signal

Processing, 38:113–125, 1994.

V. Pascucci. Topology diagrams of scalar ﬁelds in scien-

tiﬁc visualization. In Topological Data Structures for

Surfaces, pages 121–129. John Wiley and Sons Ltd,

2004.

J. L. Pfaltz. Surface networks. Geographical Analysis,

8:77–93, 1976.

J. Roerdink and A. Meijster. The watershed transform:

deﬁnitions, algorithms, and parallelization strategies.

Fundamenta Informaticae, 41:187–228, 2000.

B. Schneider. Extraction of hierarchical surface networks

from bilinear surface patches. Geographical Analysis,

37:244–263, 2005.

B. Schneider and J. Wood. Construction of metric surface

networks from raster-based DEMs. In Topological

Data Structures for Surfaces, pages 53–70. John Wi-

ley and Sons Ltd, 2004.

S. Smale, Morse Inequalities for a Dynamical System, Bul-

letin of American Mathematical Society, 66: 43–49,

1960.

S. L. Stoev and W. Strasser. Extracting regions of interest

applying a local watershed transformation. In Pro-

ceedings IEEE Visualization’00, pages 21–28. IEEE

Computer Society, 2000.

S. Takahashi, T. Ikeda, T. L. Kunii, and M. Ueda. Al-

gorithms for extracting correct critical points and

constructing topological graphs from discrete geo-

graphic elevation data. Computer Graphics Forum,

14(3):181–192, 1995.

L. Vincent and P. Soille. Watershed in digital spaces: an

efﬁcient algorithm based on immersion simulation.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 13(6):583–598, 1991.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications