
SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE
SIMPLIFICATION
Sumanta Guha, Paul Janecek and Nguyen Duc Cong Song
CSIM Program, Asian Institute of Technology, P.O. Box 4, Klong Luang, Pathumthani 12120, Thailand
Keywords:
Curvature, curve simplification, Douglas-Peucker, level of detail, polygonal curve, polyline, simplification
algorithm, SimpliPoly.
Abstract:
A curvature-based algorithm to simplify a polygonal curve is described, together with its implementation. The
so-called SimpliPoly algorithm uses B´ezier curves to approximate pieces of the input curve, and assign curva-
ture estimates to vertices of the input polyline from curvature values computed for the B´ezier approximations.
The implementation of SimpliPoly is interactive and available freely on-line. Empirical comparisons indicate
that SimpliPoly performs as well as the widely-used Douglas-Peucker algorithm in most situations, and sig-
nificantly better, because it is curvature-driven, in applications where it is necessary to preserve local features
of the curve.
1 INTRODUCTION
LOD (Level of Detail) management is becoming an
increasingly important issue in interactive computer
graphics and visualization because of performance
requirements in rendering and transferring complex
images. Objects are often stored in multiple LODs,
or resolutions, and the appropriate LOD chosen for
a subsequent application. A variety of techniques
have been developed for the purpose of computing
LODs, typically beginning with the original object,
and then increasingly coarse, a process called simpli-
fication. See (Heckbert and Garland, 1995; Luebke
et al., 2003) for surveys. Most of the current litera-
ture in computergraphics and available softwaredeals
with the simplification of surfaces in 3D.
We focus in this paper on a somewhat restricted
LOD problem, that of simplifying a plane polygonal
curve, also called polyline. Nevertheless, this prob-
lem is of interest in several application areas as well,
ranging from sketch simplification to map simplifica-
tion in GIS (Geographical Information Systems). Fig-
ure 1 gives an example of the utility of polyline sim-
plification: the figure on the right is about a sixth as
complex as the original one the left, yet is likely faith-
ful enough to be adequate for many purposes, while
the one in the middle at much less than half the com-
plexity is almost indistinguishable from the original.
The main contribution of this paper is an algo-
rithm and its derivative software package – together
called SimpliPoly – that can be used to interactively
simplify a polyline. SimpliPoly makes a novel ap-
plication of the notion of curvature from differential
geometry to the simplification problem. In particular,
our approach is to estimate the curvature of a polyline
at its vertices.
A polylineC, except for the trivial situation where
all its vertices lie on a straight line, is not smooth.
Accordingly, differential geometric measures of cur-
vature cannot be applied directly to C itself. Our
method is, instead, to first approximate pieces of C
with B´ezier curves, and then “lift” curvature values
from points of the approximations to vertices of C.
Subsequently, vertices ofC with low curvature are re-
moved on the premise that they lie on “straightish”
parts of C.
The technique is motivated mostly by heuristic ar-
guments, our goal first and foremost being simple and
practical software. We do not prove results about the
quality of the simplification. Unfortunately, it seems
difficult to do so, giventhe nature of the heuristics em-
ployed; nevertheless, they are all fairly intuitive and
166
Guha S., Janecek P. and Duc Cong Song N. (2007).
SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 166-171
DOI: 10.5220/0002072801660171
Copyright
c
SciTePress

(a) (b) (c)
Figure 1: Multiple LODs: (a) 150 vertices (b) 60 vertices (c) 26 vertices.
justified by the context. Moreover, the SimpliPoly
software package is designed to be used interactively,
so that the user monitors the output until she per-
ceives the simplification to be satisfactory, rather than
depending upon an a priori guarantee of its quality.
Our results – which the reader is invited to verify
using the on-line Java version (SimpliPoly, 2006) –
indicate that SimpliPoly indeed works well in prac-
tice, producing faithful simplifications over a range of
user-controlled quality parameters. Its interface too is
easy-to-use making SimpliPoly an attractive option in
various application domains.
Currently, the polyline simplification algorithm
used most commonly in practice is the Douglas-
Peucker algorithm (Douglas and Peucker, 1973),
which is a recursive algorithm based on reducing a
distance error between an input polyline and its sim-
plification. Douglas-Peucker is easily implemented,
fairly efficient, and generally produces good-quality
output – all reasons for its popularity. However,
Douglas-Peucker is purely “distance-error driven”; it
does not “recognize” local features, e.g., a sharp turn,
a protrusion, etc., and, therefore, makes no attempt to
preserve such features as it simplifies. SimpliPoly, on
the other hand, being “curvature-driven”, does recog-
nize features and tends to keep them. At the same
time, because stretches of a polyline with low dis-
tance error from a simplification tend in practice to
be of low curvature values as well, the ability of Sim-
pliPoly to simplify such stretches appears to be com-
petitive with Douglas-Peucker.
At present, the theoretically best algorithms for
polyline curve simplification are from Agarwal et al.
(Agarwal et al., 2002), who obtain provably near-
optimal simplifications within specified distance er-
ror bounds. However, their algorithms are complex
and there seems to be no practical implementation yet.
Moreover, the only curvature-based simplification al-
gorithms that we are aware of are due to Kim et al.
(Kim et al., 2002) and references therein, all of which
deal with surfaces rather than curves. Again, these
algorithms are all fairly complex and no code seems
available.
The next four sections discuss successively the
SimpliPoly algorithm in detail, its analysis, applica-
tions, and, finally, conclusions.
2 ALGORITHM
Let C be a polyline joining the n + 1 vertices
v
0
,v
1
,...,v
n
, where n ≥ 5. SimpliPoly computes the
B´ezier approximationof a “sliding window”of length
five vertices of C as follows. First, it determines the
B´ezier curve c
0
(u),0 ≤ u ≤ 1, of order five with ver-
tices v
0
,v
1
,...,v
4
as control points, then the curve
c
1
(u) with v
1
,v
2
,...,v
5
, as control points, and so on,
till the curve c
n−4
(u) with v
n−4
,v
n−3
,...,v
n
as control
points.
The formula for c
i
(u) is
c
i
(u) =
i+4
∑
r=i
B
r,4
(u)v
i+r
, 0 ≤ i ≤ n− 4
where
B
r,4
(u) =
4
r
(1− u)
4−r
u
r
, 0 ≤ r ≤ 4
are the blending functions, which happen to be the
Bernstein polynomialsof degree four in this case. See
Farin (Farin, 2001) for a discussion of B´ezier theory
in general.
Note that there is no particular reason to choose
order five for the B´ezier approximation, other than
it seems to span a reasonable number of vertices of
C, and yet is not large enough to be computationally
problematic.
Figure 2 shows the first two approximating curves
for a polyline: c
0
(u) (solid) and c
1
(u) (dashed).
Next, for each B´ezier curve c
i
(u), 0 ≤ i ≤ n − 4,
SimpliPoly determines the curvature at the three inte-
rior points c
i
(0.25), c
i
(0.5) and c
i
(0.75), and “lifts”
them to the control vertices v
i+1
, v
i+2
and v
i+3
, re-
spectively. This is done as the blending function cor-
responding to each of these three vertices has max-
imum value at the point of c
i
(u) whose curvature is
SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION
167
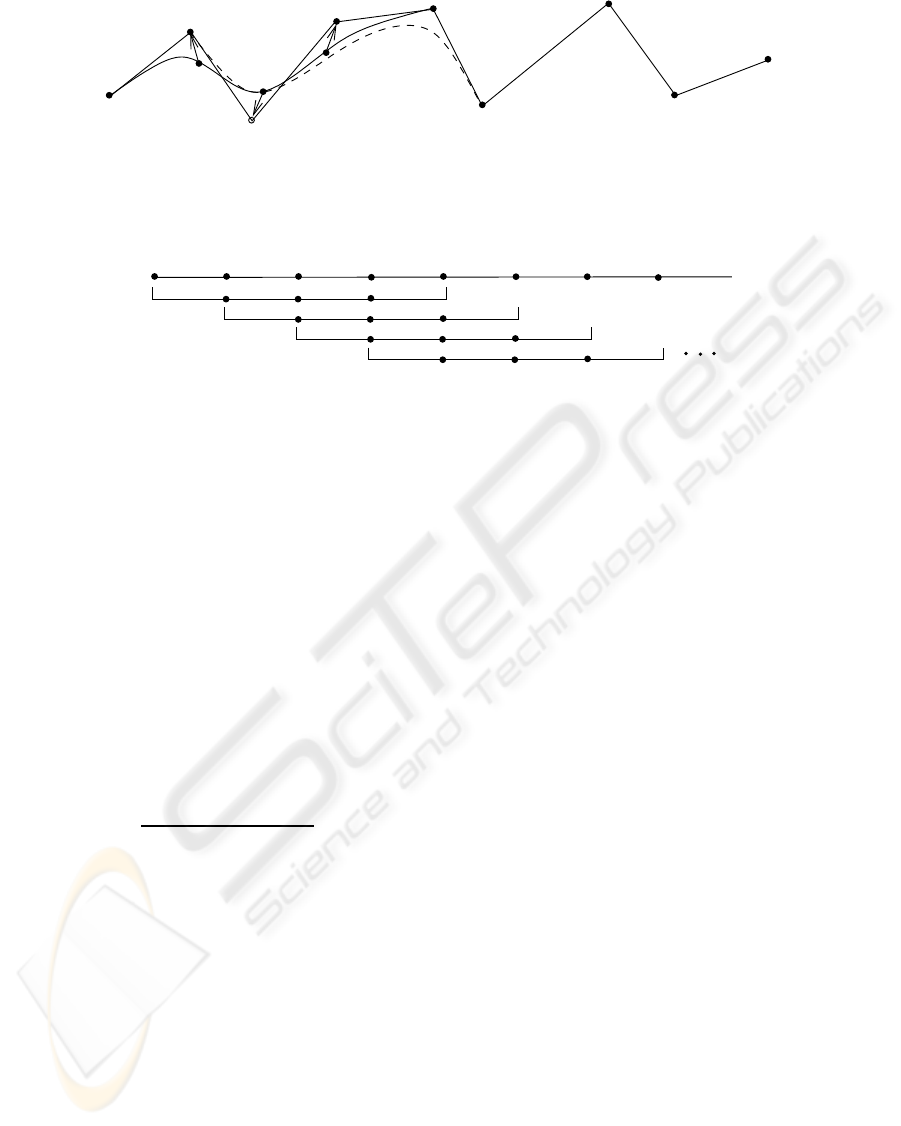
C
0
v
8
5
v
v
v
v
1
2
4
v
6
v
7
c (0.25)
c (0.5)
c (0.75)
0
0
0
3
v
v
Figure 2: The solid curve is c
0
(u), the dashed one c
1
(u), and the arrows point in the direction curvature is lifted (only the
liftings from c
0
(u) are shown).
3
v vv v
0
1
v v
2
3
4
0.2
0.3
0.33
0.5
C
c (u)
c (u)
c (u)
0
1
2
c (u)
Figure 3: Schematic illustration: determining the pseudo-curvature of a polyline vertex from a sliding window of B´ezier
approximations.
lifted. Intuitively, each control vertex picks up its
curvature from the point of the curve at which it has
the most influence. Curvature at the end vertices are
not used on the premise that data from a surround-
ing neighborhood of a point should be available if the
curvature is to be applied for the purpose of simpli-
fication (even though it can be mathematically calcu-
lated).
Figure 2 illustrates the scheme (only the curvature
liftings from the first B´ezier curve are indicated). The
formula used to compute curvature is from classical
differential geometry (Do Carmo, 1976): the curva-
ture of a plane curve c(t) = x(t)i+ y(t)j is given by
κ(t) =
x
′
(t)y
′′
(t) − x
′′
(t)y
′
(t)
(x
′
(t)
2
+ y
′
(t)
2
)
3/2
As the 5-vertex window slides from one end of C
to the other, all the vertices from v
3
to v
n−3
lift cur-
vature values from three different B´ezier curves c
i
(u)
each, while v
0
and v
n
lift no curvature values, v
1
and
v
n−1
lift one each, and v
2
and v
n−2
two each. Figure 3
is a schematic illustration. Heuristically, next, Sim-
pliPoly averages the set of curvature values at each
vertex v
i
(except for v
0
and v
n
, of course) to deter-
mine the so-called pseudo-curvature k
i
, 1 ≤ i ≤ n− 1,
of that vertex, a value used as a curvature estimate.
E.g., if the curvatures values of c
0
(u),c
1
(u),c
2
(u) are
as indicated in Figure 3 (at parameter values 0.75, 0.5
and 0.25, respectively), then the pseudo-curvature of
v
3
is 0.33.
Finally, SimpliPoly removes all vertices v
i
whose
pseudo-curvature k
i
≤ κ, where κ is a user-defined
curvature threshold.
An option in SimpliPoly allows the user to con-
trol in a simple manner the distance error in the sim-
plification as vertices are removed. SimpliPoly re-
moves vertices by processing from the high end to the
low, beginning possibly with v
n−1
. If an error thresh-
old ε > 0 is specified, then, before removing a vertex
v
i
according to the pseudo-curvature constraint, Sim-
pliPoly determines the perpendicular distance d of v
i
to the straight line joining v
i−1
and v
i+1
, and, if this
distance exceeds ε, v
i
is skipped, i.e., not removed.
See Figure 4.
SimpliPoly can be run on-line, or, locally, by
downloading the source – the URL is cited (Sim-
pliPoly, 2006). A Java run-time is required.
3 ANALYSIS
The run-time of SimpliPoly is asymptotically linear
in the number n of vertices of the polyline being sim-
plified. This is trivial to see: there are O(n) window
positions, with a constant amount of curvature com-
putation for the B´ezier curve in each; subsequently,
there is a constant amount of computation per vertex
of the polyline to determine the pseudo-curvature at
that vertex, and process it for possible removal.
Comparison with Douglas-Peucker: For polygonal
curve simplification, Douglas-Peucker (Douglas and
Peucker, 1973) is the algorithm “to beat”. We have
experimented with Douglas-Peucker and SimpliPoly
extensively. From a subjective evaluation of the two
– we compared, therefore, the perceived quality of
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
168

d
v
i
v
i−1
v
i+1
Figure 4: v
i
is not removed if d > ε.
their outputs – SimpliPoly almost always matches
Douglas-Peucker, and is clearly superior in certain
cases for reasons which are not hard to understand,
and which we’ll discuss momentarily.
Theoretically, the worst-case complexity of a
straightforwardrecursive implementationof Douglas-
Peucker is O(mn), where n is the input number of ver-
tices and m the output number. The Douglas-Peucker
worst-case complexity can be improved to O(nlogn)
by using convex hulls to speed up distance compu-
tations (Hershberger and Snoeyink, 1992). As dis-
cussed earlier, SimpliPoly is always O(n), regardless
of output size. However, from our experiments with
up to a few thousand vertices (which bounds the com-
plexity of most practical applications) on a reasonable
desktop, time consumed seems not to be an issue with
either algorithm.
Qualitatively, the major difference between the
two is best seen in a canonical example, as in Fig-
ure 5. The original polyline, which is not drawn, has
the 20 vertices shown. Both SimpliPoly and Douglas-
Peucker were applied to achieve a 60% reduction to
8 vertices, the former by increasing the curvature
threshold, the latter by increasing the distance error
allowed. The SimpliPoly output is the solid line, the
Douglas-Peucker output the dashed one.
As can be seen, SimpliPoly respects the corners
(features) “more” than Douglas-Peucker. The rea-
son, of course, is that the former examines pseudo-
curvatures through a local window, thereby detecting
features that the global Douglas-Peucker method can-
not. On the two straightish (though still mildly noisy)
stretches on either side of the hump both algorithms
perform equally.
4 APPLICATIONS
Curve simplification algorithms are used to reduce
the complexity of 2D graphical scenes in a variety
of application domains. As described in the intro-
duction, curve simplification is often used to pre-
calculate a family of models at successively coarser
levels of detail. This allows an application to dy-
namically make trade-offs between image quality and
performance by choosing between representations of
varying complexity. For example, a drawing program
might use simplified models while the user is interac-
tively scrolling or zooming a scene in order to main-
tain high frame rates.
The main strength of the SimpliPoly algorithm,
when compared with a global error-based algorithm
such as Douglas-Peucker,is its sensitivity to local cur-
vature. This makes it particularly promising for appli-
cations where distinctive local features must be pre-
served. For example, terrain features in cartographic
maps, such as coastlines and elevation lines, are often
”noisy”, with many sharp local changes in direction
that vary in magnitude over the length of the feature.
An error-based algorithm will focus on the vertices
that extend outside a particular tolerance. In contrast,
a curvature-based algorithm will focus on the corners
(the points of high curvature) that define the distinc-
tive shape of the feature. SimpliPoly also includes an
error threshold that can be used interactively to cap-
ture features that change more gradually (regions of
low curvature).
It is difficult for any single algorithm to create a
high-quality simplification for both sharp and grad-
ual changes in curvature. The SimpliPoly software
allows the user to interactively adjust the curvature
and error thresholds of the algorithm to obtain a sim-
plification of the appropriate complexity and qual-
ity. Figure 6 shows a comparison of how the Sim-
pliPoly and Douglas-Peucker algorithms simplify a
curve with both sharp and gradual changes of curva-
ture. In the top example, both algorithms have re-
duced a curve with 58 vertices to 7, a reduction of
87%. The SimpliPoly algorithm is more effective at
capturing the corners of the sharp features, while the
DP algorithm is slightly more effective with the grad-
ual curves. The middle example shows the result of
increasing the number of vertices to 10 (a reduction
of 82%). Both algorithms have improved slightly by
capturing more detail of the sharp and smooth fea-
tures. The bottom example shows the effect of reduc-
ing the error threshold and increasing the curvature
threshold for the SimpliPoly algorithm, which results
SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION
169
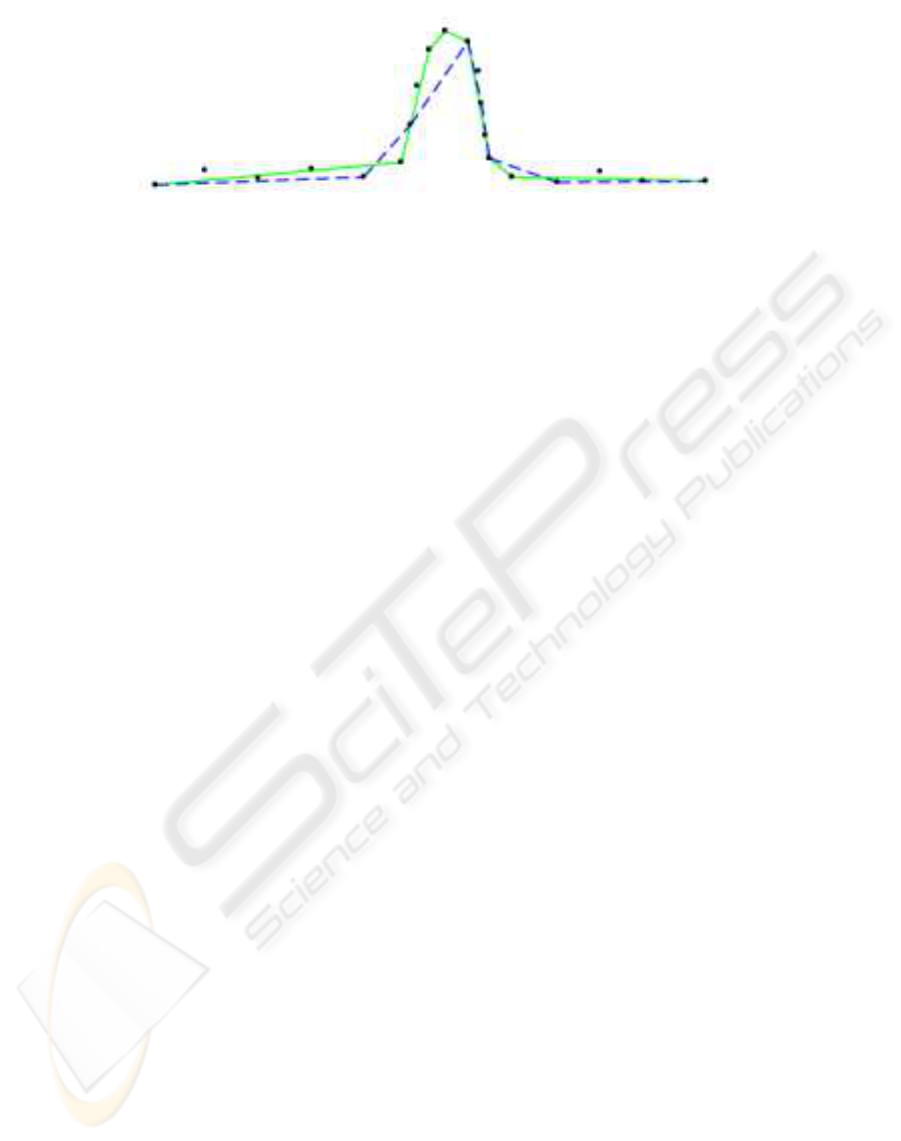
Figure 5: SimpliPoly (solid line) vs. Douglas-Peucker (dashed line): the original polyline (not shown) has 20 vertices (shown),
while both simplifications have 8 vertices each, a reduction of 60%.
in a simplification of equal complexity (10 vertices)
but noticeably better quality.
5 CONCLUSIONS
The primary contribution of this paper is the descrip-
tion of a novel and high-quality curve simplifica-
tion algorithm with a working implementation that is
available for practical use.
The SimpliPoly algorithm is a linear-time 2D
curve simplification method based on curvature es-
timation via piecewise B´ezier approximations. The
software implementation (available on-line at (Sim-
pliPoly, 2006)) allows the user to interactively adjust
the curvature and error thresholds to control trade-offs
between quality and complexity. The algorithm gives
results of comparable – and often superior – quality
to the popular Douglas-Peucker algorithm.
Future work remains to be done, in particular the
following:
1. Empirical evaluation of the algorithm over large
data sets, e.g., Agarwal et al. (Agarwal et al.,
2002) use polygonal curves obtained from the
Protein Data Bank (Protein Data Bank, 2006).
2. Allowing finer control of feature-sensitivity: pos-
sibilities include allowing change in the sliding
window size from its current fixed five, using
curve types other than B´ezier, etc.
3. Hybridizing with a Douglas-Peucker type algo-
rithm, that is more effective in smoothing gradual
(global) changes, to obtain the “ultimate” polygo-
nal curve simplification method.
REFERENCES
Agarwal, P. K., Har-Peled, S., Mustafa, N., and Wang, Y.
(2002). Near-linear time approximation algorithms
for curve simplification. In Tenth European Sympo-
sium on Algorithms, pages 29–41.
Do Carmo, M. P. (1976). Differential Geometry of Curves
and Surfaces. Prentice Hall.
Douglas, D. H. and Peucker, T. K. (1973). Algorithms for
the reduction of the number of points required to rep-
resent a digitized line or its caricature. The Canadian
Cartographer, 10:29–41.
Farin, G. (2001). Curves and Surfaces for CAGD: A Prac-
tical Guide, volume 5. Morgan Kaufmann.
Heckbert, P. S. and Garland, M. (1995). Survey of polyg-
onal surface simplification algorithms. Technical Re-
port CMU-CS-95-194, Carnegie Mellon University.
Hershberger, J. and Snoeyink, J. (1992). Speeding up
the Douglas-Peucker line simplification algorithm. In
Fifth International Symposium on Spatial Data Han-
dling, pages 134–143.
Kim, S.-J., Kim, C.-H., and Levin, D. (2002). Surface sim-
plification using a discrete curvature norm. Computers
& Graphics, 26:657–663.
Luebke, D., Reddy, M., Cohen, J. D., Varshney, A., Watson,
B., and Huebner, R. (2003). Level of Detail for 3D
Graphics. Morgan Kaufmann.
Protein Data Bank (2006). http://www.rcsb.org/pdb/.
SimpliPoly (2006). Polygonal
curve simplification software:
http://www.cs.ait.ac.th/˜ guha/SimpliPoly/simpliPoly.html.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
170

Figure 6: SimpliPoly (solid line) vs. Douglas-Peucker (dashed line) for different curvatures at the same complexity. The
original curve of 58 vertices is reduced to 7 vertices in the top figure and 10 in the bottom two figures. The bottom figure
shows the improvement found with interactively adjusting the error and curvature thresholds of the SimpliPoly algorithm.
SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION
171
