
IMAGE MATTING USING SVM AND NEIGHBORING
INFORMATION
Tadaaki Hosaka†, Takumi Kobayashi†and Nobuyuki Otsu†‡
†National Institute of Advanced Industrial Science and Technology, 1-1-1 Umezono, Tsukuba, Japan
‡University of Tokyo, 7-3-1 Hongo, Tokyo, Japan
Keywords:
Image matting, Markov random field, support vector machine, belief propagation.
Abstract:
Image matting is a technique for extracting a foreground object in a static image by estimating the opacity
at each pixel in the foreground image layer. This problem has recently been studied in the framework of
optimizing a cost function. The common drawback of previous approaches is the decrease in performance
when the foreground and background contain similar colors. To solve this problem, we propose a cost function
considering not only a single pixel but also its neighboring pixels, and utilizing the SVM classifier to enhance
the discrimination between the foreground and background. Optimization of the cost function can be achieved
by belief propagation. Experimental results show favorable matting performance for many images.
1 INTRODUCTION
1.1 Image Matting
Image matting is one of the primary processing tech-
niques in image and video editing. In this problem,
an image is assumed to be a composite of foreground
and background image layers. Let a given image,
the foreground image, and the background image be
denoted by ˜c = (c
1
,c
2
,...,c
N
),
˜
f = ( f
1
, f
2
,..., f
N
),
and
˜
b = (b
1
,b
2
,...,b
N
), respectively. Each element,
c
i
, f
i
, and b
i
(i = 1,2,...,N), is the RGB value (3-
dimensional vector; each pixel value ranges from 0 to
255) of pixel i, and N is the number of pixels. Then,
the observed image ˜c is modeled by the linear com-
bination of a foreground image
˜
f and a background
image
˜
b at each pixel as
c
i
= α
i
f
i
+ (1− α
i
)b
i
, (1)
where α
i
∈ [0, 1] is the mixing rate called alpha value
or opacity. The task of image matting is to estimate
the opacity
˜
α = (α
1
,α
2
,...,α
N
), foreground colors
˜
f, and background colors
˜
b for each pixel in a given
image ˜c.
This task is inherently an under-constrained prob-
lem, since the number of constraints in Eq.(1) is much
less than the number of variables to be estimated
(
˜
α,
˜
f, and
˜
b). Moreover, as the foreground object a
user intends to extract is unknown, the user is usually
required to impose constraints, by indicating parts of
the foreground and background, which provide clues
for classifying the remaining pixels (Figure 1). In this
paper, we utilize this user-input information, as well
as previous approaches.
1.2 Previous Work
Blue screen matting (Smith and Blinn, 1996) was de-
veloped as a technique for motion picture photogra-
phy, which is well known as chroma-key composit-
ing. Recent approaches attempted to extract fore-
ground mattes directly from natural images without
assuming a constant background. Several methods re-
quired a user to prepare a trimap, which is a roughly
segmented map consisting of three regions: definitely
foreground, definitely background, and unknown re-
gions (Figure 1 (b)). Knockout 2 (Berman et al.,
2000) extrapolates the known foreground and back-
ground colors into the unknown region. Ruzon and
Tomasi first introduced a probabilistic view to image
matting, and estimated alpha mattes using foreground
and background distributions around unknown pixels
(Ruzon and Tomasi, 2000). Chuang et al. solved the
matting problem based on the Bayesian framework
344
Hosaka T., Kobayashi T. and Otsu N. (2007).
IMAGE MATTING USING SVM AND NEIGHBORING INFORMATION.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 344-349
Copyright
c
SciTePress

and maximum a posteriori estimation (Chuang et al.,
2001). Sun et al. obtained the alpha matte by solving
the Poisson equation between the gradients of alpha
value and color intensities (Sun et al., 2004). Grady
et al. formulated image matting from the viewpoint of
transition probabilities in random walks (Grady et al.,
2005).
For high-quality matting, users need to carefully
generate the trimap, which is a troublesome and time-
consuming task. This problem was partially solved
by (Wang and Cohen, 2005). In their approach, a
user draws few strokes in the foreground object and
the background, as illustrated in Figure 1 (c), where
pixels on the red strokes are in the foreground, and
those on the blue strokes are in the background. They
defined a cost function for alpha estimation on the
Markov random field (MRF), and minimized it us-
ing the belief propagation (BP) (Pearl, 1988). Re-
cently, under the assumption that the foreground and
background colors lie on a straight line in RGB color
spaces, a closed form solution to image matting has
been derived, and the alpha value was analytically ob-
tained (Levin et al., 2006).
(a) (b) (c)
Figure 1: Methods of indicating the target object. (a) Orig-
inal image. (b) Trimap. A user roughly segments the im-
age into definitely foreground (painted white), definitely
background (painted black), and unknown regions (painted
gray). (c) Input strokes. A user marks the foreground (red
strokes) and background (blue strokes).
1.3 Objective of this Paper
The common drawback of the aforementioned algo-
rithms is that the performance tends to deteriorate
when the foreground and background regions contain
similar colors. One solution is to provide an interac-
tive user interface to modify imperfections, which has
been adopted by Poisson matting (Sun et al., 2004).
In this paper, we aim at improving the perfor-
mance itself using neighboring information around
the referred pixel, while traditional algorithms use
only the information of a single pixel. This exten-
sion, to a certain extent, incorporates texture-like in-
formation into the image matting. Furthermore, we
enhance the discrimination between foreground and
background with support vector machine (SVM).
2 COST FUNCTION
2.1 Formulation
The formulation of our cost function is partially sim-
ilar to (Wang and Cohen, 2005). They considered
two terms in their cost function: the local smooth-
ing term, and the likelihood term which expresses the
sufficiency level of the matting equation (1) when the
alpha value is estimated. However, their formulation
seems so complicated that the essence is slightly am-
biguous.
In this paper, we incorporate three factors into a
cost function for high-quality matting: fidelity to the
matting equation (1), local smoothness, and discrim-
ination based on user inputs. Thus, our cost function
is expressed as
U(
˜
α,
˜
f,
˜
b; ˜c) = λ
M
∑
i∈P
U
M
(α
i
, f
i
,b
i
;c
i
)
+
∑
(ij)∈N
U
S
(α
i
,α
j
;c
i
,c
j
) +λ
D
∑
i∈P
U
D
(α
i
;g
i
), (2)
where U
M
,U
S
, and U
D
express the matting, smooth-
ing, and discrimination terms, respectively. The intro-
duction of the discrimination term is novel to image
matting, and g
i
is the 15-dimensional color vector de-
fined below. The symbols
P and N represent the set
of pixels and adjacent pixel pairs, respectively. The
positive parameters λ
M
and λ
D
control the balance
between these three terms. We specify these terms
below.
2.2 Matting Term
Since the basic assumption of image matting is de-
scribed by Eq.(1), the desirable alpha matte should
satisfy this equation. Here, we explicitly introduce
the fitness of this model using the square error as
U
M
(α
i
, f
i
,b
i
;c
i
) = ||c
i
− α
i
f
i
− (1− α
i
)b
i
||
2
. (3)
2.3 Smoothing Term
The smoothing term is defined as
U
S
(α
i
,α
j
;c
i
,c
j
) =
1
||c
i
− c
j
|| +1
· (α
i
− α
j
)
2
. (4)
This expression means that the smoothness in a given
image ˜c also enforces that in alpha mattes.
2.4 Discrimination Term
2.4.1 Extension of Image Vector
Traditional approaches focused only on the RGB vec-
tor of each pixel. However, including a similar color

in a foreground object and the background makes it
difficult to classify the two regions based on pixel-
wise RGB colors. One solution is to incorporate
neighboring information with pixel-wise colors, and
extract effective features from the local image for nat-
ural image matting.
Based on this perspective, we use the informa-
tion of each pixel and its four nearest neighbors as
one of the straightforward extensions. Although there
are several alternatives for color information, such
as HSV colors and SIFT (Lowe, 2004), we adopt
standard RGB colors to facilitate comparison of our
method with previous work. Therefore, we construct
a 15-dimensional vector consisting of the RGB inten-
sities of each pixel and its four nearest neighbors for
the discrimination term. The array of these vectors
is denoted by ˜g = (g
1
,g
2
,...,g
N
), where g
i
is a 15-
dimensional vector at pixel i.
We expect this configuration to extract some tex-
ture information. It is natural that the RGB color com-
binations among five pixels have more divergences
than in the case of a single pixel, and therefore, ex-
tending 3-dimensional RGB colors to 15-dimensional
vectors provides additional information for more ac-
curate classification.
2.4.2 Classification by Svm
We enhance discrimination between foreground and
background by using the 15-dimensional vectors to
extract effective information for image matting. The
support vector machine (SVM) with the kernel trick
provides a scheme for carrying out this task. In-
put vector ~x is classified by y = Θ[ f
SVM
(~x)], where
y ∈ {0, 1} is a class label, f
SVM
(·) is the SVM output
function, and Θ[z] is 1 for z ≥ 0 or 0 otherwise.
We construct the discrimination term based on the
outputs of the SVM classifier. Note that the train-
ing data consists of the proposed 15-dimensional vec-
tors at user-marked pixels, and class labels express the
foreground (y = 1) and background (y = 0). For pix-
els that a user does not mark, the discrimination term
is defined as
U
D
(α
i
;g
i
) = α
i
d
0
i
+ (1− α
i
)d
1
i
. (5)
In this expression, d
1
i
and d
0
i
represent the affinity of
pixel i to the foreground and the background, respec-
tively. They are defined by the SVM output function
f
SVM
(g
i
) as
d
k
i
i
=
1
1+exp{−a
k
i
| f
SVM
(g
i
)|}
, d
1−k
i
i
= 1−d
k
i
i
, (6)
where k
i
≡ Θ[ f
SVM
(g
i
)] is the classification result.
The coefficients a
1
and a
0
should be determined ap-
propriately; here, we empirically set these parameters
as a
k
i
= 4/J
k
i
, where J
1
and J
0
denote the average val-
ues of the SVM output function for the foreground
and background training data, respectively. In this
study, we adopt the Gaussian kernel (Muller et al.,
2001)
K(~x,~x
′
) = exp
−
||~x−~x
′
||
2
2σ
2
, (7)
where σ is a parameter fixed as σ
2
= 1000 throughout
the paper.
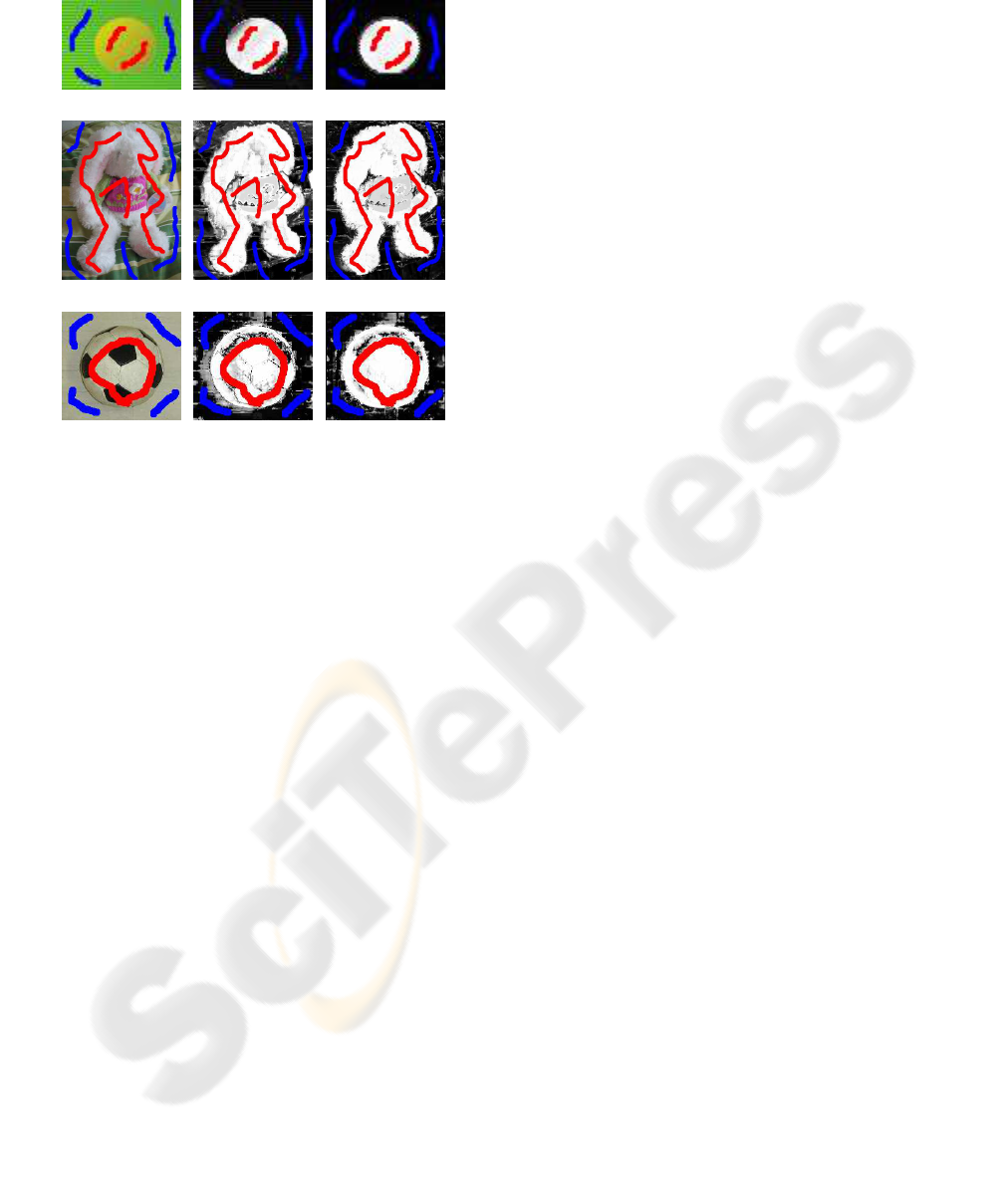
Figure 2 shows the effectiveness of the 15-
dimensional vectors and classification by the SVM.
This figure shows the value of d
1
i
in 256 gray-levels,
when using the standard 3-dimensional RGB vec-
tors ((b), (e), and (h)) and the 15-dimensional ex-
tended vectors (our method, (c), (f), and (i)). Red and
blue strokes indicate user inputs of foreground and
background, respectively. Figure 2(a) is an artificial
graphic produced to help understand the effectiveness
of the proposed 15-dimensional vectors, in which a
foreground object (the yellow ball) exists in a back-
ground texture of a striped pattern of width one pixel.
Since a similar color exists in both the foreground and
background, the performance of pixel-wise methods
degrades (b), while our method (the 15-dimensional
vector and classification by SVM) provides favorable
discrimination result (c) as well as (f) and (i).
3 ALGORITHM
It is difficult to minimize the cost function (2) with
respect to
˜
α,
˜
f, and
˜
b simultaneously. This difficulty
was also faced by (Wang and Cohen, 2005). As they
did, we minimize the cost function for alpha values
using belief propagation (BP) keeping
˜
f and
˜
b fixed,
and minimize the cost function for foreground and
background colors by sampling method keeping
˜
α
fixed.
3.1 Estimation of Alpha Values By Bp
Finding optimal alpha mattes with minimum cost cor-
responds to the MAP estimation problem, which is
generally computationally difficult. Thus, we have to
employ practically tractable algorithms that generate
(sub)optimal solutions.
For discrete combinatorial optimization, the belief
propagation (Pearl, 1988) is a promising approach for
such tasks. BP has been recently exploited for vari-
ous computer vision problems (e.g., stereo matching
(Sun et al., 2003)) as well as image matting (Wang
and Cohen, 2005). Therefore, we quantize the alpha
value to 11 levels (at 0.1 intervals between 0 and 1), in
original images
with user inputs
3-dimension 15-dimension
(a) (b) (c)
(d) (e) (f)
(g)
(h) (i)
Figure 2: Comparison among the discrimination terms. The
pixel in white indicates an affinity for the foreground and
the pixel in black indicates that for the background. Tra-
ditional 3-dimensional RGB (b) are insufficient to sepa-
rate the foreground object from the background texture in
the toy example shown in (a), whereas the proposed 15-
dimensional vectors (c) provide excellent classification. In
the example of the stuffed rabbit, although the difference is
not necessarily clear, we can see some places in the back-
ground where the 15-dimensional case (f) is superior to the
3-dimensional case (e). In the soccer ball image, the 3-
dimensional vectors misclassify pixels to the left of the ball
(h).
order to transform the current problem into a discrete
combinatorial optimization.
On the current MRF, BP is represented as a mes-
sage passing algorithm between neighboring pixels:
m
t
ij
(α
i
) = min
α
j
λ
M
U
M
(α
j
, f
j
,b
j
;c
j
)/Z
j
+λ
D
U
D
(α
j
;g
j
) +U
S
(α
i
,α
j
;c
i
,c
j
)
+
∑
k∈N ( j)\i
m
t−1
jk
(α
j
), (8)
where N ( j)\i denotes the set of nearest neighbors of
pixel j other than i, and t = 1,2,... is an index for
iteration steps. The matting term U
M
is normalized
by a factor Z
j
≡
∑
α
′
||c
j
− α
′
f
j
− (1− α
′
)b
j
||
2
to re-
strict this term to a range [0,1] as well as the other
two terms (U
D
and U
S
) and facilitate the adjustment
of parameters λ
M
and λ
D
.
Note that the messages m
t
ij
and m
t
ji
are different
variables. After the convergence of the iterations, a
belief vector is computed for each pixel as
b
i
(α
i
) = λ
M
U
M
(α
i
, f
i
,b
i
;c
i
)/Z
i
+ λ
D
U
D
(α
i
,g
i
)
+
∑
j∈N (i)
m
∗
ij
(α
i
), (9)
where the superscript * represents the value at conver-
gence, and the optimal label at pixel i, denoted as α
∗
i
,
is estimated as
α
∗
i
= argmin
α
i
b
i
(α
i
). (10)
As used in (Wang and Cohen, 2005), we employ the
techniques proposed by (Felzenszwalb and Hutten-
locher, 2004) to facilitate the calculation of Eq.(8)
3.2 Sampling for Foreground and
Background Colors
We must estimate the foreground and background col-
ors,
˜
f and
˜
b as well as alpha values. Foreground and
background colors appear only in the matting term.
We determine these values by a sampling approach.
Let the current value of the matting term at pixel i
be denoted as v
i
≡ ||c
i
−α
i
f
i
−(1−α
i
)b
i
||
2
. For each
pixel i, we sequentially search the optimal foreground
and background colors in its neighboring pixel j from
the nearest neighbors within a radius of 20 pixels. We
focus f
j
if α
j
> α
i
(or b
j
if α
j
< α
i
), and replace the
foreground (background) colors f
i
(b
i
) with f
j
(b
j
) if
the matting term is reduced, i. e.,
||c
i
− α
i
f
j
− (1− α
i
)b
i
||
2
< v
i
(||c
i
− α
i
f
i
− (1− α
i
)b
j
||
2
< v
i
).
3.3 Algorithm Flow
We use the multiscale technique proposed by (Felzen-
szwalb and Huttenlocher, 2004) to facilitate the com-
putation and obtain better results. We begin with an
estimation for the coarsest image, and use the results
as initial values for the finer image. The final alpha
matte is obtained as a result of the original scale. Our
entire algorithm is described below.
1) Generation of multiscale images Multiscale im-
ages for an original image and the user strokes are
generated by the standard quad-tree method.
2) Classification by SVM The elements of the dis-
crimination term d
1
i
and d
0
i
are calculated.
3) Initialization We set f
i
= c
i
for user-marked fore-
ground pixels, and b
i
= c
i
for user-marked back-
ground pixels. Unmarked pixels take over the val-
ues of corresponding pixels at the previous coarser
scale.

original images
with user inputs
Wang and Cohen Levin et al. our method
Figure 3: Examples of experimental results. The first column shows original images with user-specified strokes. The other
columns show the results of (Wang and Cohen, 2005), (Levin et al., 2006), and our method. The parameters λ
M
and λ
D
as
well as those included in the two previous approaches are adjusted so that the performance is optimal by appearance.
4) Estimation of alpha values The alpha values are
estimated by the BP with foreground and back-
ground colors fixed.
5) Estimation of foreground and background colors
The foreground and background colors are esti-
mated by sampling from neighboring pixels with
the alpha values fixed.
6) Repeat the steps 4 and 5 until the values of
˜
α,
˜
f,
and
˜
b remain constant.
7) Return to the step 3 and start the estimation for the
next finer scale.
4 EXPERIMENTAL RESULTS
The proposed approach has been tested for various
images. Figure 3 shows several results obtained by
our method, compared to other methods, (Wang and
Cohen, 2005) and (Levin et al., 2006). The results
of these previous works were obtained using the pro-
grams provided on their websites. There are four
multiscales for every image. The upper three exam-
ples were also used in the previous works, and we
set user-marked inputs in places similar to those stud-
ies. The parameters λ
M
and λ
D
in Eq.(2) were de-
termined manually for each image so that the perfor-
mance is optimal by appearance, and the parameters
in the other methods were also optimized by hand.
It is basically difficult to obtain ground truth and
quantitatively evaluate matting performance. There-
fore, we resort to subjective evaluation. Previous ap-
proaches work well on the images of a peacock and
a face, and our approach also compares favorably on
those images. In the latter two images which con-
tain similar colors in the foreground and background,
our method extracts the foreground object better than
the other algorithms on the whole, which indicates
that the proposed 15-dimensional color vectors and
classification by SVM are effective for image mat-
ting. However, in some instances, our method does
not necessarily capture the details as well as the other
methods. Figure 4 shows an example of a compos-
ite image, the stuffed rabbit extracted by our method

with a blue background. The enlarged details in the
red square are relatively reasonable, while those in the
green square are missing in the composite image.
The performance of these matting algorithms de-
pends on the positions and the quantity of the user
inputs. In particular, when a user draws only a few
strokes, the performance can deteriorate drastically.
An example of the calculation time is as follows.
Using a 2.66 GHz CPU with 3 GB RAM, an image
size of 341×455 pixels (the stuffed rabbit in Figure 3)
requires about 23 sec for the classification by SVM
and about 17 sec for the subsequent estimation by
BP and sampling without specific programming op-
timization.
5 CONCLUSION
This paper has proposed the improvement of the cost
function for image matting. A key contribution is the
use of neighboring information in terms of higher di-
mensional vectors, instead of considering the infor-
mation in a single pixel. In addition, we enhanced the
discrimination between foreground and background
with SVM. We obtained high-quality matting results
even when a foreground object and background had
similar colors.
Our future work includes further improvements
to the cost function and estimation process for fore-
ground and background colors, in order to obtain
more desirable results. Setting the parameter values
also influences matting results. In this study, we man-
ually set optimal values for λ
M
and λ
D
, which may
not be implemented in practice. Statistical inference
methods, such as the maximum of marginal likelihood
(Tanaka, 2002) could be used for this parameter esti-
mation. Another problem is the optimal setting of the
parameters σ and a
k
i
in the SVM formulation. Cross
validation method is one promising solution for this
problem.
composite image
enlarged
(composite)
enlarged
(original)
Figure 4: An example of composite images with blue back-
ground. It can be seen that some details in the original im-
age are missing in the composite image.
ACKNOWLEDGEMENTS
The study was supported by the advanced surveil-
lance technology project of MEXT. The authors thank
T. Kurita and N. Ichimura for their helpful discus-
sions.
REFERENCES
Berman, A., Vlahos, P., and Dadourian, A. (2000). Com-
prehensive method for removing from an image the
background surrounding a selected object. In U. S.
Patent, 6, 134, 345.
Chuang, Y. Y., Curless, B., Salesin, D., and Szeliski, R.
(2001). A bayesian approach to digital matting. In
Proc. of IEEE CVPR. pp. 264-271.
Felzenszwalb, P. F. and Huttenlocher, D. P. (2004). Efficient
belief propagation for early vision. In Proc. of IEEE
CVPR. pp. 261-268.
Grady, L., Schiwietz, T., Aharon, S., and Westermann, R.
(2005). Random walks for interactive alpha-matting.
In Proc. of VIIP05. pp. 423-429.
Levin, A., Linschinski, D., and Weiss, Y. (2006). A closed
form solution to natural image matting. In Proc. of
IEEE CVPR. pp. 61-68.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. In International Journal of Com-
puter Vision. vol. 60, pp. 91-110.
Muller, K. R., Mika, S., Ratsch, G., Tsuda, K., and
Scholkopf, B. (2001). An introduction to kernel-based
learning algorithms. In IEEE Trans. on Neural Net-
works. vol. 12, pp. 181-201.
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Sys-
tems. Morgan-Kauffman, San Francisco.
Ruzon, M. A. and Tomasi, C. (2000). Alpha estimation in
natural images. In Proc. of IEEE CVPR. pp. 18-25.
Smith, A. R. and Blinn, J. F. (1996). Blue screen matting. In
Proc. of the 23rd annual conf. on Computer graphics
and interactive techniques. pp. 259-268.
Sun, J., Jia, J., Tang, C. K., and Shum, H. Y. (2004). Poisson
matting. In Proc. of ACM SIGGRAPH. pp. 315-321.
Sun, J., Zheng, N. N., and Shum, H. Y. (2003). Stereo
matching using belief propagation. In IEEE Trans.
on PAMI. vol. 25, pp. 787-800.
Tanaka, K. (2002). Theoretical study of hyperparameter
estimation by maximization of marginal likelihood
in image restoration by means of cluster variation
method. In Electronics and Communications in Japan.
vol. 85, pp. 50-62.
Wang, J. and Cohen, M. F. (2005). An iterative optimization
approach for unified image segmentation and matting.
In Proc. of IEEE ICCV. pp. 936-943.
