LEFT VENTRICLE IMAGE LANDMARKS EXTRACTION USING
SUPPORT VECTOR MACHINES
Miguel A. Vera
Laboratorio de F´ısica
Departamento de Ciencias, Universidad de Los Andes–T´achira, San Crist´obal 5001, Venezuela
Antonio J. Bravo
Grupo de Bioingenier´ıa
Decanato de Investigaci´on, Universidad Nacional Experimental del T´achira, San Crist´obal 5001, Venezuela
Keywords: Human heart, anatomical landmarks, left ventricle, patterns classification, support vectors machines.
Abstract:
This paper introduces an approach for efficient myocardial landmarks detection in angiograms. Several
anatomical landmarks located on the left ventricle are obtained by mean of a support vector machine. Training
set corresponds a dataset of landmark and non-landmark 31×31 pixel patterns. Our support vector machine
uses the structural risk minimization principle as inference rule and radial basis function kernel. In the training
phase false positives were not registered and in the detection phase 100% of recognition was obtained.
1 INTRODUCTION
Landmarks detection from medical images represents
a stage useful stage to extracting sufficient informa-
tion which describes an examined anatomical struc-
ture. The extracted image landmarks are used in va-
rious applications of medical image analysis, such
as segmentation (Bosch et al., 2002), shape–model
construction (Frangi et al., 2002) and motion analy-
sis (Chandrashekara et al., 2004).
In clinical routine cardiologist uses heart cavities
images for the assessment of morphology and func-
tion of the heart (Marcus and Dellsperger, 1991).
Contrast cineangiography based on X–rays provide
a projected image of the cardiac structures (Macov-
ski, 1983). These images have enough information of
dimension and shape of heart cavities during the en-
tire cardiac cycle. The left ventricle is considered the
main cavity of the heart.
Left ventricle images are obtained from cinean-
giography, after the injection of a contrast medium in
the cavities of the heart aiming to enhance the contrast
with respect to other tissues. Ventriculographic ima-
ge analysis requires a precise description of ventricu-
lar shape in order to quantify the parameters associa-
ted with the cardiovascular function (Kennedy et al.,
1970) (Ratib, 2000) or alternatively for performing
the visualization of this anatomical structure (Medina
et al., 2004). The accurate description of ventricu-
lar shape and their quantitative analysis is important,
since cardiovascular disease (CVD) accounts for one
third of the deaths in the world (WHO, 2002).
Recently, several robust methods for ventricu-
lographic image segmentation have been proposed.
Suzuki et al. (Suzuki et al., 2004) have developed
a ventricular contour detector based on neural net-
works (NN). The detector was implemented using a
multilayer neural network which was trained through
a back–propagation algorithm. The training set in-
cludes left ventricle images and ventricular contours
traced by a cardiologist. Validation was performed by
comparison of the area enclosed by the estimated con-
tour with respect to the reference contour traced by
the cardiologist. The average contour error obtained
at end–diastole was 6.2%. Oost et al. (Oost et al.,
2005) have proposed a ventricular cavity automatic
segmentation method based on Active Appearance
Models (AAMs) and dynamic programming (DP).
The active appearance model is used to exploit the ex-
isting correlations in shape and texture between end-
diastole and end-systole images. A dynamic program-
ming algorithm was used to incorporate cardiac mo-
tion features to the method. The method was evalua-
ted by using 140 images. The average border posi-
tioning error was smaller than 1.45 mm. These me-
thods provided an accurate representation of ventri-
cular borders, however,they are not yet fully validated
and accepted by clinicians as a gold standard.
339
A. Vera M. and J. Bravo A. (2007).
LEFT VENTRICLE IMAGE LANDMARKS EXTRACTION USING SUPPORT VECTOR MACHINES.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 339-343
Copyright
c
 SciTePress

Segmentation techniques some times require a
previous stage in which an initial set of points is lo-
cated near the shape to detect (Fu and Mui, 1981). In
cardiac imaging left ventricle anatomical landmarks
as apex, basal regions and aortic valve points are use-
ful to define the left ventricle shape.
The objective of this work is to develop an ap-
proach based on machines learning to detecting seve-
ral anatomical landmarks located on the left ventri-
cle (LV) contour. This is a classification problem be-
cause the machine learning task is to classify example
among a discrete set of possible categories or classes.
Our approach utilizes densitometric information and
a support vector machine (SVM) for the reliable lo-
calization of landmarks in ventriculographic images.
2 SUPPORT VECTOR MACHINES
Support Vector Machine (SVM) is a learning tech-
nique based in the framework of statistical learning
theory (Vapnik, 1995). These machines learning can
be seen as a method for training polynomial, neural
network or radial basis function classifiers. The SVM
training process is based on the idea of minimizing
an upper bound on the generalization error by mean
structural risk minimization induction principle (Vap-
nik, 1982).
SVMs have been applied successfully in practical
problems such as pattern classification (Osuna et al.,
1997b) and nonlinear function estimation problems
(Smola, 1998). A classifier based on SVM is a ma-
chine learning that uses a hyperplane to separate pa-
tterns classes (Burges, 1998). If the classification task
is a two–class pattern recognition problem, where we
assume that we have a set of examples:
z
i
=

{x
i
,y
i
} | x
i
∈ R
N
∧ y
i
∈ {−1,+1} ∧ i = 1..l

the hyperplane corresponds to a decision function:
f
α
(x) : R
N
−→ {−1,+1} . (1)
which provides the smallest possible value for the risk
(Sch¨olkopf et al., 1995). The SVM classifier is de-
fined by the family function f
α
(x) which mappings
x
i
7→ y
i
. A deterministic process is implanted to reach
the machine’s task: to learn the mapping x
i
7→ y
i
. In
this process given a set of examples x, a particular
value of the α parameter is chosen for the same out-
put f
α
(x). The process to choice a α that mapping
x
i
7→ f
α
(x) is an optimization process called Training
a Support Vector Machine (Osuna et al., 1997b).
For linearly separable data, the classification pro-
blem is solved finding the best hyperplane that sep-
arates the data. Osuna and collaborators (Osuna
et al., 1997a) show that the decision surface in the
linear case using Lagrange Multipliers like optimiza-
tion technique can be written as:
f
α
(x) = sign
l
∑
i=1
y
i
λ
i
(x· x
i
) + b
!
, (2)
where λ
i
are non–negative Lagrange multipliers.
The main problem in real classification task is that
linear decision surfaces (hyperplane) are not appro-
priate. In this case is necessary to map the dataset to
higher dimensional feature space (some other Euclid-
ean space ℜ) using the following mapping:
Φ : R
N
7→ ℜ . (3)
In the feature space we work with linear classifi-
cation. For that reason, the so–called kernel function
(K) is introduced to compute scalar products of the
form Φ(x
i
) · Φ(x
j
):
K(x
i
,x
j
) ≡ Φ(x
i
) · Φ(x
j
) . (4)
Using (2) and (4) the SVM solution is expressed
as:
f
α
(x) = sign
l
∑
i=1
y
i
λ
i
(K(x,x
i
)) + b
!
. (5)
In pattern recognition problem several kernels
have been applied (Burges, 1998). The kernels for
which (3) is verified are all those that satisfy the Mer-
cers’s condition (Vapnik, 1995; Williamson et al.,
1999). Some commonly used kernels:
K(x
i
,x
j
) = (x
i
· x
j
+ 1)
p
. (6)
K(x
i
,x
j
) = tanh(x
i
· x
j
− θ) . (7)
K(x
i
,x
j
) = e
−kx
i
−x
j
k
2
/2σ
2
. (8)
A SVM polynomial classifier of degree p is cons-
tructed using (6). (7) results in a particular multi layer
perceptron only for some values of θ, and (8) gives
a radial basis function classifier. Other valid kernel
functions that satisfy Mercer’s conditions are (Gunn,
1997):
• Exponential radial basis function:
K(x
i
,x
j
) = e
−kx
i
−x
j
k/2σ
2
• Fourier series:
K(x
i
,x
j
) =
sin

N +
1
2

(x
i
− x
j
)
sin(
1
2
(x
i
− x
j
)

• B–splines:
K(x
i
,x
j
) = B
2N+1
(x
i
− x
j
)
• Additive kernels:
K(x
i
,x
j
) =
∑
l
K
l
(x
i
,x
j
)
• Tensor product:
K(x
i
,x
j
) =
∏
l
K
l
(x
i
,x
j
)
3 PROPOSED APPROACH
The learning task here involves classifying patterns
that represent left ventricle landmarks on ventriculo-
graphycs images.
3.1 Data Source
The images used are sequences of ventriculographics
images acquire on patients using a digital flat–panel
X–ray system (Innova
TM
4100 General Electric Me-
dical System). These images were acquired from
Right Anterior Oblique (RAO 30
◦
) direction. Each
image with resolution of 420×420 pixels and with
each image pixel described by a greyscale intensity
value between 0 (black) and 255 (white). Figure 1
shows angiographics images of the left ventricle in
RAO incident.
Figure 1: Left ventricle images. Systole phase (left). Dias-
tole phase (right).
3.2 Training Set Selection
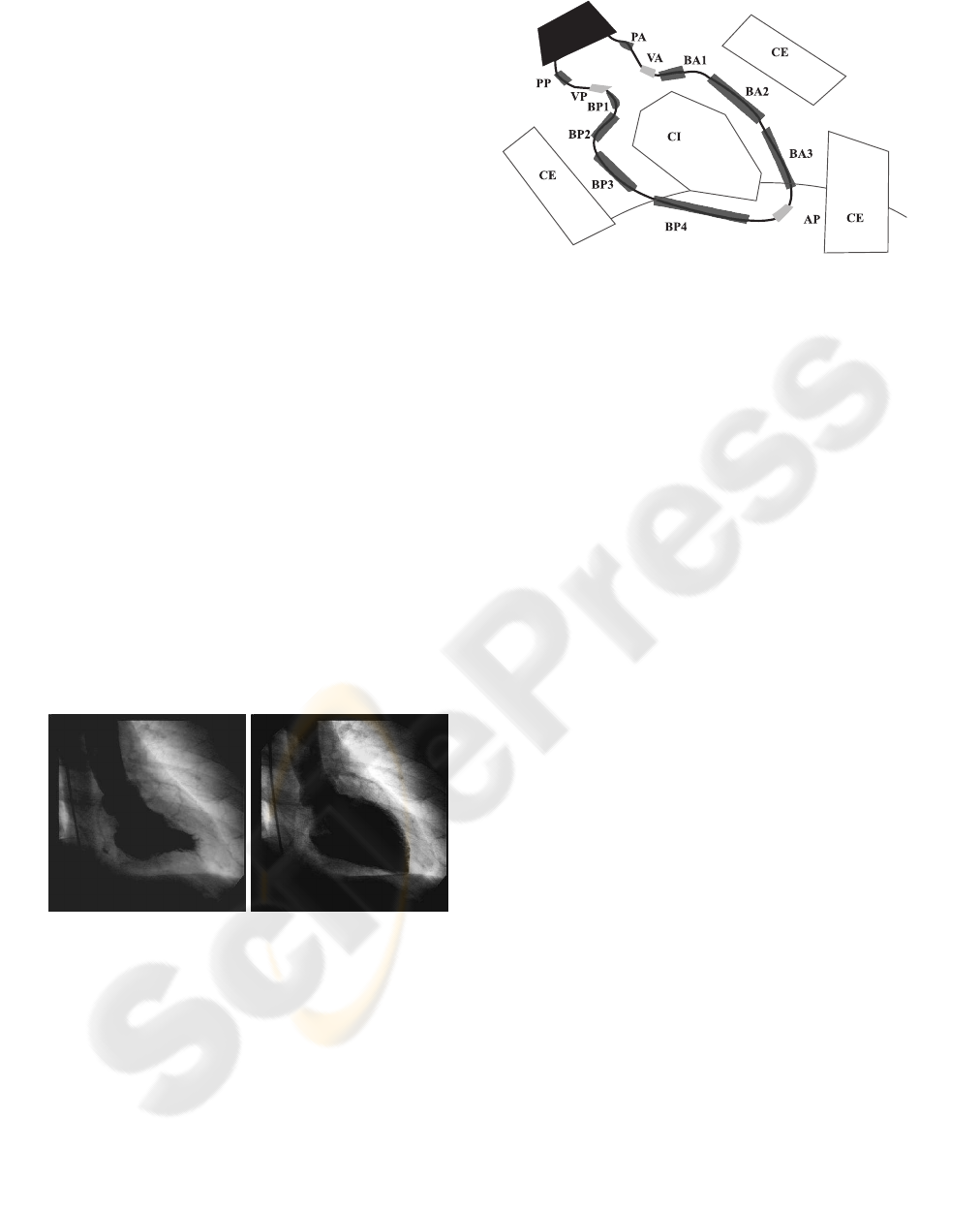
American Heart Association (AHA) establishes fif-
teen anatomical landmarks for the left ventricle shape
definition on the angiographic images acquired from
RAO 30
◦
direction.
The selected landmarks correspond to apex (AP),
the basal regions (BA2, BP3, BP4) and the aortica
valve sides (VA, VP). Dataset of landmarks patterns
Figure 2: AHA anatomical landmarks.
is constructed from a ventriculographic image se-
quence. A manually process driven by a cardiolo-
gist is applied to locate 31×31 pixel patterns corres-
ponding to each LV landmark. A total of 300 pa-
tterns constitutes the landmarks dataset, 50 images of
31×31 pixel for each landmark. Applying a similar
procedure, a dataset of 1200 non–landmark images
was generated from angiographic images of coronary
vessel and kidney. A training set is formed in rela-
tion 1:4, by each pattern that represents an anatomical
landmark, four non–landmark images are introduced.
Class +1 is assigned to identify a landmark and class
-1 for the non–landmark.
3.3 Training a Support Vector Machine
In this Section we design a SVM using the library
for Support Vector Machines of MatLab 7.0. The
idea is to construct a SVM classifier using one of the
most popular parametric kernel: Gaussian radial basis
function (8).
This implementation considers a unique parame-
ter σ. Additionality, our SVM classifier considers a
misclassification tolerance parameter C that penali-
zing the most undesirables errors. A large value of
this parameter corresponding a higher penalty errors.
The SVM is trained using a training set of 1500
patterns (see section 3.2). The training process is used
to construct a decision surface that allows to classify
the input images as left ventricle landmark or non–
landmark.
The bootstrapping step is applied. The decision
surface obtained in the training process is used to
classify images that do not contain landmarks. The
false positive obtained in this process are incorporated
to dataset of non–landmark images and used in sub-
sequent training phases. This bootstrapping process
helps to characterize and define the non–landmark
class in order to obtain the decision surface than better

separates the classes. Non–landmark class is abun-
dant and broader in this sense more complex that
landmark class.
3.4 The Svm Left Ventricle Landmark
Detection Approach
Our landmark extraction problem can be defined as
follows: Given a ventriculographic image which is
consider as input data, determine where the LV’s
landmarks in this image are located and return an en-
coding of their location. Our encoding is to represent
each anatomical landmark on the image by means of
31×31 pixel bounding box whose center represents
the exact location of the landmark.
This approach detects left ventricle landmarks by
exhaustively scanning an image for landmark–like
patterns, by splitting the original image into overla-
pping sub–images and classifying them using a SVM
(see section 3.3) to determine the appropriate class
(landmark or non–landmark).
4 RESULTS
The training of support vector machine was per-
formed using the MATLAB Support Vector Machine
toolbox developed by Gunn (Gunn, 1997) from the
Information: Signals, Images, Systems (ISIS) Re-
search Group at the University of Southampton. A
SVM classifier was trained considering σ = 0.002 and
C = 10.
The landmark detection stage was implemented in
MatLab. The support vector obtained in the training
stage are used to construct the decision surface that
we use to discriminate if each subimage (see section
3.4) of the original image is a left ventricle landmark
or non–landmark.
The proposed approach has been tested with ven-
triculograms acquired at several instants of the car-
diac cycle. During the training procedure false posi-
tives were not registered. In the landmark extraction
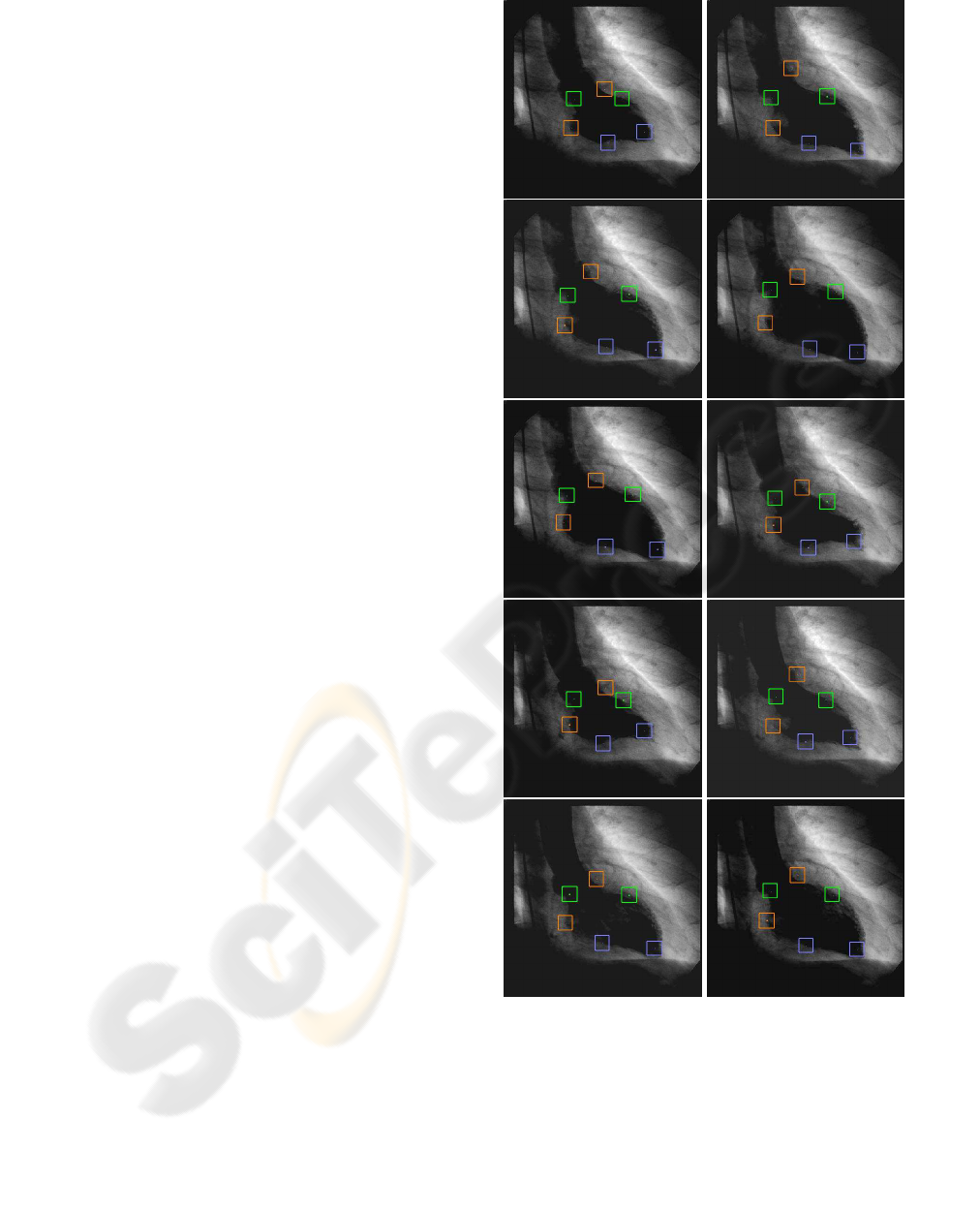
phase 100 % of recognition was obtained. In figure
3, results of the left ventricle images landmarks ex-
traction approach for the end–systole to end–diastole
ventriculogram sequence are shown.
Validation of the approach is performed by quan-
tifying the difference between the left ventricle land-
mark location obtained with respect to the left ventri-
cle landmark located by a cardiologist. The error is
expressed as the distance between the manual and au-
tomatic landmark location. The error obtained (mean
± standard deviation) for a sequence of ventriculo-
grams in the RAO view, including 21 images is 2.47
Figure 3: Left ventricle image sequence. Bounding boxes
represents the anatomical landmarks obtained.
mm ± 1.61 mm, with a maximum value of 4.84 mm
and a minimum value of 1.03 mm.

5 CONCLUSIONS
An automatic approach for left ventricle anatomical
landmarks extraction has been implemented. The
classification approach does not require any prior
knowledge about the ventriculograms and not require
some preprocessing of the input data.
A quantitative validation stage is implemented.
The estimated landmarks from the detection approach
show a good match with the landmarks located by
specialist. This application would be a useful tool for
detecting the left ventricle landmark in conventional
Left Anterior Oblique (LAO) 60
◦
view.
Further research involves incorporationof the pro-
posed classifier to an approach for left ventricle con-
tour detection using deformable models.
ACKNOWLEDGEMENTS
The authors would like to thank the CDCHT from
Universidad de Los Andes–T´achira and Investigation
Dean’s Office of Universidad Nacional Experimental
del T´achira. Authors would also like to thank the Cen-
tro M´edico Caracas in Caracas, Venezuela for provi-
ding the human ventriculographic databases.
REFERENCES
Bosch, J., Mitchell, S., Lelieveldt, B., Nijland, F., Kamp,
O., Sonka, M., and Reiber, J. (2002). Automatic seg-
mentation of echocardiographic sequences by active
appearance motion models. IEEE Transactions on
Medical Imaging, 21(11):1374–1383.
Burges, C. (1998). A tutorial on support vector machines for
pattern recognition. Knowledge Discovery and Data
Mining, 2(2):121–167.
Chandrashekara, R., Mohiaddin, R., and Rueckert, D.
(2004). Analysis of 3–D myocardial motion in tagged
MR images using nonrigid image registration. IEEE
Transactions on Medical Imaging, 23(10):1245–1250.
Frangi, A., Rueckert, D., Schnabel, J., and Niessen, W.
(2002). Automatic construction of multiple-object
three-dimensional statistical shape models: Applica-
tion to cardiac modeling. IEEE Transactions on Med-
ical Imaging, 21(9):1151–1166.
Fu, K. S. and Mui, J. K. (1981). A survey on image seg-
mentation. Pattern Recognition, 13(1):3–16.
Gunn, S. (1997). Support vector machines for classification
and regression. Technical report, Information: Sig-
nals, Images, Systems (ISIS) Research Group, Uni-
versity of Southampton.
Kennedy, J., Trenholme, S., Kaiser, I., and Wash, S. (1970).
Left ventricular volume and mass from single–plane
cineangiocardiogram. A comparison of anteroposte-
rior and right anterior oblique methods. American
Heart Journal, 80(3):343–352.
Macovski, A. (1983). Medical Imaging Systems. Prentice-
Hall, New-Jersey.
Marcus, M. L. and Dellsperger, K. C. (1991). Determinants
of systolic and diastolic ventricular function. In Mar-
cus, M., Schelbert, H., Skorton, D., and Wolf, G., ed-
itors, Cardiac Imaging. A Companion to Braunwald’s
Heart Disease, pages 24–38. W.B. Saunders Com-
pany, Philadelphia, USA.
Medina, R., Garreau, M., Toro, J., Coatrieux, J. L., and
Jugo, D. (2004). Three–dimensional reconstruction
of left ventricle from two angiographic views: An ev-
idence combination approach. IEEE Transactions on
Systems, Man, and Cybernetics—Part A: Systems and
Humans, 34(3):359–370.
Oost, E., Koning, G., Sonka, M., Reiber, J., and Lelieveldt,
B. (2005). Automated segmentation of X–ray left ven-
tricular angiograms using multi–view active appear-
ance models and dynamic programming. In Proceed-
ings of the Functional Imaging and Modeling of the
Heart: Third International Workshop, pages 23–31,
Barcelona, Spain.
Osuna, E., Freund, R., and Girosi, F. (1997a). Support vec-
tor machines: Training and applications. Technical re-
port, Artificial Intelligence Laboratory, Massachusetts
Institute of Technology.
Osuna, E., Freund, R., and Girosi, F. (1997b). Training sup-
port vector machines: an application to face detection.
In Conference on Computer Vision and Pattern Recog-
nition (CVPR ’97), pages 130–136, San Juan, Puerto
Rico.
Ratib, O. (2000). Quantitative analysis of cardiac function.
In Bankman, I., editor, Handbook of Medical Imag-
ing: Processing and Analysis, pages 359–374. Acad-
emic Press, San Diego.
Sch¨olkopf, B., Burges, C., and Vapnik, V. (1995). Extract-
ing support data for a given task. In Proceedings First
International Conference on Knowledge Discovery &
Data Mining, pages 252–257, Menlo Park, CA.
Smola, A. J. (1998). Learning with Kernels. PhD thesis,
Technische Universitt Berlin, Germany.
Suzuki, K., Horiba, I., Sugie, N., and Nanki, M. (2004). Ex-
traction of left ventricular contours from left ventricu-
lograms by means of a neural edge detector. IEEE
Transactions on Medical Imaging, 23(3):330–339.
Vapnik, V. (1982). Estimation of Dependences Based on
Empirical Data. Springer–Verlag, New York.
Vapnik, V. (1995). The Nature of Statistical Learning The-
ory. Springer–Verlag, New York.
WHO (2002). Reducing risk and promoting healthy
life. The World Health Report 2002, Geneva, World
Health Organization.
Williamson, R., Smola, A., and Sch¨olkopf, B. (1999). En-
tropy numbers, operators, and support vector kernels.
In Sch¨olkopf, B., Burges, C., and Smola, A., editors,
Advances in Kernel Methods–Support Vector Learn-
ing, pages 127–144, Cambridge, MA: MIT Press.