BIASED MANIFOLD EMBEDDING FOR PERSON-INDEPENDENT

HEAD POSE ESTIMATION

Vineeth Nallure Balasubramanian and Sethuraman Panchanathan

Center for Cognitive Ubiquitous Computing (CUbiC), School of Computing and Informatics

Arizona State University, Tempe, AZ 85281, USA

Keywords:

Manifold learning, Non-linear dimensionality reduction, Face modeling and analysis, Head pose estimation,

Regression analysis.

Abstract:

Head pose estimation is an integral component of face recognition systems and human computer interfaces.

To determine the head pose, face images with varying pose angles can be considered to lie on a smooth

low-dimensional manifold in high-dimensional feature space. In this paper, we propose a novel supervised

approach to manifold-based non-linear dimensionality reduction for head pose estimation. The Biased Man-

ifold Embedding method is pivoted on the ideology of using the pose angle information of the face images

to compute a biased geodesic distance matrix, before determining the low-dimensional embedding. A Gener-

alized Regression Neural Network (GRNN) is used to learn the non-linear mapping, and linear multi-variate

regression is ﬁnally applied on the low-dimensional space to obtain the pose angle. We tested this approach

on face images of 24 individuals with pose angles varying from -90

◦

to +90

◦

with a granularity of 2

◦

. The re-

sults showed signiﬁcant reduction in the error of pose angle estimation, and robustness to variations in feature

spaces, dimensionality of embedding and other parameters.

1 INTRODUCTION

As human-centered computing applications grow

each day, human face analysis has grown in its impor-

tance as a problem studied by several research com-

munities. The estimation of head pose angle from

face images is a signiﬁcant sub-problem in this re-

spect in several applications like 3D face modeling,

gaze direction detection, driver monitoring safety sys-

tems, etc. Further, realistic solutions to the problem

of face recognition have to be able to handle signiﬁ-

cant head pose variations, thereby leading to the gain

in importance of the automatic estimation of the ori-

entation of the head relative to the camera-centered

co-ordinate system. While coarse head pose estima-

tion has been successful to a large extent (Brown and

Tian, 2002), accurate person-independent pose esti-

mation, which is very crucial for applications like 3D

face modeling, is still in the works.

Current literature (Fu and Huang, 2006)

(Raytchev et al., 2004) (Wenzel and Schiffmann,

2005) separates the existing methods for head pose

estimation into distinct categories:

• Shape-based geometric analysis, where head pose

is discerned from geometric information like the

conﬁguration of facial landmarks.

• Model-based methods, where non-linear paramet-

ric models are derived before using a classiﬁer

like a neural network (Eg. Active Appearance

Models (AAMs)).

• Appearance-based methods, where the pose esti-

mation problem is viewed as a pattern classiﬁca-

tion problem on image feature spaces.

• Template matching approaches, which are largely

based on nearest neighbor classiﬁcation against

texture templates/signatures.

• Dimensionality reduction based approaches,

where linear/non-linear embedding of the face

images is used for pose estimation.

To overcome data redundancy and obtain compact

representations of face images, earlier work (Chen

et al., 2003) (Raytchev et al., 2004) (Fu and Huang,

Nallure Balasubramanian V. and Panchanathan S. (2007).

BIASED MANIFOLD EMBEDDING FOR PERSON-INDEPENDENT HEAD POSE ESTIMATION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 76-82

 SciTePress

2006) suggests to consider the high-dimensional face

image data as a set of geometrically related points

lying on a smooth manifold in the high-dimensional

feature space.

Different poses of the head, although captured in

high-dimensional image feature spaces, can be visual-

ized as data points lying on a low-dimensional man-

ifold in the high-dimensional space. Raytchev et al

(Raytchev et al., 2004) stated that the dimension of

this manifold is equivalent to the number of degrees of

freedom in the movement during data capture. For ex-

ample, images of the human face with different angles

of pose rotation (yaw, tilt and roll) can intrinsically

be conceptualized as a 3D manifold in image fea-

ture space. This conceptualization resulted in a host

of dimensionality reduction techniques that are based

on the relative geometry of the data points in high-

dimensional space. This is the idea that underlies the

family of non-linear dimensionality reduction tech-

niques under the umbrella of manifold learning, like

Isomap, Locally Linear Embedding (LLE), Laplacian

Eigenmaps, Local Tangent Space Alignment (LTSA),

etc, which have become popular in recent times.

In prior work in this domain, (Raytchev et al.,

2004) and (Hu et al., 2005) employed a straightfor-

ward approach to learn the non-linear mapping onto

the low-dimensional space through manifold learning,

and estimated the pose angle using a pose parame-

ter map. In the work carried out so far, the pose in-

formation of the given face images is ignored while

computing the embedding. In this light, we propose

a novel improvement to traditional manifold learn-

ing techniques, called the Biased Manifold Embed-

ding approach, which provides a semantic bias to the

manifold-based embedding process, using pose infor-

mation from the given face image data. While the

proposed Biased Manifold Embedding method is il-

lustrated using Isomap in this paper, it can easily be

extended to other manifold learning techniques with

minor adaptations. As broader impact, the work pro-

posed here is a signiﬁcant contribution to a supervised

approach to manifold-based non-linear dimensional-

ity reduction techniques across all regression prob-

lems.

We discuss the background with a brief descrip-

tion of the Isomap algorithm, followed by related

work and an insight into the signiﬁcance of our work

in Section 2. Section 3 details the mathematical for-

mulation of the proposed Biased Manifold Embed-

ding method. The experimental setup and the method-

ology of our experiments are briefed in Section 4. The

results of the experiments are discussed in Section 5.

We then discuss the advantages and limitations of the

approach in the concluding section in Section 6, and

provide future directions to this work.

2 BACKGROUND

2.1 Non-linear Dimensionality

Reduction Using Isomap

Finding low-dimensional representations of high-

dimensional data is a common problem in science

and engineering. High-dimensional observations

are prevalent in all ﬁelds: images, spectral data,

instrument readings, etc. Techniques like Principal

Component Analysis (PCA) are recognized as linear

dimensionality reduction techniques, because of the

linear projection matrix obtained from the eigen

vectors of the covariance matrix. Techniques like

Multi-Dimensional Scaling (MDS) are grouped un-

der non-linear dimensionality reduction techniques.

However, MDS uses the L2 (Euclidean) distance

between data points in the high-dimensional space

to capture their similarities. If the data points were

to lie on a manifold in the high-dimensional space,

Euclidean distances do not capture the geometric re-

lationship between the data points. In such cases, it is

beneﬁcial to consider the geodesic (along the surface

on which the data points lie) distances between the

data points to obtain a more truthful representation of

the data.

To capture the global geometry of the data points,

Tanenbaum et al (Tanenbaum et al., 2000) proposed

Isomap to compute an isometric low-dimensional

embedding of a given set of high-dimensional data

points (See Algorithm 1).

While Isomap captures the global geometry of the

data points in the high-dimensional space, the dis-

advantage of this family of manifold learning tech-

niques is the lack of a projection matrix to embed out-

of-sample data points after the training phase. This

makes the method more suited for data visualization,

rather than classiﬁcation problems. However, the ad-

vantage of these techniques to capture the relative ge-

ometry of data points enthuses researchers to adopt

this methodology to solve problems like head pose

estimation, where the data is known to possess geo-

metric relationships in a high-dimensional space. Fig-

ure 1 shows the visualization results of using Isomap

to embed face images onto 2 dimensions. Faces of

10 individuals with 11 pose angles (-75

◦

to +75

◦

increments of 15) were used to perform this embed-

ding. The feature space considered here was the space

BIASED MANIFOLD EMBEDDING FOR PERSON-INDEPENDENT HEAD POSE ESTIMATION

learning techniques to treat out-of-sample data points.

There has been recent work by (Ridder et al.,

2003) and (Yu and Tian, 2006) to obtain a supervised

approach to manifold learning techniques. However,

their approaches are strictly oriented towards classi-

ﬁcation problems, and do not exploit the label infor-

mation as possible for regression problems like head

pose estimation.

2.3 Proposed Approach

While manifold learning techniques like Isomap

capture the global geometrical relationship between

data points in the high-dimensional image feature

space, they do not use the pose label information

of the training data samples. Unlike class labels

in classiﬁcation problems, pose information can be

viewed as an ordered single-dimensional label with

an established distance metric. This can provide

valuable input to the embedding process.

In this work, we propose a biased manifold-based

embedding for head pose estimation. We use the

given pose information to bias the non-linear embed-

ding to obtain accurate pose angle estimation. The

signiﬁcance of our contribution is realized in the

fact that the proposed Biased Manifold Embedding

method, although validated in this work with Isomap,

can be extended to other manifold learning techniques

with minor modiﬁcations, and in general, can be ap-

plied to all regression problems that use manifold

learning methods. In addition, while most current ap-

proaches use face images sampled with pose angles

at increments of 10-15

◦

(Raytchev et al., 2004), we

use the FacePix database (Little et al., 2005) that in-

cludes images of faces taken at a wide range of pre-

cisely measured pose angles with a readily available

granularity of 1

◦

. This reinforces the validity of our

experiments with the proposed approach.

3 BIASED MANIFOLD

EMBEDDING

In the Biased Manifold Embedding method, we pro-

pose to use the pose angle information of the training

data samples to obtain a more meaningful embedding

with a view to solve the problem of pose estimation.

The fundamental idea of our approach is that face

images with nearer pose angles must be nearer to

each other in the low-dimensional embedding, and

images with farther pose angles are placed farther,

irrespective of the identity of the individual. We

achieve this with a modiﬁcation to the computation

of the geodesic distance matrix. Since a distance

metric can easily be deﬁned on the pose angle values,

the problem of ﬁnding closeness of pose angles is

straight-forward.

The mathematical formulation of the Biased Man-

ifold Embedding method is given below. We would

like the ideal modiﬁed geodesic distance between a

pair of data points to be of the form:

D(i, j) = f (P(i, j)) ⊗ D(i, j)

where D(i, j) ( = d

in Algorithm 1) is the geodesic

distance between two data points x

and x

D(i, j) is

the modiﬁed biased geodesic distance, P(i, j) is the

pose distance between x

and x

, f is any function of

the pose distance, and ⊗ is a binary operator. If ⊗

was chosen as the multiplication operation, the func-

tion f would be chosen as inversely proportional to

the pose distance, P(i, j). In a more general perspec-

tive, the function f could be picked from the family

of reciprocal functions ( f ∈ F

) based on the needs of

an application. In this work, we choose the function

as:

f (P(i, j)) =

max

m,n

P(m, n) − P(i, j)

This function could be replaced by an inverse expo-

nential or quadratic function of the pose distance. In

order to ensure that the biased geodesic distance val-

ues are well-separated for different pose distances, we

multiply this quantity by a function of the pose dis-

tance:

D(i, j) =

α(P(i, j))

max

m,n

P(m, n) − P(i, j)

∗ D(i, j)

where the function a is directly proportional to the

pose distance, P(i, j), and is deﬁned in our work as:

α(P(i, j)) = β ∗ |P(i, j)|

where β is a constant of proportionality, and allows

parametric variation for performance tuning. In our

work, we have used the pose distance as the one-

dimensional distance i.e. P(i, j) = |Pi − P j|, where

is the pose angle of x

. In summary, the biased

geodesic distance between a pair of points can be

given by:

D(i, j) =

(

α(P(i, j))

max

m,n

P(m,n)−P(i, j)

∗ D(i, j) P(i, j) 6= 0,

0 P(i, j) = 0.

(1)

Classical MDS is applied on this biased geodesic

distance matrix to obtain the embedding. The pro-

posed modiﬁcation impacts only the computation of

the geodesic distance matrix, and hence, can easily

BIASED MANIFOLD EMBEDDING FOR PERSON-INDEPENDENT HEAD POSE ESTIMATION

be extended to other manifold-based dimensionality

reduction techniques that use the geodesic distance.

Figure 2 shows the results of using Biased Isomap

to embed the same facial images used in Figure 1 onto

2 dimensions. The embedded images establish the

tendency of the method to elicit person-independent

representations of the pose angles of the given fa-

cial images. As expected from the formulation of the

method (see Figure 2), the face images of all individ-

uals with the same pose angle have merged onto the

same data point in 2 dimensions. This renders an em-

bedding that is more conducive to determine the pose

angle from the face images.

(a) Biased Isomap embedding with 10 neighbors

(b) Biased Isomap embedding with 20 neighbors

Figure 2: Biased Isomap Embedding of face images with

varying poses onto 2 dimensions. Note in 2(b) that all the

face images w ith the same pose angle have merged onto the

same 2D point.

4 EXPERIMENTAL SETUP AND

METHODOLOGY

The proposed Biased Isomap Embedding approach

was compared against the traditional Isomap method

for non-linear dimensionality reduction in the head

pose angle estimation process. We used the FacePix

face database (Little et al., 2005) (see Figure 3) built

at the Center for Cognitive Ubiquitous Computing

(CUbiC), which has face images with precisely mea-

sured pose variation. In this work, we consider a

set of 2184 face images, consisting of 24 individuals

with pose angles varying from -90

◦

to +90

◦

in incre-

ments of 2

◦

. The images were subsampled to 32 x

32 resolution, and different feature spaces of the im-

ages were considered for the experiments. The results

presented here include the grayscale pixel intensity

feature space and the Laplacian of Gaussian (LoG)

transformed image feature space (see Figure 4). The

LoG transform was used since pose variation in face

images is a result of geometric transformation, and

texture information may not be really useful for the

pose estimation problem. This was also reﬂected in

preliminary experiments conducted with Gabor ﬁlters

and Fourier-Mellin transformed images. The images

were subsequently rasterized and normalized.

Figure 3: The data capture setup for FacePix.

(a) Grayscale im-

age

(b) Laplacian of

Gaussian (LoG)

tranformed image

Figure 4: Image feature spaces used for the experiments.

Non-linear dimensionality reduction techniques

like manifold learning do not provide a projection

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

matrix to handle test data points. While different

approaches have been used by earlier researchers

to capture the mapping from the high-dimensional

feature space to the low-dimensional embedding, we

adopted a Generalized Regression Neural Network

(GRNN) with Radial Basis Functions to learn the

non-linear mapping. This approach has been adopted

earlier by Zhao et al (Zhao et al., 2005). Additionally,

the parameters involved in training the network (just

the spread of the Radial Basis Function) are minimal,

thereby facilitating better evaluation of the proposed

method. Once the low-dimensional embedding was

obtained, linear multi-variate regression was used to

obtain the pose angle of the test image.

The proposed Biased Isomap Embedding method

was compared with the traditional Isomap approach

using resubstitution and 8-fold cross-validation mod-

els. In the resubstitution model, 100 data points were

randomly chosen from the training sample for the

testing phase. The error in estimation of the pose an-

gle was used as the metric for performance evaluation.

In the 8-fold cross-validation model, face images of

3 individuals were used for the testing phase in each

fold, while all the remaining images were used in the

training phase. In addition to these experiments, the

variation in accuracy of the proposed method with the

embedding dimension and the number of neighbors

for the embedding was studied.

5 RESULTS AND DISCUSSION

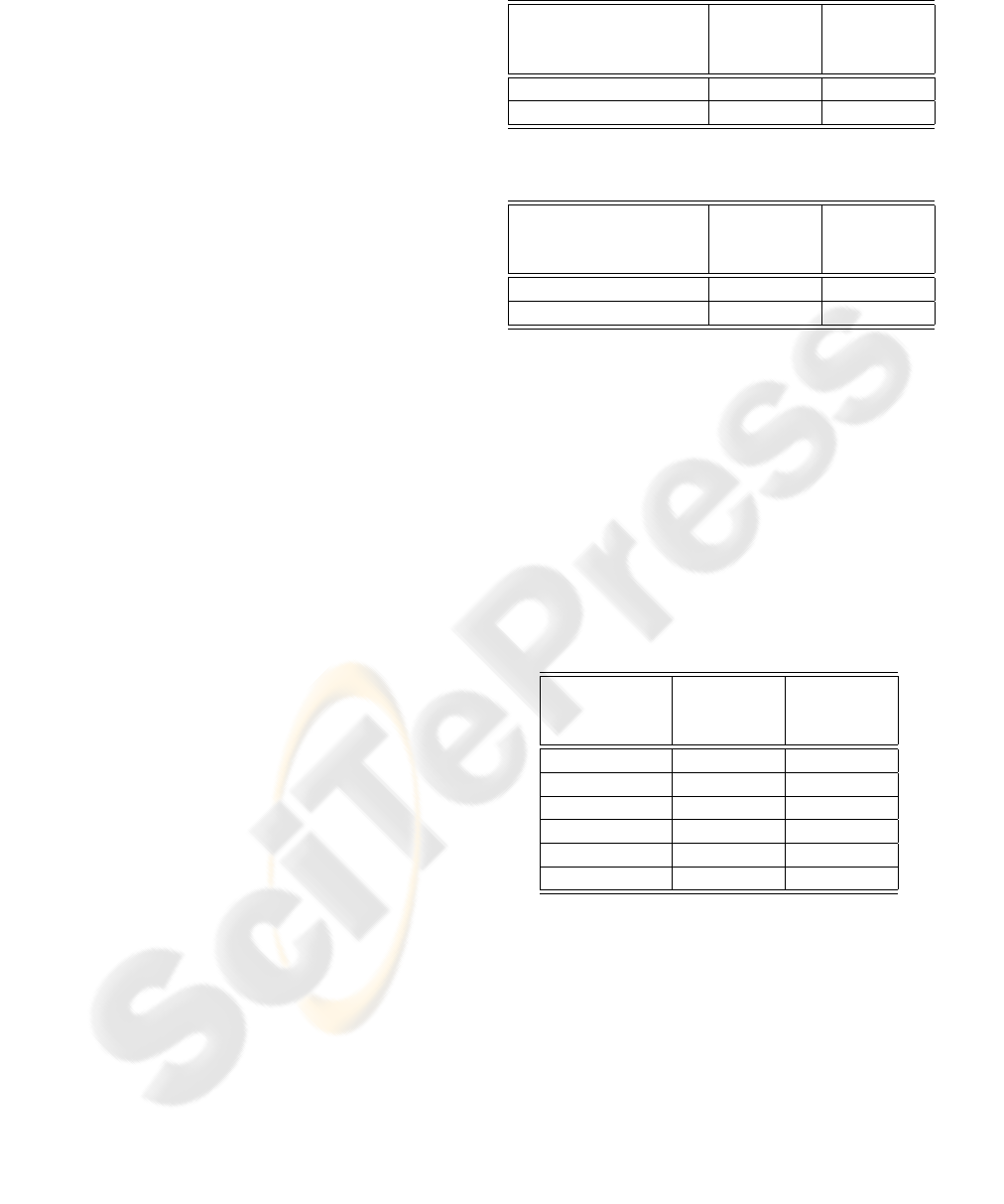
The results for the resubstitution model are presented

in Table 1. The improved performance of the Biased

Isomap Embedding method for head pose estimation

is unanimously reﬂected in the signiﬁcant reduction

in error values across the image feature spaces. How-

ever, validation using the resubstitution model is pre-

liminary since test samples are picked from the train-

ing sample set itself. For more robust validation, we

implemented 8-fold cross-validation over the images

from 24 individuals. The results of these experiments

are shown in Table 2. The results with the cross-

validation model corroborate our claim of the perfor-

mance gain. Both of these experiments were carried

out with an embedding dimension of 8, with a choice

of 50 neighbors for the embedding. The pose an-

gle estimate error is consistently under 4

◦

, which is a

substantial improvement over earlier work (Raytchev

et al., 2004).

In addition, the performance of the Biased Man-

ifold Embedding was analyzed with varying dimen-

Table 1: Results using the resubstitution model.

Feature Space Error using Error using

traditional Biased

Isomap Isomap

Grayscale 11.39 1.98

Laplacian of Gaussian 8.80 2.31

Table 2: Results using the 8-fold cross-validation model.

Feature Space Error using Error using

traditional Biased

Isomap Isomap

Grayscale 10.55 3.68

Laplacian of Gaussian 9.10 3.38

sions of embedding, and choice of the number of

neighbors used for embedding. Table 3 captures the

results for different embedding dimensions with the

number of neighbors ﬁxed at 50. Table 4 captures

the results for varying number of neighbors for the

embedding with the embedding dimension ﬁxed at 8.

Grayscale pixel intensities of the face images were

used for these independent experiments.

Table 3: Analysis of performance with varying dimensions

of embedding.

Dimension of Error using Error using

Embedding traditional Biased

Isomap Isomap

100 10.41 5.02

50 10.86 5.04

20 11.35 5.04

8 12.96 5.07

5 12.57 5.05

3 16.21 5.66

As evident from the results, the signiﬁcant reduc-

tion in the error of estimation of pose angle substan-

tiates the effectivness of the proposed approach. In

addition, as the results in Tables 2, 3 and 4 illustrate,

the Biased Manifold Embedding method is robust to

variations in feature spaces, dimensions of embedding

and choice of number of neighbors. While the tradi-

tional Isomap embedding has ﬂuctuating results for

these parameters, the range of error values obtained

for the Biased Manifold Embedding method across

these parameter changes suggests the high stability of

the method, thanks to the biasing of the embedding.

BIASED MANIFOLD EMBEDDING FOR PERSON-INDEPENDENT HEAD POSE ESTIMATION

Table 4: Analysis of performance with varying number of

neighbors for embedding.

Number of Error using Error using

Neighbors traditional Biased

Isomap Isomap

30 11.56 5.10

50 12.96 5.06

100 13.83 5.03

200 12.59 5.06

500 14.36 5.07

6 CONCLUSION

We have proposed the Biased Manifold Embedding

method, a novel supervised approach to manifold

learning techniques for regression problems. The

proposed method was validated for accurate person-

independent head pose estimation. The use of pose

information in the manifold embedding process im-

proved the performance of the pose estimation pro-

cess signiﬁcantly. The pose angle estimates obtained

using this method are accurate, and can be relied upon

with an error margin of 3-4

◦

. Our experiments also

demonstrated that the method is robust to variations in

feature spaces, dimensionality of embedding and the

choice of the number of neighbors for the embedding.

The proposed method can easily be extended from the

current Isomap implementation to cover the envelop

of other manifold learning techniques, and can be de-

veloped as a framework for biased manifold learning

to cater to all regression problems at large.

6.1 Limitations and Future Work

As mentioned earlier, a signiﬁcant drawback of man-

ifold learning techniques is the lack of a projection

matrix to treat new data points. While we used the

GRNN to learn the non-linear mapping in this work,

there have been other approaches adopted by various

researchers. Bengio et al (Bengio et al., 2004) pro-

posed a mathematical formulation focussed to over-

come this problem. We plan to use these approaches

to support the validity of our approach. Besides, we

intend to extend the Biased Manifold Embedding im-

plementation to LLE and Laplacian Eigenmaps to es-

tablish it as a framework for non-linear dimensional-

ity reduction in regression applications. On a lesser

signiﬁcant note, another limitation of the current ap-

proach is that the number of neighbors chosen to ob-

tain the embeddding has to be more than the num-

ber of individuals in the face images. This is because

different individuals with the same pose angle are as-

signed a zero distance value in the biased geodesic

distance matrix. We plan to modify our algorithm to

overcome this limitation. In addition, the function of

pose distance used to bias the geodesic distance ma-

trix can be varied to study the applicability of different

reciprocal functions for pose estimation.

REFERENCES

Bengio, Y., Paiement, J. F., Vincent, P., and Delalleau, O.

(2004). Out-of-sample extensions for lle, isomap,

mds, eigenmaps, and spectral clustering.

Brown, L. and Tian, Y.-L. (2002). Comparative study of

coarse head pose estimation.

Chen, L., Zhang, L., Hu, Y. X., Li, M. J., and Zhang, H. J.

(2003). Head pose estimation using ﬁsher manifold

learning. In IEEE International Workshop on Analy-

sis and Modeling of Faces and Gestures (AMFG03),

pages 203–207, Nice, France.

Fu, Y. and Huang, T. S. (2006). Graph embedded analysis

for head pose estimation. In 7th International Con-

ference on Automatic Face and Gesture Recognition,

Southampton, UK.

Hu, N., Huang, W., and Ranganath, S. (2005). Head pose

estimation by non-linear embedding and mapping. In

IEEE International Conference on Image Processing,

page 342345, Genova.

Little, G., Krishna, S., Black, J., and Panchanathan, S.

(2005). A methodology for evaluating robustness

of face recognition algorithms with respect to vari-

ations in pose and illumination angle. In Proceed-

ings of IEEE International Conference on Acoustics,

Speech and Signal Processing, page 8992, Philadel-

phia, USA.

Raytchev, B., Yoda, I., and Sakaue, K. (2004). Head

pose estimation by nonlinear manifold learning. In

17th International Conference on Pattern Recognition

(ICPR04), Cambridge, UK.

Ridder, D. d., Kouropteva, O., Okun, O., Pietikainen, M.,

and Duin, R. P. (2003). Supervised locally linear em-

bedding. In International Conference on Artiﬁcial

Neural Networks and Neural Information Processing,

333341.

Tanenbaum, J. B., Silva, V. d., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science, 290(5500):23192323.

Wenzel, M. T. and Schiffmann, W. H. (2005). Head pose

estimation of partially occluded faces. In Second

Canadian Conference on Computer and Robot Vision

(CRV05), page 353360, Victoria, Canada.

Yu, J. and Tian, Q. (2006). Learning image manifolds by

semantic subspace projection. In ACM Multimedia,

Santa Barbara, CA, USA.

Zhao, Q., Zhang, D., and Lu, H. (2005). Supervised lle in

ica space for facial expression recognition. In Interna-

tional Conference on Neural Networks and Brain (IC-

NNB05), volume 3, page 19701975, Beijing, China.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications