DETECTING COPLANAR FEATURE POINTS IN HANDHELD

IMAGE SEQUENCES

Olaf K¨ahler and Joachim Denzler

Department of Mathematics and Computer Science, Friedrich-Schiller-University, Jena, Germany

Keywords:

Planar patches, homography, degenerate motion.

Abstract:

3D reconstruction applications can beneﬁt greatly from knowledge about coplanar feature points. Extracting

this knowledge from images alone is a difﬁcult task, however. The typical approach to this problem is to search

for homographies in a set of point correspondences using the RANSAC algorithm. In this work we focus on

two open issues with a blind random search. First, we enforce the detected planes to represent physically

present scene planes. Second, we propose methods to identify cases, in which a homography does not imply

coplanarity of feature points. Experiments are performed to show applicability of the presented plane detection

algorithms to handheld image sequences.

1 INTRODUCTION

Planar structures are abundant in man-made environ-

ments and impose strong geometric constraints for the

points on them. They have caught the interest of re-

search before, and a typical application is the repre-

sentation of video data as independent layers (Baker

et al., 1998; Odone et al., 2002) or the interpretation

of 3D scene structure (Gorges et al., 2004). Also, for

geometric reconstruction tasks, planar structures play

an important role. E.g. incorporation of the copla-

narity constraints into a point based reconstruction al-

gorithm has been explored (Bartoli and Sturm, 2003)

and computing 3D planes from 2D homographies is

possible (Rother, 2003). To beneﬁt from coplanarity

in 3D reconstruction, it is necessary to detect the pla-

nar structures from 2D information alone.

A central concept for the identiﬁcation of copla-

nar features in image sequences is the plane induced

homography (Baker et al., 1998). Planar regions are

mapped from one image of the sequence to another by

a 2D-2D projective mapping, also called collineation

or homography. This key idea has been used before

to search for dominant homographies in a set of point

correspondences using random sampling consensus

and related techniques (Odone et al., 2002; Lourakis

et al., 2002; Gorges et al., 2004; K¨ahler and Denzler,

2006). While the mentioned works purely rely on a

sparse set of correspondences, other, computationally

more intensive methods concentrate on an accurate

segmentation and delineation of the planes using re-

gion growing algorithms and dense matching (Fraun-

dorfer et al., 2006). Our work is settled among the

fast, actually real-time algorithms using only sparse

correspondences. The addressed problems, however,

are inherent to the usage of homographies in general,

independent of the method actually used.

While a homography might cover coplanarity in

a geometrical sense, the actually interesting, phys-

ically present scene planes are only a small subset

of all possibly coplanar point sets. A blind search

as in RANSAC will therefore detect spurious, “vir-

tual” planes, which was also recognized in previous

research (Gorges et al., 2004). We present a more rig-

orous analysis of the problem in section 3, leading to

a theoretically justiﬁed side condition in plane search.

Although the homography is a necessary criterion

for planar regions, it is not a sufﬁcient one (K¨ahler

and Denzler, 2006). To give a very simple example,

all points are mapped by a common homography, the

identity, between two images of a static camera. Yet

not all the points need to be on one plane. Copla-

narity of points can only be detected, if the optical

center has moved between two images. As cases with

a static or a purely rotating camera are abundant in

handheld image sequences, zero camera translations

have to be identiﬁed automatically and a detection of

false planes has to be prevented then. In section 4,

we outline the analysis of (K¨ahler and Denzler, 2006)

and extend it by model selection criteria (Torr et al.,

447

Kähler O. and Denzler J. (2007).

DETECTING COPLANAR FEATURE POINTS IN HANDHELD IMAGE SEQUENCES.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 447-452

 SciTePress

1999). An experimental performance evaluation and

comparison of the approaches is provided in section 5.

2 DETECTING PLANES

To detect planar regions in an image sequence, at

ﬁrst point correspondences are established between

two images of the sequence. In this work, we use

KLT-tracking (Shi and Tomasi, 1994), which seems

appropriate for e.g. 30 frames/sec and typical mo-

tion speeds of handheld cameras. For plane detection,

we analyze the motion of the points between two, not

necessarily successive frames.

The key idea for detection of coplanarity then is to

ﬁnd homographies. It is well known that planar scene

areas observed in two different views with a perspec-

tive camera are related to each other by a homogra-

phy. Hence we can deﬁne the task of detecting a pla-

nar patch as ﬁnding “a set of points that is transferred

between two images by a common homography”.

2.1 Basic Ransac

In the task of ﬁnding planes, it is intuitive to take

care of points off the plane. If ﬁnding the plane in-

duced homography is considered an estimation prob-

lem, the points off the plane are outliers and meth-

ods of robust estimation can be applied. In particu-

lar the RANSAC approach seems to be the method of

choice for this problem, and it was also used in previ-

ous works (Gorges et al., 2004; Lourakis et al., 2002).

The RANSAC approach generates hypotheses by

selecting a minimum number of random points, such

that a homography can be estimated. These are typi-

cally four points with no three of them being collinear.

Approaches with three points are possible, but require

additional constraints like known epipolar geome-

try (Lourakis et al., 2002) and are not used here.

Once the homography induced by the hypothe-

sis is computed, the point correspondences supporting

this hypothesis can be counted. The supporting points

are those correctly transferred by the homography up

to e.g. 2 pixels accuracy. Many hypotheses are gener-

ated and in the end the homography supported by the

largest number of point correspondences is kept. This

is called the dominant homography or plane (Odone

et al., 2002; Gorges et al., 2004).

2.2 Iterative Dominant Homography

It is straight forward to extend this in order to get a

decomposition of all the observed point correspon-

dences into several homographies, or a decomposi-

tion of the set of points into planes. Once a domi-

nant homography is found, the points supporting it are

removed and another dominant homography is com-

puted for the remaining points. This is iterated until

no more homographies can be established.

3 PLANES TO AVOID

Up to now, a blind search is employed to detect all

kinds of coplanar points. This can not be enough to

identify physically present scene planes, as is shown

in ﬁgure 1. “Virtual” planes are detected there. These

do actually consist of coplanar points, but the geomet-

ric plane containing the points does not correspond to

any physical plane in the scene. With the purely geo-

metric deﬁnition of coplanarity used so far, it is not

possible to distinguish “virtual” planes from physical

scene planes.

On ﬁrst sight, the points on virtual planes seem

to be distributed along two lines, as in ﬁgure 1. But

as the virtual plane intersects a third or fourth physi-

cal scene plane, a third or fourth line distribution will

result. On a closer look, the physical planes we are in-

terested in are contiguous 2D entities in 3D space, and

as such they are mapped to contiguous 2D areas in the

observed images. The deﬁnition of a planar patch is

hence extended to “a set of points in a closed region

that is transferred between two images by a common

homography”. This enforces validity of the homogra-

phy for the whole closed region, and not only at some

of its outlines.

Various strategies can be used to implement this

deﬁnition algorithmically. Constructing a dense set

of matches while using region growing might be one

solution (Fraundorfer et al., 2006). The closed re-

gion constraint is then directly enforced by the re-

gion growing algorithm. Working only on a sparse

set of correspondences, the problem was approached

by picking the four seed points of RANSAC in a local

neighborhood (Gorges et al., 2004). Thus it is likely

to compute the homography of a physical plane, and

Figure 1: Detection of a “virtual” plane, that contains copla-

nar points but does not correspond to any physical plane.

that all other points conforming the homography are

on the same physical plane.

The idea used in this work is to pick all point cor-

respondences in a closed area of the image as seed

points. This is achieved by starting from one random

point and then iteratively adding the closest known

point correspondences, until a homography can be

computed. Approaching a dense set of correspon-

dences, it is more and more certain that the detected

planes correspond to physical scene planes.

4 NO CAMERA TRANSLATION

The use of homographies introduces another problem

to plane detection. Homographies are a necessary cri-

terion for coplanarity, but not a sufﬁcient one. In case

of a camera rotation or zoom without a translation of

the optical center, no information on coplanarity can

be inferred. This can also be derived from the follow-

ing standard decomposition of a homography H:

H = αK

(R+

−1

(1)

where K

and K

are the intrinsic camera matrices, R

and t are the relative motion and n and d are the plane

normal its distance from the origin.

If and only if t = 0, a difference in plane normals

n does not inﬂuence the homography H. We hence

extend the deﬁnition of a planar patch to “a set of

points in a closed region that is transferred by a com-

mon homography in case of non-zero camera trans-

lation”. Several methods were proposed to identify a

non-zero camera translation (Torr et al., 1999; K¨ahler

and Denzler, 2006). A short overview of the different

approaches is given in the following, in order to show

applicability to our problem and motivate the experi-

mental comparison performed in section 5.

4.1 Homography Decomposition

A ﬁrst idea is to analyze a single homography matrix

and check for both the terms of the decomposition (1).

The term tn

is not present if there was no camera

translation t = 0 or if the homography was induced by

the plane at inﬁnity n = 0. Although these two cases

can not be disambiguated, using only knowledge of

a single homography allows to handle independently

moving scene planes, which will not be the case for

the methods presented later on.

In the simplest case, the intrinsic camera matrices

and K

are known. The matrix H

′

then expresses

the homography in camera coordinates:

′

= K

−1

= α(R+

)

If and only if t= 0 or n = 0, H

′

is a scaled rotation ma-

trix αR, and all singular values of H

′

are equal. Test-

ing for a translational part in H can hence be achieved

by computing the ratio of largest to smallest singular

value of H

′

, which will be 1 for t = 0.

Frequently the intrinsic camera parameters are un-

known, but known to be constant. In such cases a

slightly different analysis of H can be used. The ma-

trices H and H

′

will be related by a similarity relation,

i.e. they will have the same determinant, eigenvalues

and some more properties, which can be found in any

linear algebra textbook. Again if t = 0 then H

′

is a

scaled rotation matrix, all eigenvalues of H will have

the same absolute value, and the ratio of largest to

smallest absolute eigenvalue will be 1. This is not a

two way implication, as was pointed out in (Torr et al.,

1999). In the case of n

t = 0, the triple absolute

eigenvalue of 1 will follow for arbitrary t.

For both criteria, small deviations from the ratio of

1 can be allowed to cope with noisy correspondences

and inaccurate homographies. An experimental eval-

uation of the detection rate vs. false alarms with dif-

ferent thresholds is given in section 5.2.

4.2 Global Homography

If no knowledge about the intrinsic parameters is

available, analyzing on-plane information for a single

homography matrix can not be sufﬁcient for deciding,

whether a camera translation was present or not. E.g.

with a QR-decomposition, any homography matrix H

can be decomposed into a rotation R and an upper tri-

angular matrix K

. The term tn

from equation (1) is

not necessary. Using off-plane information however,

a static scene has to be assumed.

An intuitive idea is to check, whether all observed

points conform with the same homography (Fraun-

dorfer et al., 2006). In cases with just one scene plane

visible, such a test will fail. The only other cases with

a global homography are a pure rotation and change

of intrinsics without translation.

Hence, if the dominant homography from sec-

tion 2.2 is valid for almost all points, we can as-

sume that no camera translation was present. A small

amount of outliers should be tolerated, however, to

handle incorrect point correspondences. As before,

this introduces an adjustable threshold and a trade-off

between detection and false alarm rates. An experi-

mental evaluation is given in section 5.2.

4.3 Model Selection

Detecting degenerate camera motions without adjust-

ing thresholds would be an appealing alternative. We

will therefore investigate statistical model selection

approaches in this context (Torr et al., 1999; Kanatani,

2004). The basic idea is to select, whether the global

homography or the epipolar geometry model is better

suited to explain the observed point correspondences.

In a sense, this is the global homography criterion

of above with the threshold determined automatically,

depending on the performance of epipolar geometry.

Hence these methods can also be used in case of un-

known intrinsic parameters and they will also fail in

case of only one plane visible.

To apply model selection, ﬁrst the two models are

instantiated with the respective optimal parameters.

The most dominant homographyis used as before and

the epipolar geometry is established using RANSAC

and the normalized 8-Point-Algorithm. The residuals

(M)

for point i ∈ [1. . . N] using model M can then be

computed. It is not sufﬁcient to compare these residu-

als, as models with more degrees of freedom will usu-

ally adapt better to the observed data. The costs for

using model M have to be considered, and the task is

to select

M explaining the correspondences with least

residuals and least number of parameters k

(M)

To handle constraints of different dimensionality,

geometric model selection criteria have been devel-

oped (Kanatani, 2004; Torr, 1997). As a key, the i-th

point correspondence has to be considered as a vec-

tor (x

, y

, x

′

, y

′

) with D = 4 degrees of freedom. The

homography model constraints a point (x

, y

) onto a

corresponding point (x

′

, y

′

), and hence is a model of

dimension d

(H)

= 2. The epipolar geometry in con-

trast restricts a point only onto a corresponding epipo-

lar line, and as a third parameter is needed to deﬁne

the whole correspondence, this is a model of dimen-

sion d

(F)

= 3. The residuals can only be measured

in the dimensions actually constrained by the model.

To compensate for these different residual measure-

ments, the degrees of freedom in the correspondences

(M)

have to inﬂuence the overall costs as well.

Further the noise disturbing the point correspon-

dences has to be known in order to establish a relation

between the residuals ε

(M)

, the number of parameters

(M)

and the dimensionality d

(M)

of a model. If an

isotropic normal distribution is assumed, the standard

deviation σ can be estimated as the expected residual

of the most general model F (Kanatani, 2004):

∑

i=1

∗



D− d

∗

)



N − k

∗

)

Now the cost of a model is a weighted sum of all

the mentioned contributions, and the model with least

cost is selected. Different weightings have been pro-

Table 1: Various values for γ

and γ

found in model selec-

tion literature.

Name γ

GAIC (Kanatani, 2004) 2 2

GBIC1 (Torr, 1997) 2 2lnN

GBIC2 (Torr et al., 1999) ln4 ln(4N)

GMDL (Kanatani, 2004) −ln

−ln

posed, however. They can be summarized as:

Cost(M) =

∑

i=1

(M)2

+ γ

(M)

N + γ

(M)

(2)

with γ

and γ

from table 1. In the GMDL criterion,

the image size S is explicitly used to avoid inﬂuences

from different scalings.

These methods are easily applied to our problem

of identifying camera translation. If the homogra-

phy is a “cheaper” model than the epipolar geometry,

in the sense of ﬁtting the observed correspondences

comparably accurate but with fewer degrees of free-

dom, we assume a zero camera translation was re-

sponsible for that global homography. In section 5.2,

the performance of different γ

and γ

will be com-

pared to each other and to the thresholded criteria.

5 EXPERIMENTS

Our proposed methods directly tackle the mentioned

problems of plane detection, and hence allow the

detection of coplanarity in a much wider range of

scenarios. To demonstrate the overall performance

in practical applications, we present an experimental

evaluation of the algorithms. First, the basic setup

of the experiments and qualitative results are shown,

then in section 5.2 the methods for detection of cam-

era translation are compared.

5.1 Qualitative Evaluation

For the evaluation, two types of scene setups were

used. The ﬁrst of them can be considered rather ar-

tiﬁcial, showing an ofﬁce environment with checker-

board patterns placed in the scene. These patterns

are used only to provide good features for the point

tracker, they are not needed in the further processing

steps. The second set is made up from architectural

scenes of model buildings.

Examples from the sequences with detected

planes are shown in ﬁgures 2 and 3. Note that for vi-

sualization, a convex hull of the coplanar points was

computed. Not all the pixels within these polygons

satisfy the coplanarity constraints, as can be seen e.g.

Figure 2: Excerpts of a calibration pattern scene with planar patches detected in the individual frames shown as polygons with

thick boundary lines.

Figure 3: Excerpts of an architectural scene with the polygons delineating planar patches found from point correspondences.

at the chimneys on top of the roof in ﬁgure 3. Also,

ﬁnding the exact delineations of the planes is beyond

the scope of this work. Provided only information

at the sparse feature points however, the results are

fairly accurate, and especially the detected planes cor-

respond to physical scene planes.

5.2 Detecting Cases Without

Translation

While for the plane detection itself, a ground-truth

based analysis is hardly possible, the detection of

camera translation can be evaluated accurately. Using

a motorized zoom and a tripod, image sequences were

recorded with purely rotating, zooming and generally

moving camera. These motion classes were labeled

by hand, allowing a comparison of the algorithms’

performance with ground truth data.

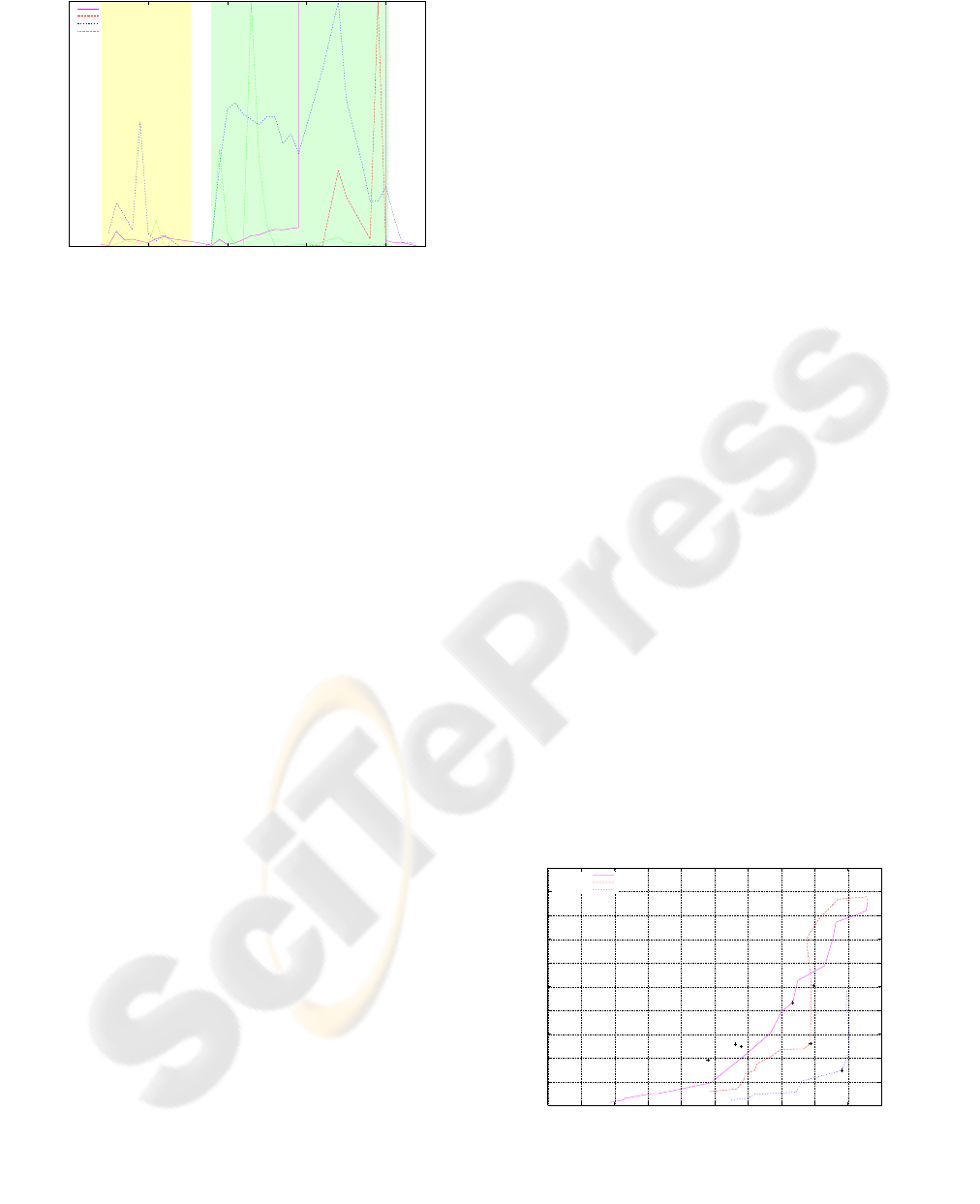
The sample graph in ﬁgure 4 shows the conﬁdence

of various criteria in a translational motion over the

frames of an image sequence. Note the cases with

static camera are clearly identiﬁed by all criteria. Also

the higher peaks in the frames with general motion

allow to identify the camera translation.

Several of the criteria need a threshold for decid-

ing the type of camera motion. As usual, this leads to

a tradeoff between sensitivity and speciﬁcity, which

is illustrated in a ROC-curve in ﬁgure 5. Also the

detection vs. false alarm rate of the model selection

criteria is shown for comparison. In this evaluation,

the frames with zooming cameras were ignored, as

they can not be handled by the singular and eigen-

value criteria. The other methods work equally well

for identiﬁcation of purely zooming cameras.

The global homographycriterion seems to outper-

form the others for a wide range of thresholds. If no

static scene can be assumed and one of the homog-

raphy decomposition approaches is used, the eigen-

value criterion seems to be the best choice. The model

selection criteria GAIC and GBIC1, differing only

slightly in the choice of γ

, show almost exactly the

same performance.

Reasonable thresholds were marked for the crite-

ria requiring one. For the global homography crite-

rion, 12% of outliers are tolerated, for the homogra-

phy decomposition based criteria, a ratio of largest to

smallest singular or eigenvalue of less than 1.17 was

a good indicator for a pure rotation matrix.

6 CONCLUSIONS

Searching for homographies in point correspondences

is a simple, but effectivemethod of detecting coplanar

feature points. As a novelty, we presented an analysis

of situations, where the blind search or even where a

0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame 0 50 100 150 200

confidence in translation

frame

singular

eigenenval

global

GMDL

Figure 4: Conﬁdence of different criteria in a camera trans-

lation. White background indicates static camera, yellow

background a pure rotation and green background a general

motion including translation.

homography does not sufﬁce to identify planes. First

we enforced that the purely geometric homographies

represent physical scene planes, then the case of a

global homography resulting from zero camera trans-

lation was analyzed. Finally, the overall effectiveness

of plane detection was shown in experiments.

Deﬁning coplanarity only via the geometric trans-

fer function of a homography, it is not possible to de-

cide, whether a plane is only geometrically present or

corresponding to a physical scene plane. The key idea

was to use points in a closed image area for the def-

inition of planar patches, as the contiguous 3D plane

surfaces have to be mapped to contiguous 2D areas.

Finally, planes can not be detected in every sit-

uation. If there was no camera translation between

two frames and the optical centers are identical, no

information on coplanarity can be gained. Demand-

ing validity of the detected homographies for frames

with non-zero camera translation allows to handle this

degeneracy. An automatic classiﬁcation of the camera

motion allows the detection of coplanar feature points

also in handheld image sequences.

REFERENCES

Baker, S., Szeliski, R., and Anandan, P. (1998). A layered

approach to stereo reconstruction. In Proc. Computer

Vision and Pattern Recognition, pages 434–441, Santa

Barbara, CA.

Bartoli, A. and Sturm, P. (2003). Constrained structure and

motion from multiple uncalibrated views of a piece-

wise planar scene. International Journal of Computer

Vision, 52(1):45–64.

Fraundorfer, F., Schindler, K., and Bischof, H. (2006).

Piecewise planar scene reconstruction from sparse

correspondences. Image and Vision Computing,

24(4):395–406.

Gorges, N., Hanheide, M., Christmas, W., Bauckhage, C.,

Sagerer, G., and Kittler, J. (2004). Mosaics from arbi-

trary stereo video sequences. In Proc. 26th DAGM

Symposium, pages 342–349, Heidelberg, Germany.

Springer-Verlag.

K¨ahler, O. and Denzler, J. (2006). Detection of planar

patches in handheld image sequences. In Proceedings

Photogrammetric Computer Vision 2006, volume 36

of International Archives of the Photogrammetry, Re-

mote Sensing and Spatial Information Sciences, pages

37–42.

Kanatani, K. (2004). Uncertainty modeling and model

selection for geometric inference. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

26(10):1307–1319.

Lourakis, M., Argyros, A. A., and Orphanoudakis, S. C.

(2002). Detecting planes in an uncalibrated image

pair. In Proc. British Machine Vision Conference

(BMVC2002), pages 587–596.

Odone, F., Fusiello, A., and Trucco, E. (2002). Layered

representation of a video shot with mosaicing. Pattern

Analysis and Applications, 5(3):296–305.

Rother, C. (2003). Linear multi-view reconstruction of

points, lines, planes and cameras using a reference

plane. In Proceedings ICCV 2003, pages 1210–1217,

Nice, France.

Shi, J. and Tomasi, C. (1994). Good features to track.

In IEEE Conference on Computer Vision and Pattern

Recognition CVPR, pages 593–600.

Torr, P. H., Fitzgibbon, A., and Zisserman, A. (1999). The

problem of degeneracy in structure and motion recov-

ery from uncalibrated image sequences. International

Journal of Computer Vision, 32(1):27–45.

Torr, P. H. S. (1997). An assessment of information criteria

for motion model selection. In IEEE Conference on

Computer Vision and Pattern Recognition, pages 47–

53.

100

0 10 20 30 40 50 60 70 80 90 100

false detections

detected translations

GAIC

GBIC1

GBIC2

GMDL

0.12

1.17

singular

eigenval

global

Figure 5: ROC-curve for different methods of detecting

camera translation. An optimal method had 100% of de-

tected translations with 0% of false detections, which is sit-

uated in the lower right corner.