RELIABLE DETECTION OF CAMERA MOTION BASED ON
WEIGHTED OPTICAL FLOW FITTING
Rodrigo Minetto, Neucimar J. Leite
Institute of Computing, State University of Campinas, Campinas, SP, Brazil
Jorge Stolfi
Institute of Computing, State University of Campinas, Campinas, SP, Brazil
Keywords:
Camera motion, video segmentation, optical flow, least-squares fitting, KLT algorithm.
Abstract:
Our goal in this paper is the reliable detection of camera motion (pan/zoom/tilt) in video records. We propose
an algorithm based on weighted optical flow least-square fitting, where an iterative procedure is used to im-
prove the corresponding weights. To the optical flow computation we used the Kanade-Lucas-Tomasi feature
tracker. Besides detecting camera motion, our algorithm provides a precise and reliable quantitative analysis
of the movements. It also provides a rough segmentation of each frame into “foreground” and “background”
regions, corresponding to the moving and stationary parts of the scene, respectively. Tests with two real videos
show that the algorithm is fast and efficient, even in the presence of large objects movements.
1 INTRODUCTION
Our goal in this work is the reliable detection of
camera motion in video images. This detection is
closely related, for example, to the topic of content-
based video retrieval in which the camera motion in-
formation is used for structural segmentation and in-
dexing of video databases. Usually, a video con-
sists of many continuous parts, called shots, separated
by abrupt cuts or gradual transitions (like fades, dis-
solves, wipes, etc). The problem of detecting such
editing transitions and segmenting a video into shots
has received much attention in recent years. How-
ever, due to the various camera motion inside a shot,
this level of segmentation is often insufficient, e.g. for
choosing key-frames for each video segment. Our mo-
tion detection algorithm can be used to provide this
second level of segmentation and improve the video
abstraction in an indexing process.
This work deals with a camera in a fixed location
exhibiting three degrees of freedom — pan (left or
right), tilt (up or down), and zoom (in or out).
In tests with real videos, our approach reported
about 95% of the frame pairs where camera motion
occurred, and about 98% of these frames did have
camera motion. Besides detecting camera motion, our
method also provides a precise and reliable quantita-
tive analysis of the movements — namely, the amount
of pan, tilt and zoom between any two consecutive
frames. It also provides a rough segmentation of each
frame into “foreground” and “background” regions,
corresponding to the moving and stationary parts of
the scene.
Our method consists of two main steps applied to
each pair of consecutive frames. The first step deter-
mines the optical flow field which can be interpreted
as the velocity of the scene “flowing” throught each
pixel. Then, the second step estimates the camera mo-
tion from the obtained optical flow field.
For the first step, we propose to use the
Kanade-Lucas-Tomasi feature tracking algorithm
(KLT) (Tomasi and Kanade, 1991), which derives
from the work of Lucas and Kanade (Lucas and
Kanade, 1981).
The second step considers a weighted least-
squares matching in the decomposition of the optical
flow field into the sum of four component fields. The
first three are the fields expected from camera move-
ments (pan, tilt, and zoom). The fourth is a residual
“error” field that is assumed to be due to events such
as scene motion, video quantization, etc.
This paper is organized as follows. The next sec-
tion describes previous works on camera motion de-
tection. Section 3 and 4 describe our algorithm in de-
435
Minetto R., J. Leite N. and Stolfi J. (2007).
RELIABLE DETECTION OF CAMERA MOTION BASED ON WEIGHTED OPTICAL FLOW FITTING.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 435-440
Copyright
c
 SciTePress

tails. Section 5 discusses the method used for the opti-
cal flow computing, and Section 6 shows some results
obtained with real videos. In section 7 we present
some conclusions and directions for future works.
2 RELATED WORK
Most existing techniques to determining camera mo-
tion can be classified according to the way they ob-
tain the raw motion data, e.g., from MPEG motion
vectors, by analysis of spatio-temporal textures, or by
analysis of the optical flow.
2.1 Analysis of MPEG Motion Vectors
Some algorithms try to derive the camera motion pa-
rameters directly from the MPEG compressed video
stream (Ewerth et al., 2004). They consider the fact
that the MPEG encoding divides the frame into an ar-
ray of fixed-size blocks, and try to estimate an average
velocity vector within each block. These vectors are
then compared with the velocities that are predicted
from the camera motion parameters. This approach
can be very efficient because it works directly on the
MPEG stream without decompression, and does not
have to compute the motion vectors. However, the
MPEG velocity vectors are chosen on a local basis for
efficient compression, and may diverge considerably
from the actual image motion (Huhn, 2000).
Figure 1: Optical flow between a pair of consecutive video
frames sampled at a regular grid. The area of each dot is
proportional to the weight w
i
of the vector. The camera is
doing a combination of pan to the left and tilt up.
2.2 Analysis of 2D Spatio-Temporal
Slices
A video recording can be seen as a 3D image, with
two space axis x,y and a time axis t. A spatio-
temporal slice is a 2D image of a video, with t as
one axis and an arbitrary line on the x, y plane as the
other axis. Ngo et al (Ngo et al., 2003) proposed an
method to detect camera movement by analysis of 2D
spatio-temporal slices — such as horizontal (x,t) and
and vertical (y,t). The key idea is that camera mo-
tions tend to produce characteristic textures in such
slices. Standard image analysis techniques, such as
histograms of the structural tensor, can then be used
to identify such textures and estimate the motion pa-
rameters from their orientation. The main problem
with this approach is distinguishing camera move-
ment from object motion. Moreover, combinations
of pan/tilt/zoom often causes misclassification.
2.3 Methods Based on Optical Flow
The most reliable methods proposed so far are based
on explicit computation of the optical flow be-
tween consecutive frames. A well-known contribu-
tion by Srinivasan et al. (Srinivasan et al., 1997)
uses the Nelder-Meade non-linear minimization pro-
cedure (Press et al., 1986) to compute the best-fitting
camera-motion parameters. They use a detailed cam-
era motion model, which includes rolling and track-
ing, and also accurately models the pincushion-like
distortion on the flow that is observed when panning
or tilting with a wide angle of view. On the other
hand, their algorithm allows only limited amounts of
scene motion. Moreover, the Nelder-Meade optimiza-
tion algorithm is known to be expensive, and gets eas-
ily trapped in local minima.
3 METODOLOGY
3.1 Weighted Optical Flow
Conceptually, the optical flow from an image I to a
later image J is a function f that, to each point u of the
image domain D, associates a velocity vector f(u),
such that
I(u) ≈ J(u+ f(u)) (1)
whenever u and u + f(u) lie both within D. The
similarity criterion ≈ in equation (1) depends on the
context, but usually includes similarity of image val-
ues and possibly of other local information, such as
derivatives or texture.
Our algorithm assumes that the optical flow f is
sampled at a fixed set of points u
1
,u
2
,.. .,u
n
, yield-
ing a list of vectors f
1
, f
2
,.. ., f
n
. See figure 1.The
algorithm also requires, for each vector f
i
, a corre-
sponding weight w
i
, which expresses its reliability.
The weight is usually higher for points u
i
where the
local texture of image I is easier to track, and was lo-
cated in image J with high confidence.

3.2 The Canonical Motions
The central step in our algorithm is the approxima-
tion of the optical flow field by a combination of three
canonical camera motion flows p, t and z. These
fields are the distinctive optical flows that ideally
would result from a static scene being images which
represent pan, tilt, or zoom motion, with a specific
speed.
The canonical pan flow p, by definition, has
p(u) = (1, 0) at every point u of the image’s do-
main. Similarly, the canonical tilt flow t and zoom
flow z are defined, respectivelly, as t(u) = (0,1) and
z(u) = 2u for all u (see figure 2). We use an im-
age coordinate system whose origin is at the center
of each frame, with the x axis pointing left and y
pointing up. The unit of measurement is such that the
image domain D is the rectangle [−0.500, +0.500] ×
[−0.375,+0.375].
Figure 2: The canonical camera motion flows: pan p(u), tilt
t(u), zoom z(u), sampled at a 7×5 grid of points.
The canonical pan flow corresponds to a rotation
of the camera around the local vertical axis that causes
the aim point to sweep horizontally from right to left,
just fast enough to completely replace the field of
view from one frame to the other. Assuming an an-
gular field of view fairly small.
3.3 Analyzing the Optical Flow
The next step in our algorithm is to approximate the
optical flow f between the two given frames by a lin-
ear combination
˜
f of the canonical flows, namely
˜
f(u) = P∗p(u) + T ∗t(u) + Z ∗z(u) (2)
for every u ∈ D.
The coefficients P, T and Z, to be determined, will
indicate the amount of pan, tilt and zoom, respec-
tively, that seem to have occurred between two con-
secutive frames. Note that a negative value for a coef-
ficient means that the apparent motion is opposite to
the corresponding canonical movement (that is, a pan
to the right, a tilt-up, or a zoom-out, respectively).
We compute the coefficients P, T,Z by a straight-
forward weighted least squares procedure. For that
purpose, we define the scalar product of two flows a
and b, with a weight function w, as
h
a|b
i
=
D
w(u)a(u)b(u)du
D
w(u)
(3)
The discrete version of this formula, assuming that
the images are sampled at points u
1
,u
2
,.. .,u
n
is
hh
a|b
ii
=
∑
n
i=1
w
i
a
i
b
i
∑
n
i=1
w
i
(4)
As usual, we also define the norm of a (sampled) flow
f as
k
f
k
=
p
hh
f|f
ii
. Formulas (3) and (4) obviously
satisfy the definitions of scalar product and norm, as
long as the weights w
i
are all positive.
We seek P, T and Z that minimize the discrep-
ancy between the given flow f and the ideal flow
˜
f of
equation ( 2). The discrepancy is the flow d = f −
˜
f,
and its overall magnitude can be measured by the
square error Q(P, T, Z) =
k
d
k
2
=

f −
˜
f|f −
˜
f

. As
in standard least-squares fitting, the values of P,T,Z
that minimize Q are found by solving the system of
linear equations


hh
p|p
ii hh
p|t
ii hh
p|z
ii
hh
t|p
ii hh
t|t
ii hh
t|z
ii
hh
z|p
ii hh
z|t
ii hh
z|z
ii




P
T
Z


=


hh
f|p
ii
hh
f|t
ii
hh
f|z
ii


(5)
3.4 Weight Adjustment for Vectors
The least-squares method (5) works fine if the scene
is stationary. Moving objects change the optical flow,
and therefore introduce errors in the fitted parame-
ters P, T, and Z, as the least-squares procedure yields
some average of the two flows. This is not a signifi-
cant problem if the moving objects cover a small frac-
tion of the image and/or their speed is small compared
to the camera motion flow. However, if the scene con-
tains fast moving objects, their flow may easily dom-
inate the fitted flow
˜
f.
In order to alleviate this problem, we define the
weights w
i
as being the reliability weights ω
i
pro-
vided by the optical tracking procedure, divided by
the length of the corresponding flow vectors f
i
, that is
w
i
=
ω
i
p
|f
i
|
2
+ ε
2
(6)
where ε is a small constant bias, introduced to avoid
division by zero or very small numbers.
Note that this formula increases the relative
weight of small flow vectors, while reducing that of
large vectors. The justification for this correction is
that small flow vectors are indeed more significant,
statistically, than large ones. If the sampled optical
flow f contains a significant number of very small
vectors mixed with some large ones, the explanation
is that the camera is stationary, and the set K of points
with small vectors is part of the background.

4 ITERATIVE WEIGHT
ADJUSTMENT
The least-squares method implicitly assumes that the
deviations between the observed flow f and the ideal
flow
˜
f are due to independent additive noise with
Gaussian distribution. With this assumption, the least
squares method can be derived from the maximum
likelihood principle.
This assumption may be adequate for static scenes
with rich texture, where the main sources of errors in
the flow f are expected to be due to camera and video
encoding noise. For scenes with moving objects, this
assumption is grossly incorrect: it often happens that
all the flow vectors in a large region of the domain
are completely replaced by large “noise” vectors, all
pointing in the same general direction. In such cases,
the least squares method will produce an average of
the camera and scene motion flows.
To solve this problem, we perform several itera-
tions of the least squares fitting procedure, while ad-
justing the weights so as to exclude from considera-
tion those data vectors that seem to be due to moving
objects.
More precisely, we first compute the mean dis-
crepancy vector µ between the given flow f and the
previously fitted camera motion flow
˜
f:
µ =
∑
n
i=1
w
i
( f
i
−
˜
f
i
)
∑
n
i=1
w
i
(7)
and its standard deviation
σ =


f
i
−
˜
f
i
−µ


2
(8)
Points p whose discrepancy f(p) −
˜
f(p) has length
greater than 3σ are eliminated by setting their weights
to zero. The fitting procedure is then applied again
with the adjusted weights to compute P,T and Z. This
process is repeated until there are no points with dis-
crepancy greater than 3σ.
5 COMPUTING THE OPTICAL
FLOW
To compute the optical flow vectors f
i
, we use the
Kanade-Lucas-Tomasi (KLT) algorithm, modified to
yield also the corresponding reliability weights ω
i
.
The core of the KLT algorithm is a procedure that,
given two images I, J and a point u in the image’s do-
main D, locates a point v = u+ f such that the neigh-
borhood of u in I is most similar to that of v in J. We
use the multi-scale algorithm that computes a first es-
timate of v using low-resolution versions of I and J,
and then improves that estimate by several stages of
local search, increasing the image resolution at each
step. This approach makes the algorithm more robust,
and reduces the overall search time.
At each stage, the displacement vector f is ob-
tained by minimization of the sum of square differ-
ences S(u,v) of the I and J pixel values, within two
comparison windows centered at points u and v, re-
spectively. The radius r of the windows is a parameter
of the algorithm.
As it is described in the literature, the KLT algo-
rithm provides this estimate only indirectly. The stan-
dard implementation performs the multiscale search
in parallel for a list u
1
,u
2
,.. .,u
m
of sample points,
but returns displacement vectors only for those points
with reliable matches. Internally, the algorithm first
evaluates the “matchability” of each sample point u
by computing the matrix
G(u) =
"
∑
(
∂I
∂x
)
2
∑
(
∂I
∂x
)(
∂I
∂y
)
∑
(
∂I
∂x
)(
∂I
∂y
)
∑
(
∂I
∂y
)
2
#
(9)
The summations range over all pixels within the com-
parison window centered at the pixel u. The “matcha-
bility” score λ(u) of u is taken to be the smallest sin-
gular value of the matrix G(u) (Press et al., 1986). It
is claimed that λ is small if pixel values are roughly
constant inside the window, and large for windows
that contain distinctive features such as noise, dots,
corners, strong textures, etc..
The KLT implementation discards any sample
point u
i
whose matchability λ(u
i
) lies below an arbi-
trary threshold. The remaining points are then given
to the multiscale matching procedure, which com-
putes the best displacement vector for each point. The
algorithm then computes the average absolute pixel
difference A(u
i
,v
i
) between the two windows, dis-
cards any point for which this quantity is above a sec-
ond threshold, and returns the surviving pairs (u
i
, f
i
).
We modified the KLT implementation so that it re-
turns the best displacement f
i
and the reliability score
ω
i
of every input point u
i
. We defined the score ω as
the ratio λ(u
i
)/A(u
i
,v
i
) so that a point u
i
gets a low
weight ω if its neighborhood in I is featureless (hence
poorly trackable), or if the algorithm fails to find a
good match in the J image.
This change makes better use of the information
provided by the KLT in the sense that, in any statis-
tical estimation, it is better to use all data, weighted
according to its reliability, than to discard some data
and treat the rest as having the same importance.

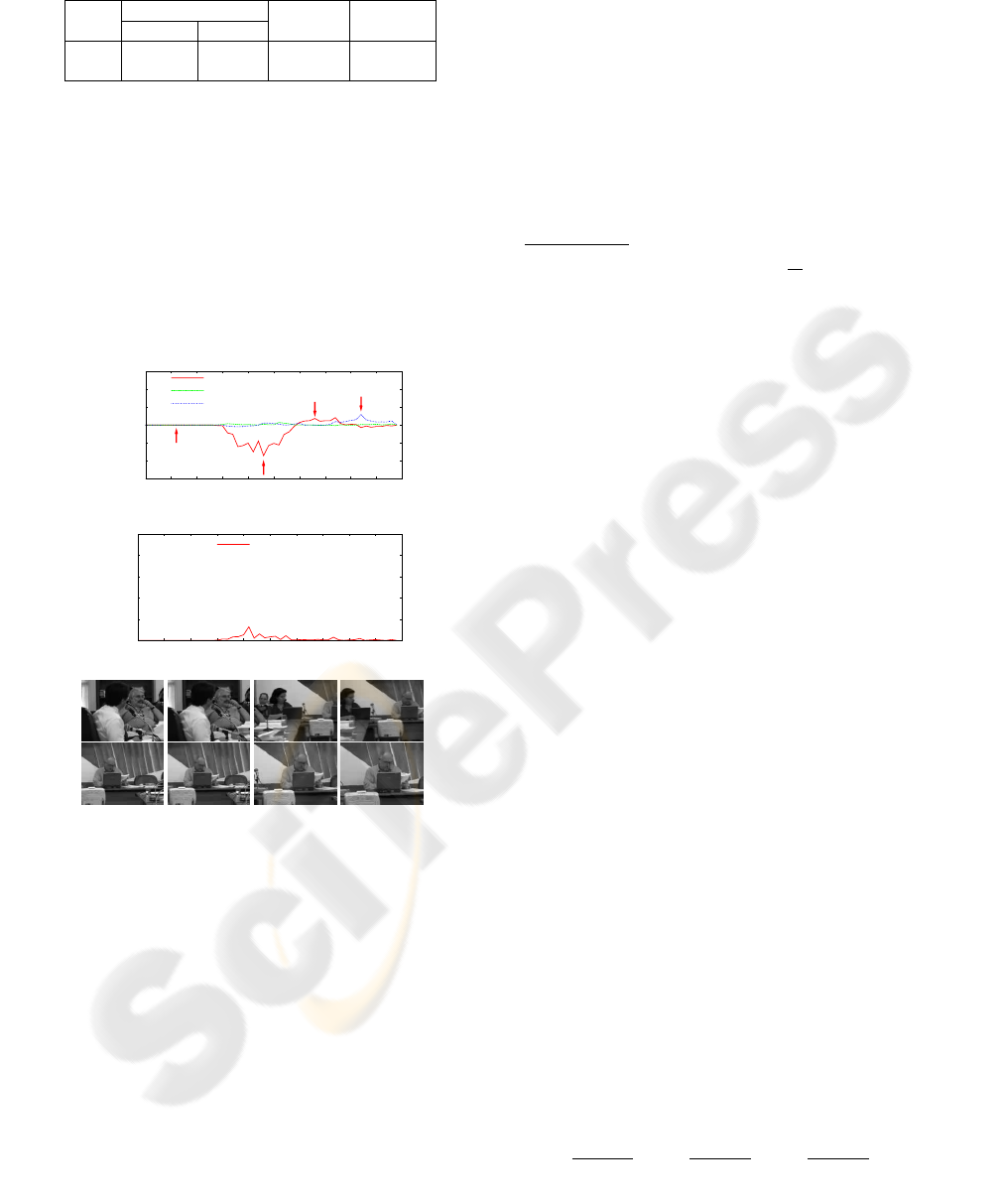
Table 1: Data for the videos used in our experiments.
Video Length Scene M-type
(minutes) (frames) transitions frame pairs
1 39:25 59140 80 1360
2 11:04 16600 23 688
6 TESTS
We tested our algorithm with two continuous video
recordings of our University Council meetings. See
table 1. Both videos were recorded in color, with a
single camera at 320×240 resolution and converted
to grayscale images (PGM) at half the original reso-
lution (to reduce the camera noise, recoding artifacts,
computational costs, etc).
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0 5 10 15 20 25 30 35 40 45 50
motion magnitude
number of frames
L1
L2
L3
L4
P
T
Z
0
2
4
6
8
10
0 5 10 15 20 25 30 35 40 45 50
Q
number of frames
discrepancy
Figure 3: Plots of estimated camera motion coefficients
P, T,Z and residual error Q for 50 consecutive frame pairs
in test video 1. Selected pairs marked L1 through L4 are
shown below. In pair L1 (frames 5 and 6) the camera is sta-
tionary and there is a small amount of scene motion. Frames
14 to 49 comprise a single transition between two speakers.
Pairs L2, L3 and L4 are part of a fast right pan, a slower left
pan, and a zoom-in, respectively.
The comparison window radius r was set to 3 pix-
els (meaning a 7×7 window). We used a regular grid
of 16×11 sample points u
i
, spanning the whole image
minus a safety margin of 34 pixels around the edges.
To evaluate the program’s performance, all con-
secutive frame pairs in the video sequence were clas-
sified by hand into two classes, moving camera (M)
pairs and stationary camera (S) pairs. The scene tran-
sitions in table 1 corresponds to the number of times
one or more camera motion occurred between two pe-
riods of stationary camera.
For every pair of consecutive frames, our program
was used to compute four relevant numbers: the coef-
ficients P, T,Z of the fitted flow, and the magnitude
Q =


f −
˜
f


2
of the discrepancy between the ob-
served and fitted flows. Figure 3 shows the results of
the analysis for 50 consecutive images from video 1,
spanning a scene transition event. Note that the plots
of the P and Z coefficients accurately identify and de-
scribe the transition event.
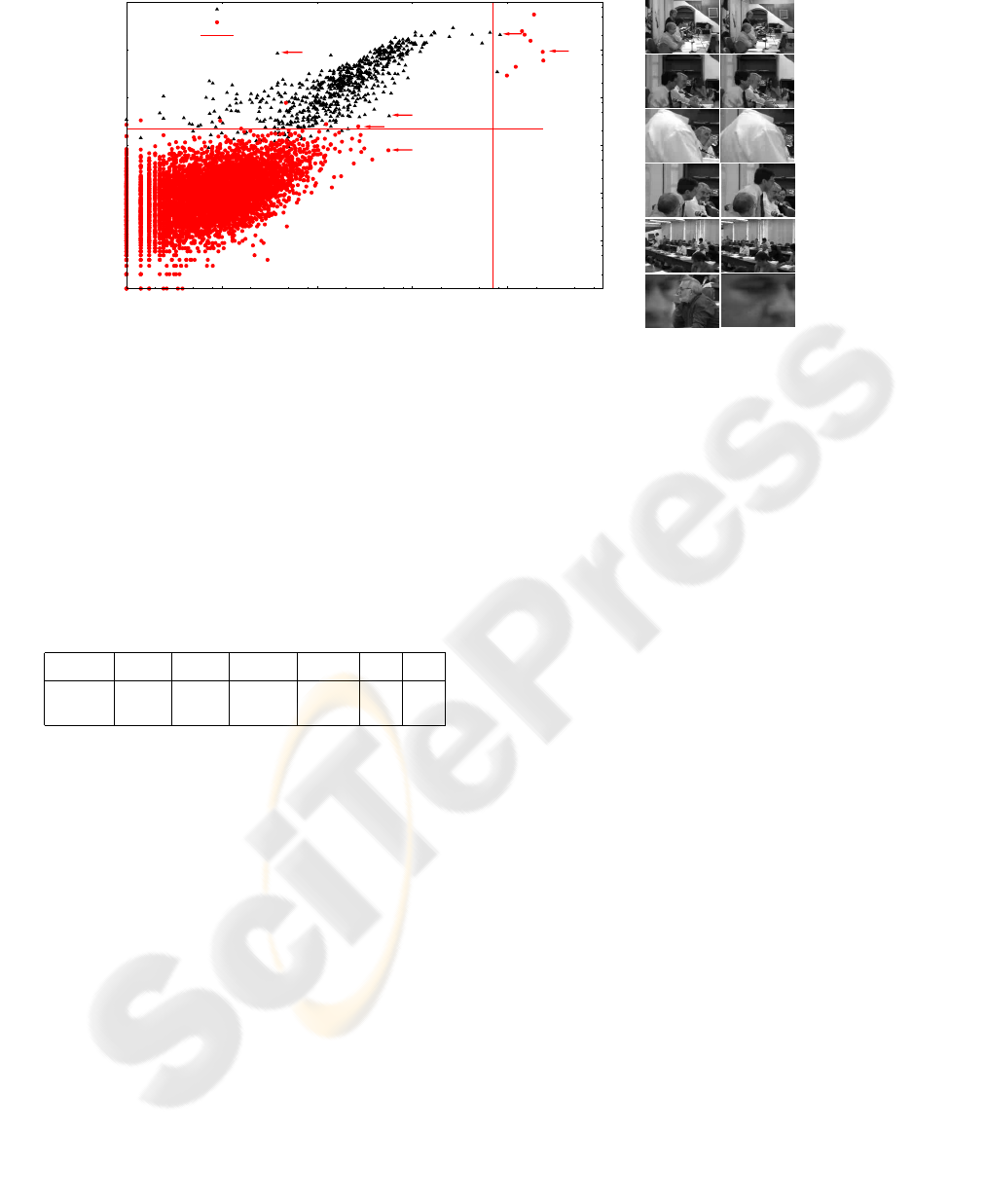
Figure 4 is a log-scale plot of the quantities V =
√
P
2
+ T
2
+ Z
2
(which can be interpreted as the mag-
nitude of fitted flow
˜
f) and E =
√
Q =


f −
˜
f


(the
norm of the residual flow).
Observe that the two classes M and S can be
separated quite cleanly by a simple threshold in V.
Namely, frame pairs with V ≥ 0.0022 are almost al-
ways M, while pairs with V ≤ 0.0022 are almost al-
ways S. The threshold in V corresponds to a fitted
flow where the average vector has length less than one
pixel. The plot shows that the residual errors are very
small, probably due to camera vibration, video noise,
or tracking errors.
The single V threshold fails on a few S frame pairs
with large V, which get classified as M (such as pairs
L3 and L6 in figure 4). Those pairs happen to have
substantial amounts of scene motion, e.g. where most
of the image is blocked by a person walking across
the camera’s field of view. In such cases, the iterative
least-squares procedure ends up rejecting the back-
ground data vectors, and interprets the optical flow
of the moving person as being due to camera motion.
It turns out that many of those false positives also
have a very large residual flow, so they can be dis-
carded by a second threshold in E. Namely, pairs with
V ≥ 0.0022 but E ≥ 7 are more likely to be S frames,
and therefore can be classified as such. An explana-
tion for this fact is that the walking person’s image
is usually out of focus, so the optical flow algorithm
has a hard time finding the correct correspondences.
Moreover, the person is often moving in such a way
that its optical flow cannot be well approximated by a
combination of the basic flows. Both causes typically
lead to large errors. To complete the argument, we
observe that M pairs are rare to begin with, so a frame
pair with large amounts of scene motion is far more
likely to be S than M.
The method’s performance can be quantified by its
precision (p), recall (r) and error (e) metrics, defined
as
p =
T
+
T
+
+ F
+
r =
T
+
T
+
+ F
−
e =
F
+
T
+
+ F
−
(10)
where T
+
is the number of true positives (frame pairs

1e-06
1e-05
1e-04
0.001
0.01
0.1
1
0.001 0.01 0.1 1 10 100
V
E
L6
L5
L1
L2
L3
L4
motion
stationary
threshold
L3
L1
L2
L6
L5
L4
Figure 4: Plot of estimated camera velocity V against residual error E for all frame pairs in test video 2. Frame pairs of type
M (moving camera) and S (stationary camera) are respresented by triangles and circles, respectively. Six events of the video
2 are choosed to show what they represent.
of class M that were correctly identified as such), F
+
is the number of false positives (S pairs identified as
M pairs) and F
−
false negatives (M pairs identified
as S). Table 2 highlights the good performance of the
method through the computation of the above men-
tioned metrics.
Table 2: Precision, recall and error of the algorithm on the
test videos.
Video p r e T
+
F
+
F
−
1 0.98 0.95 0.018 1292 25 68
2 0.99 0.95 0.010 655 7 33
7 CONCLUSION
This paper described a new method for detecting cam-
era motions in video images based on an efficient
weighted least-squares procedure, which defines the
best-fitting between a set of camera motion mod-
els and the computed optical flow of an image se-
quence. This optical flow was obtained through the
KLT tracking method properly modified to give infor-
mation about the camera motion and provide a quanti-
tative analysis of the movements (pan, tilt and zoom)
between two consecutive frames. This modification
yielded also a rough segmentation of the frames into
“foreground” and “background” regions associated,
respectively, with the moving and stationary parts of
a scene.
Tests with real videos of meetings, recorded with
a camera in a fixed location, illustrated the good be-
havior of the method in terms of robustness and ex-
ecution time, as well as its ability to deal with com-
binations of the considered movements. Extensions
to this work include, for instance, analysis of more
elaborated clustering methods to improve the classi-
fication step, filtering the camera parameters to avoid
the influence of brief object motions, and selection of
video key-frames.
REFERENCES
Ewerth, R., Schwalb, M., Tessmanny, P., and Freisleben,
B. (2004). Estimation of arbitrary camera motion in
mpeg videos. 17th International Conference on Pat-
tern Recognition (ICPR), 1:512–515.
Huhn, P. M. (2000). Camera motion estimation using fea-
ture points in mpeg compressed domain. IEEE Inter-
national Conference on Image Processing (ICIP).
Lucas, B. D. and Kanade, T. (1981). An iterative image
registration technique with an application to stereo vi-
sion. In IJCAI81, pages 674–679.
Ngo, C.-W., Pong, T.-C., and Zhang, H.-J. (2003). Motion
analysis and segmentation through spatio-temporal
slices processing. IEEE Transactions on Image Pro-
cessing, 12(3):341–355.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vet-
terling, W. T. (1986). Numerical Recipes: The Art of
Scientific Computing. Cambridge University Press.
Srinivasan, M. V., Venkatesh, S., and Hosie, R. (1997).
Qualitative estimation of camera motion parame-
ters from video sequences. Pattern Recognition,
30(4):593–606.
Tomasi, C. and Kanade, T. (1991). Detection and tracking
of point features. Technical Report CMU-CS-91-132,
Carnegie Mellon University.