LOG-UNBIASED LARGE-DEFORMATION IMAGE REGISTRATION

Igor Yanovsky, Stanley Osher

Department of Mathematics, University of California, Los Angeles

405 Hilgard Avenue, Los Angeles, CA 90095-1555, USA

Paul M. Thompson, Alex D. Leow

Laboratory of Neuro Imaging, UCLA School of Medicine

635 Charles E. Young Drive South, Los Angeles, CA 90095-7332, USA

Keywords:

Nonlinear image registration, information theory, mutual information, log-unbiased deformation, biomedical

imaging.

Abstract:

In the past decade, information theory has been studied extensively in medical imaging. In particular, image

matching by maximizing mutual information has been shown to yield good results in multi-modal image

registration. However, there has been few rigorous studies to date that investigate the statistical aspect of the

resulting deformation ﬁelds. Different regularization techniques have been proposed, sometimes generating

deformations very different from one another. In this paper, we apply information theory to quantifying the

magnitude of deformations. We examine the statistical distributions of Jacobian maps in the logarithmic

space, and develop a new framework for constructing log-unbiased image registration methods. The proposed

framework yields both theoretically and intuitively correct deformation maps, and is compatible with large-

deformation models. In the results section, we tested the proposed method using pairs of synthetic binary

images, two-dimensional serial MRI images, and three-dimensional serial MRI volumes. We compared our

results to those computed using the viscous ﬂuid registration method, and demonstrated that the proposed

method is advantageous when recovering voxel-wise local tissue change.

1 INTRODUCTION

Non-linear image registration is a well-established

ﬁeld in medical imaging with many applications

in functional and anatomic brain mapping, image-

guided surgery, and multimodality image fusion

(Avants and Gee, 2004; Grenander and Miller, 1998;

Thompson and Toga, 2002). The goal of image reg-

istration is to align, or spatially normalize, one im-

age to another. In multi-subject studies, this serves

to reduce subject-speciﬁc anatomic differences by de-

forming individual images onto a population average

brain template.

The deformations that map each anatomy onto a

common standard space can be analyzed voxel-wise

to make inferences about relative volume differences

between the individuals and the template, or statistical

differences in anatomy between populations. Simi-

larly, in longitudinal studies it is possible to visual-

ize structural brain changes that occur over time by

deforming subjects’ baseline scans onto their subse-

quent scans, and using the deformation map to quan-

tify local changes. This general area of computa-

tional anatomy has become known as tensor-based

morphometry (Davatzikos et al., 1996; Shen and Da-

vatzikos, 2003; Thompson et al., 2000).

To construct a deformation that is one-to-one and

differentiable (Christensen et al., 1996; Miller, 2004;

Holm et al., 2004), we must impose a regularizing

constraint. Thus, the problem of image registration is

often cast as a minimization problem with a combined

cost functional consisting of an image matching func-

tional and a regularizing constraint on the deforma-

tion. Common choices of image matching functional

include squared intensity difference, cross correlation

(Collins et al., 1994), and (normalized) mutual in-

formation or other divergence-based or information-

theoretic measures (D’Agostino et al., 2003; He et al.,

2003; Pluim et al., 2004), while choices of regular-

ization usually involve differential operators inspired

by thin-plate spline theory, elasticity theory, ﬂuid

dynamics and the Euler-Poincare equations (Miller,

272

Yanovsky I., Osher S., M. Thompson P. and D. Leow A. (2007).

LOG-UNBIASED LARGE-DEFORMATION IMAGE REGISTRATION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 272-279

 SciTePress

2004; Thompson and Toga, 2000).

2 THEORY

2.1 Global Preservation of Density

Maps

In this paper, we study smooth deformations

h that

map computational domain Ω bijectively onto itself.

Let us assume, without loss of generality, that the vol-

ume of this domain is 1, i.e., |Ω| = 1. The inverse map

h is denoted as

−1

and the Jacobian matrix of

h as

h. The Jacobian map can thus be deﬁned as the de-

terminant of the Jacobian matrix |D

h|.

In volumetric studies, the determinant of the Jaco-

bian matrix (density) applied to any given deforma-

tion

h is an important quantity, encoding the voxel-

wise volume change. As

h (and

−1

) is bijective and

thus globally volume preserving, we have the follow-

ing preservation of global density:

Ω

h(ξ)|dξ =

Ω

d~y = 1,

Ω

−1

(ξ)|dξ =

Ω

d~x = 1.

(1)

Given global preservation of density maps, we can as-

sociate three probability density functions to

−1

and the identity map (id):

(·) = |D

h(·)|,

−1

(·) = |D

−1

(·)|,

(·) = 1.

(2)

Differentiating the identity

−1

(

h(~x)) = ~x on both

sides and setting~y =

h(~x), we obtain

−1

(~y) · D

h(~x) = id, (3)

and hence,

−1

(~y)| · |D

h(~x)| = 1. (4)

By identifying deformations with their corre-

sponding global density maps, we can now apply in-

formation theory to quantifying the magnitude of de-

formations. In our approach, we choose the symmet-

ric Kullback-Leibler (sKL) distance:

sKL(P

) = KL(P

) + KL(P

) (5)

to measure the magnitude of any deformation

h. Here

KL, the Kullback-Leibler distance between two prob-

ability density functions X and Y, is deﬁned as

KL(X,Y) =

Ω

X log

d~x ≥ 0. (6)

To motivate this approach, notice that the ﬁrst part

of sKL measure is simply integrating the log-density

over the entire computational image domain:

Ω

log|D

h(~x)|d~x = −

Ω

log

h(~x)|

d~x

= −

Ω

log

d~x

= −KL(P

) ≤ 0.

(7)

To attach geometric meaning to the second term, we

notice that the KL distance has skew-symmetry with

respect to

h and its inverse

KL(P

−1

) = −

Ω

log|D

−1

(~y)|d~y

Ω



log|D

h(~x)|



h(~x)|d~x

Ω

log

d~x

= KL(P

(8)

where the second equality was obtained using a

change of variables,~y =

h(~x). Similarly, we have

KL(P

) = KL(P

−1

). (9)

2.2 Unbiased Deformation in the

Logarithmic Space

Before developing formulations to construct unbiased

deformations in the logarithmic space, we generalize

equation (7) to the case of mapping regions of interest

(ROI). Assuming we have a priori knowledge that one

ROI is mapped to another, we would like to recover a

mapping that is unbiased in the logarithmic space. In-

tuitively, without further knowledgeother than overall

ROI matching, the resulting Jacobian map should take

a constant value inside the ROI. This can be achieved

using the proposed formulations. Indeed, given any

deformation~g mapping domain A in the source (with

volume a) to domain B in the target (with volume b),

we have the following

log|D~g(~x)|d~x ≤ log

, (10)

with equality obtained if and only if the Jacobian map

of~g takes a constant value (i.e., b/a). This generaliza-

tion can be shown by observing that the logarithmic

mapping is a convex mapping:

∑

log(x

) ≤ nlog(¯x); ¯x =

∑

. (11)

With the above generalization, one can see that, as-

suming the only constraint being an ROI deformation

(a) (b)

Figure 1: Circle-to-Ellipse example. (a) image T; (b) image

S; (c) image T is deformed to image S using Christensen’s

model; (d) image T is deformed to image S using the pro-

posed model. Blue, yellow and red contours represent the

boundaries of objects in T, S, and deformed T, respectively.

Note that for both methods, yellow contour is essentially

invisible due to a very close match. However, the resulting

grid of the proposed method is visually more regular.

(a) (b)

Figure 2: Circle-to-Ellipse example. Jacobian map of the

deformation using (a) Christensen’s model and (b) the pro-

posed model.

from A to B, the unbiased mapping under the logarith-

mic operation has an evenly distributed Jacobian ﬁeld,

which is also intuitively correct (as there is no reason

to assume non-uniformity of the Jacobian ﬁeld).

Given equation (7) and its generalization, we now

propose to quantify the distance between any given

deformation and the identity map by computing the

symmetric KL distance through their density func-

tions. Due to the above mentioned skew-symmetry,

this distance takes the following several equivalent

0 0.2 0.4 0.6 0.8 1 1.2

200

400

600

800

1000

Jacobian

Histogram

Christensen‘s model

0 0.2 0.4 0.6 0.8 1 1.2

200

400

600

800

1000

Jacobian

Histogram

proposed model

Figure 3: Circle-to-Ellipse example. Histograms of Jaco-

bian values of the deformations inside the ellipse for Chris-

tensen’s model and the proposed model.

0 50 100 150 200 250 300 350 400 450 500

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

Iteration number

Standard deviation

Circle−to−Ellipse example: The standard deviation of Jacobian values

Christensen‘s model

proposed model

(a)

0 50 100 150 200 250 300 350 400 450 500

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

Iteration number

Symmetric KL distance

Circle−to−Ellipse example: The symmetric KL distance

Christensen‘s model

proposed model

(b)

Figure 4: Circle-to-Ellipse example. (a) Standard deviation

of Jacobian values inside the ellipse per iteration. (b) Sym-

metric KL distance. For Christensen’s model (dashed blue),

both standard deviation and symmetric KL distance increase

while for the proposed model (solid red), both standard de-

viation and symmetric KL distance stabilize.

forms:

sKL(P

) = sKL(P

−1

)

= KL(P

) + KL(P

−1

)

= KL(P

) + KL(P

)

= KL(P

−1

) + KL(P

)

= KL(P

−1

) + KL(P

−1

)

Ω



h(~x)| − 1



log|D

h(~x)|d~x

Ω



−1

(~y)| − 1



log|D

−1

(~y)|d~y.

(12)

To see why minimizing equation (12) leads to unbi-

ased deformation in the logarithmic space, we ob-

(a) (b)

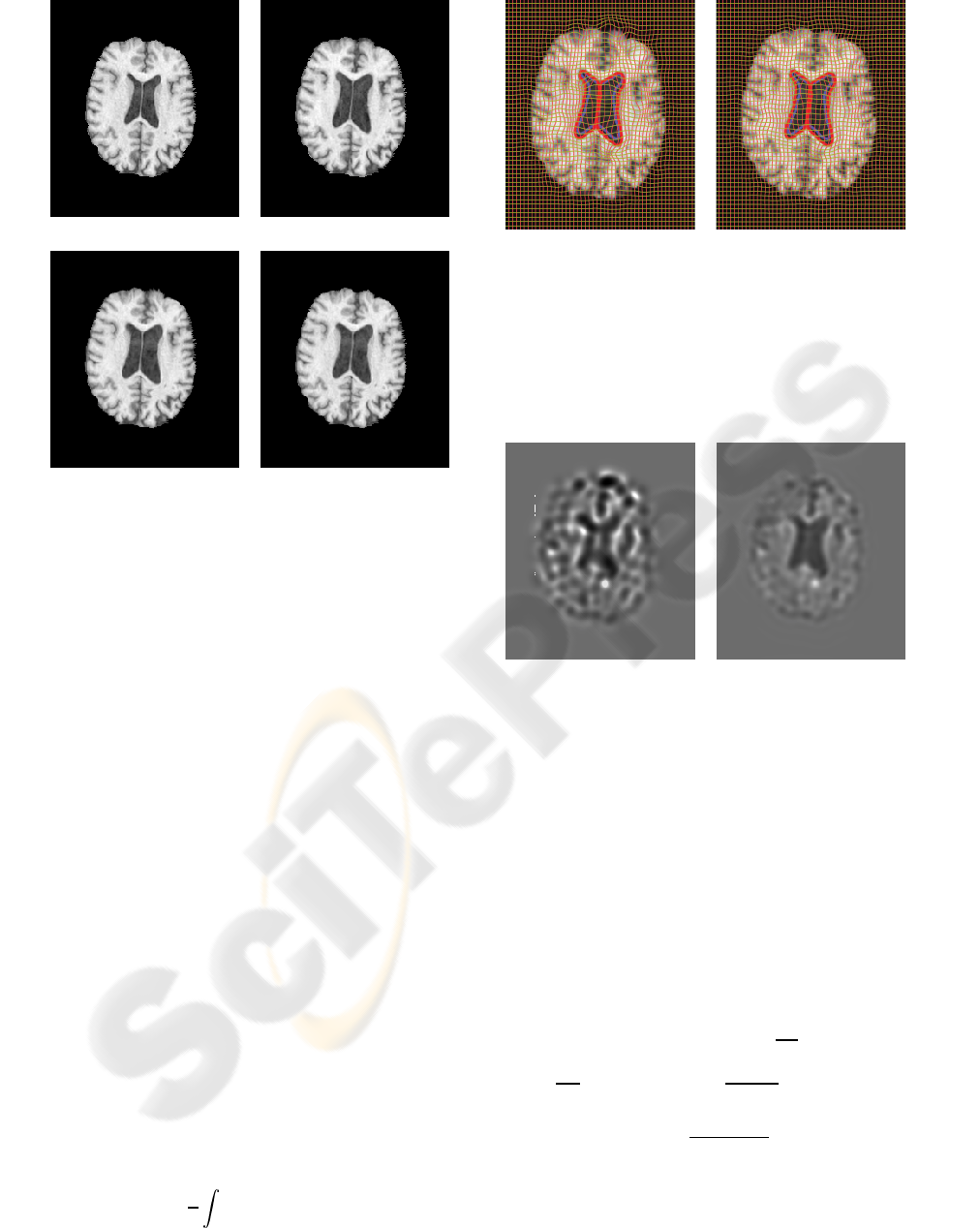
Figure 5: Serial MRI example. (a) image T; (b) image S; (c)

image T is deformed to image S using Christensen’s model;

(d) image T is deformed to image S using the proposed

model.

serve that the integrand is always non-negative, and

only evaluates to zero when

h is volume-preserving

everywhere (Jacobian of

h is 1 everywhere). Thus,

by treating it as a cost, we recover zero-change by

minimizing this cost when we compare images dif-

fering only in noise. Also, this approach is unbiased

for mapping ROIs in the logarithmic space, due to the

inequality in (10).

3 IMPLEMENTATION

Let us denote the template image as T(~x) and the

study image as S(~x) deﬁned on the spatial domain Ω.

We solve for deformation

h, such that T ◦

h matches S,

while minimizing the symmetric KL distance in equa-

tion (12). The deformation

h is usually expressed at

each voxel in terms of the displacement vector~u from

the original position:

h(~x) = ~x −~u(~x). In this paper,

we will use the sum of the squared differences (SSD)

to measure the accuracy of matching between the de-

formed template and the study:

SSD(T,S,~u) =

Ω

|T(~x−~u) − S(~x)|

d~x, (13)

(a) (b)

Figure 6: Serial MRI example. Results obtained with (a)

Christensen’s model and (b) the proposed model. Blue, yel-

low and red contours represent the boundaries of ventricles

in T, S, and deformed T, respectively. Note that for both

methods, yellow contour is essentially invisible due to a

very close match. However, the resulting grid of the pro-

posed method is visually more regular.

(a) (b)

Figure 7: Serial MRI example. Jacobian map of the defor-

mation using (a) Christensen’s model and (b) the proposed

model.

which is also known as a Gaussian sensor model. To

numerically implement our approach, we propose to

minimize a combined cost function

C = SSD+ λ(sKL). (14)

This can be achieved using incremental updating

along the gradient descent of the correspondingEuler-

Lagrange equation. Hence, we obtain the ith compo-

nent of the force ﬁeld:

(~x,~u(~x,t)) = −[T(~x−~u) − S(~x)]

∂T

∂x



~x−~u

−λ

∑

∂

∂x





1+ log|D

h(~x)| −

h(~x)|



(~x)





h(~x)



−1



(~x)



h(~x)|

(15)

where Co

is the matrix cofactor of the (i, j)-th com-

ponent of the Jacobian matrix D

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8

100

200

300

400

500

600

Jacobian

Histogram

Christensen‘s model

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8

100

200

300

400

500

600

Jacobian

Histogram

proposed model

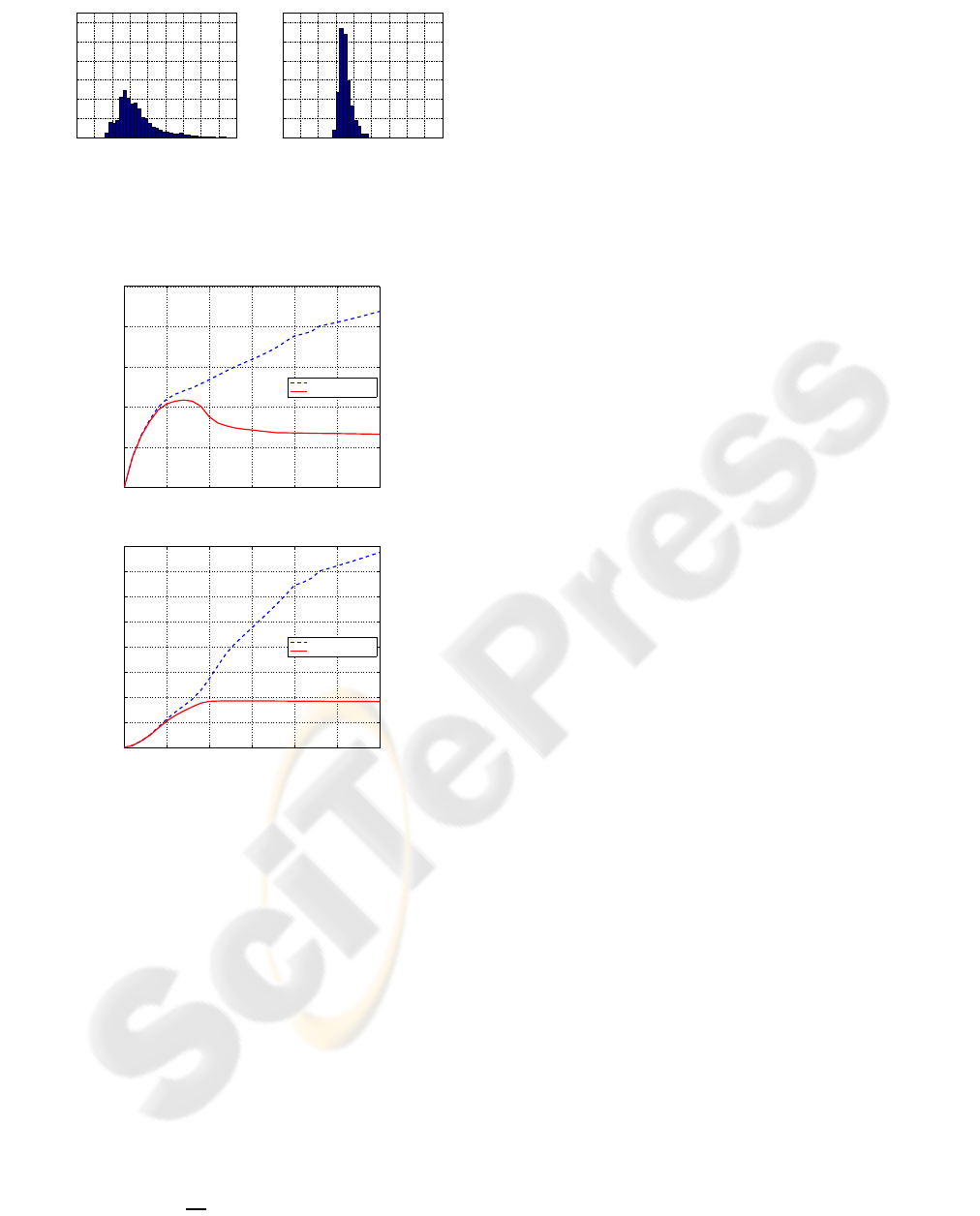
Figure 8: Serial MRI example. Histograms of Jacobian val-

ues of the deformations inside ventricles for Christensen’s

model and the proposed model.

0 50 100 150 200 250 300

0.05

0.1

0.15

0.2

0.25

Iteration number

Standard deviation

MRI example: The standard deviation of Jacobian values

Christensen‘s model

proposed model

(a)

0 50 100 150 200 250 300

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

Iteration number

Symmetric KL distance

MRI example: The symmetric KL distance

Christensen‘s model

proposed model

(b)

Figure 9: Serial MRI example. (a) Standard deviation of

Jacobian values inside the ventricle per iteration. (b) Sym-

metric KL distance. For Christensen’s model (dashed blue),

both standard deviation and symmetric KL distance increase

while for the proposed model (solid red), both standard de-

viation and symmetric KL distance stabilize.

In this paper, we follow the approach in

(D’Agostino et al., 2003) solving the viscous ﬂuid

model (Christensen et al., 1996). Of note, in (Chris-

tensen et al., 1996), the authors used the sum of the

squared differences (SSD) as a cost functional for

minimization (no control over the distribution of the

Jacobian values was employed). Given the velocity

ﬁeld~v, the following partial differential equation can

be solved to obtain the displacement ﬁeld~u:

∂~u

∂t

=~v−~v·

∇~u. (16)

The instantaneous velocity as in (D’Agostino et al.,

2003) is obtained by convolving

f with Gaussian ker-

nel G

of variance σ:

~v = G

∗ (−

f(~x,~u)). (17)

4 RESULTS AND DISCUSSION

In this section, we implemented and tested the pro-

posed nonlinear registration model. The deforma-

tion ﬁelds were computed using adaptive time step-

ping, with maximal change in displacement of 0.1 al-

lowed in each iteration. In order to obtain a fair com-

parison between the proposed and the viscous ﬂuid

method, re-gridding was not employed. Re-gridding

is essentially a memoryless procedure, as how im-

ages are matched after each re-gridding is indepen-

dent of the deformation before the re-gridding, ren-

dering the comparison of ﬁnal Jacobian ﬁelds and cost

functionals problematic. Moreover, the strategy of re-

gridding, through the relaxation of deformation over

time, is less rigorous from a theoretical standpoint.

In order to gain more insight into the effect of the

symmetric KL distance term in (12), we ﬁrst consider

matching two binary synthetic images. In Figures 1

through 4, we show the results of deforming a disk

into an ellipse (both 128 by 128; λ = 500 in (15)).

As seen in Figure 1(c,d), both the ﬂuid registration

(Christensen’s) model and the proposed model gener-

ated a close match between the deformed image and

the study. Here, optimal matching was considered

achieved once the overall cost functional stopped de-

creasing. However, as seen in Figures 2 and 3, the

proposedmethod more evenly distributesdeformation

inside and outside an ellipse (resulting from the con-

vex property of the logarithmic mapping in inequality

(10)). Note the vertical stretching of the grid in the

center of the ellipse for the proposed method, which

is a consequence of uniform distribution of Jacobian

values. On the other hand, using Christensen’s model,

the grid does not uniformly adjust to object’s volume

change; this is especially noticeable in the center of

the ellipse. Figure 4(a) plots the standard deviation

of the Jacobian ﬁeld inside the ellipse as a function

of iteration number. For Christensen’s model, the

standard deviation inside the ellipse increased with

the number of iterations, while the proposed method

yielded an optimized standard deviation as more it-

erations were computed. The proposed symmetric

KL distance also increased for Christensen’s method,

while it was minimized for the proposed method as

shown in Figure 4(b).

In Figures 5 through 9, we show the results of

matching a pair of 2D slices from a set of Serial MRI

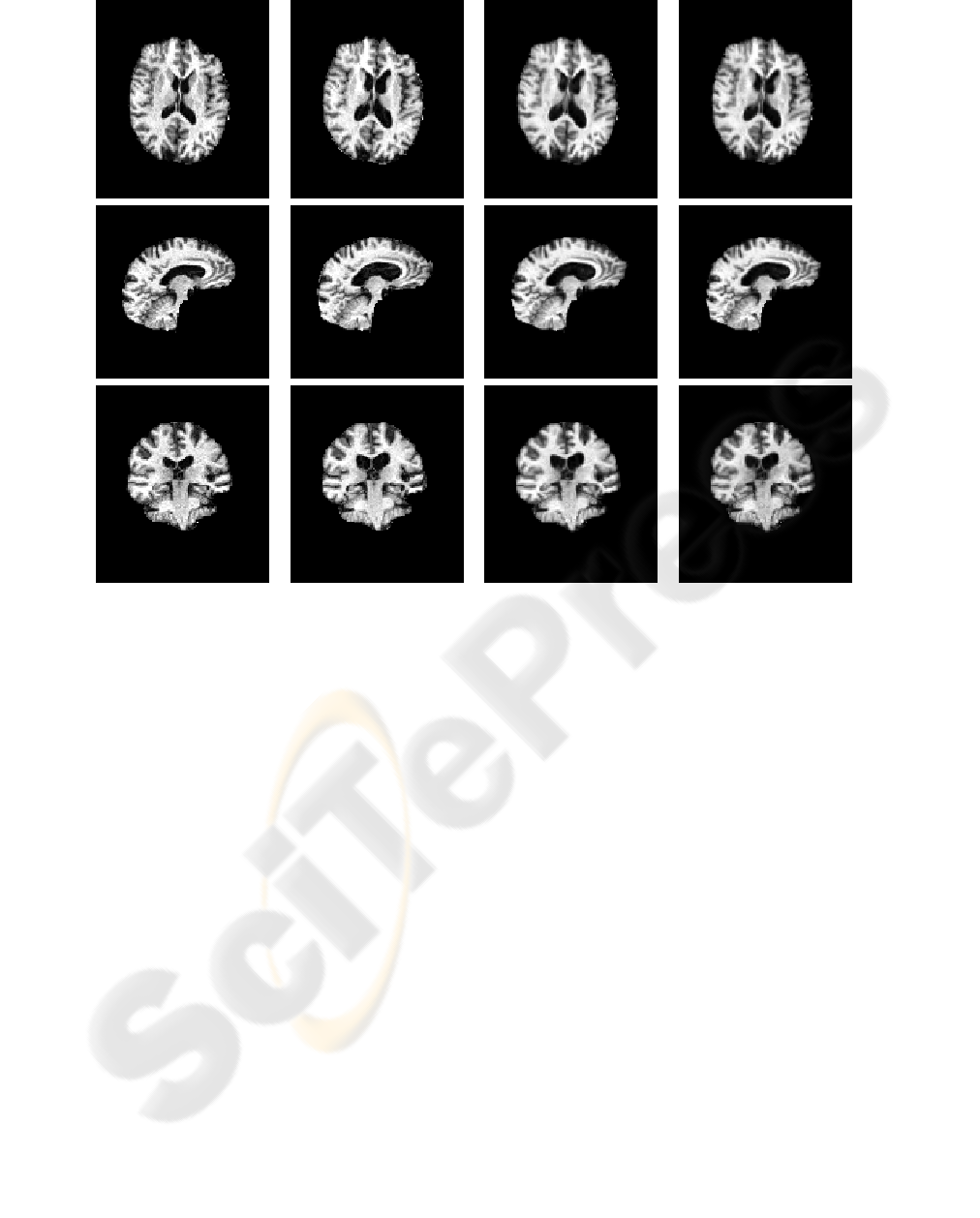
(a) (b) (c) (d)

Figure 10: 3D Serial MRI example. Rows depict slices in axial (row 1), sagittal (row 2), and coronal (row 3) planes. Columns

depict (a) T; (b) S; (c) T deformed using Christensen’s model; (d) T deformed using the proposed model.

images (each of size 226 by 256; λ = 400 in (15)),

where visually signiﬁcant ventricle enlargement is

present. Both Christensen’s method and the proposed

model generated a close match between the deformed

image and the study (Figure 5(a-d)). Here, there is no

reason to not evenly distribute Jacobian ﬁeld inside

the ventricles, as realized using the proposed method.

In contrast, Christensen’s method generated a density

map with extreme values along the ventricular bound-

ary. Indeed, given the overall longitudinal ventricu-

lar dilatation, we argue that the corresponding density

change map should be constant inside the ventricle.

As seen in Figure 9, both the standard deviation inside

the ventricle and the symmetric KL distance increased

for Christensen’s method, while these quantities sta-

bilized for the proposed method.

In the last numerical example (Figures 10

through 12), we tested the proposed model using

two 3D Serial MRI volumes obtained from a patient

with right-side temporal atrophy (6 years apart; each

of size 112x128x128; λ = 500). In this example,

the same conclusions were reached, demonstrating

both the numerical and theoretical advantages of our

method. In particular, in Figure 11(b), right temporal

atrophy (RT) and ventricular enlargement (V) are eas-

ily visualized in the Jacobian map generated using the

proposed method, while Christensen’s method gener-

ated a very noisy map (Figure 11(a)).

5 FUTURE DIRECTIONS

This paper introduces a new framework for the con-

struction of diffeomorphic maps that yield theoreti-

cally and intuitively correct Jacobian statistics. Simi-

lar concept can be applicable to constructing joint reg-

istration and segmentation algorithms, with the lat-

ter based on Jacobian values. To this end, we are

currently investigating a level set method (Osher and

Sethian, 1988; Osher and Fedkiw, 2003) based imple-

mentation (Chan and Vese, 2001) that would alow us

to simultaneously register serial images and identify

regions of atrophy/expansion.

The idea of employing symmetric KL distance in

nonlinear image registration presented in this work

(a) (b)

Figure 11: 3D Serial MRI example. Jacobian map overlaid

with the deformed volume for Christensen’s model (column

a) and the proposed model (column b), with localized atro-

phy in right temporal area. Rows depict slices in axial (rows

1 and 2), sagittal (row 3), and coronal (row 4) planes.

is also closely related to other scientiﬁc ﬁelds. For

example, optimization problems involving Jacobian

operator are commonly encountered in grid gener-

ation (Liseikin, 1999) and in continuum mechanics

and computational physics, where the Hencky tensor

arises in modeling very large deformations. However,

we believethat the logarithmic transform has not been

0 100 200 300 400 500 600 700

0.05

0.1

0.15

0.2

0.25

Iteration number

Standard deviation

3D MRI example: The standard deviation of Jacobian values

Christensen‘s model

proposed model

(a)

0 100 200 300 400 500 600 700

0.002

0.004

0.006

0.008

0.01

0.012

Iteration number

Symmetric KL distance

3D MRI example: The symmetric KL distance

Christensen‘s model

proposed model

(b)

Figure 12: 3D Serial MRI example. (a) Standard devia-

tion of Jacobian values inside the ventricle per iteration. (b)

Symmetric KL distance.

formally introduced in the grid generation literature

and may also be useful there.

ACKNOWLEDGEMENTS

The authors would like to thank James Becker and

Simon Davis at the University of Pittsburgh for pro-

viding the MRI dataset.

This work was supported by Grants U54

RR021813 NIH/NCRR, Grant U01 AG024904,

and Grants R21 RR019771, EB01651, AG016570,

NS049194 to PT.

REFERENCES

Avants, B. and Gee, J. C. (2004). Geodesic estimation for

large deformation anatomical shape averaging and in-

terpolation. NeuroImage, 23. suppl. 1, S139-50.

Chan, T. F. and Vese, L. A. (2001). Active contours with-

out edges. IEEE Transactions on Image Processing,

10(2):266–277.

Christensen, G., Rabbitt, R., and Miller, M. (1996). De-

formable templates using large deformation kine-

matics. IEEE Transactions on Image Processing,

5(10):1435–1447.

Collins, D. L., Peters, T. M., and Evans, A. C. (1994). Auto-

mated 3d nonlinear deformation procedure for deter-

mination of gross morphometric variability in human

brain. In Proceedings of The International Society for

Optical Engineering (SPIE) 2359, pages 180–190.

D’Agostino, E., Maes, F., Vandermeulen, D., and Suetens,

P. (2003). A viscous ﬂuid model for multimodal

non-rigid image registration using mutual informa-

tion. Medical Image Analysis, 7:565–575.

Davatzikos, C., Vaillant, M., Resnick, S. M., Prince, J. L.,

Letovsky, S., and Bryan, R. N. (1996). A computer-

ized approach for morphological analysis of the cor-

pus callosum. J. Comput. Assist. Tomogr., 20(1):88–

97.

Grenander, U. and Miller, M. I. (1998). Computational

anatomy: An emerging discipline. Quarterly of Ap-

plied Mathematics, 56:617–694.

He, Y., Hamza, A. B., and Krim, H. (2003). A general-

ized divergence measure for robust image registration.

IEEE Trans. Signal Process, 51(5). 1211-20.

Holm, D. D., Ratnanather, J. T., Trouve, A., and Younes, L.

(2004). Soliton dynamics in computational anatomy.

NeuroImage, 21. suppl. 1, S170-S178.

Liseikin, V. (1999). Grid Generation Methods. Springer-

Verlag, Heidelberg.

Miller, M. I. (2004). Computational anatomy: shape,

growth, and atrophy comparison via diffeomorphisms.

NeuroImage, 23. suppl. 1, S19-S33.

Osher, S. and Fedkiw, R.(2003). Level Set Methods and Dy-

namic Implicit Surfaces. Applied Mathematical Sci-

ences. Springer-Verlag, New York.

Osher, S. and Sethian, J. (1988). Fronts propagating

with curvature dependent speed; algorithms based

on Hamilton-Jacobi formulations. J. Comput. Phys.,

79:12–49.

Pluim, J. P. W., Maintz, J. B. A., and Viergever, M. A.

(2004). f-information measures in medical image reg-

istration. IEEE Transactions on Medical Imaging,

23(12). 1508-1516.

Shen, D. and Davatzikos, C. (2003). Very high-

resolution morphometry using mass-preserving defor-

mations and hammer elastic registration. NeuroImage,

18(1):28–41.

Thompson, P. M., Giedd, J. N., Woods, R. P., MacDon-

ald, D., Evans, A. C., and Toga, A. W. (2000).

Growth patterns in the developing brain detected by

using continuum mechanical tensor maps. Nature,

404(6774):190–3.

Thompson, P. M. and Toga, A. W. (2000). Elastic image

registration and pathology detection. In Bankman, I.,

editor, Handbook of Medical Image Processing. Aca-

demic Press.

Thompson, P. M. and Toga, A. W. (2002). A framework for

computational anatomy. Computing and Visualization

in Science, 5:13–34.