MRI SEGMENTATION USING MULTIFRACTAL ANALYSIS

AND MRF MODELS

Su Ruan

CReSTIC, Dept GEII, IUT de Troyes, 10026 Troyes Cedex, France

Jonathan Bailleul

GREYC, ENSICAEN, 6 Bd. Maréchal Juin, 14050 Caen Cedex, France

Keywords: Multifractal analysis, Markov Random Field, image segmentation, Magnetic Resonance Imaging.

Abstract: In this paper, we demonstrate the interest of the multifractal analysis for removing the ambiguities due to

the intensity overlap, and we propose a brain tissue segmentation method from Magnetic Resonance

Imaging (MRI) images, which is based on Markov Random Field (MRF) models. The brain tissue

segmentation consists in separating the encephalon into the three main brain tissues: grey matter, white

matter and cerebrospinal fluid (CSF). The classical MRF model uses the intensity and the neighbourhood

information, which is not robust enough to solve problems, such as partial volume effects. Therefore, we

propose to use the multifractal analysis, which can provide information on the intensity variations of brain

tissues. This knowledge is modelled and then incorporated into a MRF model. This technique has been

successfully applied to real MRI images. The contribution of the multifractal analysis is proved by

comparison with a classical MRF segmentation using simulated data.

1 INTRODUCTION

Image segmentation is a classical problem in

computer vision and of paramount importance to

medical imaging. Proper tissue classification

enables: a) quantitative volumetric analysis on

various brain structures; b) morphological analysis

to assess intracranial deformation caused by brain

tumours; c) visualisation for surgical planning and

guidance.

In this paper, we deal with tissue segmentation of

Magnetic Resonance Imaging (MRI) brain images.

Numerous semi-automatic and automatic

segmentation techniques have already been

developed to replace manual segmentation which is

a labour-intensive, subjective and thereby non

reproducible procedure. Actually, the main

techniques are based on: texture analysis

(Schad,1993), histogram threshold determination

(Suzuki, 1991), cluster analysis (Simmons, 1994)

and fuzzy cluster analysis (Pham, 1999), a priori

information about anatomy (Joliot, 1993), or MRF

segmentation (Held, 1997)(Choi, 1997). Although

there exists many image classification algorithms,

the methods usually suffer from the fact that in

practice there is a significant overlap in intensity

values between tissue types, owing to magnetic field

inhomogeneity, susceptibility artefacts and partial

volume effects (one pixel mixed of two or more than

two classes). Our idea, about this issue, is to

describe the brain tissue using the relative intensity

variations, rather than using only absolute intensity

values. The multifractal analysis is adopted here to

this objective. It was first introduced in the context

of turbulence, and then studied as a mathematical

tool as well as in many applications such as image

processing (Sarkar,1995) (Levy-Véhel, 1996)

(Grazzini, 2005). Due to the presence of noise in

MRI images, it is important to take into account

contextual information. This can be done a priori

using MRF models which are appropriate to specify

spatial dependencies by a priori label field

distribution (Geman, 1984) (Choi,1997).

In this paper, we demonstrate the interest of the

multifractal analysis to remove the ambiguities due

to the intensity overlap and propose a tissue

segmentation method based on Markov Random

101

Ruan S. and Bailleul J. (2007).

MRI SEGMENTATION USING MULTIFRACTAL ANALYSIS AND MRF MODELS.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications, pages 101-106

DOI: 10.5220/0002046901010106

 SciTePress

Field (MRF) models. The brain segmentation

consists in separating the encephalon into the three

main brain tissues: grey matter, white matter and

CSF. The classical MRF model uses the intensity

and the neighbourhood information, but it is not

robust enough to solve the problems such as partial

volume effects. Therefore, we propose to

supplement the multifractal analysis to the classical

MRF model, which can provide the information

about intensity variations of the brain tissues.

2 MULTIFRACTAL ANALYSIS OF

IMAGES

It is well known that the geometrical complexity of a

“fractal” set may be described, in a global way, by

giving its dimension. In order to describe the local

singular behaviour of measures or signals, the

multifractal analysis is proposed to give either

geometrical or probabilistic information about the

distribution of points having the same singularity

(Levy-Véhel, 1996, 2000). The value of Hölder

exponent α is usually used to obtain a local

information about the pointwise regularity. The so-

called “multifractal spectrum” f(

) gives the

geometrical or probabilistic information. Some

spectra, such as Hausdorff spectrum f

and large

deviation spectrum f

, have been defined and studied

(Levy-Véhel,1998). The multifractal analysis of

images usually consists in computing values of

Hölder exponentα and its multifractal spectrum,

then classifying each point according both to the

value of Hölder exponent α and to the corresponding

spectrum f(

). In this paper, we are only interested

in the local information provided by the Hölder

exponent 

2.1 The Hölder Exponent α

Let μ be a Borel probability measure laid upon a

compact set P. For each point x in P, the Hölder

exponent α can be defined as follows (Levy-Véhel,

1996)(Canus 1996) (more rigorous and complete

definitions are given in (Brown, 1992) (Levy-

Véhel,1998)):

log

))((log

lim)(

→

= (1)

where

)(xB

is an open-ball of diameter

centred

on the point x. It reflects the local behaviour of the

measure

around x. In image analysis, the points in

the equation (1) are naturally associated to the pixels

of the image, the open-balls to windows in 2D and

balls in 3D centred on each pixel, the measures to

functions of grey level intensities. In our case, the

measure

is defined as the sum of the grey level

intensities of pixels within a neighbourhood V

(δ)

defined by a ball of diameters

The Hölder

exponent α can be assessed as the slope of

log[

(V(

))] versus log

changes linearly from 1

to the maximum value with unity step. If the

maximum diameter of the neighbourhood is chosen

small, α reacts to localize singularities. If the

maximum diameter is large, α reacts to more

widespread singularities. Thanks to the choice of the

measure function

(V(

)), we can obtain the

following local information via the Hölder exponent:

let us note α0 the Hölder exponent within a intensity

uniform (homogeneous) region. If the value of

for

the current pixel is higher than

0, it is surely within

a intensity concave region (valley), while in the

inverse case, the current voxel is in a intensity

convex region (hill). The illustration of the different

values of α is shown in Figure 1. In fact,

(V(

)) in a

concave region increases more rapidly in function of

) than that in a convex region. The value α0 lies

between them.

Figure 1: Illustration of α for different spatial variations of

intensity.

2.2 MRI Images

The local image information provided by α is very

helpful in the situation of low contrast, since it can

discriminate the three situations described above. As

known, the cortex of the brain has many

circumvolutions. Thus, it leads to intensity

variations in image, which can be easily described

by the multifractal analysis. In MRI images, the

sulcus can be considered as a valley in term of

intensity, and the CSF is generally at the bottom of

the valley. On the contrary, the gyrus can be

considered as a hill, and the white matter,

surrounded by the grey matter, is at the top of the

hill. The problems of the partial volume effects and

of the low contrast are essentially present in these

two types of regions. Most of the homogeneous

regions can be found within the white matter (in the

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

102

center of the brain) and a few others within the grey

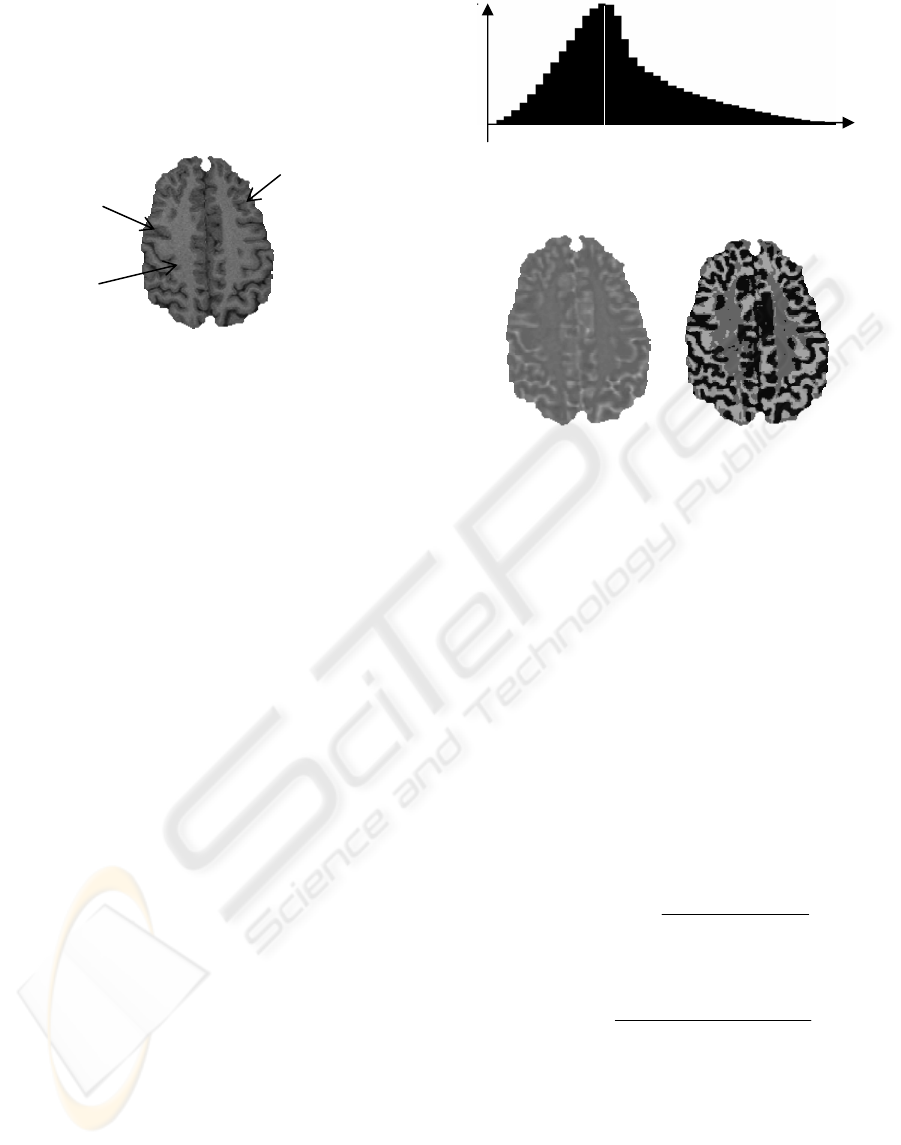
matter. The Figure 2 shows one axial MRI slice in

which examples of the three types of region are

pointed out.

Figure 2: Three regions in MRI data: convex, concave and

homogeneous region

The difficulties of the segmentation are mainly

founded in the regions of the gyri and sulci due to

the partial volume effects. The a priori knowledge

about these two regions described by the Hölder

exponent

can help us to cope with this problem.

The histogram of

obtained from a T1-wheighted

MRI data set (256×256×124 pixels, with a resolution

of 0.9375×0.9375×1.2mm³) is shown in Figure 3. Its

form is always concave for the MRI data, because of

the brain morphology. In fact, the area of the

homogeneous region, usually in white matter, is

larger than that of the others regions (concave and

convex regions). Therefore,

describing an

homogeneous region, can be easily found by

detecting the peak of the histogram. Since we are

just interested in three types of region (concave,

homogeneous and convex), and do not pay attention

to the degree of concavity or convexity, we can

define a function f(

) as follows to obtain the three

types of region :

⎪

⎩

⎪

⎨

⎧

>−

)( 1

)( 0

)( 1

)(

αα

x if

xif

(2)

Figure 4 shows one

slice (the original image is

shown in Figure 2) and the three types of region

obtained using (2) : concave, convex and

homogeneous regions. The measure region is a cube

of 3×3×3 pixels. The value of

0, found from the

peak of the histogram of

is 2.29. Comparing to the

original image, it can be observed that the

homogeneous regions correspond mainly to the

white matter, and the values of

correctly reflect

the hills and valleys in the image.

Figure 3: Histogram of α calculated from a 3D MRI

volume. The measure region is 3x3x3 voxels.

Figure 4: One slice of α image (left) and the three types of

region (right): convex region in deep grey colour, concave

region in white colour and homogeneous in light grey

colour.

3 MARKOVIAN

SEGMENTATION

We propose to incorporate a priori information about

multifractal characterisation into the MRF model.

Let us consider three random fields: Y={Ys, s

∈

represents the field of observations located on a

lattice S of N sites s, X={Xs, s

∈

S} the label field and

A={

s, s

∈

S} the multifractal field. Each Ys takes its

value in

obs

={0…,255}, each Xs in {1=CSF, 2=gray

matter, 3=white matter} and each

s in {-1,0,1

}

(see

equation (2)). We use the Bayes rule to write:

),(

)()/,(

),/(

ssss

sss

xPxyP

yxP

= (3)

Since the two fields Ys and As are independent, (3)

becomes:

),(

)()/()/(

),/(

sssss

sss

xPxPxyP

yxP

= (4)

We look for the x

that maximises the left-hand side

of (4). Since

),(

does not depend on the x

this is equivalent to write:

)()/()/(maxarg

sssss

xPxPxyP

(5)

Sulcus :

Convex region

White matter :

homogeneous

ion

Gyrus:

concave region

MRI SEGMENTATION USING MULTIFRACTAL ANALYSIS AND MRF MODELS

103

In accordance with the Hammersley and Clifford

theorem (Geman, 1984),

)( sxP

is defined by a

Gibbs distribution,

))(exp(

)(

2 ss

xP −≡

(6)

where U2 stands for the energy function and Z is a

normalising constant.

Denoting

))/(exp(

)/( 1 ssss xyU

xyP −= and

))/(exp(

)/(

3 ssss

αα

−= , Eq.(6) can be

defined in terms of an energy function that has to be

minimised:

{}

)7()/()()/(minarg

321 sssss

xUxUxyUx

 Let us consider the terms U1. In MRI data, the

distribution of the grey levels of each tissue has

a gaussian form, and there is no correlation

between them. The data energy term is thus

expressed as :

)2ln(

)(

)/(

xyU

σπ

−

= (8)

 Let’s consider now U

), the energy term

corresponding to the a priori model. We adopt a

3D system of second-order neighbourhood C,

consisting of the 18 nearest neighbours. Using

standard isotropic Potts model, one obtains :

)),(1()(

2 t

Cts

xxxU

∑

∈

−−=

δβ

(9)

where

is a weight coefficient, and is the Kronecker

delta function. U

is minimum for a homogeneous

region.

 The energy term U3

(α

/ x

) is defined in order to

advantage the choice of the CSF label or white

matter label for a site whether it is in a convex

region or a concave region respectively. Since

only two types of region are interesting in our

case, U3

(α

/ x

) can be defined according to

). It becomes :

⎪

⎩

⎪

⎨

⎧

=−

otherwise 0

3 if

1 if

)()/(

3 sconcave

sconvex

sss

xκ

fxU

αα

(10)

where

convexconcave

and are constant (>0).

If one pixel has a grey level near the middle of

the means of the CSF and the gray matter or the

middle of the means of the grey matter and the white

matter, its U

is not dominant. The classification of

this pixel depends mainly on the U

and U

terms.

Therefore, the a priori information brought by U

very useful in this case.

We use the deterministic relaxation algorithm

ICM (Besag, 1974) to minimise the global energy

function U. For the initialisation, we exploit a

maximum likelihood segmentation depending only

on U

4 RESULTS

In order to show the improvement of the

segmentation by addition of the multifractal term

U3, simulated MRI data were used, which are

available on the site BrainWeb (Collins,1998). This

three-dimensional phantom is made up of ten

volumetric data sets that define the spatial

distribution of different tissues (e.g. grey matter,

white matter, CSF, etc), where the voxel intensity is

proportional to the fraction of tissue within the

voxel. A threshold value equal to 50% can be used

to obtain the voxels belonging to the corresponding

tissue, which is considered as the gold standard.

Each volume data consists of 181×217×181 voxels,

whose size is 1×1×1mm3. The simulated MRI

volume with a noise level of 7% is used for our

study. It was firstly segmented by the software

developed in our laboratory (Moretti, 2000) to

obtain the encephalon in which there are only the

three brain tissues (Figure 5).

The segmentation results are evaluated by

measuring the sum, denoted

total

, of the false

positive ratio

and the false negative ratio

is defined as the number of misclassified voxels

divided by the number of good voxels taken from

the gold standard (N). The false negative ratio

defined as the number of lost good voxels divided by

In order to obtain the initial values of the means

and the variances used in U

) to carry out the

initialisation of the segmentation, we used the

Davidon-Fletcher-Powell method described in

(Press, 1992) to fit the intensity histogram of the

encephalon data set by a sum of three gaussian

functions. Since the phantom is relatively realistic,

studies on the choice of the parameters used in the

models were carried out. The parameters β and κ can

be chosen in the ranges

]5.0 ,1.0[

∈

and ]5.1 ,5.0[∈

which provide acceptable

total

. According to our

experience, the algorithm ICM is not very sensitive

to the value βbut rather to the initialisation of the

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

104

segmentation. To reduce this dependence on the

initialisation, the means and variances are re-

estimated at each iteration. A comparison of the

results obtained by the classical Markovian

segmentation and the proposed segmentation method

is performed and shown in Table 1 (β =0.2, κ

convex

concave

=1.1). We can observe that the total error

total

on each tissue is reduced using the function U

in addition. As discussed above, the a priori

information modelled by U

can ameliorate the

results in the case of low contrast. These cases are

usually apparent in the boundaries of tissues or in

gyri and sulci, which represent a small percentage of

total volume data. That is why the improvement is

about 2%. The errors for the CSF segmentation seem

to be more than those for the others. That is because

the number of CSF voxel is much lower than those

of the other tissues, thus it easily results a high

relative error ratio.

Real MRI data were also used to evaluate

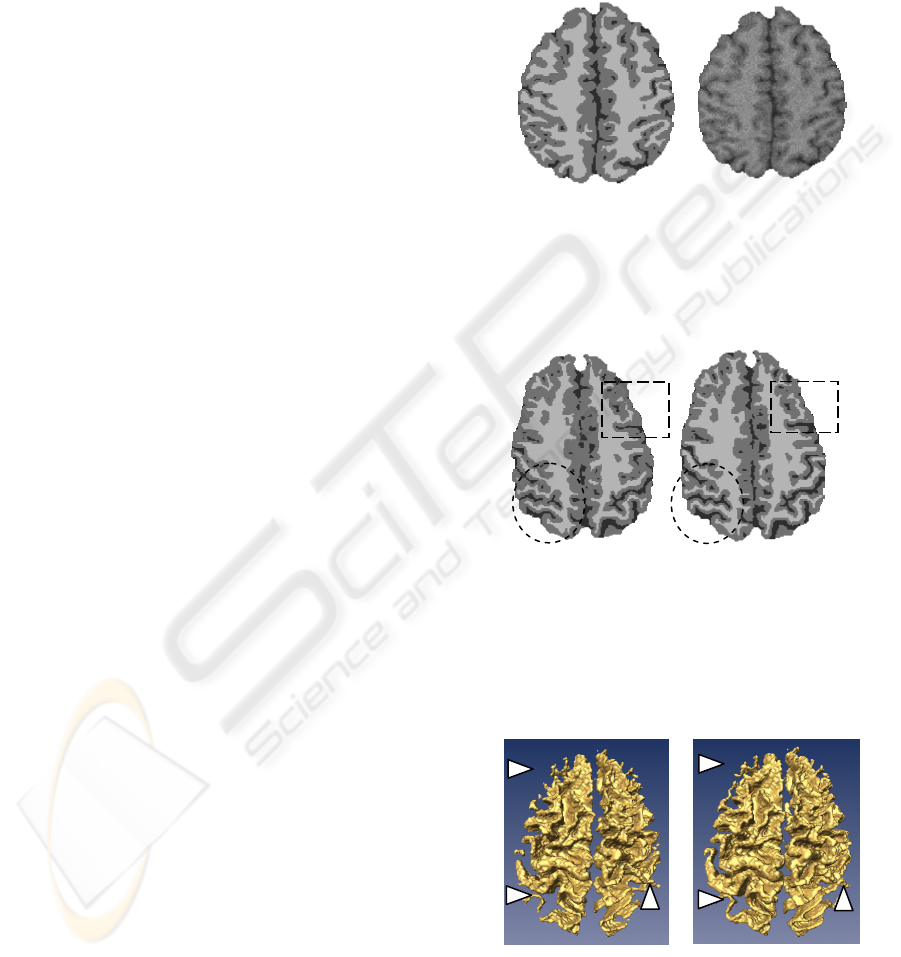
visually the results. The corresponding result of the

image shown in Figure 2 is illustrated in Figure 6.

Compared to the classical Markovian segmentation,

the segmentation integrating the multifractal

information favours the sulci and gyri if the contrast,

due to the partial volume effects, is low in these

regions. Two small windows are located in Figure 6

to show the amelioration in critical regions. The

discontinuities of the white matter and sulci obtained

by the classical MRF segmentation are significantly

repaired by the proposed method. To illustrate more

clearly this issue, volume-rendered images of the

white matter are used (Figure 7). As known, the

white matter of the human is a continuously

connected structure, thus the volume-rendered image

using the proposed method depicts more accurately

the white matter.

5 CONCLUSION

We have presented a MRF segmentation method

incorporating the a priori multifractal information

model, aiming to segment MRI brain tissues. The

Hölder exponent α permits to describe locally the

intensity variations, therefore helping to remove the

ambiguities due to the low contrast and the partial

volume effects. Three types of region: concave,

convex and homogeneous region are used in our

model. The results obtained on the digital phantom

and the real MRI data show quantitatively and

qualitatively improvement of the brain

segmentation.

Although the empirical values, chosen for the

model parameters (

,

convex

and

concave

), give

satisfying results, adapted values to different volume

data will be more efficient and make the

segmentation more accurate. The estimation of these

hyperparameters is an important issue in the future

work.

Figure 5: One slice of gold standard (left) and the

corresponding slice of the simulated data with a level

noise of 7% (right). The three tissues are colour-coded as

follows: white matter =white colour, grey matter =grey

colour, CSF =black.

Figure 6: Comparison of results of the slice shown in

Figure 2 with (right) and without (left) use of the

multifractal analysis. Three tissues are obtained: white

matter (white colour), grey matter (grey colour) and CSF

(black). The improvements can be observed in the circle

windows concerning the white matter and the rectangular

windows concerning the CSF.

Figure 7: Volume-rendered images of the white matter

obtained from the classical MRF segmentation (left) and

the proposed segmentation method (right). Some

discontinuities of structures (left) and improvements

(right) are pointed out by arrows.

MRI SEGMENTATION USING MULTIFRACTAL ANALYSIS AND MRF MODELS

105

Table 1: Comparison of the results obtained by the

classical MRF segmentation (Method 1) and by the

proposed method (Method 2), using the false positive ratio

and the false negative ratio

Method 1 (%) Method 1 (%)

Tissue

total

WM 3.12 8.50 11.62 3.88 5.87 9.7

GM 7.99 5.02 13.01 6.19 5.09 11.2

CSF 13.37 7.78 21.15 10.76 8.78 19.

REFERENCES

Besag, J., 1974. On the statistical analysis of dirty

pictures. J.R. Statist. Soc. B-48, 259-302.

Brown, G., Michon, G. and Peyrière, J., 1992. On the

Multifractal analysis of measures. J.Stat. Phys. 66,

775-790.

Canus, C., Lévy-Véhel, J., 1996. Change detection in

sequences of images by multifractal analysis. Proc. of

ICASSP'96, May 7-10, Atlanta.

Choi, S. M., Lee, J. E. and Kim, M. H., 1997. Volumetric

object reconstruction using the 3D-MRF model-based

segmentation, IEEE. Trans. Med. Imag.16, 887-892.

Collins, D.L. and al., 1998. Design and construction of a

realistic digital brain phantom. IEEE. Trans. Med.

Imag.,17, 463-468 (http: //www.bic.mni.mcgill.ca

/brainweb).

Geman, S. and Geman, D., 1984. Stochastic relaxation,

Gibbs distribution, and the Bayesian restoration of

images. IEEE Trans. Pattern Analysis and Machine

Intelligence 6, 721-741.

Grazzini, J., Turiel, A., Yahia, H., 2005. Presegmentation

of high-resolution satellite images with a multifractal

reconstruction scheme based on an entropy criterium.

Proceeding of IEEE ICIP-2005, Volume: 1, On

page(s): I- 649-52.

Held, K., Kops, E. R., Krause, B. J., Wells, W. M.,

Kikinis, R. and Müller-Gärtner, H. W., 1997. Markov

Random Field segmentation of brain MR images,

IEEE. Trans. on Med. Imag. 16, 878-892.

Joliot, M. and Mazoyer, B., 1993. Three-dimensional

segmentation and interpolation of magnetic resonance

brain images. IEEE Trans. Med. Imag.12, 269-277.

Levy-Véhel, J., 1996. Introduction to the multifractal

analysis of images. In Fractal Encoding and analysis.

Yuval Fisher Editor, Springer Verlag.

Levy-Véhel, J., Vojak, R., 1998. Multifractal analysis of

choquet capacities: preliminary results. Adv.in Appl.

Math. 20, 1-43.

Levy-Véhel, J., 2000. Signal enhancement based on

Hölder regularity analysis. In IMA Volumes in

Mathematics and its Applications, Volume 132, pp.

197-209.

Moretti, B., Fadili, J., Ruan, S., Bloyet, D. and Mazoyer,

B., 2000. Phantom-based performance evaluation-

application to brain segmentation from magnetic

resonance images. Medical Image Analysis, Vol. 4,

No. 4, pp. 303-316, June, 2000.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

106