FACE ALIGNMENT USING ACTIVE APPEARANCE MODEL

OPTIMIZED BY SIMPLEX

Y. Aidarous, S. Le Gallou, A. Sattar and R. Seguier

SUPELEC/IETR, Team SCEE, Avenue de la Boulaie BP 81127, 35511 Cesson Sevigne Cedex, France

Keywords:

Face alignment, Active Appearence Model, Nelder Mead Simplex.

Abstract:

The active appearance models (AAM) are robust in face alignment. We use this method to analyze gesture

and motions of faces in Human Machine Interfaces (HMI) for embedded systems (mobile phone, game con-

sole, PDA: Personal Digital Assistant). However these models are not only high memory consumer but also

efﬁcient especially when the aligning objects in the learning data base, which generate model, are imperfectly

represented. We propose a new optimization method based on Nelder Mead Simplex (NELDER and MEAD,

1965). The Simplex reduces 73% of memory requirement and improves the efﬁciency of AAM at the same

time. The test carried out on unknown faces (from BioID data base (BioID, )) shows that our proposition

provides accurate alignment whereas the classical AAM is unable to align the object.

1 INTRODUCTION

In Human machine interface (HMI) it is necessary

to recognize objects (faces, hands, mouths) and an-

alyze them to identify motions and gestures. All of

these applications ﬁrst need to align objects to be

recognized. We use Active Appearance Models to

align faces on embedded HMI (video phone, game

console). AAM was proposed by Edward, Cootes

and Taylor (G. J. Edwards, 1998) in 1998. They al-

low synthesizing an object with its shape and its tex-

ture. The AAM optimization proposed by Cootes in

(G. J. Edwards, 1998) was based on regression ma-

trix (RM). RM is capable of modifying parameters

to adjust model on an object. Taken of the avail-

able memory in on mobile technology the RM oc-

cupies a signiﬁcant memory space, in order of many

Mega bits. We are going to use Nelder and Mead sim-

plex (NELDER and MEAD, 1965) so as to optimize

model parameters to reconstruct the face. The Nelder

and Mead simplex was used in face feature detec-

tion (Cristinacee and Cootes, 2004). Model of each

landmark (17 landmarks for face) is created and the

simplex optimize the placement of landmarks by us-

ing score function given by each model. The features

models are in low dimension compared by model of

whole face. (Cristinacee and Cootes, 2004) don’t op-

timize AAM parameters but placement of landmarks.

The simplex does not use prior knowledge, which

makes them efﬁcient in generalization and they don’t

need too much memory space as well. The tests per-

formed, treat face alignment in generalization (learn-

ing data base from M2VTS (PIGEON, 1996), Test

data base from BioID (BioID, )). First we introduce

the classical AAM method and its different variant

proposed by community to ﬁnd a solution reducing

required space memory (Section 2). In addition to that

we’ll present in section 3 the AAM simplex adapta-

tion, whereas generalization results are illustrated in

section 4 comparing to results obtained by classical

AAM. In section 5 we’ll conclude and present our fu-

ture works.

2 AAM: USED METHOD

In this section we’ll present classical AAM (G. J. Ed-

wards, 1998) optimized by RM and the problem come

across by this optimization. Subsequently, we’ll in-

troduce some method proposed by community to re-

duce required memory space for RM.

231

Aidarous Y., Le Gallou S., Sattar A. and Seguier R. (2007).

FACE ALIGNMENT USING ACTIVE APPEARANCE MODEL OPTIMIZED BY SIMPLEX.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 231-236

 SciTePress

2.1 Classical Aam

AAM algorithm is constructed in two phases: The

learning phase in which we establish the model, and

the segmentation phase where we search the mod-

elized object in image.

2.1.1 Learning Phase

The learning phase generate mean model of object

from given data base. The shape of an object can be

represented by vector s and the texture (gray level)

by vector g. We apply one PCA on shape and another

PCA on texture to create the model, given by:

= ¯s+ Φ

∗b

= ¯g+ Φ

∗b

(1)

Where s

and g

are shape and texture, ¯s and ¯g are

mean shape and mean texture. Φ

and Φ

are vectors

representing variations of orthogonal modes of shape

and texture respectively. b

and b

are vectors repre-

senting parameters of shape and texture. By applying

a third PCA on vector b





we obtain:

b = Φ∗c (2)

φ is matrix of d

eigenvectors obtained by PCA. c is

appearance parameters vector. The modiﬁcations of c

parameters changes both shape and texture of object.

2.1.2 Segmentation Phase

The objective of this phase is to minimize error be-

tween segmented image and model by choosing pa-

rameters in order to align the model to this image.

To choose good parameters we need an optimization

method. In the case of classical AAM it has been done

with several experiments (by changing each variable

of parameter c). Each training data base object is an-

notated and represented with speciﬁc value of appear-

ance vector c and pose vector t, with the size d

, de-

ﬁned by:

t =



θ S



(3)

Where t

and t

are x and y axis translation, θ is angle

of orientation and S is Scale. Let N be the number of

images, from the data base, of an object to align. Ob-

jects of training data base can be reconstructed from c

appearance vector which contain variations to add to

the mean model. Consider c

, the value of c, which

represents object in the learning data base image i. By

modifying the parameter c

in accordance with :

c = c

+ δc (4)

we create new shape s

and new texture g

(For

example when we displace the model to the right,

we modify t by δt). The vector of error e

is then

= g

−g

,where k is the number of experiments

and g

is the texture of the data base image i under

the shape s

. Then we create experience matrix with

column representing experiment and row number of

pixels in a model (Eq. 5). A column of matrix G

(Eq. 5) is composed of a vector e

. The linear re-

gression give us one linear relation between the gray

level error and pose parameter and another relation

between grey level error and appearance parameter:

T = R

C = R

(5)

C and T are the matrices where the modiﬁcations δc

and δt added to c

and t

(initial pose vector of object

in image i) at the time of each experiment. This gives

us the linear relation between δc and δt:

δt = R

∗δg

δc = R

∗δg

(6)

and R

are the appearance and pose regression ma-

trices respectively. δg is the gray level error on the set

of pixels constituting the object to align. The matri-

ces R

and R

allow us to predict the modiﬁcations of

c and t by having δg to align object. Regression ma-

trix optimization inducts drawback:

-Required memory : column number of regression

matrix is equal to number of model pixels. Row num-

ber is product of number of experiment q with the

number of parameter to be optimized: 4 for R

(Eq. 3)

and as much as parameter as eigenvector retained in

matrix φ (Eq. 2) for R

. RM size is important while

comparing the available memory in embedded tech-

nology.

The searching algorithm in new image is as follow:

1. Generate texture g

and form s according to c pa-

rameter (initially equal to 0).

2. Calculate g

, the image texture which is in the

form s.

3. Evaluate δg

= g

−g

and E

= |δg

4. Predict the modiﬁcation δc

= R

∗δg

and δt

∗δg

which has to be given to the model.

5. Find the ﬁrst attenuation coefﬁcient k (among



1 0.5 0.25



) generate an error E

< E

with E

= |δg

= |g

−g

| , g

is the texture

create by c

= c−k ∗δc

and g

is the texture of

image being in the form s

(form given by c

6. if error E

is not stable, the difference E

−E

i−1

higher than a threshold ζ deﬁned previously, re-

turn to step 1 and replace c by c

When the convergence is reached, the searching form

and texture face is generated with model given by g

and s represented using c

. The number of iterations

required is function of error E

stabilization.

2.2 Direct Appearance Model

This method (X. Hou and Cheng, 2001) is derived

from the classical AAM by eliminating the joint PCA

on texture (Eq.2) and form. It uses the texture infor-

mation directly for the prediction of the form: the es-

timation of position and appearance. It comes from

the fact that we could extract the form directly from

texture. The form and texture are built by PCA. The

main difference between the DAM and the AAM is

in the third PCA. We collect the difference between

the textures generated by small displacements in each

image of the training data base and by carrying out

a PCA on these differences so as to have a matrix of

projection H

. The difference in texture is projected

on under space such as:

δg

′

= H

∗δg (7)

The dimension of δg

′

present a quarter of the dimen-

sion of δg and the prediction is more stable. The re-

gression in the DAM then requires less memory than

the regression used in the AAM. The procedure of re-

search is the same one as the classical AAM except

for the prediction of the new form and texture. In [5]

it is shown that the size of the matrix of regression is

11, 83 lower than that of AAM.

2.3 Active Wavelet Networks

This method (Hu et al., 2003) uses the wavelets as

alternative to the PCA in order to reduce the dimen-

sion of space. It uses a Gabor Wavelet network (Hu

et al., 2003) to model the variations of the texture of

the training base. The GWN approach represents im-

age with a linear combination of functions of 2D Ga-

bor. The given weights are of the form to preserve the

maximum information contained in image for a ﬁxed

wavelet number. The method of search of faces (or

unspeciﬁed object) is the same one as that of the clas-

sical AAM by disturbing the initial positions and to

put a linear relation (matrices of regressions) between

the displacement of the parameters and pixels error.

The DAM and AWN methods make it possible to

reduce the required memory to store RM. In the fol-

lowing section we propose a method to remove the

space allocated to store these matrices.

3 AAM OPTIMIZATION

We propose to use the Training part (Section 2.1.1),

by optimizing the search (Section 2.1.1) appearance

(Eq.2) and pose (Eq.3) parameters by using Nelder

Mead Simplex (SP)[2]. It is a numerical method of

optimization which will allow us to ﬁnd solutions

minimizing pixels error. This method gives us the

possibility of converging in population (together of

solution convergent toward the same minimum) mak-

ing the solution more stable, to be direct: no cal-

culation of derivative and to converge in a number

of iteration which is rather tiny compared to another

global optimization methods requiring a great num-

ber of iteration like the Genetic Algorithms, Simu-

lated Annealing... They will also enable us to reduce

required memory used in classical AAM optimization

by preserving only the average model; we don’t have

to store RM.

3.1 Nelder Mead Simplex Algorithm

The simplex of Nelder Mead (NELDER and MEAD,

1965) makes it possible to ﬁnd the minimum of func-

tion of several variables in an iterative way. For two

variables the simplex is a triangle and the method con-

sists of comparing the values of the function on each

top of the triangle. Thus the top where the function is

highest is rejected to be replaced by another top which

will be calculated according to the precedents. The

algorithm is called simplex considering the general-

ization of the triangle in n dimensions. The stopping

criterion of algorithm will be a threshold of the dif-

ference between the values of the function to be min-

imized given by the current solutions. This threshold

will determine number of iterations necessary to con-

verge. The error to be minimized is the pixels error

[Eq.11] used by the classical AAM.

For new solutions, all the operators of search base

themselves on a center of gravity x

∑

i=1

calcu-

lated compared to the current solutions in each iter-

ation and giving a direction d

= x

−x

n+1

worms

of the solutions minimizing the error function. Let

us note E the objective function to be minimized.

The operators of search for solutions minimizing this

function are as follows:

• The Reﬂection: we test the point which is in the

opposite direction of the bad solution:

= x

n+1

+ 2d

= 2x

−x

n+1

. (8)

• The Expansion: we prolong research beyond the

point of reﬂection by testing the solution:

= x

n+1

+ 3d

= 2x

−x

. (9)

• The Contraction: if the previous two operators of

search fail then we minimize tests points close to

share and other of the current solution:

−

= x

n+1

+ x

)

= x

n+1

+ x

)

(10)

• The Shrinkage: if all the preceding solutions do

not minimize E we narrow down the triangle by

changing these tops, and tests the preceding dis-

turbances.

3.2 Simplex Adaptation to Aam

We propose to adapt the Nelder Mead algorithm

(NELDER and MEAD, 1965) to optimize the AAM

parameters in segmentation phase. The minimized er-

ror is the sum of quadratic errors between real image

and generated model on each pixel:

E =

∑

(11)

A model is described by:

v =





(12)

Size of v is d

+ d

and d

are the c (Eq. 2) and t

size (Eq. 3)), the simplex must optimize d

+ d

pa-

rameters to align the model on the face. The natural

way will be to optimize pose and appearance sepa-

rately like RM (Eq. 6) by implementing two simplex

one for pose and other for appearance. Single simplex

applied on set of parameter will be more efﬁcient (In

quality of time and convergence). The simplex starts

search from d

+ d

+ 1 solutions chosen randomly in

space under constraint. So as to use the simplex al-

gorithm in AAM optimization, stopping criterion and

variables constraint must be deﬁned.

Constraints: they are applied to avoid testing incor-

rect solutions that we know preliminary. These con-

straints bound search space on appearance and pose

variables. We initialize the vector v (Eq. 12), rep-

resenting appearance and pose, randomly in interval

corresponding to each parameter under Cootes’s con-

straint:

• Appearance constraint: appearance variable inter-

val is −2

√

λ et 2

√

λ (Stegmann, 2000). Where λ

is the eigenvalues of the eigenvectors correspond-

ing to matrix G

G, G is the gray level differ-

ence matrix between modifying model and real

image. These constraints are veriﬁed during al-

gorithm execution.

• Pose constraints: AAM is robust till 10% in scale

and translation (T. Cootes, 2002). We initialise

the pose variable (x and y axis translation, rotation

and scale) in the interval of 10% of the object real

pose vector.

Stopping criterion: the algorithm will end after ﬁxed

number of iterations (to insure maximum processing

time) or when it will converge in population. The

population convergence is obtained if difference be-

tween the E values (Eq.11)of the proposed solutions

do not pass the threshold S

. In the case of error

normalization, done by Stegmann in (Stegmann,

2000), the mean value of the error is stable E

mean

on different images of the same object, at the time

when the alignment is correct. We propose to settle

= 0.1×E

mean

Simplexes neither need additional required mem-

ory space necessary to store the model nor informa-

tion on the directions to a priori to minimize the error

E. Typically the number of experiments necessary for

the training phase is 90 (4 for each appearance para-

meter and 6 for each pose parameter). The size of

the two matrices (of appearance R

and of pose R

)

is equal to M ×(d

+ d

) Bytes, M being the num-

ber of pixels contained in texture of the model. For

our test with images 64×64pixels the size of the re-

gression matrices (Eq. 5) is 86KB. The mean model

size is 33KB. The memory require for the AAM is

≈ 120KB. In the case of the simplex we don’t need

RM, therefore the memory used is 33KB. Memory

space required by the simplex is lower than that used

in (Hu et al., 2003) which memorizes the wavelet co-

efﬁcients in addition to the model and also lower than

that needed in (X. Hou and Cheng, 2001).

4 RESULTS

To evaluate the performance of our proposed opti-

mization, we tested alignment of face in generaliza-

tion: the tests were realized on faces which not belong

to the training base. The training data base is made

up of 10 images belonging to the European data base

M2VTS (Multi Modal Checking for Teleservices and

Security applications; Fig.2)(PIGEON, 1996). Our

method was tested on images of the base BioID (bio-

metric Identity; Fig.3)(BioID, ). To qualify the con-

vergence of the AAM we will deﬁne an error of mark-

ing. This error f

(i = 1, 2, 3) was calculated for each

part of the face i = eyes, noise, lips such as:

= p

find

− p

real

avec : p

real

∑

r=1

real

et p

find

∑

r=1

find

(13)

real

are the coordinates of the ground truth of the

points of marking of the i part of the face, p

find

the

coordinates of the points of marking of the part of

the face i found by algorithm and Q

is the number

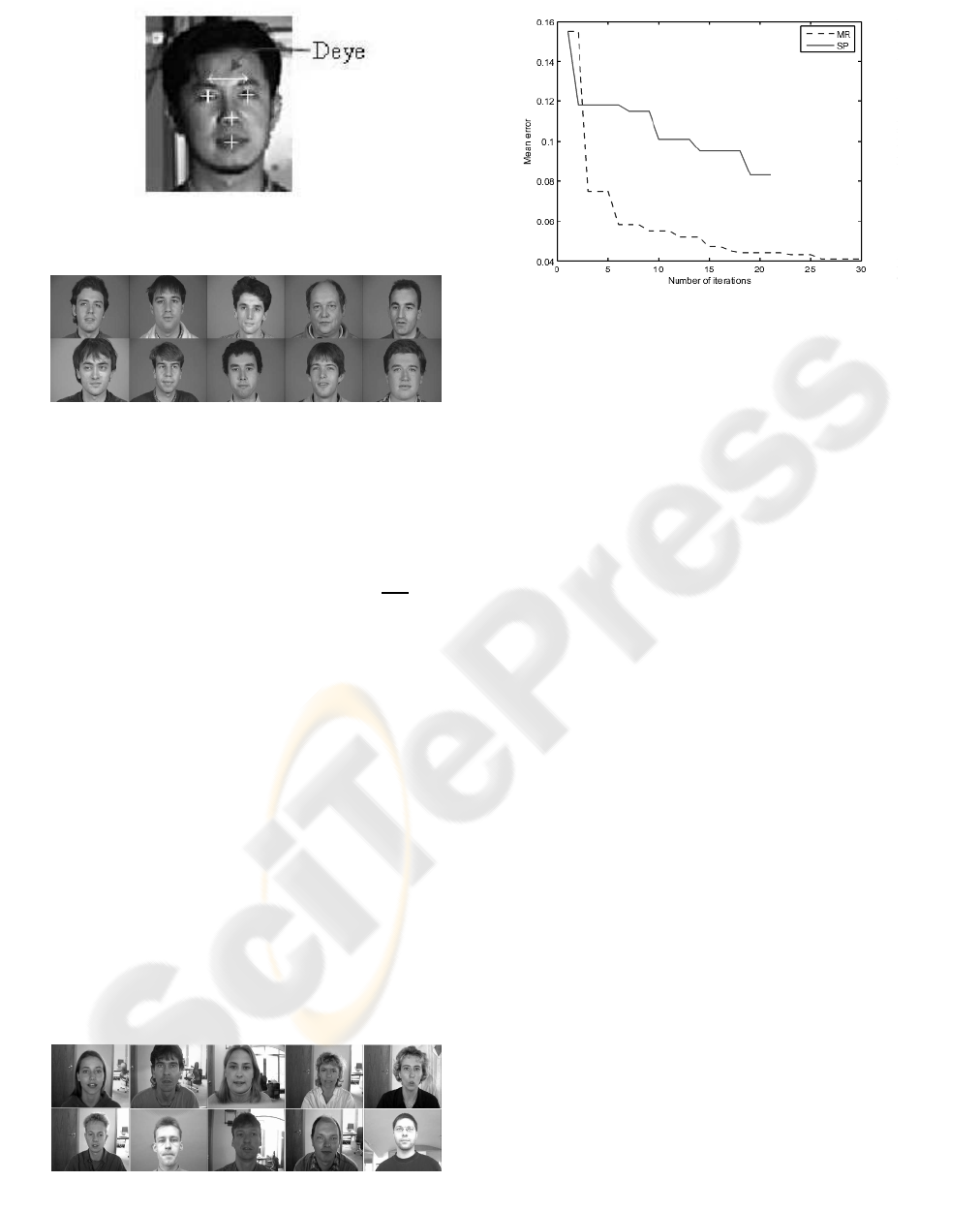
Figure 1: D

eye

distance.

Figure 2: Learning data base from M2VTS.

of point of marking of the i part. The algorithm con-

verges when the 3 errors were lower than convergence

threshold. The threshold was calculated according to

the distance between the eyes. In these tests we have

taken the threshold of convergence equal to

eye

(Fig.

1). That guarantees a rather precise convergence.

Number of iterations: In order to compare SP

optimization with that of RM, we need to ﬁx the

minimum number of iterations needed by AAM to

converge. With this intention we have tested the

AAM on the 10 faces of BioID by ﬁxing the number

of iteration at 30 for shift of t

= −4 pixels. Only

the images on which the AAM converged were taken

into the account. From it we deduce a curve of

convergence of the quadratic errors between pixels

(minimized error) from the successfully converged

images. The curve of ﬁgure 4 shows the number

of iterations required by AAM to converge, at the

bottom of an error of 0.05 the AAM have converged

with 18 iterations in our case. The average of curve

is made on the curves belonging to the images

where our algorithm have converged. The realized

curve of convergence compared to the number of

Figure 3: Test data base from BioID.

Figure 4: Mean of convergence curve of algorithm using

RM and SP.

iterations is shown in ﬁgure 4. The comparison of

the two curves shows that the error obtained by RM

(≈ 0.05) is lower than that found by SP ≈ 0.094.

The minimum of this error is not always a good

adjustment of the model on the true face in test image

and depends much on initialization. Even if the SP

found higher error, it presents better results in term

of marking error. That is illustrated in the ﬁgure 6.

The initialization has an inﬂuence on the minimum

of the function error reached by each algorithm of

optimization. Figure 7 presents the results obtained

by an initialization on the true face (t

= 0, t

= 0,

true scale

true orientation

) comparing

convergence in error of marking and pixels. It shows

that optimization by SP gives better results in terms

of pixels and marking in the case of a favorable

initialization.

Robustness on initialization: Knowing that our al-

gorithm convergesunder the same conditions (an even

number of error calculation), we plot the curve of con-

vergence expressed as a percentage of converged im-

ages compared to displacements in t

. So to remove

random aspect of SP initialization, we did 10 simplex

and we obtained mean curve of convergence. Figure

5 represents a comparison between the realized curve

and that obtained by RM.

Figure 5 shows also that SP optimization has same

capacities of convergence in the most favorable case

(the case where initialization is on the true face) while

having the same number of error calculation. The use

of Nelder Mead algorithm as an optimization method

of AAM allows being more robust than RM in term of

initialization. Even starting in far initialization we ob-

tain better results than the RM. The difﬁculty to align

unknown faces is caused by the initialization (Eq. 2).

In the learning phase the error is generated by c

(true

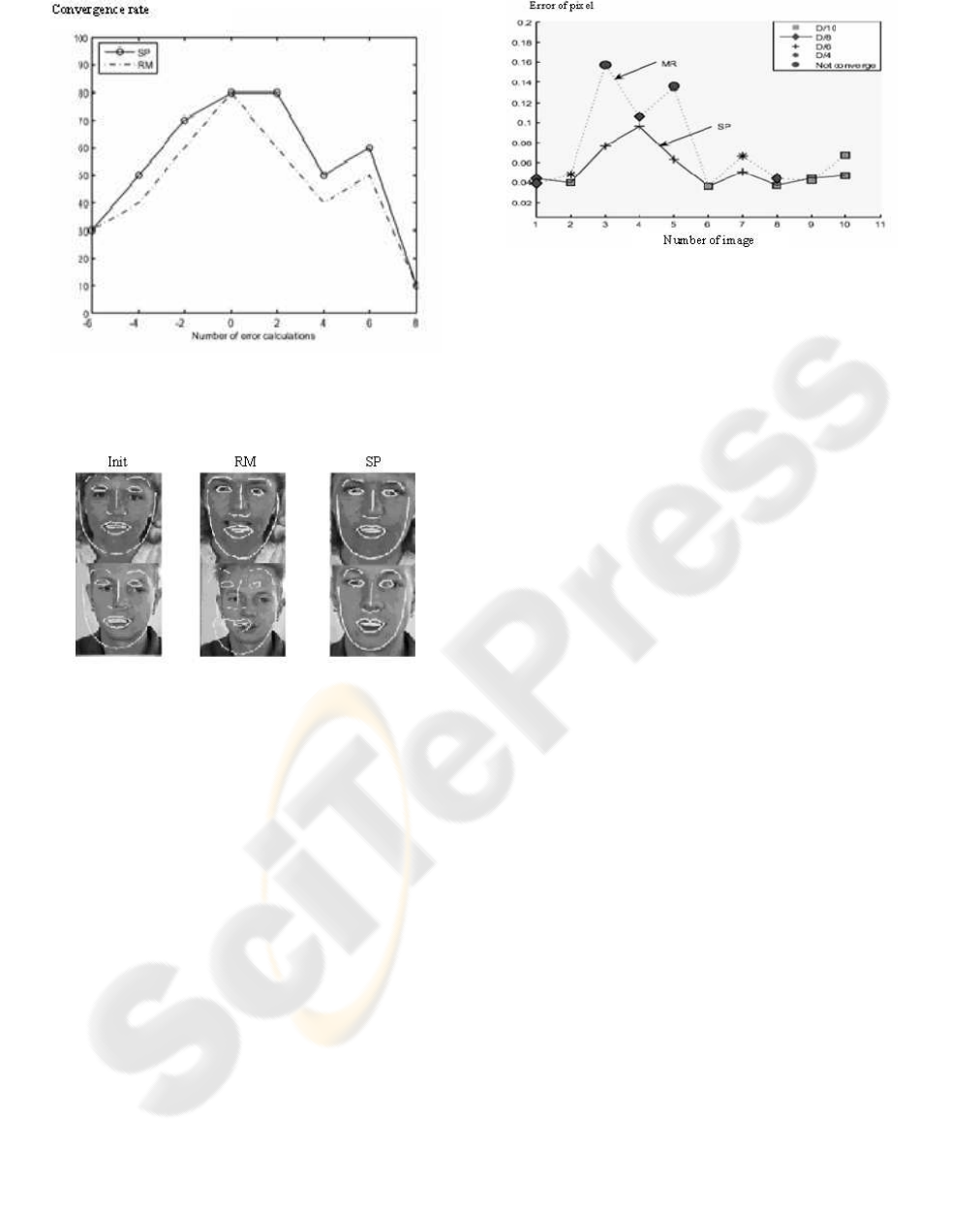
Figure 5: Comparison between convergence rate of RM and

SP in terms of marking error in different translation initial-

ization.

Figure 6: Results obtained on faces with RM (middle) and

SP (right).

face model parameters). In (Eq. 4) the new shapes are

generated from modiﬁcations of δc on vector repre-

senting the true face c

. Whereas research in segmen-

tation phase is initialized by using mean shape and

texture. If faces contained in test data base are differ-

ent than faces belonging to learning data base, the RM

present difﬁculty to predict the appropriate modiﬁca-

tions. In the case of the Nelder Mead optimization

there is several initialization which can converge to

the true face by non linear changes of solutions.

The results obtained in ﬁgure 6 show the capacity

of the SP to ﬁnd solutions which converge toward the

true face while having a higher degree of accuracy

comparing with RM.

5 CONCLUSION

The reduction of necessary memory space on embed-

ded technologies required to use algorithms which are

Figure 7: Results obtained on faces initialized by t

= 0

using RM et SP by highlighting convergence by distance

eye.

greedy in the requirement data storage for system be-

havior. We proposed to use Nelder Mead algorithm

instead of RM optimization in the segmentation phase

of AAM. It allows us to save 73% of the memory used

by the classical AAM while being more robust in ini-

tialization compared to initialization of the model.

THANKS

This research was supported by Brittany Region (”re-

gion de bretagne”) in France.

REFERENCES

BioID. Biometric identity data base, www.bioid.com.

Cristinacee, D. and Cootes, T. (2004). A comparaison of

shape constrained facial feature detectors. pages 375–

380.

G. J. Edwards, C. J. Taylor, T. F. C. (1998). Interpreting

face images using active appearance models.

Hu, C., Feris, R., and Turk, M. (2003). Active wavelet net-

works for face alignment.

NELDER, J. A. and MEAD, R. (1965). A simplex method

for function minimization. volume 7, pages 308–313.

PIGEON, S. (1996). www.tele.ucl.ac.be.

Stegmann, M. (2000). Active appearance models theory,

extension and cases.

T. Cootes, P. K.-n. (2002). Comparing variations on the

active appearance model algorithm. pages 837–846.

X. Hou, Stan Z. Li, H. Z. and Cheng, Q. (2001). Direct

appearance models.