DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH
GENETIC ALGORITHMS FOR GLOBAL OPTIMIZATION
Nam-Geun Kim, Youngsu Park and Sang Woo Kim
Division of Electrical and Computer Engineering, Pohang University of Science and Technology (POSTETH), Pohang, Korea
Keywords:
Global optimization, Genetic algorithms, Pattern search.
Abstract:
In this paper, we present a new evolutionary algorithm called genetic pattern search algorithm (GPSA). The
proposed algorithm is closely related to genetic algorithms (GAs) which use binary-coded genes. The main
contribution of this paper is to propose a binary-coded pattern called digital pattern which is transformed from
the real-coded pattern in general pattern search methods. In addition, we offer a self-adapting genetic algo-
rithm by adopting a digital pattern that modifies the step size and encoding resolution of previous optimization
procedures, and chases the optimal pattern’s direction. Finally, we compare GPSA with GA in the robust-
ness and performance of optimization. All experiments employ the well-known benchmark functions whose
functional values and coordinates of each global minimum have already been reported.
1 INTRODUCTION
Global optimization has attracted much attention re-
cently (Horst and Pardalos, 1995; Pardalos et al.,
2000; Pardalos and Romeijn, 2002), because of a
wide spectrum of applications in real-world systems.
Global optimization refers to finding the extreme
value of a given function in a certain feasible region,
and such problems are classified in two classes; un-
constrained and constrained problems. This paper
concerns a class of optimization algorithms that can
be applied to bound constrained problems
min f(x) : R
n
→ R, (1)
subject to x ∈ R
n
,
l
i
≤ x
i
≤ u
i
, i = 1,··· ,n,
where l
i
, u
i
∈ R and l
i
< u
i
.
Although the works that deal with the global opti-
mization are still not enough, they manage to confront
the rapid growth of applications. And such work have
yielded new practical solvers for global optimiza-
tion, called meta-heuristics. The structures of meta-
heuristics are mainly based on simulating nature and
artificial intelligence tools (Osman and Kelly, 1996).
Genetic algorithms (GAs) are one of the most effi-
cient meta-heuristics (Goldberg, 1989; Michalewicz,
1996), that have been employed in a large variety of
problems. However, most meta-heuristics including
GAs suffer from slow convergence that brings about
heavy computational costs mainly because they may
fail to detect promising search directions, especially
in the vicinity of local minima owing to their random
constructions.
Combining meta-heuristics with local search
methods is a practical solution in overcoming the
drawbacks of slow convergence and random con-
structions of meta-heuristics. In these hybrid meth-
ods, local search strategies are included inside meta-
heuristics to guide them in the vicinity of local min-
ima, and to overcome their slow convergence espe-
cially in the final stage of the search. This paper pur-
sues that approach and proposes a new hybrid algo-
rithm that combines GAs with a new pattern search
method. Pattern search methods are a class of di-
rect search methods that require neither explicit nor
approximate derivatives. Abstract generalizations of
pattern search methods have been provided in (Torc-
zon, 1997; Audet and Dennis, 2003). We will adopt
a new idea in pattern search to form a hybrid algo-
rithm. The new pattern search method, called digital
pattern search (DPS) method, digitizes the patterns of
pattern search methods into binary-codes. Thus, we
380
Kim N., Par k Y. and Woo Kim S. (2007).
DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH GENETIC ALGORITHMS FOR GLOBAL OPTIMIZATION.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 380-387
DOI: 10.5220/0001650903800387
Copyright
c
 SciTePress

can easily combine GAs and pattern search method to
construct a global search method called genetic pat-
tern search algorithm (GPSA).
There have been some attempts to utilize the idea
of hybridizing local search methods with GA. Simple
hybrid methods use the GAs or local search methods
to generate the points for new population and then
apply other techniques to improve this new popula-
tion (G
¨
unal, 2000; Zentner et al., 2001). Other hy-
brid methods do some modifications in the GA oper-
ations; selection, crossover and mutation using local
search methods (Musil et al., 1999; Yang and Dou-
glas, 1998; Yen et al., 1998; Hedar and Fukushima,
2004). However, the method proposed in this paper is
different from these hybrid methods in many aspects.
One of the main differences lies in the coding repre-
sentation. We use the DPS methods in which digital
patterns are binary-coded genes, and it is capable of
using the evolutionary operators in GAs without mod-
ifications. Another significant difference is the self-
adapting genetic algorithms that modify the step size
and chase the approximate optimal direction by using
local information from digital patterns. Numerical re-
sults from well-known benchmark functions indicate
that GPSA exhibits a very promising performance in
obtaining the global minima of multimodal functions.
In the remainder of the paper, we briefly review
the basics of GAs and pattern search methods in Sec-
tion 2. Section 3 proposes the DPS methods. The
description of the main GPSAs is given in Section 4.
In Section 5, we show experimental results. Finally,
the conclusion is given in Section 6.
Notation. Let B, R, Q and Z denote the sets of bi-
nary, real, rational and integer numbers, respectively.
All norms will be Euclidean vector norms or the as-
sociated operator norm.
2 BACKGROUND
In this section, we will give a brief description of GAs
and pattern search methods. Both of them only use
the function values rather than derivatives, and they
can be used for problems with discrete design param-
eters. However, they are different in the coding repre-
sentation. GAs use binary-coded genes, while pattern
search methods use real-coded (floating-point) genes.
We propose a digital pattern in order to hybridize GAs
and pattern search methods.
2.1 Genetic Algorithms
GAs are algorithms that operate on a finite set of
points, called a population. The population consists
of the m bit string s
i,m
= [b
i,m
,·· · , b
i,1
], where b ∈ B
and i ∈ {1,··· ,n}, which can be interpreted as the en-
coding of a vector x ∈ R
n
for problem (1).
GAs are derived on the principles of natural selec-
tion and they incorporate operators for fitness assign-
ment, selection of points for recombination, recombi-
nation of points, and mutation of a point.
The pseudo code in Figure 1 describes the steps
executed in a general GA.
Randomly generate an initial population P(0) :=
{S
1
(0),··· ,S
µ
(0)} where S(t) = [s
n,m
,··· ,s
1,m
].
Determine the fitness of each individual.
Repeat t = 1, 2, · · ·
Perform recombine with probability p
r
.
Perform mutation with probability p
m
.
Determine the fitness of each individual.
Perform replacement with an elitist replacement
policy.
Until some stopping criterion is satisfied.
Figure 1: Pseudo code of general GA.
GAs start by generating an initial population P(0)
of µ randomly generated points S(0). Then, the fit-
ness values are evaluated for each point in P(0). The
fitness of a point indicates the worth of the point in
relation to all other points in the population. The se-
lected points are recombined to a new pair of points.
In recombination, the crossover position is randomly
selected with a probability of p
r
∈ [0,1] and the bits
after this position are exchanged between the two
points. Each recombined point is mutated by a mu-
tation, which changes the value of some bits of the
binary strings with a probability of p
m
∈ [0,1]. After-
wards, replacement selects the µ
e
fittest points (0 <
µ
e
< µ) of the generation as the elite set. These points
will be put in the next generation.
2.2 Pattern Search Methods
According to (Audet and Dennis, 2003), pattern
search methods have common things after a finite
number of iteration. They search for a cost function
value lower than that of the current iterate x
k
on the
trial points in the poll set
L
k
= {x
k
+ ∆
k
p
k
, p
k
∈ P
k
}, (2)
where ∆
k
> 0 is a step size, and a pattern p
k
is the
columns of the pattern matrix P
k
defined in (Torczon,
1997). The pattern matrix is decomposed into a basis
matrix B ∈ R
n×n
and a generating matrix C
k
∈ Z
n×p
,
p > 2n. Restrictions onC
k
guarantee that the columns
of BC
k
span R
n
. Conceptually, the generating matrix
DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH GENETIC ALGORITHMS FOR GLOBAL
OPTIMIZATION
381

defines the search directions, while the basis matrix
rotates and scales the search directions to determine
the coordinate system used during the search.
In addition, each PS method has a rule called
search step (Audet and Dennis, 2003) that selects a
finite number of points on a mesh defined by
M
k
= {x
k
+ ∆
k
P
k
z, z ∈ Z
p
}. (3)
At iteration k, the mesh is centered around the current
iterate x
k
, and its fineness is parameterized through
the step size ∆
k
. The search step strategy that gives
the set of points is usually provided by the user; it
must be finite and the set can be empty.
The pseudo code in Figure 2 describes the main
elements of a pattern search method. It is based on
the method presented in (Audet and Dennis, 2003).
Let the initial solution x
0
∈ R
n
and step length ∆
0
be
given.
Repeat k = 1,2,···
Perform the Search Step:
Evaluate f on a finite subset of trial points on
the mesh M
k
defined by (3).
Perform the Poll Step:
Evaluate f on the poll set defined by (2).
Update the pattern matrix and ∆
k
.
Until some stopping criterion is satisfied.
Figure 2: Pseudo code of pattern search method.
The scenario of a pattern search method starts with
fitting the initial solution, and then two search stages
are invoked. The first staged is a search step in which
any search procedure can be defined by the user to
generate trial points from M
k
. The main role of the
search step is to achieve faster convergence of pat-
tern search method. The other stage called poll step is
performed as a systematic search in order to exploit a
region around the current solution. If the search step
and poll step fail to produce a trial step that gives a
simple decrease, then the step size is reduced to refine
the mesh. Otherwise, the step size is increased or pre-
served. The pattern search method may be terminated
when the step size becomes small enough.
3 DIGITAL PATTERN SEARCH
METHOD
In this section, we propose the digital pattern search
(DPS) method before introducing genetic pattern
search algorithm (GPSA). This section formulates the
abstraction of DPS methods. The definitions and the
(a) (b) (c)
Figure 3: Trial points generated by some kinds of digital
patterns. Ash-colored bulbs are trial points. (a), (b), and (c)
correspond to digital patterns of compass search, evolution-
ary operation using factorial designs and coordinate search,
respectively.
algorithm for generalized DPS methods follow de-
scriptions of pattern search methods provided in (Tor-
czon, 1997) and (Audet and Dennis, 2003).
3.1 Digital Pattern
Adding 0 or 1 to an existing binary string as a least
significant bit (LSB) can be interpreted as generating
trial points of pattern search methods. The decoded
real number of a new binary string that is appended
LSB ”0” is decreased and that is appended LSB ”1” is
increased than that of the original binary string. This
property is adopted as pattern to generate trial points
which are solution candidates. Figure 3 depicts the
2 bit string’s trial points that are presented by binary
strings or binary matrices in which each row repre-
sents an encoded string for the corresponding param-
eter.
Pattern search methods can be divided by pattern
matrix P
k
into a compass search, evolutionary oper-
ation, coordinate search, and so on (Torczon, 1997).
Digital pattern can describe some kinds of patterns
according to whether or not an LSB is attached to
each dimension of bit strings. Figure 3 depicts some
kinds of digital patterns that mimic pattern of com-
pass search, pattern of evolutionary operation using
factorial designs, and pattern of coordinate search, re-
spectively.
The DPS method requires a mechanism for de-
coding from each m-bit string s
i,m
= [b
i,m
,·· · , b
i,1
] to
the corresponding object variable x
i,m
. According to
the standard binary decoding function f
d
: {0,1}
m
→
[u
i
,v
i
], where (Michalewicz, 1996), the real value is
x
i,m
= f
d
(s
i,m
) = u
i
+
v
i
− u
i
2
m
− 1
m−1
∑
j=0
b
i,( j+1)
2
j
. (4)
If 0 is added to the LSB of s
i,m
, let the new string
be termed a 0-bit child string, s
0
i,m+1
. On the other
hand, if 1 is added, it is termed a 1-bit child string,
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
382

Figure 4: Biased binary tree structure together with corre-
sponding normalized real values in parenthesis.
s
1
i,m+1
. And the real values of the child strings are
x
0
i,m+1
=
u
i
2
m+1
− 1
+
2
m+1
− 2
2
m+1
− 1
x
i,m
,
x
1
i,m+1
=
v
i
2
m+1
− 1
+
2
m+1
− 2
2
m+1
− 1
x
i,m
.
The Difference between a parent string and each child
string implies the step size ∆
k
in pattern search meth-
ods. For a given parent string x
i,m
, the comparison be-
tween the distances of |x
0
i,m+1
−x
i,m
| and |x
1
i,m+1
−x
i,m
|
is given by
| x
1
i,m+1
− x
i,m
| − | x
0
i,m+1
− x
i,m
|=
(v
i
− u
i
) − 2x
i,m
2
m+1
− 1
.
(5)
From (5), the differences between two step sizes vary
according to the position of the parent string in the
finite intervals [u
i
,v
i
].
In Figure 4, the property in (5) is clearly visual-
ized in the form of binary trees whose nodes are repre-
sented by binary strings and their corresponding real
numbers. Owing to the specific property of digital
pattern that increases the bit length of binary strings,
the standard binary decoding function (4) has a bi-
ased search tendency to incline its steps toward the
middle point of the finite intervals [u
i
,v
i
] depending
on the location of a parent string. Therefore, we need
a more suitable binary decoding function for digital
pattern and the unbiased binary decoding function is
designed as:
x
i,m
= u
i
+
v
i
− u
i
2
m+1
m−1
∑
j=0
b
j
2
j+1
+1
!
,
and the real values of the child strings are given as:
x
0
i,m+1
= x
i,m
−
v
i
− u
i
2
m+2
, x
1
i,m+1
= x
i,m
+
v
i
− u
i
2
m+2
. (6)
Both step sizes are the same, (v
i
− u
i
)/ 2
m+2
. Figure
5 shows that the unbiased binary decoding function
guarantees the symmetric search property.
To define digital pattern, we treat bit strings with
the decoded real value defined in the iterative form
Figure 5: Unbiased binary tree structure together with cor-
responding normalized real values in parenthesis.
(6). According to (6), the real values of trial points
are analogous to the description of generalized pattern
search methods in (Torczon, 1997). A basis matrix
can be defined a nonsingular matrix B ∈ R
n×n
B = diag(l
1
,.. . ,l
n
) = diag(u
1
− v
1
,.. . ,u
n
− v
n
),
where diag(·) is a diagonal matrix. B represents the
intervals of each dimension of x. A generating ma-
trix C ∈ Z
n×p
, where p > 2n, contains in its columns
combinations of {1,0,−1}, except for the column of
zeros. For example, when digital pattern for coordi-
nate search is executed for n = 2, we have a generat-
ing matrix such as
C =

1 0 −1 0 1 1 −1 −1
0 1 0 −1 1 −1 −1 1

.
It can be seen in Figure 3 (c).
Digital pattern p is then defined by the columns
of the digital pattern matrix P = BC. Because both B
and C have the rank n, the columns of P span R
n
. The
step size ∆
m
is defined as ∆
m
=
1
2
m
under the given
bit string length m. Thus the poll set composed of
points neighboring the current x
m
in the directions of
the columns of C is expressed as
L
m
= {x
m
+
1
4
∆
m
p, p = Bc and c ∈ C}.
Among them, the best one is chosen by evaluation as
an optimal solution of L
m
, x
∗
m+1
= x
m
+
1
4
∆
m
Bc
∗
m+1
,
where c
∗
m+1
is the column of C as a direction vector
pointing the search direction toward the optimal solu-
tion.
3.2 Digital Step
Using the standard binary representation, the DPS
method can get caught on a “Hamming cliff”, be-
ing confined to the barrier of binary branches. For
example, if the DPS method is started at the high-
est node of “0” in the tree, it can never escape from
the left half plane of parameters. Digital step in the
DPS method is employed to avoid such problems. If
a binary string undergoes increment addition (INC)
DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH GENETIC ALGORITHMS FOR GLOBAL
OPTIMIZATION
383

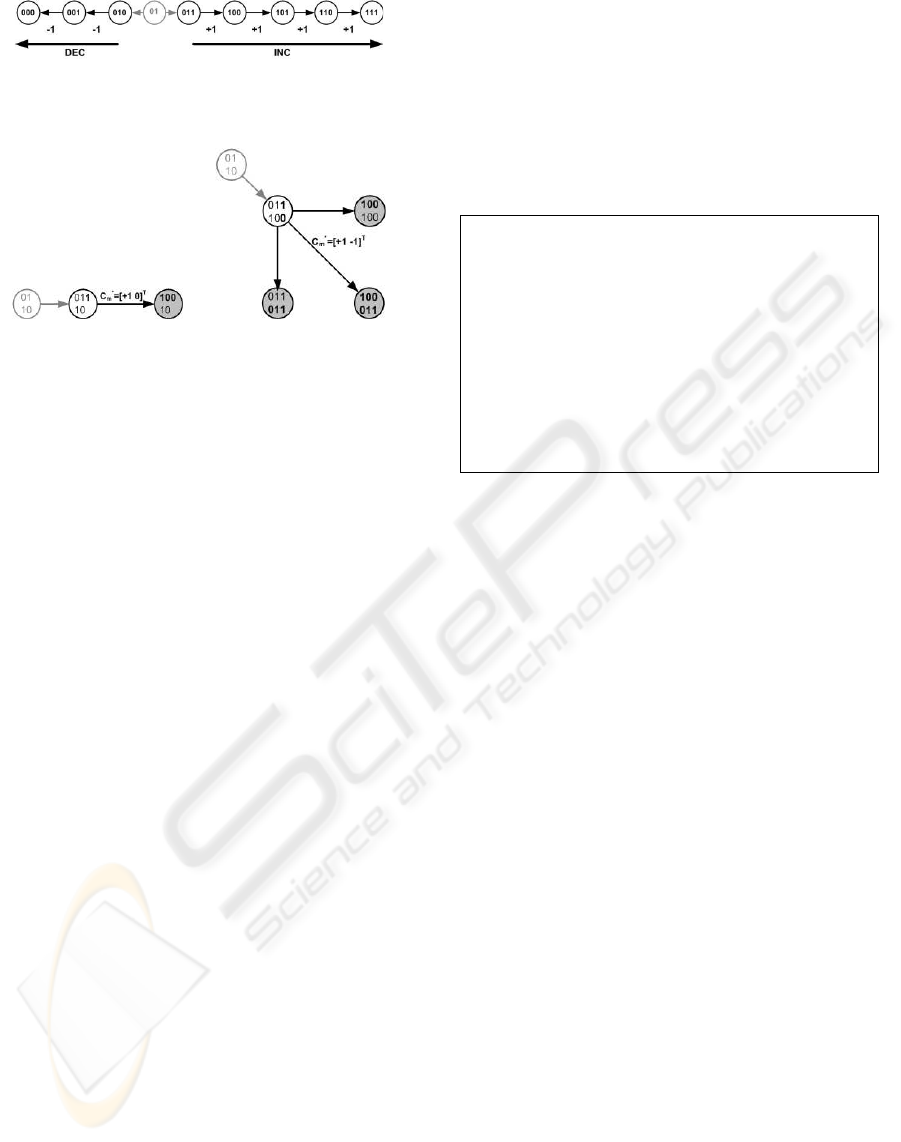
Figure 6: Process of digital step. in one dimensional dia-
gram.
(a) (b)
Figure 7: Process of digital step. in two dimensional dia-
gram. (a) and (b) correspond to the results depended on c
∗
m
,
[+1 0]
T
and [+1 − 1]
T
, respectively.
or decrement subtraction (DEC), the real number of
each processed string increases or decreases. Through
the simple operations of INC and DEC for binary
strings, digital step can readily remove the barrier be-
tween any binary trees and broadly search the effec-
tive area that has a high possibility of finding the op-
timal solution. Figure 6 illustrates the process of digi-
tal step (if direction vector is 1, then INC is executed,
otherwise DEC is achieved).
In digital step, the objective function f is eval-
uated at a finite number of points on a mesh to try
to find a point that yields a lower objective function
value than the current point. The basic component in
the definition of digital step is the mesh. The mesh is
a discrete subset of R
n
whose fineness is parameter-
ized by the step size ∆
m
as follows:
M
m
= {x
∗
m
+ ∆
m
diag(z)Bc
∗
m
: z ∈ Z
n
},
where diag(·) is a diagonal matrix, z is the vector of
nonnegative integers and c
∗
m
is a direction vector cho-
sen by evaluation of poll set. This way of describ-
ing the mesh is different from the form in (Audet
and Dennis, 2003). This specific sub-technique of the
DPS method attempts to accelerate the progress of the
algorithm by exploiting the information gained from
the search.
The trial points generated by digital step are de-
cided by a sort of digital patterns. Figure 7 shows the
examples of digital step in a two dimensional search
space. INC or DEC is selected by c
∗
m
from the pre-
vious digital pattern. Then digital step continues to
search in the trial points which are generated by per-
forming INC or DEC at each dimension. Generation
of the trial points by the digital pattern is executed
one time, while generation of the trial points by dig-
ital step continues until a local minimum is attained
on the same bit mesh.
3.3 Digital Pattern Search Method
The pseudo code in Figure 8 describes the proposed
digital pattern search method.
Set an initial row length α and a final row length β.
Randomly generate an initial binary matrix Γ
n×α
.
for each low length m = α : β do
1. Perform the Digital Pattern.
2. Evaluate trial points and determine a direction
vector.
3. while (a better solution is attained) do
(a) Perform the Digital Step.
(b) Evaluate trial points.
end while
end for
Figure 8: Pseudo code of digital pattern search method.
The basic structure of the DPS method consists of
two asynchronous loops. The outer loop (steps 1-3)
selects the best trial point generated by digital pat-
tern and hands over a direction vector to digital step.
The inner loop (step 3) conducts finite searches in the
guided direction vector until the consecutive digital
step fails to make progress. When this occurs a local
minimum of a session is found; the inner loop then
terminates and the outer loop starts the next session.
At steps 1 and 3(a), digital pattern and digital step
generate n×m binary matrices as trial points, i.e., one
of the matrices Γ
n×m
implies that each row n repre-
sents an encoded string for the corresponding param-
eter, and that the row length m is exponentially pro-
portional to the resolution of parameters. To evaluate
trial points in steps 2 and 3(b), each row of Γ needs
to be converted to the real number using a binary de-
coding function. After evaluation in step 2, the least
significant column of the best trial point is appointed
the direction vector which is handed over to digital
step for further exploration.
4 GENETIC PATTERN SEARCH
ALGORITHM
GPSA uses the main operations of GA; recombina-
tion, mutation, and replacement, on a population to
encourage the exploration process. Moreover, the
GPSA tries to improve the new children by applying
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
384

DPS method. Figure 9 shows the pseudo code de-
scribing GPSA.
Set an initial row length α and a final row length β.
Set an GA’s generation number N.
Randomly generate an initial population P
α
(0) :=
{Γ
1
n×α
(0),··· ,Γ
µ
n×α
(0)}
Determine the fitness of each individual.
for each low length m = α : β do
for GA’s generation k = 0 : N do
Perform recombine with probability p
r
.
Perform mutation with probability p
m
.
Compute the fitness of each individual.
Perform replacement with an elitist replace-
ment policy.
end for
Perform the Digital Pattern.
Compute the fitness of trial points of each indi-
vidual and determine a direction vector.
while a better solution is attained do
Perform the Digital Step.
Compute the fitness of trial points of each in-
dividual.
end while
Perform replacement with an elitist replacement
policy.
end for
Figure 9: Pseudo code of GPSA.
The GPSA starts by generating an initial popu-
lation P(0) of µ randomly generated points Γ which
is composed by α bit-length strings. The inner loop
in GPSA incorporates GA operators: recombina-
tion, mutation, and replacement. In recombination, a
crossover position is randomly selected with a proba-
bility of p
r
∈ [0,1]. Each recombined point is mutated
with a probability of p
m
∈ [0,1]. Replacement selects
the µ
e
fittest points (0 < µ
e
< µ) of the generation as
the elite set. After N times iterations of the inner
loop, the DPS method is applied to the points gen-
erated by the evolutionary operators and constructs
each sequence of iterates that converge to a station-
ary point on the mesh parameterized by the step size
∆
m+1
. The restriction on the replacement strategy en-
sures that the elite set is kept for further processing.
5 EXPERIMENTAL RESULTS
This section presents a performance comparison of
the GPSA and the conventional GA on the well-
known 8 benchmark functions whose functional val-
ues and coordinates of each global minimum are al-
ready reported in (Yao et al., 1999; Schwefel, 1995).
Several kinds of benchmark functions are selected to
make a generalized conclusion: functions with no lo-
cal minima ( f
1
-f
2
) and local minima ( f
3
-f
8
). A more
detailed description of each function is given in the
Appendix.
5.1 Experimental Setup
For both GA and GPSA tests, we used a population
size µ of 10 with the elite set µ
e
= 1, and for each
problem the number of trials was 100. The recombi-
nation operator was uniform crossover with a prob-
ability p
c
= 0.5, and the mutation probability was
p
m
= 0.001. The length per object variable in GA
was 10, and in GPSA, the initial and final low length
per object variable were α = 3 and β = 10, respec-
tively. The number of generations was 4,000 in GA
and N = 50 in GA loop of GPSA.
To implement GPSA, it is necessary to deter-
mine a proper kind of the generating matrix in dig-
ital pattern. We used the standard 2n directions,
C = {e
1
,·· · , e
n
,−e
1
,·· · , −e
n
}, where e
i
∈ R
n
is the
i−th unit vector, because it gives a linear increase of
function evaluation with problem dimension.
GA was terminated after 40,000 function eval-
uations, and the performance comparisons between
GPSA and GA were made based upon the termina-
tion point of GPSA. Our experimental analysis con-
siders three performance measures: the number of
trials which succeed in attaining to the global opti-
mum for each benchmark function, the number of cost
function evaluations during simulations, and the value
of the best solution found.
5.2 Numerical Results
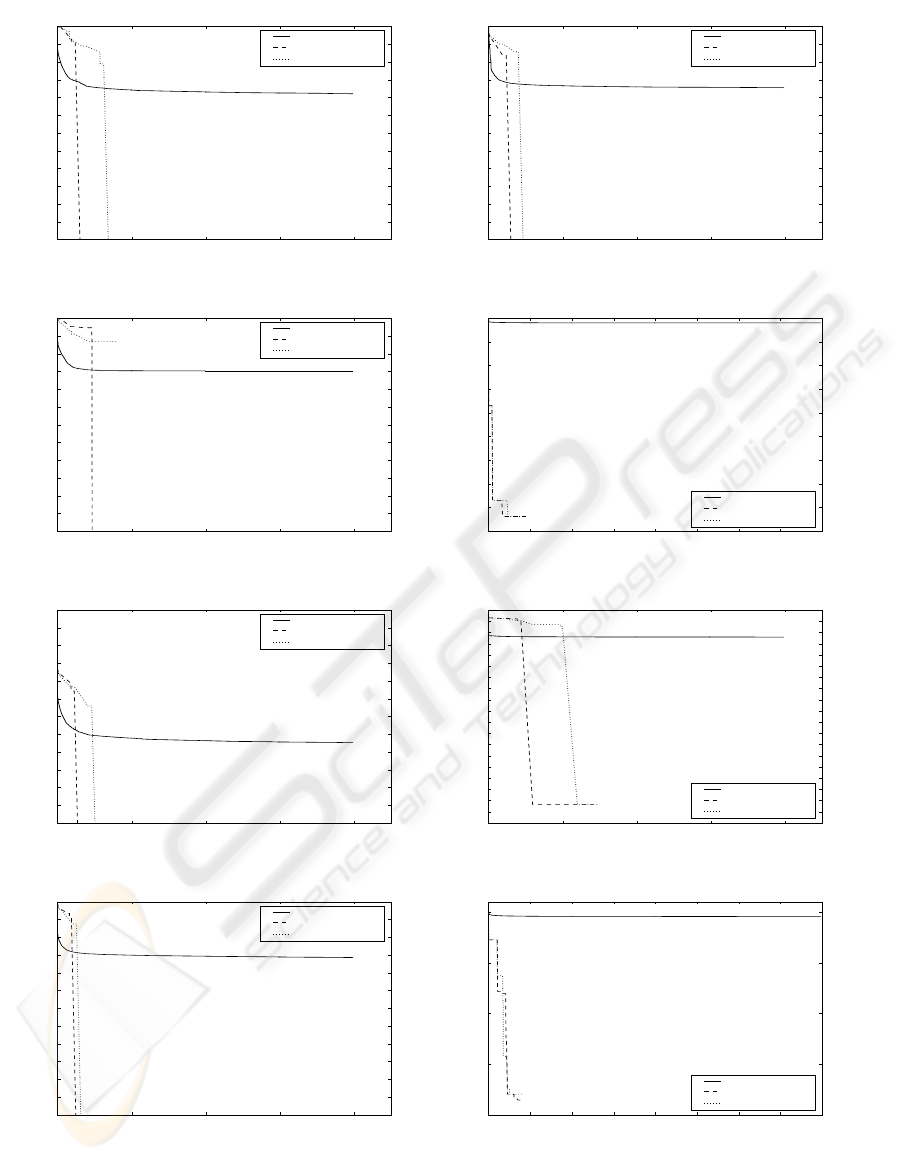
Figure 10 shows the performances of GPSA and GA
on the benchmark functions. The results of GPSA
were selected through 100 independent trials as the
best case and the worst case, and the result of GA was
averaged over 100 independent trials. The GA con-
verged faster than the GPSA for most functions ini-
tially, around 4,000 to 6,000 of function evaluations.
However, GPSA overperformed GA obviously while
fewer function evaluations. Although GA quickly ap-
proaches the neighborhood of the global minimum,
GA has a difficulty in obtaining some required accu-
racy. DPS method’s ability to accelerate the search
and to refine the solution more evenly helps GA in
achieving good performance.
To judge the success of a trial, we used the condi-
tion
| f
∗
−
ˆ
f| < ε
1
| f
∗
| + ε
2
,
DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH GENETIC ALGORITHMS FOR GLOBAL
OPTIMIZATION
385

Table 1: Results of GPSA. The results were averaged over
100 independent trials where “SUCC %” indicates the ra-
tio of trials which succeed in attaining the global optimum
, “EVAL #” means the average number of function eval-
uations, and “VAR” means the variance of trials which
succeed. Functions (Yao et al., 1999; Schwefel, 1995):
SP (spare function), SC1 (schwefel’s problem 2.22), SC2
(schwefel’s problem 1.2), SC3 (schwefel’s problem 2.26),
GR (griewank function), AC (ackley function), RA (rastrign
function), and SH (shubert function). And “n” is the num-
ber of variables.
Function SUCC % EVAL # VAR
SP (n = 10) 100 5504.35 0.0
SC1 (n = 10)
100 4773.82 0.0
SC2 (n = 10)
44 5635.07 0.0
SC3 (n = 2)
92 2116.56 0.0
GR (n = 10)
100 5321.53 0.0
AC (n = 10)
100 5483.51 0.0
RA (n = 10)
92 7590.75 0.0
SH (n = 2)
38 4240.23 0.0013
where
ˆ
f refers to the best function value obtained by
GPSA, f
∗
refers to the known exact global minimum,
and ε
1
and ε
2
are small positive numbers. We set ε
1
and ε
2
equal to 10
−3
and 10
−6
, respectively. The re-
sults are shown in Table 1, where the average number
of function evaluations and the variance are related
only to successful trials. Table 1 shows that GPSA
reached the global minima in a very good success rate
for the majority of the tested functions. Moreover, the
numbers of function evaluations and the average er-
rors show the efficiency of the method.
On the other hands, GA had few successful tri-
als on any test functions at the termination point of
GPSA.
6 CONCLUSIONS
This paper first developed a new class of pattern
search method that digitizes the patterns, called the
digital pattern search (DPS) method. Then, we pre-
sented a new hybrid global search algorithm, the ge-
netic pattern search algorithm (GPSA), which has a
self-adapting technique to modify the step size and
chase the approximate optimal direction. Applying
the DPS method in addition to the ordinary GA oper-
ators such as recombination and mutation enhances
the exploration process and accelerates the conver-
gence of the proposed algorithm. The experimental
results also showed that the GPSA works successfully
on some well known test functions.
REFERENCES
Audet, C. and Dennis, Jr., J. E. (2003). Analysis of general-
ized pattern searches. SIAM J. on Optim., 13(3):889–
903.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley,
Boston, MA.
G
¨
unal, T. (2000). A hybrid approach to the synthe-
sis of nonuniform lossy transmission-line impedance-
matching sections. Microwave and Optical Technol-
ogy Letters, 24:121–125.
Hedar, A. and Fukushima, M. (2004). Heuristic pattern
search and its hybridization with simulated annealing
for nonlinear global optimization. Optim. Methods
and Software, 19:291–308.
Horst, R. and Pardalos, P. M. (1995). Handbook of Global
Optimization. Kluwer Academic Publishers, Boston,
MA.
Michalewicz, Z. (1996). Genetic algorithms + data struc-
tures = evolution programs. Springer-Verlag, London,
UK.
Musil, M., Wilmut, M. J., and Chapman, N. R. (1999).
A hybrid simplex genetic algorithm for estimating
geoacoustic parameters using matched-field inversion.
IEEE J. Oceanic Eng., 24(3):358–369.
Osman, I. H. and Kelly, J. P. (1996). Meta-Heuristics: The-
ory and Applications. Kluwer Academic Publishers,
Boston, MA.
Pardalos, P. M. and Romeijn, H. E. (2002). Handbook of
Global Optimization. Kluwer Academic Publishers,
Boston, MA.
Pardalos, P. M., Romeijn, H. E., and Tuy, H. (2000). Recent
developments and trends in global optimization. J.
Comput. Appl. Math., 124(1-2):209–228.
Schwefel, H.-P. (1995). Evolution and Optimum Seeking:
The Sixth Generation. Addison-Wesley, New York,
NY.
Torczon, V. (1997). On the convergence of pattern search
algorithms. SIAM J. on Optim., 7(1):1–25.
Yang, R. and Douglas, I. (1998). Simple genetic algorithm
with local tuning: efficient global optimizing tech-
nique. J. Optim. Theory Appl., 98(2):449–465.
Yao, X., Liu, Y., and Lin, G. (1999). Evolutionary pro-
gramming made faster. IEEE Trans. on Evol. Com-
put., 3(2):82–102.
Yen, J., Liao, J., Randolph, D., and Lee, B. (1998). A hy-
brid approach to modeling metabolic systems using a
genetic algorithm and simplex method. IEEE Trans.
on Syst., Man, and Cybern. B, 28(2):173–191.
Zentner, R., Sipus, Z., and Bartolic, J. (2001). Optimization
synthesis of broadband circularly polarized microstrip
antennas by hybrid genetic algorithm. Microwave and
Optical Technology Letters, 31:197–201.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
386

0 1 2 3 4
Number of function evaluations
x1e4
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(a)
0 1 2 3 4
Number of function evaluations
x1e4
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(b)
0 1 2 3 4
Number of function evaluations
x1e4
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(c)
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Number of function evaluations
x1e4
-900
-800
-700
-600
-500
-400
-300
-200
-100
0
Best function value
GA
GPSA sample 1
GPSA sample 2
(d)
0 1 2 3 4
Number of function evaluations
x1e4
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(e)
0 1 2 3 4
Number of function evaluations
x1e4
10
-17
10
-16
10
-15
10
-14
10
-13
10
-12
10
-11
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(f)
0 1 2 3 4
Number of function evaluations
x1e4
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
Best function value
GA
GPSA sample 1
GPSA sample 2
(g)
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Number of function evaluations
x1e4
-200
-150
-100
-50
0
Best function value
GA
GPSA sample 1
GPSA sample 2
(h)
Figure 10: The comparisons of the performance between GPSA and GA. The results of GPSA were selected through 100
independent trials as the best case and the worst case, and the result of GA was averaged over 100 independent trials. (a)-(h)
correspond to the results of test functions f
1
-f
8
, respectively.
DIGITAL PATTERN SEARCH AND ITS HYBRIDIZATION WITH GENETIC ALGORITHMS FOR GLOBAL
OPTIMIZATION
387