AUTOMATIC VISION-BASED MONITORING OF THE

SPACECRAFT ATV RENDEZVOUS / SEPARATIONS WITH THE

INTERNATIONAL SPACE STATION

A. A. Boguslavsky, V. V. Sazonov, S. M. Sokolov

Keldysh Institute for Applied Mathematics, Miusskaya Sq., 4, Moscow, Russia

A. I. Smirnov, K. U. Saigiraev

RSC ENERGIA, Korolev, Russia

Keywords: Algorithms of determining the motion parameters, space rendezvous / separations processes, accuracy, real

time vision system.

Abstract: The system which allows automating the visual monitoring of the spacecraft ATV rendezvous / separations

with the international space station is being considered. The initial data for this complex is the video signal

received from the TV-camera, mounted on the station board. The offered algorithms of this video signal

processing in real time allow restoring the basic characteristics of the spacecraft motion with respect to the

international space station. The results of the experiments with the described software and real and virtual

video data about the docking approach of the spacecraft with the International Space Station are being

presented. The accuracy of the estimation of the motion characteristics and perspectives of the use of the

package are being discussed.

1 INTRODUCTION

One of the most difficult and crucial stages in

managing the flights of space vehicles is the process

of their docking approach. The price of a failure at

performing of this process is extremely high. The

safety of crew, station and space vehicles also in

many respects depends on a success of its

performance.

The radio engineering means of the docking

approach, which within many years have been used

at docking of the Russian space vehicles, are very

expensive and do not allow to supply docking to not

cooperated station.

As reserve methods of docking approach

monitoring the manual methods are applied, for

which in quality viewfinders the optical and

television means are used. For docking approach of

the pilotless cargo transport vehicle “Progress” to

the orbital station “Mir” a teleoperation mode of

manual control (TORU) was repeatedly used, at

which the realization the crew of the station, having

received the TV image of the station target from a

spacecraft, carried out the manual docking approach.

At the center of the flight management the

control of objects relative motion parameters (range,

speed, angular deviations) should also be carried out.

The semi-automatic TV methods of the monitoring

which are being used till now, do not satisfy the

modern requirements anymore. Recently appeared

means of both the methods of the visual data

acquisition and processing provide an opportunity of

the successful task decision of a complete automatic

determination and control of space vehicles relative

motion parameters.

Flights of the ATV have not begun yet.

Therefore images of the ATV in ground-based

conditions and simulated space images are available

now. But already there are some papers discussing

possible approaches to the decision of similar

images analysis problems (Chi-Chang, H.J. and

McClamroch, N.H., 1993; Casonato, G. and

Palmerini, G.B., 2004). The described approach is

based on experiments with similar system for the

“Progress” spaceship (Boguslavsky et al., 2004).

284

A. Boguslavsky A., V. Sazonov V., M. Sokolov S., I. Smirnov A. and U. Saigiraev K. (2007).

AUTOMATIC VISION-BASED MONITORING OF THE SPACECRAFT ATV RENDEZVOUS / SEPARATIONS WITH THE INTERNATIONAL SPACE

STATION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 284-291

DOI: 10.5220/0001649902840291

Copyright

c

 SciTePress

The system for ATV has a number of differences

from the system used for “Progress”. First of all, this

various arrangement of the TV-camera and special

target for the monitoring of rendezvous / separations

processes. In the ATV case the TV-camera settles

down on ISS, and by the transport vehicle the

special targets (basic and reserve) are established.

Besides that is very important for visual system, the

images of objects for tracking in a field of view have

changed.

In view of operation experience on system

Progress - ISS, in system ATV - ISS essential

changes to the interface of the control panel (see

Part 4) were made.

The main stages of the visual data acquisition

and processing in the complex are realized mostly in

the same way as the actions performed by an

operator.

In the presented field of vision:

1. An object of observation is marked out

(depending on the range of observation, it can be the

vehicle as a whole or a docking assembly or a

special target);

2. Specific features of an object under

observation defined the patterns of which are well

recognizable in the picture (measuring subsystem).

3. Based on the data received:

The position of these elements relative to the

image coordinate system is defined;

Parameters characterizing the vehicle and station

relative position and motion are calculated

(calculation subsystem).

In addition to operator actions, the complex

calculates and displays the parameters characterizing

the approach/departure process in a suitable for

analysis form.

This research work was partially financed by the

grants of the RFBR ## 05-01-00885, 06-08-01151.

2 MEASURING SUBSYSTEM

The purpose of this subsystem is the extraction of

the objects of interest from the images and

performance of measurements of the points’

coordinates and sizes of these objects. To achieve

this purpose it is necessary to solve four tasks:

1) Extraction of the region of interest (ROI)

position on the current image.

2) Preprocessing of the visual data inside the

ROI.

3) Extraction (recognition) of the objects of

interest.

4) Performing the measurements of the sizes and

coordinates of the recognized objects.

All the listed above operations should be

performed in real time. The real time scale is

determined by the television signal frame rate. The

other significant requirement is that in the

considered software complex it is necessary to

perform updating of the spacecraft motion

parameters with a frequency of no less than 1 time

per second.

For reliability growth of the objects of interest

the extraction from the images of the following

features are provided:

- Automatic adjustments of the brightness and

contrast of the received images for the optimal

objects of interest recognition.

- Use of the objects of interest features of the

several types. Such features duplication (or even

triplication) raises reliability of the image processing

when not all features are well visible (in the task 3).

- Self-checking of the image processing results

on a basis of the a priori information about the

observed scenes structure (in the tasks 1-4).

The ways of performing the calculation of the

ROI position on the current image are (the task 1):

1a) Calculation of the ROI coordinates (figure 1)

on the basis of the external information (for

example, with taking into account a scene structure

or by the operator selection).

1b) Calculation of the ROI coordinates and sizes

on the basis of the information received from the

previous images processing.

a)

b)

Figure 1: An example of identification of a region of

interest in the TV camera field of view (1.а) way): а) –

total field of view, b) – a region of interest.

AUTOMATIC VISION-BASED MONITORING OF THE SPACECRAFT ATV RENDEZVOUS / SEPARATIONS

WITH THE INTERNATIONAL SPACE STATION

285

The second (preprocessing) task is solved on the

basis of the histogram analysis. This histogram

describes a brightness distribution inside the ROI.

The brightness histogram should allow the reliable

transition to the binary image. In the considered task

the brightness histogram is approximately bimodal.

The desired histogram shape is provided by the

automatic brightness and contrast control of the

image source device.

Figure 2: Coarse allocation of a target from all candidates

on a basis of the a priory information: the relative sizes of

labels and target plate and their relative location.

At the third processing stage (the task 3) the

extraction of the objects of interest is performed.

These objects are the spaceship contour, the docking

unit disk, the target cross and the target disk with

small labels. The main features are the spaceship

contour, the cross and the target labels. These

features are considered the main structured elements

of the recognized scene and used for measurement.

At features extraction both edge-based (Canny,

1986; Mikolajczyk et al., 2003) and region-based

methods are used (Sonka and Hlavac, 1999).

With accordance to such elements set the

processing of the current field image is being

performed. For example, on distances less than 15

meters are made detection of a target plate, its labels

and a cross. During such processing (figures 1, 2, 3)

the results of the previous measurements can be used

for estimation of the small area of interest position

(figure 1, below). If the previous results are not

present (for example, immediately after system

start), as area of interest is processed the full field

image. During processing among candidates for a

target image of a target it selects the most probable

candidate (figure 2). For its verification the detection

of labels and of radius of a target (figure 3) is

performed. After that the detection of a cross of a

target is performed.

a) b) c)

Figure 3: An example of allocation of an image of a target

on the basis of the coarse coordinates of a target plate and

a priory of the information on an arrangement of labels of

a target. а) - definition of area of interest on a basis a

priory of the information and found coarse location of the

plate; b) area of interest for search of labels of a target; c) -

result of allocation of labels of a target.

Figure 4: An example of allocation of edge of target boxes

and external contour of spaceship (for distance >10

meters). Top-down: extracted edges of the left and the

right boxes; contour of the spaceship; results of the frame

processing (with the marked docking unit image centre).

On distances more than 15 m a label and a cross

of a target reliably are not visible. Therefore the

detection of an external contour of the ship and a

target boxes (figure 4) is realized. Boxes of a target

allow to confirm a hypothesis about the detection of

the ship and to specify its roll position.

The fourth operation (performing of the

measurement) is very straightforward. But for this

operation it is necessary to recognize the reliable

objects results from the previous processing stages.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

286

3 CALCULATION PART

Preprocessing of a frame (more exactly, a half-

frame) gives the following information:

T

– reference time of a frame (in seconds);

CC

YX ,

– real values coordinates of the center of

the cross on the target;

1

N

–number of couples of

points on the horizontal crossbar of the cross;

),,2,1(,

1

NiYX

ii

…=

– integer coordinates of

points on the top of the horizontal crossbar of the

cross;

),,2,1(,

1

NiYX

ii

…=

′

– coordinates of points

on the bottom of the horizontal crossbar of the cross;

2

N

– number of couples of points on the vertical

crossbar of the cross;

),,2,1(,

2

NiVU

ii

…=

–

coordinates of points on the left side of vertical

crossbar of the cross;

),,2,1(,

2

NiVU

ii

…=

′

–

coordinates of points on the right side of vertical

crossbar of the cross;

RYX

OO

,,

– coordinates of

the center of the circle on the target and its radius;

),,2,1(,,

33

NiBAN

ii

…=

– number of points on

the circle and their coordinates;

SSS

RYX ,,

–

coordinates of the center of the circle, which is the

station outline, and its radius (real numbers).

Here all coordinates are expressed in pixels.

Successful preprocessing a frame always gives the

values of

CC

YX ,

and

RYX

OO

,,

, but if there is an

opportunity, when appropriate

0>

k

N

, those

quantities are determined once again by original

information. Bellow we describe the calculation of

those quantities in the case when

0,0,0

321

>>> NNN

and

0=

S

R

. If

S

R

differs

from zero, the data are used in other way (see

bellow).

Determining the coordinates of the cross center.

We change the data

i

ii

Y

YY

→

′

+

2

,

i

ii

U

UU

→

′

+

2

),2,1( …=i

and get coordinates of two sequences of points,

which lie in centerlines of horizontal and vertical

crossbars of the cross. Those centerlines have

equations

1

cyax =−

(horizontal) and

2

cayx

=

+

(vertical). Here

a

,

1

c

and

2

c

are coefficients. The

form of the equations takes into account the

orthogonality of these lines. The coefficients are

determined by minimization of the quadratic form

∑∑

==

+++−−

21

1

2

1

2

1

)()(

N

j

jj

N

i

ii

caVUcYXa

on

21

,, cca

, i.e. by solving the linear least squares

problem. The coordinates of the cross center are

2

21

*

1 a

cac

X

C

+

=

,

2

21

*

1 a

acc

Y

C

+

−

=

.

Determining the radius and the center of the

target circle is realized in two stages. In the first

stage, we obtain preliminary estimations of these

quantities based on elementary geometry. In the

second stage, we solve the least squares problem

minimizing the expression

()()

∑

=

⎥

⎦

⎤

⎢

⎣

⎡

−−+−=Φ

3

1

2

22

2

N

i

OiOi

RYBXA

on

RYX

OO

,,

by Gauss-Newton method (Bard,

1974). Let its solution be

***

,, RYX

OO

. As a rule,

||

*

OO

XX −

and

||

*

OO

YY −

do not exceed 1.5

pixels. Below for simplicity of notations, we will not

use an asterisk in designations of recomputed

parameters.

3.1 Basic Geometrical Ratios

We use the right Cartesian coordinate system

321

yyCy

, which is connected with the target. The

point

C

is the center of the target circle, the axis

3

Cy

is directed perpendicularly to the circle plane

away from station, i.e. is parallel a longitudinal axis

of the Service module, the axis

+

2

Cy

intersects a

longitudinal axis of the docking device on the

Service Module. Also, we use right Cartesian

coordinate system

321

xxSx

connected with the TV

camera on the spacecraft. The plane

21

xSx

is an

image plane of the camera, the axis

3

Sx

is a camera

optical axis and directed on movement of the

spacecraft, the axis

−

2

Sx

intersects an axis of the

docking device of the spacecraft. Let

3

1,

||||

=ji

ij

a

be the

transition matrix from the system

321

xxSx

to the

system

321

yyCy

. The transition formulas are

)3,2,1(

3

1

=+=

∑

=

ixady

j

jijii

,

∑

=−= )3,2,1()( jadyx

ijiij

.

Here

321

,, ddd

are coordinates of the point S

in the system

321

yyCy

.

AUTOMATIC VISION-BASED MONITORING OF THE SPACECRAFT ATV RENDEZVOUS / SEPARATIONS

WITH THE INTERNATIONAL SPACE STATION

287

The matrix characterizes ideal docking

)1,1,1(diag|||| −−=

ij

a

. In actual docking the transition

matrix is

1

||||

12

13

23

−−

−

=

ϕϕ

ij

a

where

32

,,

ϕ

are components of the vector of an

infinitesimal rotation of the system

321

xxSx

with

respect to its attitude in ideal docking. We suppose

deviations from ideal docking are small.

If any point has in the system

321

xxSx

the

coordinates

),,(

321

xxx

, its image has in the image

plane the coordinates

3

1

x

fx

=

ξ

,

3

2

x

fx

=

ξ

.

Here

f

is focal length of the camera. The

coordinates

1

ξ

and

2

ξ

, expressed in pixels, were

meant in the above description of processing a single

video frame. Let coordinates of the same point in the

system

321

yyCy

be

),,(

321

yyy

. Then

333323221311

333222111

)()()(

adyadyady

f

iii

i

−+−+−

=

ξ

.

The coordinates of the center of the target circle

the

C in the system

321

yyCy

are

)0,0,0(

, therefore

31221

23321

ddd

fX

O

−+

+−

=

ϕϕ

,

31221

13231

ddd

fY

O

−+

++

−=

ϕϕ

.

In docking

31

|| dd <<

,

32

|| dd <<

, so it is

possible to use the simplified expressions

2

3

1

ϕ

f

d

fd

X

O

−−=

,

1

3

2

ϕ

f

d

fd

Y

O

+=

.

The center of the cross in the system

321

yyCy

has the coordinates

),0,0( b

. In this case under the

similar simplification, we have

2

3

1

ϕ

f

bd

fd

X

C

−

−=

,

1

3

2

ϕ

f

bd

fd

Y

C

+

−

= .

So

)

3

(

3

1

bdd

bdf

O

X

C

X

−

−=−

,

)

3

(

3

2

bdd

bdf

O

Y

C

Y

−

=−

.

The radius

r

of the target circle and radius R of

its image in the image plane are connected by the

ratio

3

/ dfrR =

.

The last three ratios allow to express

3

d

,

1

d

and

2

d

through R ,

OC

XX −

and

OC

YY −

. Then it is

possible to find

1

ϕ

and

2

ϕ

, having solved

concerning these angles the expressions for

OO

YX ,

or

CC

YX ,

. As to the angle

3

ϕ

, the approximate

ratio

a=

3

ϕ

takes place within the framework of

our consideration.

The processing a frame is considered to be

successful, if the quantities

ii

d

ϕ

,

)3,2,1( =i

were

estimated. As a result of successful processing a

sequence of frames, it is possible to determine

spacecraft motion with respect to the station. The

successfully processed frames are used only for

motion determination.

3.2 Algorithm for Determination of the

Spacecraft Motion

The spacecraft motion is determined in real time as a

result of step-by-step processing of a sequence of

TV images of the target. The data are processed by

separate portions.

In each portion is processed in two stages. The

first stage consists in determining the motion of the

spacecraft center of mass; the second stage consists

in determining the spacecraft attitude motion.

Mathematical model of motion is expressed by

formulas

tzzd

211

+

=

,

tzzd

432

+

=

,

tzzd

653

+=

,

tvv

211

+

=

ϕ

,

tvv

432

+

=

ϕ

,

tvv

653

+=

ϕ

.

Here

t

is time counted off the beginning of

processing the frame sequence,

i

z

and

j

v are

constant coefficients. The ratios written out have the

obvious kinematical sense. We denote the values of

the model coefficients, obtained by processing the

portion of the data with number

n

, by

)(n

i

z

,

)(n

j

v

and the functions

)(td

i

,

)(t

i

ϕ

, corresponding to

those coefficients, by

)(

tD

n

i

,

)(

t

n

i

Φ

.

Determining the motion consists in follows. Let

there be a sequence of successfully processed

frames, which correspond to the instants

...

321

<

ttt

. The frame with number k

corresponds to the instant

k

t

. Values of the

quantities

C

X

,

C

Y

, a ,

O

X

,

O

Y

, R , which were

found by processing this frame, are

)(k

C

X

,

)(k

C

Y

, etc.

These values with indexes

1

,,2,1 Kk …=

form the

first data portion, the value with indexes

211

,,2,1 KKKk …

+

=

– the second one, with

indexes

nnn

KKKk ,,2,1

11

…++=

−−

– the n -th

portion.

The first data portion is processed by a usual

method of the least squares. The first stage consists

in minimization of the functional

∑

=

=Ψ

1

)(

K

k

Az

,

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

288

+

⎥

⎦

⎤

⎢

⎣

⎡

−

+−=

2

)(

3

)(

3

)(

1

)()(

1

][ bdd

bdf

XXwA

kk

k

O

k

C

k

+

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

2

)(

3

)(

3

)(

2

)()(

2

][ bdd

bdf

YYw

kk

k

O

k

C

2

)(

3

)(

3

⎥

⎦

⎤

⎢

⎣

⎡

−

k

d

fr

Rw

Here

)(

ki

k

i

tdd =

,

T

zzzz ),,,(

621

…=

is a

vector of the coefficients, which specify the

functions

)(td

i

,

i

w

, is positive numbers (weights).

The minimization is carried out by Gauss -Newton

method (Bard, 1974). The estimation

)1(

z

of

z

and

the covariance matrix

1

P

of this estimation are

defined by the formulas

[]

)(minarg,,,

1

)1(

6

)1(

2

)1(

1

)1(

zzzzz

T

Ψ== …

,

1

2

1

−

= BP

σ

,

[

]

63

1

)1(

1

2

−

Ψ

=

K

z

σ

.

Here

1

B

is the matrix of the system of the

normal equations arising at minimization of

1

Ψ

. The

matrix is calculated at the point

)1(

z

.

At the second stage, the quantities

⎥

⎦

⎤

⎢

⎣

⎡

−=

)(

1

)1(

3

)1(

2

)()(

1

k

O

k

tD

tfD

Y

f

α

,

⎥

⎦

⎤

⎢

⎣

⎡

+−=

)(

1

)1(

3

)1(

1

)()(

2

k

O

k

tD

tfD

X

f

α

are calculated and three similar linear regression

problems

k

tvv

21

)(

1

+≈

α

,

k

tvv

43

)(

2

+≈

α

,

k

tvva

65

)(

+≈

),,2,1(

1

Kk …=

are solved using the standard least squares method

(Seber, 1977). We content ourselves with

description of estimating the couple of parameters

21

, vv

. We unite them in the vector

T

vvv ),(

21

=

.

The estimations

)1(

1

v

and

)1(

2

v

provide the minimum

to the quadratic form

[]

2

1

21

)(

1

)(

∑

=

−−=

K

k

tvvvF

α

.

Let

1

Q

be the matrix of this form. Then the

covariance matrix of the vector

T

vvv ],[

)1(

2

)1(

1

)1(

=

is

)2/(][

1

)1(

1

−

KvFQ

.

The second data portion is carried out as follows.

At the first stage, the functional

[][]

∑

+=

+−−=Ψ

2

1

)1(

2

)1(

2

)(

K

Kk

k

T

AzzCzzz

is minimized. Here

12

qBC

=

,

q

is a parameter,

10 ≤≤ q

. The estimation of

z

and its covariance

matrix have the form

)(minarg

2

)2(

zz Ψ=

,

1

2

−

= BP

σ

,

[]

6)(3

12

)2(

2

−−

Ψ

=

KK

z

σ

,

where

2

B

is the matrix of the system of the normal

equations, which arise at minimization of

2

Ψ

,

calculated at the point

)2(

z .

At the second stage, the quantities

)(

1

k

α

and

)(

2

k

α

(see above) are calculated and the estimation

of the coefficients

)2(

j

v are found. The estimation

)2(

v

provides the minimum to the quadratic form

[

]

[

]

+−−

′

=

)1(

1

)1(

2

)( vvQvvqvF

T

[]

2

1

21

)(

1

2

1

∑

+=

−−

K

Kk

k

tvv

α

.

Here

q

′

is a parameter,

10 ≤

′

≤ q

. Let

2

Q

be

the matrix of this form. The covariance matrix of the

estimation

)2(

v is

)2/(][

12

)2(

2

1

2

−−

−

KKvFQ

.

The third and subsequent data portions are

processed analogously to the second one. The

formulas for processing the portion with number

n

are obtained from the formulas for processing the

second portion by replacement of the indexes

expressed the portion number:

11 −→ n , n→2 .

Our choice of

n

C

and

)(z

n

Ψ

means that the

covariance matrix of errors in

OC

XX −

,

OC

YY

−

and

R is equal to ),,(diag

1

3

1

2

1

−−−

www .

It is easy to see that

1−

<

nn

BC

, i.e. the matrix

nn

CB

−

−1

is positive definite. The introduction of

the matrix

n

G

provides diminution of influence of

the estimation

)1( −n

z

on the estimation

)(n

z

.

Unfortunately, the matrix

n

G

is unknown. In such

situation, it is natural to take

1−

=

nn

qBC

. One has

1−

<

nn

BC

if

1

<

q

. The described choice of

n

C

means, that procession of the

n -th data portion takes

into account the data of the previous portions. The

data of the

n

-th portion are taken in processing with

the weight 1, the

)1(

−

n

-th portion is attributed the

weight

q

, the

)2(

−

n

-th portion has the weight

2

q

,

etc.

The results of processing the

n -th data portion

are represented by numbers

)(

n

K

n

i

tD

, )(

)(

n

K

n

i

tΦ

),2,1;3,2,1( …

=

ni

. We calculate also the

quantities

2

3

2

1

ddd ++=

ρ

,

d

t

d

u

ρ

=

,

2

3

2

1

2

arctan

dd

d

+

=

α

,

3

1

arctan

d

=

β

.

AUTOMATIC VISION-BASED MONITORING OF THE SPACECRAFT ATV RENDEZVOUS / SEPARATIONS

WITH THE INTERNATIONAL SPACE STATION

289

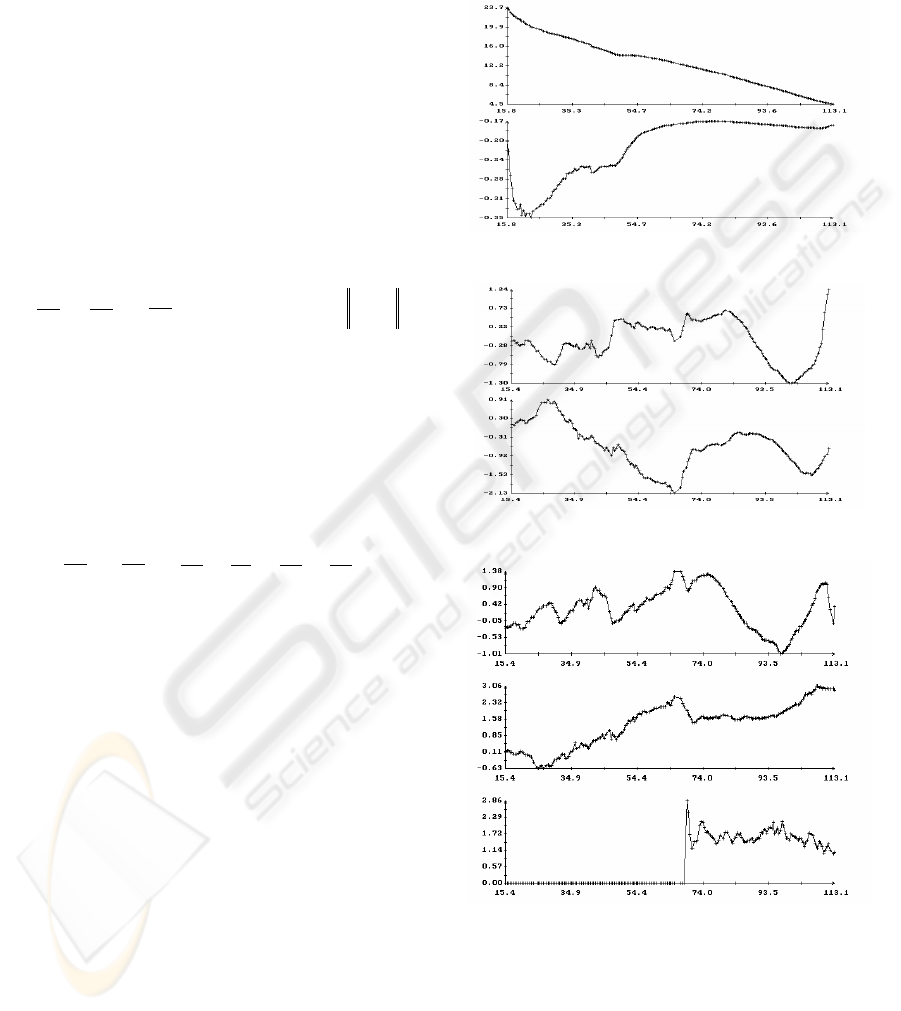
The angle

α

is called a passive pitch angle, the

angle

β

is a passive yaw angle. If docking is close

to ideal (considered case), then

31

|| dd

<

,

32

|| dd <<

and

32

/ dd=

α

,

31

/ dd=

β

.

The angle

1

ϕ

is called an active pitch angle,

2

ϕ

is an active yaw angle,

3

ϕ

is an active roll angle.

We remind these angles have small absolute values.

Characteristics of accuracy of the motion

parameter estimations are calculated within the

framework of the least squares method. For

example, we defined above the covariance matrix

n

P

of the estimation

)(n

z

. In terms of this matrix

the covariance matrix

)(tC

w

of the vector

=

)(tw

()

12

665443221

,,,,,, Rvtvvztzzztzz

T

∈+++ …

is

calculated by formulas

T

nw

z

w

P

z

w

C

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

,

U)U,(U,diag=

∂

z

w

,

00

1 t

U =

.

These formulas concern to the motion which was

found by processing the

n -th of a portion of the

data.

Knowing

)(tC

w

, it is possible to calculate the

standard deviations

)(t

ρ

σ

,

)(t

u

σ

,

)(t

α

σ

and

)(

t

β

σ

of the quantities

)(t

ρ

,

)(tu

,

)(t

α

and

)(t

β

.

The standard deviation

)(t

ρ

σ

has the form

T

w

C

w

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

ρρ

σ

ρ

,

T

d

dd

w

⎟

⎠

⎞

⎜

⎝

⎛

=

∂

ρρρ

ρ

3

21

,0,,0,

.

The similar formulas define the others standard

deviations. The values of

ρ

,

ρ

σ

, u ,

u

σ

, etc.,

referring to the last instant of the processed data

portion, are written on the computer display.

4 EXAMPLES

The experiments with the described complex were

carried out on various samples of the initial data.

The adjustment of system on the images of the

transport ship ATV was carried out on photos of a

breadboard model of the ship in a hangar and on

rendered samples of the 3D ship model trajectories.

Other initial data were real video received from a

board of the ship "Progress". These data were used

for an estimation of reliability and correctness of the

detection of real objects, and also for the verification

of algorithms of relative movement parameters

calculation.

Figures 5, 6 give examples of the operation of

the described algorithm estimating the spacecraft

motion. Figure 5 contains the plots of the functions

)(t

ρ

,

)(tu

,

)(t

α

and

)(t

β

and

)(t

i

ϕ

)3,2,1( =i

.

On

)(t

ρ

and

)(tu

plots the scale on a vertical axis

differs on 2 order.

ρ

(m), u (m/s)

t (s)

β

α

,

(deg.)

t (s)

321

,,

ϕϕϕ

(deg.)

t (s)

Figure 5: Results of the determination of the spacecraft

motion in docking approach.

Figure 6 presents the plots of the standard

deviations

)(t

ρ

σ

,

)(t

u

σ

,

)(t

α

σ

,

)(t

β

σ

. The values

of all these functions were calculated at the last

instants of processed data portions. These values

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

290

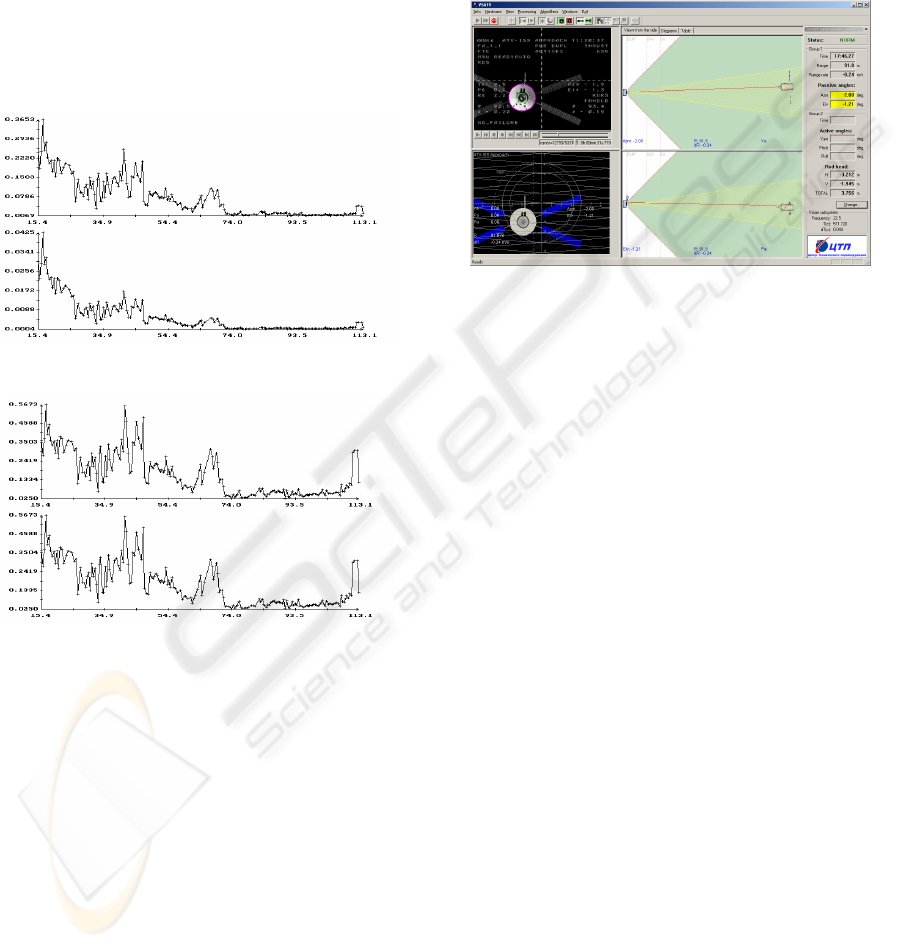
were shown by marks. Each portion contained 10

instants with measurements:

10

1

=−

−nn

KK

. For

clearness, the markers were connected by segments

of straight lines, therefore presented plots are broken

lines. Only the vertexes of these broken lines are

significant. Their links are only interpolation, which

is used for visualization and not always exact. As it

is shown in figure 6, the spacecraft motion on the

final stage of docking was defined rather accurately.

Figure 7 shows an example of the basic screen of

the main program of a complex.

ρ

σ

(m),

u

σ

(m/s)

t (s)

βα

σ

, (deg.)

t (s)

Figure 6: Accuracy estimations for the motion presented

on Figure 5.

5 CONCLUSION

The described complex is being prepared for the use

as a means allowing the ground operators to receive

the information on the motion parameters of the

spacecraft docking to ISS in real time.

The most essential part of this information is

transferred to the Earth (and was always transferred)

on the telemetering channel. It is also displayed on

the monitor. However this so-called regular

information concerns the current moment and

without an additional processing can’t give a

complete picture of the process. Such an additional

processing is much more complicated than the

organizational point of view and more expensive

than processing the video image. It is necessary to

note, that the estimation of kinematical parameters

of the moving objects on the video signal, becomes

now the most accessible and universal instrument of

solving such kind of problems in situations, when

the price of a failure is rather insignificant.

Figure 7: Main screen of the VSATV program.

REFERENCES

Boguslavsky A.A., Sazonov V.V., Smirnov A.I., Sokolov

S.M., Saigiraev K.S., 2004. Automatic Vision-based

Monitoring of the Spacecraft Docking Approach with

the International Space Station. In Proc. of the First

International Conference on Informatics in Control,

Automation and Robotics (ICINCO 2004), Setúbal,

Portugal, August 25-28, 2004, Vol. 2, p.79-86.

Chi-Chang, H.J., McClamroch, N.H., 1993. Automatic

spacecraft docking using computer vision-based

guidance and control techniques. In Journal of

Guidance, Control, and Dynamics, vol.16, no.2:

pp. 281-288.

Casonato, G., Palmerini, G.B., 2004. Visual techniques

applied to the ATV/ISS rendezvous monitoring. In

Proc. of the IEEE Aerospace Conference, vol. 1,

pp. 619-625.

Canny, J. 1986. A computational approach to edge

detection. In IEEE Trans. Pattern Anal. and Machine

Intelligence, 8(6): pp. 679-698.

Mikolajczyk, K., Zisserman, A., Schmid, C., 2003. Shape

recognition with edge-based features. In Proc. of the

14th British Machine Vision Conference

(BMVC’2003), BMVA Press.

Sonka, M., Hlavac, V., Boyle, R. 1999. Image Processing,

Analysis and Machine Vision. MA: PWS-Kent.

Bard, Y., 1974. Nonlinear parameter estimation.

Academic Press, New York.

Seber, G.A.F., 1977. Linear regression analysis. John

Wiley and Sons, New York.

AUTOMATIC VISION-BASED MONITORING OF THE SPACECRAFT ATV RENDEZVOUS / SEPARATIONS

WITH THE INTERNATIONAL SPACE STATION

291