NEW APPROACH TO GET AUTONOMOUS AND FAST ROBOT

LEARNING PROCESSES

R. Iglesias

, M. Rodr

ıguez

, C.V. Regueiro

, J. Correa

, Pablo Quint

ıa

and S. Barro

Electronics and Computer Science, University of Santiago de Compostela, Spain

Dept. of Electronic and Systems, University of Coru ˜na, Spain

Keywords:

Reinforcement learning, mobile robotics, robot control, autonomous agents, genetic algorithms.

Abstract:

Research on robot techniques that are fast, user-friendly, and require little application-speciﬁc knowledge

by the user, is more and more encouraged in a society where the demand of home-care or domestic-service

robots is increasing continuously. In this context we propose a methodology which is able to achieve fast

convergences towards good robot-control policies, and reduce the random explorations the robot needs to

carry out in order to ﬁnd the solutions. The performance of our approach is due to the mutual inﬂuence

that three different elements exert on each other: reinforcement learning, genetic algorithms, and a dynamic

representation of the environment around the robot.

The performance of our proposal is shown through its application to solve two common tasks in mobile

robotics.

1 INTRODUCTION

Reinforcement learning seems to be a very interest-

ing strategy, since all the robot needs for learning a

behaviour is a reinforcement function which tells the

robot how good or bad it has performed but nothing

about the desired set of actions it should have carried

out.

The maximization of the reinforcement allows the

robot to learn a utility function of states and actions

called Q-function, which reﬂects the consequences of

executing every possible action in each state – we will

assume that the robot interacts with the environment

at discrete time steps and it is able to translate the dif-

ferent situations that it may detect through its sensors

into a ﬁnite number of states, S –. Table 1 shows

one of the many reinforcement learning algorithms

that can be applied to teach a robot: the truncated

temporal differences algorithm, TT D(λ, m) (Cichosz,

1997). Basically the robot begins with an initial set

of random negative Q-values: Q(s, a) ≤ 0, ∀s, a, and

then it performs a stochastical exploration of its envi-

ronment. While the robot is moving around, it keeps

track of the m last executed actions so that their corre-

sponding Q-values will be decreased or increased de-

Table 1: Truncated temporal differences algorithm.

1. Observe the current state, s(t): s[0]=s(t)

2. Select an action a(t) for s(t): a[0]=a(t)

3. Perform action a(t)

4. Observe new state s(t+1) and reinforcement value

r(t)

5. r[0]=r(t), u[0]=max

(s(t + 1), a)

6. For k=0,1,...,m-1 do:

if k=0 then z = r[k] + γu[k]

else z = r[k] + γ(λz + (1 − λ)u[k ]), 0 < γ, λ ≥ 1

7. Update the Q-values:

δ = (z − Q

(s[m − 1], a[m − 1])])

∆Q

(s[m − 1], a[m − 1]) = βδ

pending on whether the robot receives or not negative

reinforcements. The parameters γ, λ, and β (that ap-

pear in table 1), determine how much the Q-values are

changed for every positive or negative reinforcement

the robot receives. As the learning process progresses,

the robot should tend to execute those actions which

seem to be the best ones according to the Q-values,

this is called greedy policy.

Despite the beneﬁts of the RL paradigm in au-

tonomous robot-learning, there are important prob-

292

Iglesias R., Rodríguez M., V. Regueiro C., Correa J., Quintía P. and Barro S. (2007).

NEW APPROACH TO GET AUTONOMOUS AND FAST ROBOT LEARNING PROCESSES.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 292-295

DOI: 10.5220/0001649802920295

 SciTePress

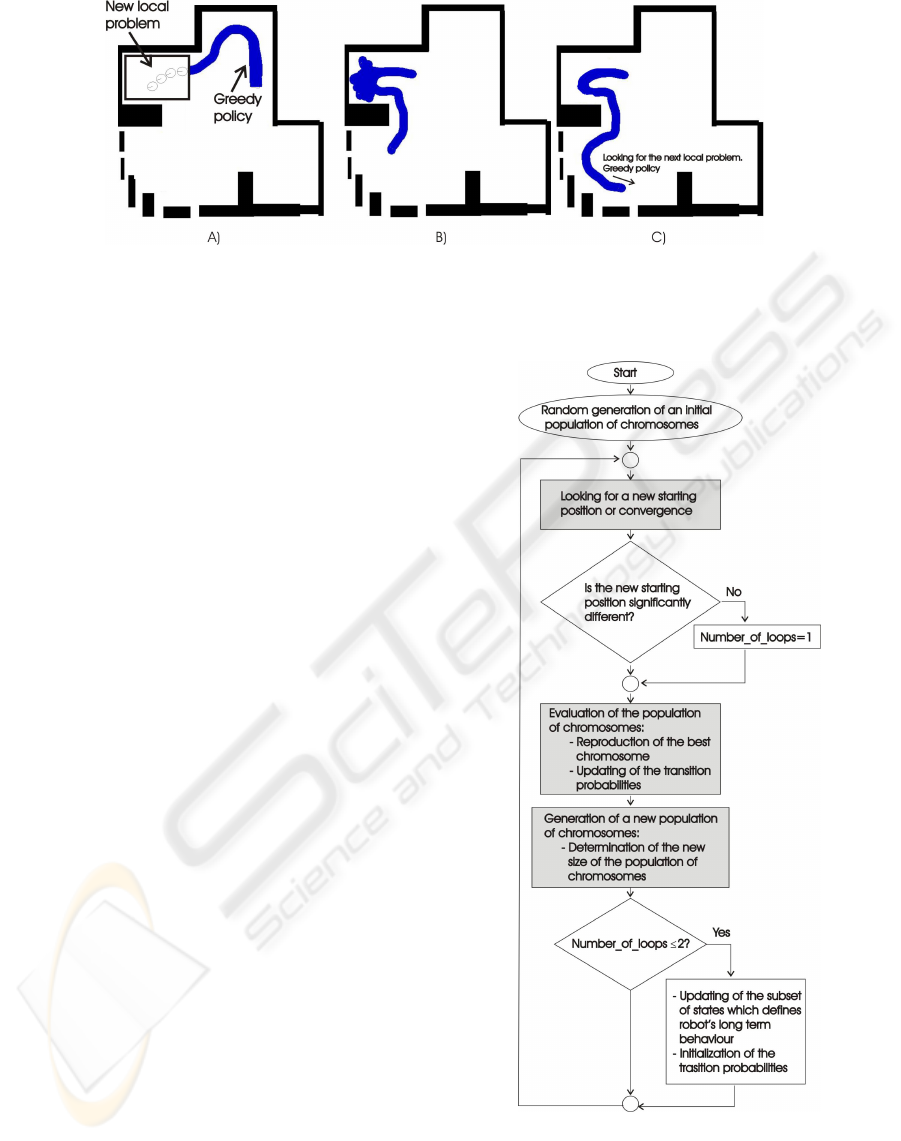
Figure 1: Schematic representation of our approach. Initially the robot moves using the greedy control policy until it ﬁnds a

situation it doesn’t know how to solve (a), a genetic algorithm is applied to ﬁnd a solution (b), once the problem is solved the

greedy policy is applied again (c).

lems to consider when it is applied. First, the time

required to learn a good greedy policy increases expo-

nentially with the number of states and the number of

actions that are possible to execute in each state. On

the other hand, the robot wastes an enormous amount

of time trying actions that are clearly inappropriate

for the task but that are selected randomly during the

learning process.

2 OUR APPROACH

To solve part of the drawbacks just mentioned, we

propose a learning strategy which combines three el-

ements: reinforcement learning (RL), a genetic algo-

rithm (GA), and a dynamic representation of the en-

vironment around the robot (states). Basically, when

our approach is applied the robot goes through three

cyclical and clearly differentiated stages –ﬁgure 2–:

a) looking for a new starting position or convergence.

b) exploration, and c) generation of a new population

of solutions (chromosomes) for the next exploration

stage.

2.1 Looking for a New Starting Position

During this ﬁrst stage the greedy policy is applied to

control the robot. If the robot encounters a situation

where it doesn’t know how to move – local problem,

(ﬁgure 1.a) –, it receives a sequence of consecutive

negative reinforcements, and its position several steps

before the failure is established as a new starting po-

sition for the next exploration stage.

2.2 Exploration Stage

Our strategy applies a GA (Davidor, 1991; Cobb and

Grefenstette, 1993) in order to solve each local prob-

Figure 2: Flow diagram which describes the combination of

RL and GA.

lem the robot ﬁnds. The GA starts with a population

of solutions called chromosomes. Each chromosome

–represented as π– determines the action the robot has

NEW APPROACH TO GET AUTONOMOUS AND FAST ROBOT LEARNING PROCESSES

293

to carry out at each state, s: π(s). The population

of chromosomes is evaluated according to an objec-

tive function called ﬁtness function, which reﬂects for

how long a chromosome is able to properly control

the movement of the robot – ﬁgure 1.b –. Once a

population of chromosomes has been evaluated, the

sequence of states, actions, and rewards the robot re-

ceived under the control of the best chromosome, is

replicated off-line several times to speed up the con-

vergence of the Q-values.

2.3 Generation of a New Population of

Solutions (Chromosomes)

The population of chromosomes has to be evolved

according to the ﬁtness values. In order to do this,

certain genetic operators like mutation –which carries

out random changes in the chromosomes–, or chro-

mosome crossover –which combines chromosomes to

raise new solutions– have to be applied. We use the

Q-values to bias the genetic operators and thus reduce

the number of chromosomes which are required to

ﬁnd a solution. Given a particular chromosome π, the

probability that mutation changes the action that this

chromosome suggests for a particular state s: π(s),

depends on how many actions look better or worse

than π(s) according to the Q-values.

On the other hand, one of the chromosomes

should always be the greedy policy because it brings

together all that has been already learnt by the robot,

and it represents the best chance to have a fast conver-

gence towards the desired solution.

Finally, when the robot is looking for a new start-

ing position and the greedy policy is being used to

control it, if the robot moves properly during M steps

before it receives negative reinforcements, only the

states involved in the last K robot’s movements are

susceptible of being changed through the GA, while

the states involved in the initial M-K actions are la-

belled as learnt, so that neither chromosome selection

nor chromosome crossover can alter them.

The population of chromosomes is resized after

its evaluation according to how close the GA is to the

desired solution.

2.4 Dynamic Representation of States

We use the properties of the regular Markov chains

(Bertsekas and Tsitsiklis, 1996) to reduce the num-

ber of states which are considered during the learn-

ing process. The transition matrix and what is called

steady vector are estimated, so that only those states

with a non-cero entry in the steady vector are con-

sidered in the learning procedure. The steady vector

contains the probability of ﬁnding the robot in each

possible state in the long-term.

3 EXPERIMENTAL RESULTS

We applied our approach to teach a mobile robot two

common tasks: “wall following” and “door traver-

sal”. We have used a Nomad200 robot equipped with

16 ultrasound sensors encircling its upper part and

bumpers. In all the experiments the linear velocity

of the robot was kept constant (15.24 cm/s), and the

robot received the commands it had to execute every

300ms.

We used a set of two layered Kohonen networks to

translate the large number of different situations that

the ultrasound sensors located on the front and right

side of the robot may detect, into a ﬁnite set of 220

neurones – states – (R. Iglesias and Barro, 1998).

3.1 Wall Following

To teach the robot how to follow a wall located on

its right at a certain distance interval, we used a rein-

forcement signal that is negative whenever the robot

goes too far or too close from the wall being followed.

The robot was taught how to perform the task in a sim-

ulated training environment, but its performance was

tested in a different one. Convergence was detected

when the greedy policy was able to properly control

the movement of the robot for an interval of 10 min-

utes.

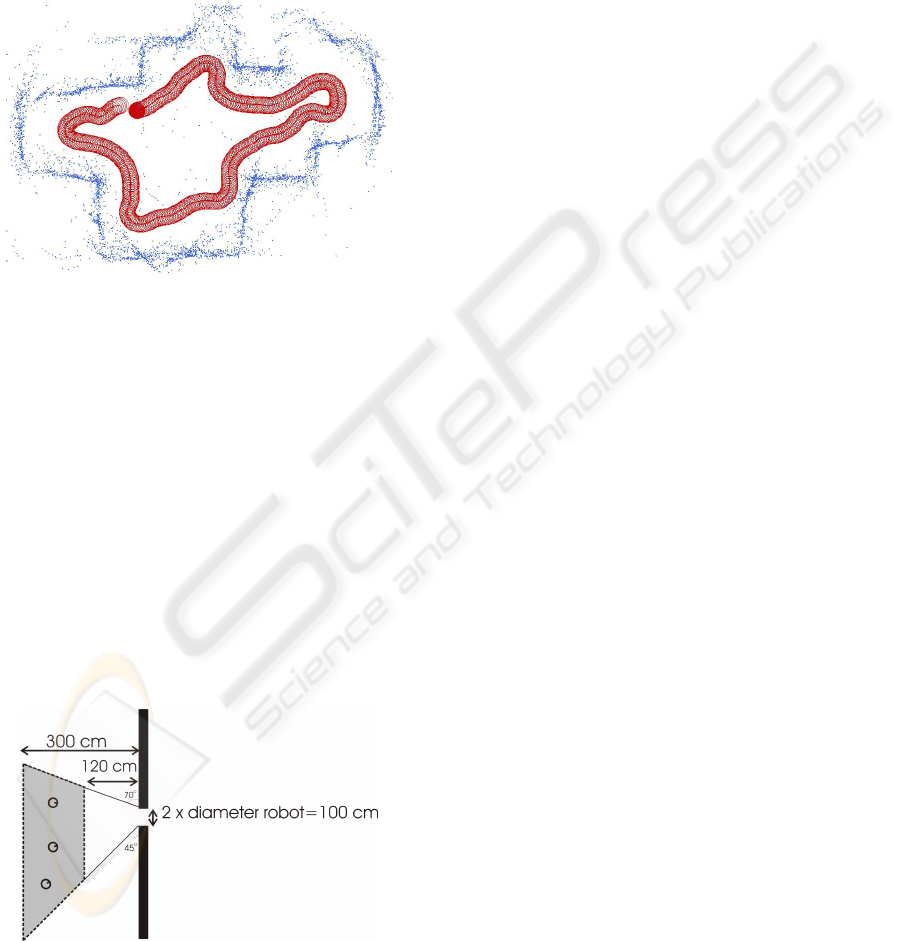
Figure 3: Real robot’s trajectory along a corridor when a

control policy learnt through our approach was used. For

a clear view of the trajectory, ﬁgure a) shows the robot’s

movement in one direction and b) shows the movement

along the opposite direction. Points 1 and 2 in both graphs

correspond to the same robot position. The small dots rep-

resent the ultrasound readings.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

294

When we applied our approach the average re-

quired learning time after 19 experiments was only

25 minutes and 9 seconds –the number of chromo-

somes varied dynamically within the interval [3,20].

When the T T D(λ, m) was applied with the best com-

bination of parameters we found – β = 0.35, λ = 0.8,

γ = 0.95 and m = 30–, the average learning time after

6 experiments was 97 minutes and 30 seconds.

Figure 4: Real robot’s trajectory when the same control pol-

icy as in ﬁgure 3 was used.

To prove that the behaviours learnt through our ap-

proach are useful, ﬁgures 3 and 4 show the movement

of the robot in two real and noisy environments.

3.2 Door Traversal

We also applied our approach to teach a robot how

to cross a door in the experimental scenario shown

in ﬁgure 5. To learn this task the reinforcement is

negative whenever the robot collides with the door-

frame, the robot goes too far from the door, or the

movement direction is so wrong that the robot is not

facing the door any more. After 21 experiments, the

average learning time was 86 minutes and 42 seconds.

Figure 5: Experimental scenario for the door traversal be-

haviour. The initial positions of the robot were within the

shaded area.

4 CONCLUSION

In this article we suggest the use of a new approach

based on the combination of a genetic algorithm and

the reinforcement learning paradigm to teach a robot

how to accomplish different tasks. Our approach is

mainly characterized by three aspects: 1) There are

clearly differentiated exploration stages where the use

of a GA which keeps less information than the RL,

and through which the attention is only focused on

those actions which seem to be proﬁtable, allows the

robot to carry out a fast search of solutions to those

situations where the robot doesn’t know how to move.

2) The information learnt through the reinforcements

– Q-values – is used to bias the genetic operators –

mutation, crossover, selection– and thus improve the

performance of the GA. 3) Finally, the properties of

the regular Markov chains represent a powerful tool

to focus the attention on those states relevant in the

robot’s long term behaviour, avoiding the use of a big

and unnecessary number of states which would delay

the achievement of a good robot-control policy.

ACKNOWLEDGEMENTS

The authors thank the support from grants TIN2005-

03844, PGIDIT04TIC206011PR, TIC2003-09400-

C04-03.

REFERENCES

Bertsekas, D. P. and Tsitsiklis, J. N. (1996). Neuro-Dynamic

Programming. Athena Scientiﬁc.

Cichosz, P. (1997). Reinforcement Learning by Truncating

Temporal Differences. PhD thesis, Dpt. of Electron-

ics and Information Technology, Warsaw University

of Technology.

Cobb, H. G. and Grefenstette, J. J. (1993). Genetic al-

gorithms for tracking changing environments. In

Proc. Fifth International Conference on Genetic Al-

gorithms.

Davidor, Y. (1991). Genetic algorithms and robotics. A

heuristic strategy for optimization. World Scientiﬁc.

R. Iglesias, C. V. Regueiro, J. C. and Barro, S. (1998). Im-

proving wall following behaviour in a mobile robot

using reinforcement learning. In ICSC International

Symposium on Engineering of Intelligent Systems,

EIS’98.

NEW APPROACH TO GET AUTONOMOUS AND FAST ROBOT LEARNING PROCESSES

295