GENETIC REINFORCEMENT LEARNING OF FUZZY
INFERENCE SYSTEM APPLICATION TO MOBILE ROBOTIC
Abdelkrim Nemra, Hacene Rezine and Abdelkrim Souici
Unit of Control, Robotic and Productic Laboratory
Polytechnical Military School
Keywords: Reinforcement learning, Fuzzy controllers’ Genetic algorithm, mobile robotic.
Abstract: An efficient genetic reinforcement learning algorithm for designing Fuzzy Inference System (FIS) with out
any priory knowledge is proposed in this paper. Reinforcement learning using Fuzzy Q-Learning (FQL) is
applied to select the consequent action values of a fuzzy inference system, in this method, the consequent
value is selected from a predefined value set which is kept unchanged during learning and if the optimal
solution is not present in the randomly generated set, then the performance may be poor. Also genetic
algorithms (Genetic Algorithm) are performed to on line search for better consequent and premises
parameters based on the learned Q-values as adaptation function. In Fuzzy-Q-Learning Genetic Algorithm
(FQLGA), memberships (premises) parameters are distributed equidistant and the consequent parts of fuzzy
rules are randomly generated. The algorithm is validated in simulation and experimentation on mobile robot
reactive navigation behaviors.
1 INTRODUCTION
In the last decade, fuzzy logic has supplanted
conventional technologies in some scientific
applications and engineering systems especially in
control systems, particularly the control of the
mobile robots evolving (moving) in completely
unknown environments. Fuzzy logic has the ability
to express the ambiguity of human thinking and
translate expert knowledge into computable
numerical data. Also, for real-time applications, its
relatively low computational complexity makes it a
good candidate. A fuzzy system consists of a set of
fuzzy if-then rules. Conventionally, the selection of
fuzzy if-then rules often relies on a substantial
amount of heuristic observation to express the
knowledge of proper strategies
Recently, many authors proved that it is possible
to reproduce the operation of any standard
continuous controller using fuzzy controller (Jouffe,
1996), (Watkins, 1992), (Glorennec, 1997),
(Dongbing, 2003). However it is difficult for human
experts to examine complex systems, then it isn't
easy to design an optimized fuzzy controller.
Generally the performances of a system of fuzzy
inference (SIF) depend on the formulation of the
rules, but also the numerical specification of all the
linguistic terms used and an important number of
choices is given a priori also it is not always easy or
possible to extract these data using human expert.
These choices are carried with empirical methods,
and then the design of the FIS can prove to be long
and delicate vis-à-vis the important number of
parameters to determine, and can lead then to a
solution with poor performance. To cope with this
difficulty, many researchers have been working to
find learning algorithms for fuzzy system design.
These automatic methods enable to extract
information when the experts’ priori knowledge is
not available.
The most popular approach to design FLC may
be a kind of supervised learning where the training
data is available. However in real applications
extraction of training data is not always easy and
become impossible when the cost to obtain training
data is expensive. For these problems, reinforcement
learning is more suitable than supervised learning. In
reinforcement learning, an agent receives from its
environment a critic, called reinforcement, which
can be thought of as a reward or a punishment. The
objective then is to generate a policy maximizing on
average the sum of the rewards in the course of time,
starting from experiments (state, action, reward).
206
Nemra A., Rezine H. and Souici A. (2007).
GENETIC REINFORCEMENT LEARNING OF FUZZY INFERENCE SYSTEM APPLICATION TO MOBILE ROBOTIC.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 206-213
DOI: 10.5220/0001645902060213
Copyright
c
 SciTePress

This paradigm corresponds to one of the
fundamental objectives of the mobile robotics which
constitutes a privileged applicability of
reinforcement learning. The paradigm suggested is
to regard behaviour as a sensor-effectors
correspondence function. The objective is to favour
the robots autonomy using learning algorithms.
In this article, we used the algorithm of
reinforcement learning, Fuzzy Q-Learning (FQL)
(Jouffe, 1996), (Souici, 2005) which allows the
adaptation of apprentices of the type SIF (continuous
states and actions), fuzzy Q-learning is applied to
select the consequent action values of a fuzzy
inference system. For these methods, the consequent
value is selected from a predefined value set which
is kept unchanged during learning, and if an
improper value set is assigned, and then the
algorithm may fail. Also, the approach suggested
called Fuzzy-Q-Learning Genetic Algorithm
(FQLGA), is a hybrid method of Reinforcement
Genetic combining FQL and genetic algorithms for
on line optimization of the parametric characteristics
of a SIF. In FQLGA we will tune free parameters
(precondition and consequent part) by genetic
algorithms (GAs) which is able to explore the space
of solutions effectively.
This paper is organized as follows. In Section 2,
overviews of Reinforcement learning,
implementation and the limits of the Fuzzy-Q-
Learning algorithm is described. The
implementation and the limits of the Fuzzy-Q-
Learning algorithm are introduced in Section 3.
Section 4 describes the combination of
Reinforcement Learning (RL) and genetic algorithm
(GA) and the architecture of the proposed algorithm
called Fuzzy-Q-Learning Genetic Algorithm
(FQLGA). This new algorithm is applied in the
section 5 for the on line learning of two elementary
behaviors of mobile robot reactive navigation, “Go
to Goal” and “Obstacles Avoidance”. Finally,
conclusions and prospects are drawn in Section 6.
2 REINFORCEMENT LEARNING
As previously mentioned, there are two ways to
learn either you are told what to do in different
situations or you get credit or blame for doing good
respectively bad things. The former is called
supervised learning and the latter is called learning
with a critic, of which reinforcement learning (RL)
is the most prominent representative. The basic idea
of RL is that agents learn behaviour through trial-
and-error, and receive rewards for behaving in such
a way that a goal is fulfilled.
Reinforcement signal, measures the utility of the
exits suggested relative with the task to be achieved,
the received reinforcement is the sanction (positive,
negative or neutral) of behaviour: this signal states
that it should be done without saying how to do it.
The goal of reinforcement learning is to find the
behavior most effective, i.e. to know, in each
possible situation, which action is achieved to
maximize the cumulated future
rewards.Unfortunately the sum of rewards could be
infinite for any policy. To solve this problem a
discount factor is introduced.
k
k
k0
rR
γ
∞
≠
=
∑
(1)
Where 0 ≤ γ ≤ 1 is the discount factor.
The idea of RL can be generalized into a model,
in which there are two components: an agent that
makes decisions and an environment in which the
agent acts. For every time step, the agent perceives
information from the environment about the current
state, s. The information perceived could be, for
example, the positions of a physical agent, to
simplify say the x and y coordinates. In every state,
the agent takes an action u
t
, which transits the agent
to a new state. As mentioned before, when taking
that action the agent receives a reward.
Formally the model can be written as follows;
for every time step t the agent is in a state st
∈
S
where S is the set of all possible states, and in that
state the agent can take an action at
∈ (At), where
(At) is the set of all possible actions in the state st.
As the agent transits to a new state st+1 at time t + 1
it receives a numerical reward rt+1. It up to date
then its estimate of the function of evaluation of the
action using the immediate reinforcement, rt
+1
, and
the estimated value of the following state, Vt (St
+1
),
which is defined by:
(
)()
1
11
max ,
tt
tt t t
uU
Vs Qs u
+
++
∈
= (2)
The Q-value of each state/action pair is updated by:
(
)
(
)()()
{
}
111
,, ,
tt t t t t t t t t
Qs u Qsu r V s Qsu βγ
+++
=++−
(3)
Where
(
)
()
,
11
γ +−
++
rVs Qsu
ttt
tt
the TD error
and β is the learning rate.
GENETIC REINFORCEMENT LEARNING OF FUZZY INFERENCE SYSTEM APPLICATION TO MOBILE
ROBOTIC
207

This algorithm is called Q-Learning. It shows
several interesting characteristics. The estimates of
the function Q, also called the Q-values, are
independent of the policy pursued by the agent. To
calculate the function of evaluation of a state, it is
not necessary to test all the possible actions in this
state but only to take the maximum Q-value in the
new state (eq.4). However, the too fast choice of the
action having the greatest Q-value:
()
1
1
arg max ,
tt
ttt
uU
uQsu
+
+
∈
= (4)
can lead to local minima. To obtain a useful
estimate of Q, it is necessary to sweep and evaluate
the whole of the possible actions for all the states: it
is what one calls the phase of exploration (Jouffe,
1996), (Souici, 2005). In the preceding algorithm,
called TD (0), we use only the state which follows
the robot evolution, Moreover only the running state
is concerned. Sutton (Souici, 2005) extended the
evaluation in all the states, according to their
eligibility traces that memorise the previously
visited state action pairs in our case. Eligibility
traces can be defined in several ways (Jouffe, 1996),
(Watkins, 1992), (Souici, 2005). Accumulating
eligibility is defined by:
()
(
)
()
1
1
sinon
1
es siss
t
t
es
t
es
t
γλ
γλ
+=
−
=
−
⎧
⎪
⎨
⎪
⎩
(5)
The algorithm Q (λ) is a generalization of Q-
Learning which uses the eligibilities truces (Souici,
2005): Q-Learning is then a particular case of Q (λ)
when λ=0.
(
)
(
)
(
)
(
)
{
}
()
,, ,.
111
βγ =++ −
+++
Qs u Qsu r V s Qsu e s
tt tt t ttt
tt
(6)
3 FUZZY Q-LEARNING
ALGORITHM
In mobile robotics, input and output variables given
by the sensors and effectors are seldom discrete, or,
if they are, the number of state is very large.
However reinforcement learning such as we
described it uses a discrete space of states and
actions which must be have reasonable size to
enable the algorithms to converge in an acceptable
time in practice.
The principle of the Fuzzy Q-Learning
algorithm consists in choosing for each rule
R
i
a
conclusion among a whole of actions available for
this rule. Then it implements a process of
competition between actions. With this intention, the
actions corresponding to each rule
R
i
have a quality
i
q
which then determines the probability to choose
the action. The output action (discrete or continues)
is then the result of the inference between various
actions locally elected. The matrix q enables to
implement not only the local policies the rules, but
also to represent the function of evaluation of the
overall t-optimal policy.
For every time step t the agent is in a state st
∈
S
where S is the set of all possible states, and in that
state the agent can take an action at
∈(At), where
(At) is the set of all possible actions in the state st.
As the agent receives a numerical reward rt+1
∈
R at
time t + 1, and it transits to a new state st+1. It then
perceives this state by the means of its activated
degree of its rules. The algorithm FQL uses a Policy
of Exploration/Exploitation (PEE) (Jouffe, 1996),
(Souici, 2005), combining a random exploration part
()
i
U ρ and determinist guided part ()
i
U η .
The steps are summarized as follows:
1. Calculate of the evaluation function:
,)())((()(
11
∑
∈
+
∈
+
∗
=
ti
i
AR
tR
i
t
UU
tt
SUqMaxSQ α
2. Calculate the TD error
() (,)
11 1
rQSQSU
tttt
tt t
εγ
∗
=+ −
++ +

3. Update the matrix of
Q
values
i
i
tt
i
t
i
t
Reqq
T
∀+=
++
,
~
.
11
εβ
4. Election of the action to be applied
() ()(), ,
11 1 1
1
i
US Electionq S UU
UR
tt t t
RA
i
t
i
α =∀∈
∑
++ + +
∈
+
Where Election is defined by:
11
() (() () ())
iiii
Ut UUt
E
lection q ArgMax q U U U ηρ
+∈+
=++
5. Update of the eligibility traces
() ,( )
11
()
1
(), sinon
ii i i i
eU U U
ii
t
tt
eU
t
ii
eU
t
γλ φ
γλ
+=
++
=
+
⎧
⎪
⎨
⎪
⎩
And new calculation of the evaluation function.
(, ) ( )(),
11 1 1 1 1
1
ii
QSU qU S
R
tt t t t t
RA
i
t
i
α =
∑
+
++ ++ +
∈
+
This value will be used to calculate the TD error in
the next step time. However the performances of the
controller are closely dependent on the correct
choice of the discrete actions set, witch is
determined using a priori knowledge about system,
for complex systems like robots, priori knowledge
are not available, then it becomes difficult to
determine a set of correct actions in which figure the
optimal action for each fuzzy rule. To solve this
problem and to improve the performances of the
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
208

reinforcement learning, the genetic algorithms will
explore the broadest space of solutions to find the
solution optimal (Dongbing, 2003), (Chia-Feng,
2005), (Min-Soeng, 2000), (Chia-Feng, 2003)
, and
that without any priori knowledge.
4 GENETIC REINFORCEMENT
ALGORITHM
Genetic Algorithms (GA) are stochastic optimization
algorithms, founded on species evolution
mechanisms (Goldberg, 1994). In GA, a candidate
solution for a specific problem is called an
individual or a chromosome and consists of a linear
list of genes. Each individual represents a point in
the search space and, hence, a possible solution to
the problem. A population consists of a finite
number of individuals. Each individual is decided by
an evaluating mechanism to obtain its fitness value.
Based on this fitness value and undergoing genetic
operators, a new population is generated iteratively,
with each successive population referred to as a
generation.
Genetic Reinforcement Learning enable to
determine the best set of parameters of (antecedents
/ consequences) starting from a random initialization
of these parameters and in each iteration, only one
action is applied on the system to the difference of a
traditional genetic algorithm GA use three basic
operators (the selection, crossover, and mutation) to
manipulate the genetic composition of a population:
• Reproduction: Individuals are copied according to
their fitness values. The individuals with higher
fitness values have more offspring than those with
lower fitness values.
• Crossover: The crossover will happen for two
parents that have high fitness values with the
crossover probability p
c. One point crossover is used
to exchange the genes.
• Mutation: The real value mutation is done by
adding a certain amount of noise (Gaussian
in this
paper) to new individuals to produce the offspring
with the mutation probability pm. For the ith variable
in jth individual, it can be expressed as:
(). (0, )
1
aaiN
t
t
β
σ =+
+
(7)
Where N denote a Gaussian noise, and
() exp( )ii
β
=− for the
th
i generation.
4.1 FQLGA Algorithm
Because of its simplicity, a Takagi-Sugeno Fuzzy
inference system is considered, with triangular
membership function. The structure (partition of its
input space, the determination of the number of IF-
THEN rules) of the SIF is predetermined.
i
j
a is a vector representing the discrete set of K
conclusions generated randomly for the rule
i
R
with which is associated a vector
i
j
q
representing the quality of each action (i= 1 ~N and
j= 1 ~ K).
The principle of the approach is to use a
population of K (SIF) and to treat the output of each
one of them as a possible action to apply on the
system. FQL algorithm exploits local quality
function q witch is associated with each action of a
fuzzy rule (équat.6) whereas FQLGA algorithm uses
as function fitness the sum of local qualities q given
by:
()fInd
j
=
(, )
11
1
N
i
QS SIF q
t
t
j
i
=
∑
++
=
(8)
To reduce the training time, the quality matrix Q
is not initialized after each iteration but undergoes
the same genetic operations as those applied to the
set of the individuals (selection, crossing).
4.2 Optimization of the Consequent
Part of a FIS
A population of K individuals of a predetermined
structure is adopted. The size of an individual is
equal to number N of the FIS’s rules. The
architecture of FQLGA algorithm proposed for the
optimization of the conclusions is represented on the
figure (1).
Figure 1:Representation of the individuals and qualities of
the actions in FQLGA algorithm.
GENETIC REINFORCEMENT LEARNING OF FUZZY INFERENCE SYSTEM APPLICATION TO MOBILE
ROBOTIC
209

4.3 Optimization of the Antecedent
Part of a SIF
To find the best set of premises generated by GA, a
population made up of M SIF is created. Each
individual (FIS) of the population encode the
parameters of the antecedents i.e. the modal points
of the FIS and his performance is evaluated by the
fitness function of Q (global quality).
The conclusion part of each individual SIF
remains fixed and corresponds to the values
determined previously. The coding of the
membership functions of the antecedent part of a
FIS (individual) is done according to the figure (2).
To keep the legibility of the SIF, we impose
constraints during the evolution of the FIS to ensure
the interpretability of the FIS.
Figure 2: Coding of the parameters of the antecedent part.
Input N :
1
1Nn
m
N
m
−+
< …. <
1
-2 Nm
m
<
1
Nm
m
The fitness function used in by genetic
algorithm for the optimization of the antecedent part
is the global quality of the FIS which uses the degree
of activation of the fuzzy rules; this fitness function
is given by the following equation:
(()). ()
() ((), )
(())
iA
i
iA
i
Ri î
RR
ii
R
RR
St q t
find QSt SIF
St
α
α
∈
∈
==
∑
∑
(9)
Figure 3: General architecture of FQLGA algorithm.
4.4 Optimization of the Consequent
and Antecedent Part of FIS
A SIF consists of a set of fuzzy rules each one of it
is made of an antecedent and a consequent part.
Optimize the antecedent and the consequent part of
the fuzzy controller at the same time is a complex
problem which can admit several solutions which
are not acceptable in reality, the great number of
possible solutions makes the algorithm very heavy
and can lead to risks of instability.
FQLGA algorithm proposed in (fig.3) for the
optimization of the premises and the conclusions
allows the total parametric optimization of the FIS in
three stages represented in the flow chart (fig.4).
• At the beginning of the learning process, the
quality matrix is initialized at zero, and then
traditional algorithm FQL evaluates each action
using an exploration policy. This step finishes
when a number of negative reinforcements is
received.
• After the evaluation of the individuals, the genetic
algorithm for the optimization of the consequent
part of the fuzzy rules creates a new better adapted
generation. This stage is repeated until obtaining
convergence of the conclusions or after having
reached a certain number of generations. The
algorithm passes then to the third stage:
• Once the conclusions of the FIS are optimized, the
second genetic algorithm for the optimization of
the antecedent part is carried out to adjust the
positions of the input membership functions of the
controller which are initially equidistant on their
universe of discourse.
Figure 4: Flow chart of FQLGA algorithm.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
210

5 EXPERIMENTAL RESULTS
To verify the performance of FQLGA two
elementary behaviors of reactive navigation of a
mobile robot: "Go to Goal" and "Obstacles
Avoidance" are presented in this section; the
algorithm was
adopted in the experiments for both
simulations (
Saphira simulator) and real robots
(Pioneer II).
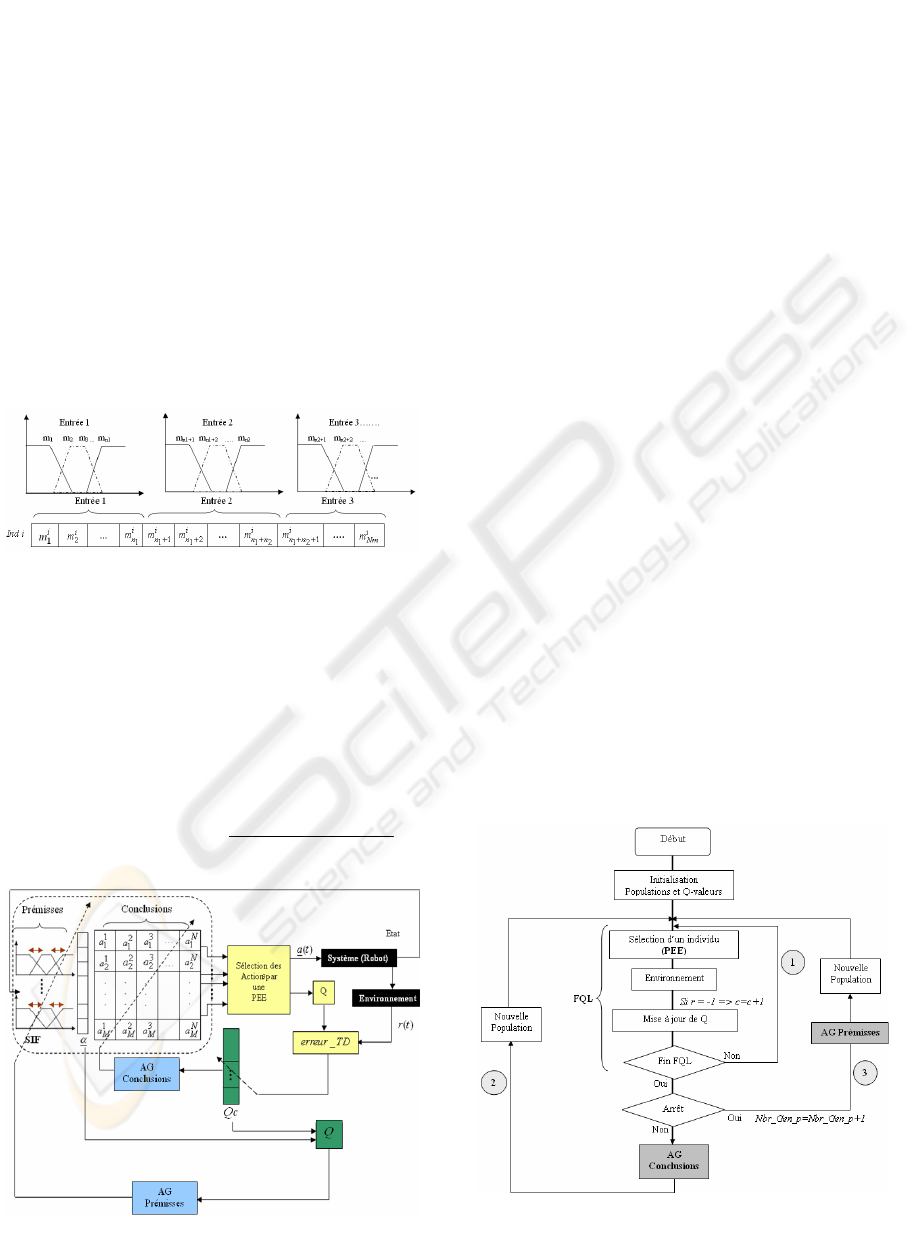
5.1 «Go to Goal» Behaviour
The two input variables are: the angle"
Rb
θ
"
between the robot velocity vector and the robot-goal
vector, and the distance robot-goal "
b
ρ
".They are
respectively defined by three (Negative, Zeros,
Positive) and two (Near, Loin) fuzzy subsets (fig.5).
The two output variables are the rotation speed,
Vrot_CB and the translation speed Vtran_CB each
output is represented by nine actions initialised
randomly.
Figure 5: Membershipfunctions of the input space.
The reinforcement functions adopted for the two
outputs are respectively given by:
_
1 ( 0 -1 1 )
( ) 0 ( 0)
-1
Vrot CB
Si ou
tSi
Else
r
θθ θ
θθ
⋅
<°<<+°
=⋅=
⎧
⎪
⎨
⎪
⎩


(10)
_
10.15 et 800
00
( ) 1 220 et 800 et ( ) 5
0
1
Vtran CB
Si Vtrans
rtSiVtrans abs
Else
ρρ
ρθ
≤≥
=≥≥<
−
⎧
⎪
⎨
⎪
⎩
The parameters of FQL algorithm and the
genetic algorithms are as follows:
LP and Lc respectively indicate the sizes of the
chromosomes for the antecedents and the
conclusions part, Np, Nc respectively represent the
size of the population of the parameters of
antecedent and the conclusions and Pm the
probability of mutation.
The simulation results are given of the first
behaviour "Go to Goal" are presented in the figure
(6), 28 generations were sufficient to find the good
actions.
Figure 6: Go to goal: Training/Validation.
Figure (7) shows the convergence of the fitness
values of the genetic algorithms for the two output
variables Vrot_CB and Vtran_CB obtained during
experimental test.
Figure 7: Fitness functions for the two output variables.
5.2 «Obstacles Avoidance» Behaviour
The Inputs of the FIS are the distances provided by
the ultrasounds sensors to in the three directions
(Frontal, Left and Right) and defined by the three
fuzzy subsets: near (N), means (M), and far (F)
(fig.8).
Figure 8:Memberships Functions of the inputs variables.
The conclusions (rotation speeds) are initialized
randomly. The translation speed of Vtran_EO is
given analytically; it is linearly proportional to the
frontal distance:
max
_
.( _ )
max
V
Vtran EO Dis F Ds
D
=− (11)
maxV is the maximum speed of the robot equal to
350mm/s.
0 20 0 400 600 800 1000 1200 1400 1600 1800 2000
0
0.2
0.4
0.6
0.8
1
Dist ance Frontal e
Degree of mem bership
PM L
0 20 0 400 600 800 1000 1200 1400 1600 1800 2000
0
0.2
0.4
0.6
0.8
1
Distanc e Droite
Degree of mem bership
PM L
0 20 0 400 600 800 1000 1200 1400 1600 1800 2000
0
0.2
0.4
0.6
0.8
1
Distanc e Gauche
Degree of mem bership
PM L
GENETIC REINFORCEMENT LEARNING OF FUZZY INFERENCE SYSTEM APPLICATION TO MOBILE
ROBOTIC
211

0 0. 5 1 1.5 2 2.5 3
x 10
4
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Tem ps
Qual it é du SIF
FQL --- FQLGA
FQL
FQLGA
Optimum Local
maxD is the maximum value measured by the
frontal sensors and estimated to 2000mm and Ds is
a safe distance witch is fixed at 250mm.
The function of reinforcement is defined as
follows (Souici, 2005):
_
1 ( _ ) _ _
_ _ min 800
(12)
()
-1 ( _ ) _ _
__ min800
0
×<
<<
=
×<
<<
Vrot CB
Signe Vrot EO if Dis R Dis L
or Dis F Dis L and D
t
Signe Vrot EO and Dis L Dis R
or Dis F Dis Rand D
elsewhere
r
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
with Dmin=min (Dis_L, Dis_F, Dis_R)
The parameters of FQL algorithm and the
genetic algorithms are identical to the preceding
behaviour except for the sizes of the chromosomes
Lp=12 and Lc=27.
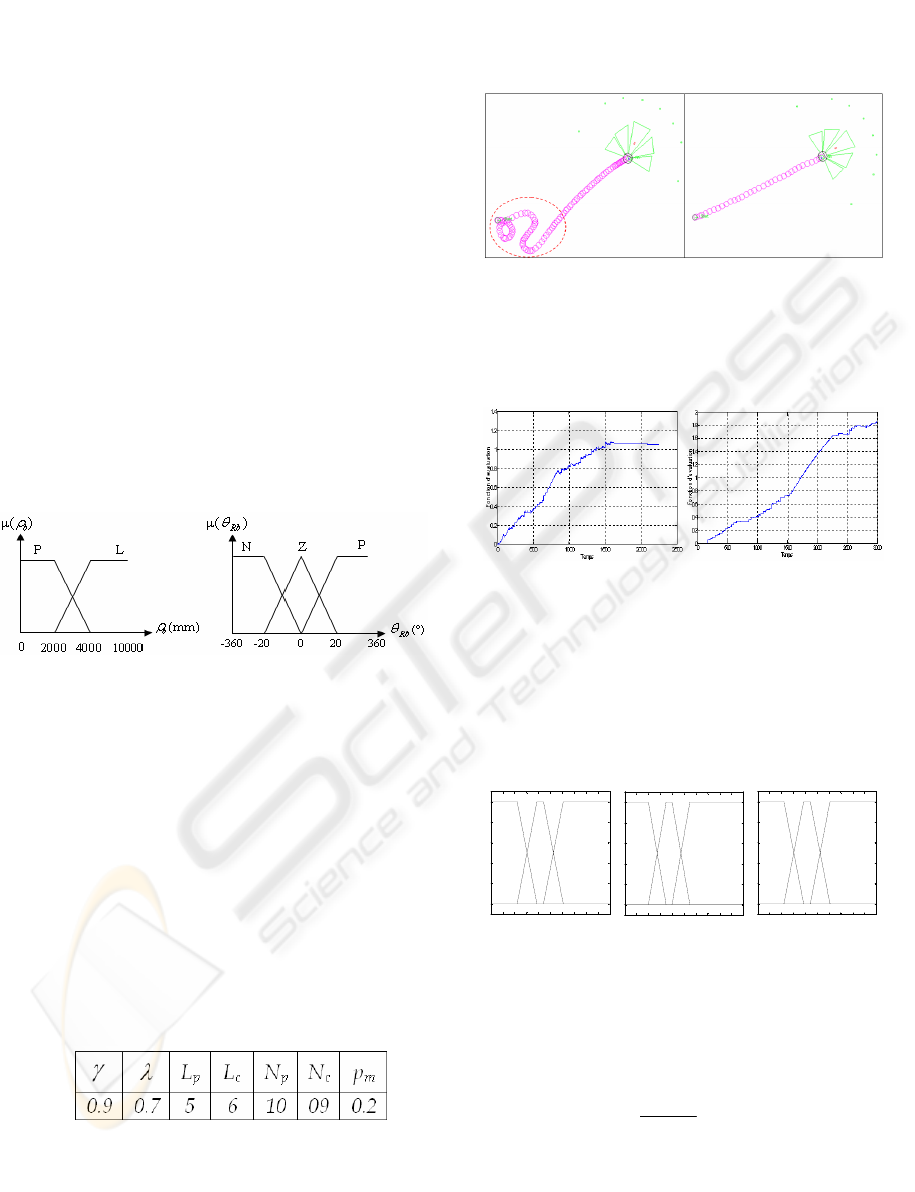
Figure (9) represents the trajectories of the robot
during the learning phase with FQL algorithm and a
random initialization of the consequents part for the
27 fuzzy rules. Several situations of failures are
observed, this example show the limits of traditional
FQL algorithm when priory knowledge about the
system are not available.
Figure 9: Trajectories of the robot obtained by FQL
algorithm using a random initialization of parameters.
The trajectories of figure (10) show the
effectiveness of the association of the reinforcement
learning FQL and the genetic algorithm as stochastic
tool for exploration. FQLGA Algorithm enables to
find an optimal FIS for the desired behaviour
(obstacles avoidance). The duration of learning
depend to the genetic algorithm parameters and the
obstruction density of the environment. We observe
that after each generation the quality of the FIS (sum
of local qualities) increases, which give more chance
to the best individuals to be in the next generations.
Figure 10: Learning/Validation Trajectories of the robot
with FQLGA algorithm for various environments.
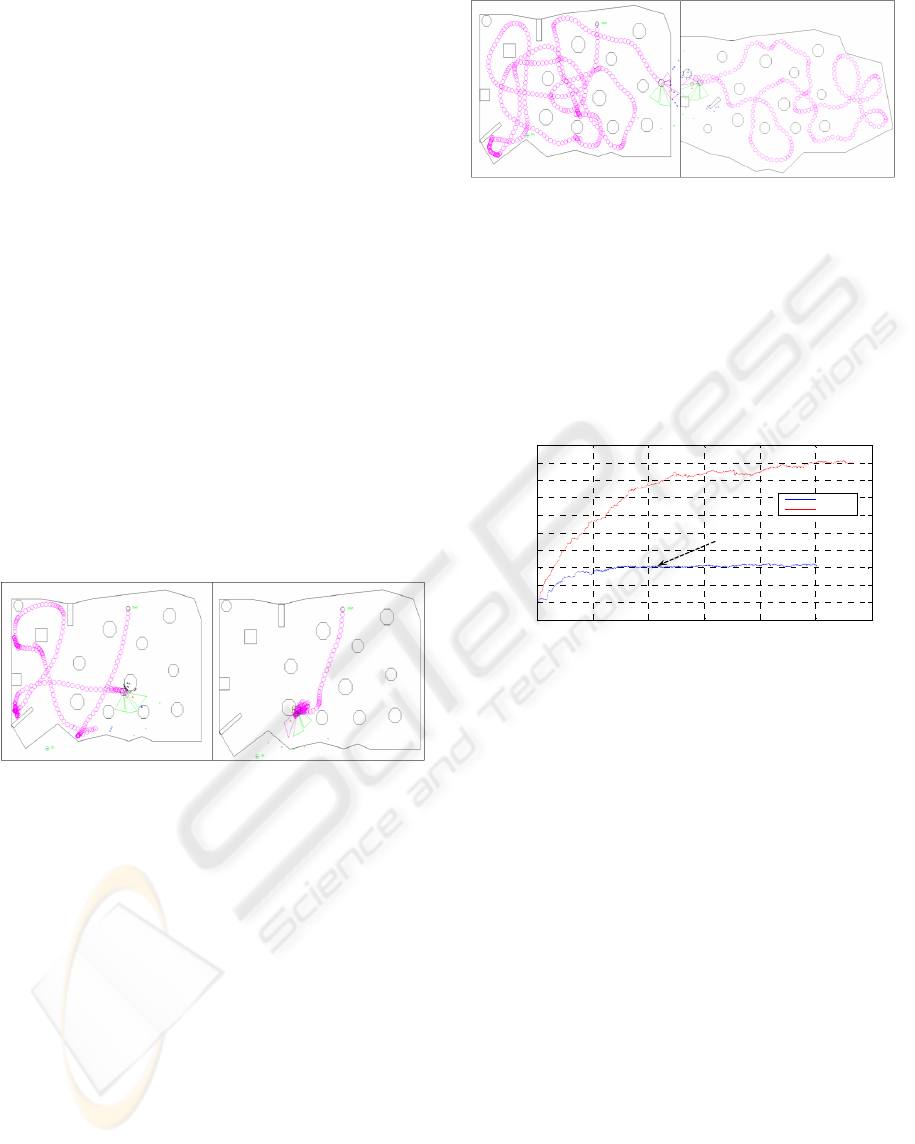
Figure (11) shows the performances of FQLGA
algorithm compared to the FQL algorithm which can
be blocked in a local minimum when the optimal
solution is not present in the randomly generated set
of actions. On the other hand FQLGA algorithm
converges towards the optimal solution
independently of the initialized values.
Figure 11: Evolution of the quality of the Fuzzy controller
with FQL and FQLGA algorithms.
5.3 Experimental Results with the Real
Robot Pioneer II
Figure (12) represents the results of the on line
learning of the robot Pioneer II for the behaviour
"Go to goal". During the learning phase, the robot
does not follow a rectilinear trajectory (represented
in green) between the starting point and the goal
point because several actions are tested
(exploration). Finally the algorithm could find the
good actions, and the robot converges towards the
goal marked in red colour, the necessary time to find
these good actions is estimated at 2mn. Each
generation is generated after having noted twenty
(20) failures. The learning process requires
respectively 32 and 38 generations for GA to
determine rotation and translation speed.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
212

Figure 12: On line learning of the real robot Pioneer II,
"Go to goal" behaviour.
Figure (13) represents the results of the on line
learning of the "Obstacles Avoidance" robot
behaviour. For reasons of safety, we consider that
the minimal distances detected by the frontal sonars
and of left/right are respectively 408 mm and of 345
mm a lower value than these distances is considered
then as a failure and involves a retreat (represented
in green) of the mobile robot. A generation is
created after 50 failures. The genetic algorithms
require 14 generations to optimize the conclusions
and 24 generations to optimize the parameters of the
antecedents. The duration of on line learning is
estimated at 20 min, this time is acceptable vis-à-vis
the heaviness of the traditional genetic algorithms.
Figure 13: On line learning of the real robot Pioneer II,
behaviour "Obstacle Avoidance».
Figure (14) represents the evolution of the fitness
function obtained during this experimentation.
Figure 14: Fitness function evolution, "Obstacles
avoidance" robot behaviour.
6 CONCLUSION
The combination of the reinforcement Q-Learning
algorithm and genetics Algorithms give a new type
of hybrid algorithms (FQLGA) which is more
powerful than traditional learning algorithms.
FQLGA proved its effectiveness when no priori
knowledge about system is available. Indeed,
starting from a random initialization of the
conclusions values and equidistant distribution for
the membership functions for antecedent part the
genetic algorithm enables to find the best individual
for the task indicated using only the received
reinforcement signal. The controller optimized by
FQLGA algorithm was validated on a real robot and
satisfactory results were obtained. The next stage of
this work is the on line optimization of the structure
of the Fuzzy controller.
REFERENCES
L. Jouffe, “Actor-Critic Learning Based on Fuzzy
Inference System”, Proc of the IEEE International
Conference on Systems, Man and Cybernetics.
Beijing, China, pp.339-344, 1996.
C.Watkins, P. Dayan: “Q-Learning Machine Learning”,
pp.279-292, 1992.
P. Y. Glorennec and L. Jouffe, “Fuzzy Q-learning,” Proc.
Of IEEE Int. Con On Fuzzy Systems, pp. 659-662,
1997
Dongbing Gu, Huosheng Hu, Libor Spacek “ Learning
Fuzzy Logic Controller for Reactive Robot
Behaviours” Proc. of IEEE/ASME International
Conference on Advanced Japan, pp.20-24 July, 2003.
A. Souici
: “Apprentissage par Renforcement des
Systèmes d’inférence Floue par des Méthodes par
renforcement application à la navigation réactive d’un
robot mobile
”, Thèse de Magistère, Ecole Militaire
Polytechnique, Janvier 2005.
Chia-Feng Juang “ Combination of online Clustering and
Q-Value Based GA for Reinforcement Fuzzy System
Design” IEEE Transactions On Systems, Man, And
Cybernetics Vol. 13, N°. 3, pp.289-302, June 2005
Min-Soeng Kim and Kim and Ju-Jang Lee. “Constructing
a Fuzzy Logic ControllerUsing Evolutionary Q-
Learning” IEEE. pp.1785-1790, 2000
Chia-Feng Juang and Chun-Feng Lu. Combination of On-
line Clustering and Q-value Based Genetic
Reinforcement Learning For Fuzzy Network Design 0-
7803-7898-9/03/$17.00 0 2003 IEEE.
David Goldberg “Algorithme génétique Exploration,
optimisation et apprentissage automatique”» Edition
Addison-Wesley, France 1994.
GENETIC REINFORCEMENT LEARNING OF FUZZY INFERENCE SYSTEM APPLICATION TO MOBILE
ROBOTIC
213