COMPARING COMBINATIONS OF FEATURE REGIONS FOR

PANORAMIC VSLAM

Arnau Ramisa, Ram

on L

opez de M

antaras

Artiﬁcial Intelligence Research Institute, UAB Campus, 08193, Bellaterra, Spain

David Aldavert, Ricardo Toledo

Computer Vision Center, UAB Campus, 08193, Bellaterra, Spain

Keywords:

Afﬁne covariant regions, local descriptors, interest points, matching, robot navigation, panoramic images.

Abstract:

Invariant (or covariant) image feature region detectors and descriptors are useful in visual robot navigation

because they provide a fast and reliable way to extract relevant and discriminative information from an image

and, at the same time, avoid the problems of changes in illumination or in point of view. Furthermore, com-

plementary types of image features can be used simultaneously to extract even more information. However,

this advantage always entails the cost of more processing time and sometimes, if not used wisely, the perfor-

mance can be even worse. In this paper we present the results of a comparison between various combinations

of region detectors and descriptors. The test performed consists in computing the essential matrix between

panoramic images using correspondences established with these methods. Different combinations of region

detectors and descriptors are evaluated and validated using ground truth data. The results will help us to ﬁnd

the best combination to use it in an autonomous robot navigation system.

1 INTRODUCTION

Autonomous robot navigation is one of the most chal-

lenging problems of mobile robotics and, although it

has been widely studied, it is far from being solved

completely. To date, the most successful approaches

are a set of techniques known as SLAM (Simul-

taneous Localization And Mapping) (Thrun, 2002).

These methods consist in iteratively searching for an

optimal solution to both problems: self localization

and map building. SLAM methods can be classiﬁed

amongst three main categories: metric SLAM, for

methods that give an accurate localization and map-

ping (Thrun, 2002; Castellanos and Tardos, 2000);

topologic SLAM, where the environment is usually

represented as a graph of “places” and the connectiv-

ity information amongst them (Tapus and Siegwart,

2006); and ﬁnally hybrid approaches, which try to

combine the advantages of both techniques and re-

duce their drawbacks (Tomatis et al., 2002).

To correct the accumulative errors of odometry,

SLAM techniques use additional information from

the environment acquired with sensors like sonars,

laser range-scanners, etc. When a camera is used

to obtain such data, the method is known as Visual

SLAM. Recently, this approach has gained strength

thanks to the development of new computer vision

algorithms that extract discriminative and meaningful

information from the images. One promising line of

research consists in using invariant visual features

extracted from images to construct a map of the

environment and locate the robot in it (Se et al., 2001;

Booij et al., 2006; Ramisa et al., 2006). The core

of these methods consist in ﬁnding corresponding

features between two or more images acquired by the

robot and set up relations between the places where

this images were taken. One particularly interesting

subset of invariant features are the afﬁne covariant

regions, which can be correctly detected in a wide

range of acquisition conditions (Mikolajczyk et al.,

2005). Equally important are the local descriptors

such as SIFT (Lowe, 2004), which make the match-

ing of local regions acquired in different conditions

possible.

In (Ramisa et al., 2006), the authors developed a

topological localization method which uses constel-

lations of afﬁne covariant regions from a panoramic

292

Ramisa A., López de Mántaras R., Aldavert D. and Toledo R. (2007).

COMPARING COMBINATIONS OF FEATURE REGIONS FOR PANORAMIC VSLAM.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 292-297

DOI: 10.5220/0001642602920297

 SciTePress

image to describe a place (for example a room).

When a new panorama of features is acquired, it is

compared to all the stored panoramas of the map, and

the most similar one is selected as the location of the

robot. Using different types of feature detectors and

descriptors simultaneously increases the probability

of ﬁnding good correspondences, but at the same time

can cause other problems, such as more processing

time and more false correspondences. As means

to improve the results of their approach, in this

article various of these covariant region detectors

and descriptors are compared. Our objective is to

evaluate the performance of different combinations of

these methods in order to ﬁnd the best one for visual

navigation of an autonomous robot. The results of

this comparison will reﬂect the performance of these

detectors and descriptors under severe changes in

the point of view in a real ofﬁce environment. With

the results of the comparison, we intend to ﬁnd the

combination of detectors and descriptors that gives

better results with widely separated views.

The remainder of the paper is organized as fol-

lows. Section 2 provides some background informa-

tion in afﬁne covariant region detectors and descrip-

tors. Section 3 explains the experimental setup used

in the comparison and section 4 presents the results

obtained. Finally, in section 5 we close the paper with

the conclusions.

2 DETECTORS AND

DESCRIPTORS

Afﬁne covariant regions can be deﬁned as sets of pix-

els with high information content, which usually cor-

respond to local extrema of a function over the im-

age. A requirement for these type of regions is that

they should be covariant with transformations intro-

duced by changes in the point of view, which makes

them well suited for tasks where corresponding points

between different views of a scene have to be found.

In addition, its local nature makes them resistant to

partial occlusion and background clutter.

Various afﬁne covariant region detectors have

been developed recently. Furthermore, different

methods detect different types of features, for ex-

ample Harris-Afﬁne detects corners while Hessian-

Afﬁne detects blobs. In consequence, multiple re-

gion detectors can be used simultaneously to increase

the number of detected features and thus of potential

matches.

However, using various region detectors can also

introduce new problems. In applications such as VS-

LAM, storing an arbitrary number of different afﬁne

covariant region types can increase considerably the

size of the map and the computational time needed

to manage it. Another problem may arise if one of

the region detectors or descriptors gives rise to a high

amount of false matches, as the mismatches can con-

fuse the model ﬁtting method and a worse estimation

could be obtained.

Recently Mikolajczyk et al. (Mikolajczyk et al.,

2005) reviewed the state of the art of afﬁne covari-

ant region detectors individually. Based on Mikola-

jczyk et al. work, we have chosen three types of afﬁne

covariant region detectors for our evaluation of com-

binations: Harris-Afﬁne, Hessian-Afﬁne and MSER

(Maximally Stable Extremal Regions). These three

region detectors have a good repeatability rate and a

reasonable computational cost.

Harris-Afﬁne ﬁrst detects Harris corners in the

scale-space using the approach proposed by Linde-

berg (Lindeberg, 1998). Then the parameters of an

elliptical region are estimated minimizing the differ-

ence between the eigenvalues of the second order mo-

ment matrix of the selected region. This iterative pro-

cedure ﬁnds an isotropic region, which is covariant

under afﬁne transformations.

The Hessian-Afﬁne is similar to the Harris-Afﬁne,

but the detected regions are blobs instead of corners.

Local maximums of the determinant of the Hessian

matrix are used as base points, and the remainder of

the procedure is the same as the Harris-Afﬁne.

The Maximally Stable Extremal region detector

proposed by Matas et al. (Matas et al., 2002) detects

connected components where the intensity of the pix-

els is several levels higher or lower than all the neigh-

boring pixels of the region.

Matching local features between different views

implicitly involves the use of local descriptors. Many

descriptors with wide-ranging degrees of complexity

exist in the literature. The most simplest descriptor

is the region pixels alone, but it is very sensitive to

noise and illumination changes. More sophisticated

descriptors make use of image derivatives, gradient

histograms, or information from the frequency do-

main to increase the robustness.

Recently, Mikolajczyk and Schmid published a

performance evaluation of various local descriptors

(Mikolajczyk and Schmid, 2005). In this review more

than ten different descriptors are compared for afﬁne

transformations, rotation, scale changes, jpeg com-

pression, illumination changes, and blur. The conclu-

sions of their analysis showed an advantage in per-

formance of the Scale Invariant Feature Transform

(SIFT) introduced by Lowe (Lowe, 2004) and one of

its variants: Gradient Location Orientation Histogram

COMPARING COMBINATIONS OF FEATURE REGIONS FOR PANORAMIC VSLAM

293

(GLOH) (Mikolajczyk and Schmid, 2005). Based on

these results, we use these two local descriptors in our

experiments. Both SIFT and GLOH descriptors di-

vide the afﬁne covariant region in several subregions

and construct a histogram with the orientations of the

gradient for each subregion. The output of both meth-

ods is a 128-dimension descriptor vector computed

from the histograms.

3 EXPERIMENTAL SETUP

In this section, we describe our experimental setup.

The data set of images is composed of six sequences

of panoramas from different rooms of our research

center. Each sequence consists of 11 to 25 panoramas

taken every 20 cm. moving along a straight line prede-

ﬁned path. The panoramas have been constructed by

stitching together multiple views taken from a ﬁxed

optical center with a Directed Perception PTU-46-70

pan-tilt unit and a Sony DFW-VL500 camera.

Apart from the changes in point of view, the

images exhibit different problems such as illumina-

tion changes, repetitive textures, wide areas with no

texture and reﬂecting surfaces. These nuisances are

common in uncontrolled environments.

From each panorama, a constellation of afﬁne co-

variant regions is extracted and the SIFT and the

GLOH descriptors are computed for each region. In

Figure 1 a fragment of a panorama with several de-

tected Hessian-Afﬁne regions can be seen.

To ﬁnd matches between the feature constellations

of two panoramas, the matching method proposed by

Lowe in (Lowe, 2004) is used. According to this strat-

egy, one descriptor is compared using euclidean dis-

tance with all the descriptors of another constellation,

and the nearest-neighbor wins. Bad matches need to

be rejected, but a global threshold on the distance

is impossible to be found for all situations. Instead,

Lowe proposes to compare the nearest-neighbor and

the second nearest-neighbor distances and reject the

point if the ratio is greater than a certain value, which

typically is 0.8. Lowe determined, using a database

of 40,000 descriptors, that rejecting all matches with

a distance ratio higher than this value, 90% of the

false matches were eliminated while only 5% of cor-

rect matches were discarded.

Finally, the matches found comparing the de-

scriptors of two constellations are used to estimate

the essential matrix between the two views with the

RANSAC algorithm. As in the case of conventional

cameras, the essential matrix in cylindrical panoramic

cameras veriﬁes,

⊤

= 0, (1)

where p

and p

are projections of a scene point P

in the two cylindrical images related by the essential

matrix E. However, the epipolar constraint deﬁnes a

sinusoid instead of a line. This sinusoid can be pa-

rameterized with the following equation,

(φ) = −

cos(φ) + n

sin(φ)

, (2)

where z

(φ) is the height corresponding to the an-

gle φ in the panorama, n

= [n

, n

] is the epipolar

plane normal, obtained with the following expression,

= p

⊤

E. (3)

The test performed consists in estimating the es-

sential matrix between the ﬁrst panorama of the se-

quence and all the remaining panoramas using dif-

ferent combinations of detectors and descriptors. As

random false matches will rarely deﬁne a widely sup-

ported epipolar geometry, ﬁnding a high number of

inliers reﬂects a good performance. To validate the

results, ground truth essential matrices between the

reference image and all the other images of each

sequence have been computed using manually se-

lected corresponding points. These essential matrices

are then used to compute the error of the inliers of

each combination of detectors and descriptors to the

ground truth epipolar sinusoid.

Figure 1: Some Hessian-Afﬁne regions in a fragment of a

panorama.

4 RESULTS

To evaluate the performance of each combination

of methods, we measured the maximum distance at

which each combination of methods passed the three

different tests that are explained in the following para-

graph. The results of the tests are presented in the Ta-

ble 1. It is important to notice that these distances are

the mean across all the panorama sequences.

Since a minimum of 7 inliers are required in or-

der to ﬁnd the essential matrix, the ﬁrst test shows

at which distance each method achieves less than 7

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

294

inliers. For the second test, the inliers that do not fol-

low equation 1 for the ground truth essential matri-

ces are rejected as false matches. Again, the distance

at which the number of correct inliers drops below 7

is checked. Finally, the third test evaluates at which

distance the percentage of correct inliers drops below

50%, which is the theoretic breakdown point for the

RANSAC algorithm. This third test is the hardest and

the more realistic one.

Table 1: Results of the comparison. For convenience

we have labeled M:MSER, HA:Harris-Afﬁne, HE:Hessian-

Afﬁne, S:SIFT, G:GLOH.

Test 1 Test 2 Test 3

M+G 180cm 140cm 83cm

HA+G 320cm 200cm 106cm

HE+G 380cm 220cm 108cm

M+S 180cm 120cm 84cm

HA+S 400cm 220cm 101cm

HE+S 480cm 200cm 107cm

M+HE+G 480cm 200cm 106cm

HA+HE+G 480cm 220cm 100cm

M+HA+G 480cm 220cm 99cm

M+HE+S 480cm 180cm 99cm

HA+HE+S 480cm 260cm 111cm

M+HE+S 480cm 220cm 109cm

M+HA+HE+G 480cm 240cm 87cm

M+HA+HE+S 480cm 260cm 82cm

The results of the ﬁrst test show that, except for

the Hessian-Afﬁne and SIFT, the combination of

various detectors performs better than one detector

alone. In the second test we can see that the per-

formance of all the methods is greately reduced,

and the combination of two methods (except for the

Harris-Afﬁne, Hessian-Afﬁne and SIFT) drops to a

similar level to that of one method alone. Finally,

regarding the third test, the performance drops again,

putting all combinations at a similar level (around

100 cm). For the third test an exponential function

has been ﬁtted to the data sets to aproximate the

behaviour of the noisy data and ﬁnd the estimated

point where the ratio falls below 0.5.

In Figure 2 the ratio of inliers for the best

combinations of each category is shown (namely,

Harris-Afﬁne and GLOH, Hessian-Afﬁne and Harris-

Afﬁne and SIFT, and all the detectors and GLOH)

as well as the ﬁtted exponential of each of the three

combinations. As can be observed in the point’s

cloud, the method using two regions in general

achieved better results than the other two methods,

and several times achieved a performance above 0.5

after the estimated point.

0 50 100 150 200 250 300 350 400 450 500

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

cm.

One Region

Two Regions

Three Regions

Figure 2: Ratio of inliers for the best combinations of one

region (Hessian-Afﬁne and GLOH), two regions (Harris-

Afﬁne and Hessian-Afﬁne and SIFT) and three regions

(MSER, Harris-Afﬁne, Hessian-Afﬁne and GLOH). Addi-

tionally, the exponential ﬁtting of the different data sets is

shown.

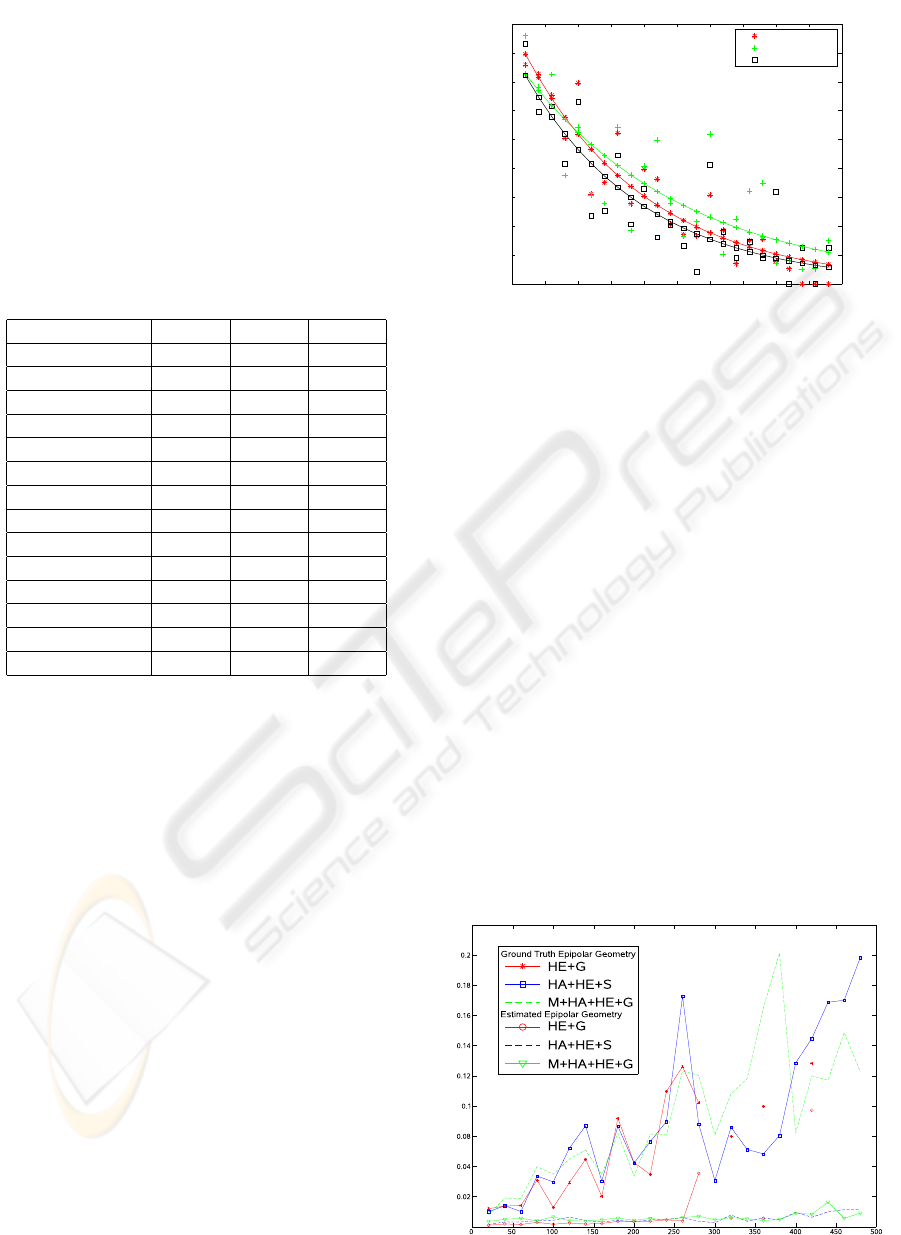
To obtain an estimation of the precision, the

mean distance error of the inliers to the estimated

epipolar sinusoid and the corresponding ground truth

epipolar sinusoid has been computed for the three

selected combinations (Hessian-Afﬁne and GLOH,

Hessian-Afﬁne and Harris-Afﬁne and SIFT, and

all the detectors and GLOH). The results of this

comparison are presented in ﬁgure 3. It can be seen

that for the ﬁrst 250 cm. all the methods have a

similar error, both for the estimated epipolar sinusoid

and for the ground truth one. Discontinuities are due

to failures of the combinations to compute a valid

essential matrix at a given distance.

Finally, a performance test has been done to com-

pare the processing speed of the different region de-

tectors and descriptors. This results, shown in Table

Figure 3: Mean distance error of a match to the estimated

epipolar sinusoid and to the ground truth epipolar sinusoid.

COMPARING COMBINATIONS OF FEATURE REGIONS FOR PANORAMIC VSLAM

295

2, are the mean of 50 runs of a 4946x483 panoramic

image. The implementation used to perform the tests

is the one given in

http://www.robots.ox.ac.uk/

vgg/research/affine/

by the authors of the dif-

ferent region detectors (Mikolajczyk et al., 2005). It

is important to note that this implementations are not

optimal, and a constant disk reading and writting time

is entailed. The tests where done in a AMD Athlon

3000MHz computer.

Table 2: Time Comparision of the different region detectors

and descriptors.

Time (sec) Regions Processed

MSER 0.95 828

Harris-Afﬁne 8.47 3379

Hessian-Afﬁne 3.34 1769

SIFT 14.87 3379

GLOH 16.64 3379

5 CONCLUSIONS

In this paper, we have evaluated different combina-

tions of afﬁne covariant region detectors and descrip-

tors to correclty estimate the essential matrix between

pairs of panoramic images. It has been shown that the

direct combination of region detectors ﬁnds a higher

number of corresponding points but this, in general,

does not translate in a direct improvement of the ﬁnal

result, because also a higher number of new outliers

are introduced.

No signiﬁcant differences in performance have

been found between the detectors individually, except

that MSER is notably faster than the other methods

thanks to its very simple algorithm; nevertheless the

detected regions are very robust. However MSER

ﬁnds a low number of regions and, as the robot moves

away from the original point, the matches become to

few to have a reliable estimation of the essential ma-

trix. Regarding combinations of two region detectors,

they ﬁnd estimations of the essential matrix at longer

distances. However, as shown in the results, the dis-

tance at which the estimations are reliable is similar to

that of one detector alone. Finally, the combinations

of three descriptors have shown to perform worse than

the combinations of two. The reason is probably the

number of false matches, that confuse the RANSAC

method.

Regarding the descriptors, no signiﬁcant differ-

ences have been found between the SIFT and the

GLOH. The GLOH gives a slightly better perfor-

mance than the SIFT, but also requires a bit more pro-

cessing time.

Additionally we have found the practical limits in

distance between the panoramic images in order to

have a reliable estimation using these methods. This

value can be used as the distance that a robot using

this method to navigate in an ofﬁce environment is

allowed to travel before storing a new node in the

map.

Future work includes experimentig with a larger

data set and with different kinds of environments to

verify and extend the presented results. Another in-

teresting line of continuation would be investigating

better matching and model ﬁtting methods to reduce

the proportion of false matches, and also researching

ways to combine the different types of regions taking

into account the scene content or estimated reliability

of each region detector.

ACKNOWLEDGEMENTS

The authors want to thank Adriana Tapus for her valu-

able comments and help. This work has been par-

tially supported by the FI grant from the Generali-

tat de Catalunya, the European Social Fund and the

MID-CBR project grant TIN2006-15140-C03-01 and

FEDER funds.

REFERENCES

Booij, O., Zivkovic, Z., and Kr

ose, B. (2006). From sensors

to rooms. In Proc. IROS Workshop From Sensors to

Human Spatial Concepts, pages 53–58. IEEE.

Castellanos, J. A. and Tardos, J. D. (2000). Mobile Robot

Localization and Map Building: A Multisensor Fu-

sion Approach. Kluwer Academic Publishers, Nor-

well, MA, USA.

Lindeberg, T. (1998). Feature detection with automatic

scale selection. Int. J. Comput. Vision, 30(2):79–116.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. Interantional Journal of Com-

puter Vision, 60(2):91–110.

Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002). Ro-

bust wide baseline stereo from maximally stable ex-

tremal regions. In Proceedings of the British Machine

Vision Conference 2002, BMVC 2002, Cardiff, UK,

2-5 September 2002. British Machine Vision Associ-

ation.

Mikolajczyk, K. and Schmid, C. (2005). A perfor-

mance evaluation of local descriptors. IEEE Trans-

actions on Pattern Analysis & Machine Intelligence,

27(10):1615–1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L. V.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

296

(2005). A comparison of afﬁne region detectors. Inter-

national Journal of Computer Vision, 65(1/2):43–72.

Ramisa, A., Aldavert, D., and Toledo, R. (2006). A

panorama based localization system. In 1st CVC Re-

search and Development Workshop, 2006, pages 36–

41. Computer Vision Center.

Se, S., Lowe, D., and Little, J. (2001). Vision-based

mobile robot localization and mapping using scale-

invariant features. In Proceedings of the IEEE In-

ternational Conference on Robotics and Automation

(ICRA), pages 2051–2058, Seoul, Korea.

Tapus, A. and Siegwart, R. (2006). A cognitive modeling

of space using ﬁngerprints of places for mobile robot

navigation. In Proceedings the IEEE International

Conference on Robotics and Automation (ICRA), Or-

lando, U.S.A., May 2006.

Thrun, S. (2002). Robotic mapping: A survey. In Lake-

meyer, G. and Nebel, B., editors, Exploring Artiﬁ-

cial Intelligence in the New Millenium. Morgan Kauf-

mann.

Tomatis, N., Nourbakhsh, I., and Siegwart, R. (2002).

Hybrid simultaneous localization and map building:

Closing the loop with multi-hypotheses tracking. In

Proceedings of the IEEE International Conference on

Robotics and Automation (ICRA), Washington DC,

USA, May 2002.

COMPARING COMBINATIONS OF FEATURE REGIONS FOR PANORAMIC VSLAM

297