STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS

BASED ON THE DECOUPLED MULTIPLE MODEL APPROACH

Rodolfo Orjuela, Beno

ıt Marx, Jos

e Ragot and Didier Maquin

Centre de Recherche en Automatique de Nancy, UMR 7039, Nancy-Universit

e, CNRS

2, Avenue de la For

et de Haye, 54 516 Vandœuvre-l

es-Nancy, France

Keywords:

State estimation, nonlinear discrete-time systems, multiple model approach, decoupled multiple model.

Abstract:

Multiple model approach is a powerful tool for modelling nonlinear systems. Two structures of multiple mod-

els can be distinguished. The ﬁrst structure is characterised by decoupled submodels, i.e. with no common

state (decoupled multiple model), in opposition to the second one where the submodels share the same state

(Takagi-Sugeno multiple model). A wide number of research works investigate the state estimation of nonlin-

ear systems represented by a classic Takagi-Sugeno multiple model. On the other hand, to our knowledge, the

state estimation of the decoupled multiple model has not been investigated extensively. This paper deals with

the state estimation of nonlinear systems represented by a decoupled multiple model. Conditions for ensuring

the convergence of the estimation error are formulated in terms of a set of Linear Matrix Inequalities (LMIs)

employing the Lyapunov direct method.

1 INTRODUCTION

Highly nonlinear processes are commonly encoun-

tered in practical engineering problems (chemistry,

mechanic, hydraulic, electrotechnics, etc). An accu-

rate model with a simple structure, preferably linear,

is often necessary for designing a control law or set-

ting up a diagnosis strategy using conventional con-

trol tools. Building only one model, valid in whole

operating space of the system, is not always possible

due, for example, to the change of the dynamic be-

haviour in the operating space. Hence, the operating

space of the system is often limited before the identi-

ﬁcation stage (local modelling).

New techniques of identiﬁcation have been devel-

oped for modelling the overall behaviour of the pro-

cess (global modelling). One of these techniques is

based on the decomposition of the operating space of

the system into a ﬁnite number of operating zones.

Each operating zone is characterised by a submodel

that has a simple structure. According to the zone

where the nonlinear system evolves, the output y

each submodel is more or less requested in order to

describe the global behaviour y of the nonlinear sys-

tem, that is to say:

y(k) =

∑

i=1

(k)y

(k), (1)

where the i

submodel contribution depends on the

weighting function µ

. A wide number of identiﬁ-

cation techniques based on this same principle can

be distinguished: piecewise linear model, radial ba-

sis function networks, fuzzy models, multiple models,

etc.

In this communication, we tackle the multiple

model approach. Classically, the multiple model is

built using linear submodels associated with weight-

ing functions that ensure a smooth blend between the

submodels. It is important to note that the multi-

ple models are considered as an universal approxima-

tion tool of nonlinear systems (Johansen et al., 2000).

Hence, it is possible to apply the available tools for

linear systems to nonlinear systems represented by a

multiple model.

In (Filev, 1991) two possible interpretations of

equation (1) have been investigated in a fuzzy mod-

elling framework (these interpretations will be di-

rectly related to multiple model). In the ﬁrst inter-

pretation, the submodels are decoupled and their state

vector is different (decoupled multiple model); in the

second one, the submodels have the same state vector

(Takagi-Sugeno multiple model).

The second interpretation has been widely popu-

larized and many works deal with the identiﬁcation

and analysis (control, state estimation, diagnosis, etc.)

of nonlinear systems represented by this class of mul-

142

Orjuela R., Marx B., Ragot J. and Maquin D. (2007).

STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE MODEL APPROACH.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 142-148

DOI: 10.5220/0001640101420148

 SciTePress

tiple model.

By comparison with the Takagi-Sugeno multi-

ple model, the decoupled multiple model has been

less investigated. Some works in control domain

(Gawthrop, 1995; Gatzke and Doyle III, 1999; Gre-

gorcic and Lightbody, 2000) and in identiﬁcation

(Venkat et al., 2003) of nonlinear systems have em-

ployed successfully this structure and shown its rele-

vance. However, to our knowledge the state estima-

tion problem has not been investigated.

In this paper, a new method for designing a state

estimator of nonlinear discrete-time systems repre-

sented by a decoupled multiple model is presented.

The paper starts with section 2 that introduces two

multiple model structures according to the selected

interpretation. Stability of decoupled multiple model

is investigated in section 3. In section 4, sufﬁcient

conditions (in LMIs terms) are established in order to

ensure the asymptotic convergence of the estimation

error. Finally, section 5 presents an academic example

of state estimation of a decoupled multiple model.

2 MULTIPLE MODEL

STRUCTURES

The interconnection of the submodels can be per-

formed with various structures in order to generate

the global output of the multiple model. Two essen-

tial structures of multiple models can be distinguished

whether the same state vector appears in all submod-

els or not.

Concerning the identiﬁcation step, there exists dif-

ferent techniques (linearisation, parametric optimisa-

tion) for the parameter estimation of the submod-

els for a particular multiple model structure. See

(Murray-Smith and Johansen, 1997; Gasso et al.,

2001; Venkat et al., 2003) and the references therein

for further information about these techniques.

2.1 Takagi-Sugeno Multiple Model

The Takagi-Sugeno multiple model structure is con-

ventionally employed in multiple model analysis and

synthesis (Murray-Smith and Johansen, 1997). This

multiple model has the following structure:

(k+ 1) = A

x(k) + B

u(k),

x(k+ 1) =

∑

i=1

(ξ(k))x

(k+ 1), (2)

y(k) =

∑

i=1

(ξ(k))C

x(k),

where x ∈ R

is the state vector, u ∈ R

the input

and y ∈ R

the output vector. For the i

submodel,

∈ R

n×n

is the system matrix, B

∈ R

n×m

the input

matrix andC

∈ R

p×n

the output matrix. The µ

are the

weighting functions with the following properties:

∑

i=1

(ξ(k)) = 1, ∀k (3a)

0 ≤ µ

(ξ(k)) ≤ 1 ∀i = 1...L, ∀k (3b)

ξ is the decision variable that depends, for example,

on the measurable state variable and/or input or output

of the system.

From equation (2), one can see that in the Takagi-

Sugeno multiple model there is a common state x that

couples all submodel states x

. Therefore the dimen-

sion of the state vectors must be identical for all the

submodels.

2.2 Decoupled Multiple Model

Another possible structure using a parallel intercon-

nection of the submodels is proposed in (Filev, 1991).

Here, this structure is slightly modiﬁed using a state

representation as follows:

(k+ 1) = A

(k) + B

u(k),

(k) = C

(k) (4)

y(k) =

∑

i=1

(ξ(k))y

(k),

where x

∈ R

and y

∈ R

are, respectively, the state

vector and the output vector for the i

submodel and

where u, y, ξ, A

∈ R

×n

, B

∈ R

×m

et C

∈ R

p×n

have been deﬁned in the previous section.

It should be noted that the global output of the

multiple model is given by a weighted sum of the

submodel outputs. The blending between the sub-

models is made through the static equation. There-

fore each submodel evolves independently in its own

state space according to the input control and its ini-

tial state.

It is obvious that the principal interest of this

structure is the decoupling between the submodels.

Indeed, in contrast to the Takagi-Sugeno multiple

model, in the decoupled multiple model the dimen-

sion of the state vector x

of each submodel can be dif-

ferent (of course the output vector dimension must be

identical). Therefore, this structure is well adapted for

modelling strongly nonlinear systems whose structure

varies with the operating zone.

Notation: The following notations will be used all

along this paper. P > 0 (P < 0) means P is a positive

(negative) deﬁnite matrix; P

denotes the transpose

of P. We shall simply write µ

(ξ(k)) = µ

(k).

STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE

MODEL APPROACH

143

3 STABILITY ANALYSIS

It is possible to rewrite the equations (4) using an aug-

mented state vector as follows:

x(k+ 1) =

Ax(k) +

Bu(k),

y(k) =

C(k)x(k), (5)

where:

A =







0 0 0 0

0 0 0

0 0 A

0 0

0 0 0

0 0 0 0 A







B =













C(k) =







(k)C







and x(k) = [

(k) ··· x

(k)

]

∈ R

, n =

∑

i=1

Comments

• The matrices

A and

B are partitioned block matri-

ces.

• The output matrix

C(k) is a partitioned blocks ma-

trix whose parameters vary with time. Indeed,

the weighting functions µ

(k) only affect the sub-

model outputs.

The stability of a decoupled multiple model can be

easily established by analysing the eigenvalues of the

matrix

A. Notice that the matrix

A is a block diagonal

matrix. Therefore, all eigenvalues of this matrix are

inside the unit circle if and only if all eigenvalues of

every matrices A

are inside the unit circle.

To sum up, a decoupled multiple model is stable

if and only if all submodels are stable, in contrast to

Takagi-Sugeno multiple model where the stability de-

pends not only on the stability of the submodels but

also on the weighting function values. In the sequel,

the multiple model is assumed to be stable.

4 STATE ESTIMATION

State estimation of Takagi-Sugeno multiple model has

been widely investigated in a stabilisation law control

design perspective (Tanaka and Sugeno, 1990; Feng

et al., 1997; Chadli et al., 2003; Guerra and Ver-

meiren, 2004). Indeed, most of the used control tech-

niques needs the state vector knowledge which is not

in general fully measurable.

The classically used state estimator is an extension

of the proportional (Luenberger) observer. However,

some other classes of state estimators have been de-

veloped, for example, sliding mode observers (Palm

and Bergstern, 2000) and unknown input observers

(Akhenak et al., 2004).

The Lyapunov second method is typically em-

ployed in order to establish the sufﬁcient convergence

conditions of the estimation error in terms of a set of

Linear Matrix Inequalities (LMIs) (Boyd et al., 1994)

which are solved using standard convex optimization

algorithms.

State estimation of decoupled multiple model has

been partially explored in a self-tuning control law

design perspective in (Gawthrop, 1995). Thanks to

the decoupling between the submodels, the observer

gains can be classically calculated under the assump-

tion that the submodel outputs are known. However,

in our case, it is assumed that this information is not

available. Therefore, this approach cannot be used

here.

The aim of this section is to investigate the state

estimation of a decoupled multiple model, using only

the measurable signals i.e. the input and the output of

the system (the outputs of the submodels are not avail-

able). It is important to notice that the design of the

observer must take into account the blending between

the outputs of the submodels in order to guarantee the

convergence of the estimation error.

4.1 Observer Structure

The proportional gain observer for the decoupled

multiple model is given by:

ˆx

(k+ 1) = A

ˆx

(k) + B

u(k) + K

(y(k) − ˆy(k)),

ˆy

(k) = C

ˆx

(k), (6)

ˆy(k) =

∑

i=1

(k) ˆy

(k),

where ˆx

∈ R

is the state estimation for the i

sub-

model, y(k) the output of the multiple model, ˆy(k) the

output estimation and K

∈ R

×p

the gain of the i

observer. Equation (6) can be written in a compact

form using the partitioned matrices (5):

ˆx(k+ 1) = A

obs

(k) ˆx(k) +

Bu(k) +

Ky(k),

ˆy(k) =

C(k) ˆx(k), (7)

where

K = [

··· K

]

, (8)

obs

(k) =

A−

C(k). (9)

Note that the matrix A

obs

(k) may be decomposed as

follows:

obs

(k) =

∑

i=1

(k)Φ

, (10)

A−

, (11)

where

is the following partitioned block matrix:



0 ... C

.. . 0



. (12)

The design of the observer consists in determining

the gain

K such that the estimation error given by:

e(k) = x(k) − ˆx(k), (13)

converges asymptotically to zero for an arbitrary

blending between the submodel outputs.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

144

4.2 Estimation Error Convergence

Here, the second Lyapunov method is used to inves-

tigate the estimation error convergence by means of

a quadratic Lyapunov function. It is clear that other

Lyapunov functions can be considered (see section

4.4). The following Theorem gives a sufﬁcient con-

dition for ensuring the estimation error convergence.

Theorem 1. Consider the decoupled multiple model

(4) and the observer (6). The asymptotic convergence

towards zero of the estimation error is guaranteed if

there exists a symmetric and positive deﬁnite matrix P

and a matrix G such that:



P−

A− G



> 0, i = 1...L, (14)

where the observer gain is deduced from

K = P

−1

Proof. Let us consider the following quadratic Lya-

punov function:

V(e(k)) = e

(k)Pe(k), P = P

andP > 0. (15)

The variation of the above function is given by:

∆V(e(k)) = V(e(k+ 1)) −V(e(k)), (16)

∆V(e(k)) must be negative in order to ensure its de-

crease and the asymptotic error convergence also.

Considering the dynamics of the estimation error

given by:

e(k+ 1) = A

obs

(k)e(k), (17)

and substituting (15) and (17) into (16), then

∆V(e(k)) becomes:

∆V(e(k)) = e

(k){A

obs

(k)PA

obs

(k) − P}e(k), (18)

that is a quadratic form in e(k). Therefore,

a necessary and sufﬁcient condition for ensuring

∆V(e(k)) < 0 is:

obs

(k)PA

obs

(k) − P < 0, ∀k. (19)

By considering (10), the inequality (19) can be rewrit-

ten as:

∑

j=1

(k)Φ

−1

∑

i=1

(k)Φ

− P < 0, (20)

Combining the Schur complement with property (3a)

of the weighting functions, it is possible to write:

∑

i=1

(k)



P Φ

PΦ



> 0. (21)

The inequality (21) can be upper bounded using the

property (3b) of the weighting functions. Finally, a

sufﬁcient condition that ensures the error convergence

is given by:



P Φ

PΦ



> 0 i = 1...L (22)

and substituting (11) for Φ

, we obtain:



P (

A−

)

A−

) P



> 0, i = 1...L. (23)

These matrix inequalities are nonlinear in

K and P.

Therefore, it is not possible to solve them directly us-

ing classical LMI tools. The following change of vari-

ables G = P

K allows the linearisation of this problem

and ends the demonstration of Theorem 1.

4.3 Eigenvalue Placement

In order to enforce dynamic performances of the ob-

server (for example, the damping and the estimation

error decay rate) the eigenvalue placement of the ob-

server must be investigated. In (Chilali and Gahinet,

1996) a general characterization for eigenvalues clus-

tering in subregions of the complex plan in terms of

LMIs is proposed.

The eigenvalues of the matrix X are placed inside

the circle with radius R and centred at (q,0) in the z

plan if the following LMI is feasible:



−RP −qP+ XP

−qP+ (XP)

−RP



< 0, (24)

where P is a symmetric and positive deﬁnite matrix.

Let us notice that if R = 1 and q = 0 then we obtain the

stability condition for linear discrete-time systems.

In order to place the eigenvalues of the observer,

the LMIs of Theorem 1 are modiﬁed as follows.

Theorem 2. Consider the decoupled multiple model

(4) and the observer (6). The eigenvalues of the ob-

server are placed inside the circle with radius R and

centred at (q,0) if there exists a symmetric and posi-

tive deﬁnite matrix P and a matrix G such that:



−RP −qP+

P−

−qP+ P

A− G

−RP



< 0, (25)

for i = 1...L, where the observer gain is given by

K = P

−1

It is clear that this Theorem coincides with The-

orem 1 if R = 1 and q = 0. In order to avoid strong

oscillations of the estimation error, the real part of the

eigenvalues of the observer are placed in the positive

zone of the unit circle and their imaginary part must

be reduced. A judicious choice of the radius R and

the centre (q,0), for example q = 0.5 and R = 0.45,

allows an appropriate placement of the eigenvalues of

the observer.

STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE

MODEL APPROACH

145

4.4 Relaxed Convergence Conditions

The asymptotic convergence conditions of the estima-

tion error, presented in the previous section, depend

on the existence of the common matrix P which sat-

isﬁes a set of LMIs. In general, when the multiple

model has a large number of submodels, the matrix P

cannot be found.

In order to reduce the conservatism of the con-

ditions obtained with a quadratic Lyapunov func-

tion, new candidate Lyapunov functions called non-

quadratic functions have been proposed. A wide

number of published works show the efﬁcient relax-

ation of the stability conditions provided by this class

of functions for a continuous time Takagi-Sugeno

multiple model (Jadbabaie, 1999; Rhee and Won,

2006) and also in the discrete time case (Guerra and

Vermeiren, 2004). The following Theorem gives a

sufﬁcient condition for ensuring the estimation error

convergence using a nonquadratic function.

Theorem 3. Consider the decoupled multiple model

(4) and the observer (6). The asymptotic convergence

towards zero of the estimation error is guaranteed if

there exists symmetric and positive deﬁnite matrices

and P

and a some matrix M and G such that:



A− G

)

A− G

M + M

− P



> 0 ∀i, j = 1...L, (26)

where the observer gain is deduced from

K = M

−1

Proof. The considered nonquadratic Lyapunov func-

tion is given by:

V(e(k)) = e

(k)

∑

i=1

(k)P

e(k) = e

(k)P(k)e(k), (27)

where P

= P

and P

> 0. The convergence error

analysis is performed as in the previous case. A nec-

essary and sufﬁcient condition in order to ensure the

error convergence is given by:

obs

(k)P(k + 1)A

obs

(k) − P(k) < 0. (28)

Introducing (10) and using the Schur complement, the

above inequality becomes:

∑

j=1

∑

i=1

(k)µ

(k+ 1)





> 0. (29)

Using property (3b) of the weighting functions and

substituting (11) for Φ

, one obtains the following suf-

ﬁcient condition that ensures the asymptotic conver-

gence of the estimation error:



(

A−

)

(

A−

) P



> 0, i, j = 1...L. (30)

Inequalities (30) are nonlinear matrix inequalities in

K, P

and P

. In contrast to the quadratic case, there is

not variable change that allows the direct linearisation

of this problem. However, the results coming from

(De Oliveira et al., 1999) (Theorem 2) help to rewrite

the inequalities (30) as follows:



(M(

A−

))

A−

) M + M

− P



> 0, i, j = 1...L,

where M is not constrained to be symmetric (M 6=

). After this transformation, the linearisation of

the above inequalities can be effectively yielded by

using the change of variables G = M

K. Hence, the

proof of Theorem 3 is completed.

Notice that Theorem 1 is encompassed by Theo-

rem 3. Indeed, if one sets P

= P

= M = P then the

Theorem 3 coincides with the Theorem 1. Therefore,

the previous result is less conservative than the condi-

tion obtained with a conventional quadratic function.

5 EXAMPLE

Let us consider the state estimation of the decoupled

multiple model with L = 3 submodels. The numerical

matrices A

, B

and C

are:



0.8 0

0.4 0.1



, A

−0.3 −0.5 0.2

0.7 −0.8 0

−2 0.1 0.7

, A



−0.5 0.1

−0.6 −0.5



= [

0.2 −0.4

]

, B

= [

0.7 −0.5 0.3

]

, B

= [

−0.2 0

]



0.7 0

0.5 0.2



, C



0.5 0 0.8

0.7 0.2 0.1



, C



0.9 0.3

−0.6 0



Here, the decision variable ξ is the input signal u(k) ∈

[0,1]. The weighting functions are obtained from nor-

malised Gaussian function:

(u(k)) = ω

(u(k))/

∑

j=1

(ξ(k)), (31)

(u(k)) = exp



−(u(k) −c

)

/σ



, (32)

with the standard deviation σ = 0.4 and the centre

= [0.1,0.5,0.9]. The eigenvalues of the matrix

A are inside the unit circle, thus the multiple model

is stable. Using Theorem 3, we obtain the following

observer gain:

K =



0.041 0.020 0.160 0.190 0.221 −0.090 −0.181

0.194 0.113 −0.299 −0.044 −0.701 0.172 0.268



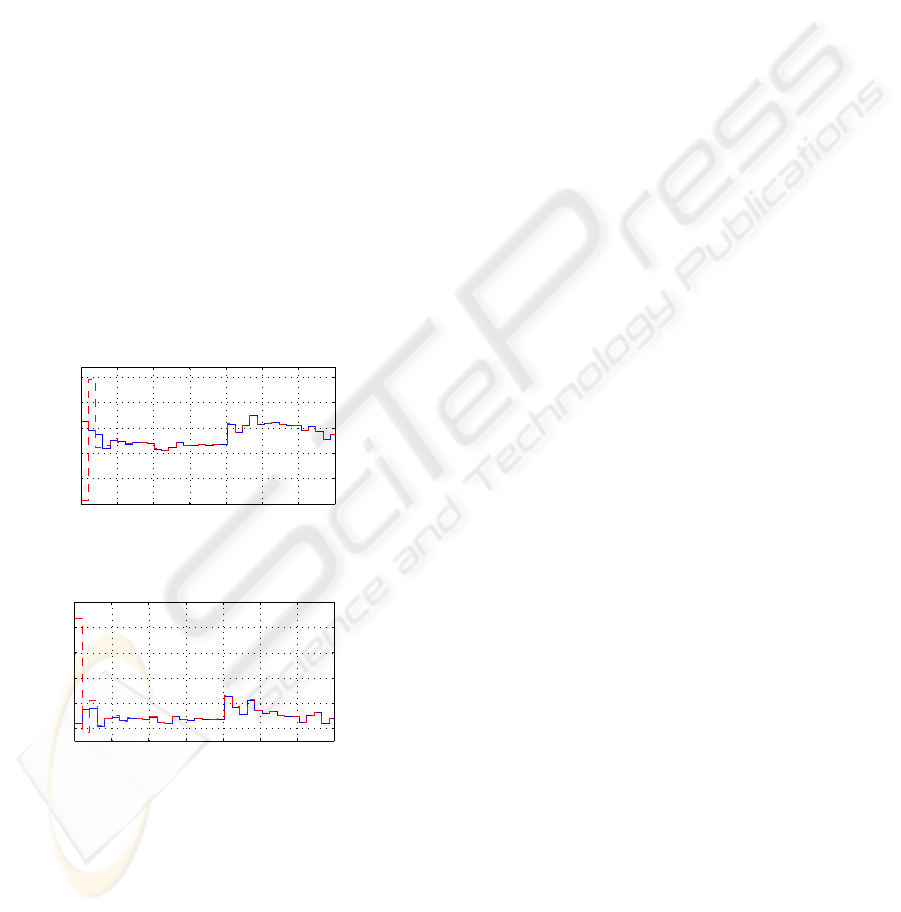
As can be seen in ﬁgures 1 and 2, the suggested ob-

server provides a good output estimation. The error

around the origin time is due to the different initial

conditions of the multiple model and the observer.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

146

6 CONCLUSION

A decoupled discrete time multiple observer has been

presented in order to proceed to the state estimation of

a class of nonlinear systems. The proposed observer

is an extension of the proportional observer used in

the linear observer theory.

Sufﬁcient conditions that guarantee the asymp-

totic convergence of the estimation error are given in

terms of a set of LMIs using a quadratic Lyapunov

function. Less conservative conditions are also pro-

posed thanks to a nonquadratic Lyapunov function.

In order to illustrate the performances of the proposed

observer an academic example is presented.

There are interesting prospects in control and di-

agnosis of nonlinear systems using this class of mul-

tiple model and observer. In particular, this observer

class may be useful for setting up a diagnosis strategy

for example. This task can be done with a bank of the

proposed observers that produce a set of residual sig-

nals useful for sensor fault detection and isolation. In

future work, the proposed approach will be extended

to other observer classes as proportional integral ob-

server or unknown input observer.

0 5 10 15 20 25 30 35

−1.5

−1

−0.5

0.5

Figure 1: Output y

of the multiple model (solid line) and

its estimated (dashed line).

0 5 10 15 20 25 30 35

0.2

0.4

0.6

0.8

Figure 2: Output y

of the multiple model (solid line) and

its estimated (dashed line).

REFERENCES

Akhenak, A., Chadli, M., Ragot, J., and Maquin, D. (2004).

Estimation of state and unknown inputs of a nonlinear

system represented by a multiple model. In 11h IFAC

Symposium on Automation in Mineral and Metal pro-

cessing, Nancy, France.

Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan, V.

(1994). Linear Matrix Inequalities in System and Con-

trol Theory. Philadelphia, P.A., SIAM studies in ap-

plied mathematics edition.

Chadli, M., Maquin, D., and Ragot, J. (2003). Multiple

observers for discrete-time multiple models. In Safe-

process, pages 801–806, Washington, D.C., USA.

Chilali, M. and Gahinet, P. (1996). H-inﬁnity design with

pole placement constraints: an LMI approach. IEEE

Transactions in Automatic and Control, 41(3):358–

367.

De Oliveira, M., Bernussou, J., and Geromel, J. (1999). A

new discrete-time robust stability condition. Systems

Control Letters,, 37(4):261–265.

Feng, G., Cao, S. G., Rees, N. W., and Chak, C. K. (1997).

Design of fuzzy control systems with guaranteed sta-

bility. Fuzzy Sets and Systems, 85(1):1–10.

Filev, D. (1991). Fuzzy modeling of complex sys-

tems. International Journal of Approximate Reason-

ing, 5(3):281–290.

Gasso, K., Mourot, G., and Ragot, J. (2001). Structure iden-

tiﬁcation in multiple model representation: elimina-

tion and merging of local models. In 40th IEEE Con-

ference on Decision and Control, pages 2992–2997,

Orlando, USA.

Gatzke, E. P. and Doyle III, F. J. (1999). Multiple model ap-

proach for CSTR control. In 14 IFAC World Congress,

pages 343–348, Beijing, P. R. China.

Gawthrop, P. (1995). Continuous-time local state lo-

cal model networks. In IEEE Conference on Sys-

tems, Man & Cybernetics, pages 852–857, Vancouver,

Canada.

Gregorcic, G. and Lightbody, G. (2000). Control of highly

nonlinear processes using self-tuning control and mul-

tiple/local model approaches. In 2000 IEEE Interna-

tional Conference on Intelligent Engineering Systems,

INES 2000, pages 167–171.

Guerra, T. M. and Vermeiren, L. (2004). LMI-based re-

laxed nonquadratic stabilization conditions for nonlin-

ear systems in the Takagi-Sugeno’s form. Automatica,

40(5):823–829.

Jadbabaie, A. (1999). A reduction in conservatism in stabil-

ity and L2 gain analysis of Takagi-Sugeno fuzzy sys-

tems via linear matrix inequalites. In 14h IFAC World

Congress, pages 285–289, Beijing, P. R. China.

Johansen, T., Shorten, R., and Murray-Smith, R. (2000).

On the interpretation and identiﬁcation of dynamic

Takagi-Sugeno fuzzy models. IEEE Trans. on Fuzzy

Systems, 8(3):297–313.

Murray-Smith, R. and Johansen, T. (1997). Multiple model

approaches to modelling and control. Taylor & Fran-

cis.

Palm, R. and Bergstern, P. (2000). Sliding mode observer

for a Takagi-Sugeno fuzzy system. In The Ninth IEEE

International Conference on Fuzzy Systems, volume 2,

pages 665–670, San Antonio.

STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE

MODEL APPROACH

147

Rhee, B. and Won, S. (2006). A new fuzzy Lyapunov func-

tion approach for a Takagi-Sugeno fuzzy control sys-

tem design. Fuzzy Sets and Systems, 157(9):1277–

1228.

Tanaka, K. and Sugeno, M. (1990). Stability analysis of

fuzzy systems using Lyapunov’s direct method. In

NAFIPS, pages 133–136, Toronto, Canada.

Venkat, A., Vijaysai, P., and Gudi, R. (2003). Identiﬁca-

tion of complex nonlinear processes based on fuzzy

decomposition of the steady state space. Journal of

Process Control, 13(6):473–488.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

148