TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED

MICROSCOPY

Silvie Luisa Br

azdilov

Faculty of Informatics, Masaryk University, Botanick

a 68a, Brno, Czech Republic

Keywords:

Fluorescence microscopy, focus function, genetic programming.

Abstract:

The results presented in this paper are twofold. First, autofocusing in automated microscopy is studied and

evaluated with respect to biomedical samples whose images can have more than one in-focus planes. While

the proposed procedure for ﬁnding the maximum of a focus function in a short time works satisfactorily, the

focus function itself is identiﬁed as the weakest link of the whole process.

Second, an interesting property of functions used for genetic programming, and an algorithm for generating

new individuals are introduced. Their usefulness and applicability are demonstrated on the problem of ﬁnding

a new focus function for automated autofocusing in microscopy.

1 INTRODUCTION

An automated microscope system is a powerful tool

for biomedical research, especially in ﬂuorescence

microscopy (Boddeke, 1999). The control of focus is

done through the use of motorized z-axis and an aut-

ofocus algorithm. The algorithm is an iterative pro-

cedure which steps along the z-axis to ﬁnd the plane

of the best focus. For each z-position an image is ac-

quired from which a focus value is computed accord-

ing to a certain focus function. Actually, the focus

function is a function of the z-position. It says how

sharp the image at the given z-position is. Ideally it

has one clear maximum whose position corresponds

to the z-position of the sharpest image.

According to (Groen et al., 1985) a useful focus

function should fulﬁl several criteria such as: uni-

modality, accuracy, reproducibility, insensitivity to

other parameters, the extremum be broadly tailed.

Although many focus algorithms have been pro-

posed and compared (Groen et al., 1985; Firestone

et al., 1991; Santos et al., 1997; Geusebroek et al.,

2000; Sun et al., 2004; Bueno-Ibarra et al., 2005), the

selection of an appropriate focus algorithm for spe-

ciﬁc conditions remains ad hoc and time consuming.

In ﬂuorescence microscopy weak light signals are

imaged in general and therefore more consideration

is needed in choosing a focus function compared to

bright ﬁeld microscopy. Due to the placement of the

objects (i. e., tissue or large cells) on the slides, the

thickness of the objects, and possible bending of the

slide, the objects normally do not lie in one plane

and hence the focus function is usually not unimodal.

This can consequently cause problems when search-

ing for the position of the maximum focus, because

many methods, such as Boddeke’s algorithm (Bod-

deke et al., 1994), rely on unimodality of the focus

function.

This paper is based on experiments with auto-

focusing simulated on a personal computer in the

MATLAB environment. The results of these exper-

iments are: assessment of current focus functions ap-

plied on special biomedical data; a proposed modiﬁ-

cation to existing autofocusing algorithm and its eval-

uation; and a method based on genetic programming

designed for ﬁnding a suitable focus function espe-

cially for similar image data.

1.1 Materials and Methods

The data used were TOPRO-dyed high-resolution im-

ages of desmocytes. They were acquired in either

confocal or standard (non-confocal) mode.

440

Luisa Brázdilová S. (2007).

TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED MICROSCOPY.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 440-447

DOI: 10.5220/0001639704400447

 SciTePress

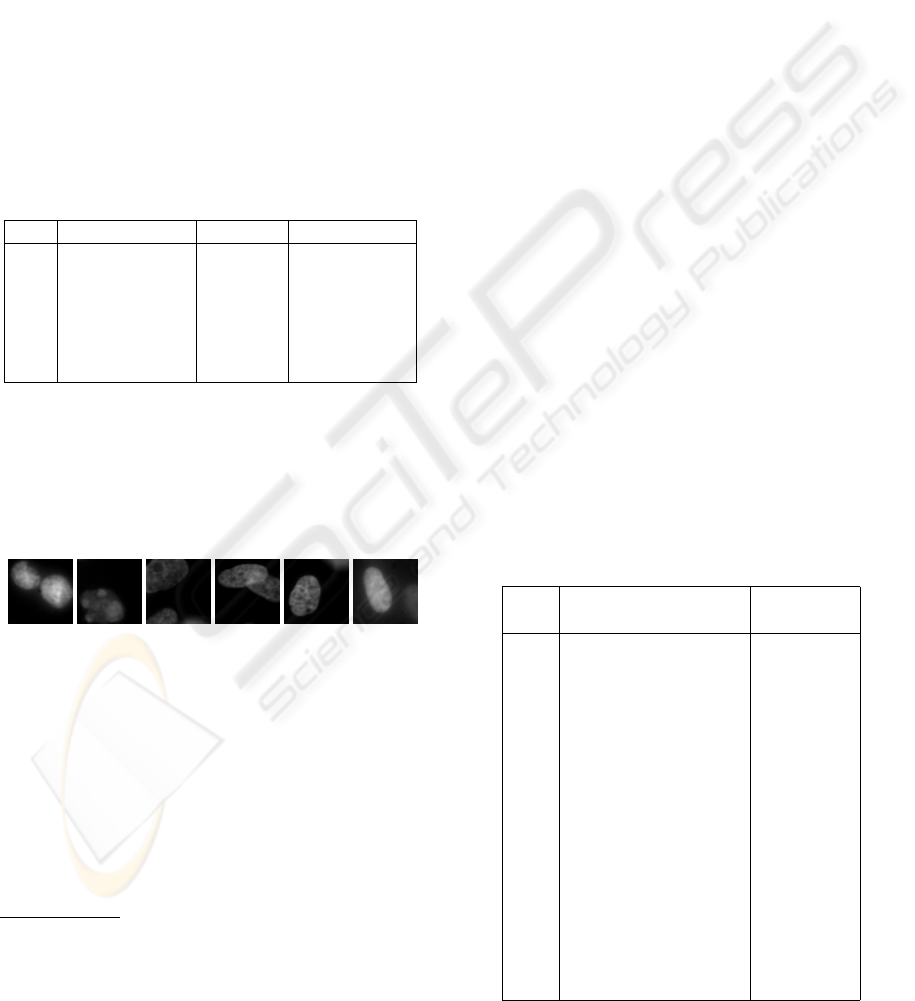
Cut outs 200× 200 pixels

from 6 different sam-

ples were used for the experiments in order to reduce

the time consumption. Each sample was acquired 99

times, once for each z-position. The size of the step

between two successive images was manually cho-

sen so that all the information needed for experiments

would be captured. It was also dependent on whether

the confocal mode was used or not. The z-positions

are described by their natural order and treated as

nondimensional values without respect to the step size

used.

The information about the images is summarized

in Table 1. In the last column there are the z-positions

that are considered to be in focus. These numbers

come from human perception and will be used as a

reference.

Table 1: Information about image samples used for experi-

ments.

No. Step size (µm) Mode In-focus pos.

1 0.5 standard 53

2 0.5 confocal 33

3 0.2 confocal 43

4 0.2 confocal 42

5 0.5 confocal 47

6 1.0 standard 45

A technique called binning

(Netten, 1997;

Kozubek et al., 1999; Boddeke et al., 1994) was ap-

plied on the samples. It is useful not only for reducing

the spatial frequency, but it also minimizes the pro-

cessing time

. The images after binning are presented

in Figure 1.

Figure 1: The in-focus images of testing samples 1 to 6 of

TOPRO-dyed high-resolution images of desmocytes, after

4× 4. binning.

2 STATE OF THE ART

In order to be able to implement an efﬁcient and ac-

curate autofocusing, a combination of a good focus

function and a robust procedure for searching for the

maximum is needed.

This size is sufﬁcient if suitable cut outs, i.e., those con-

taining cells or other objects of interest, are selected.

A group of adjacent pixes, here 4 × 4, is combined to

form a superpixel.

Now we have cut outs 50× 50 pixels.

2.1 Focus Functions

16 classic focus functions from the literature were

tested on the 6 samples (the list of these functions can

be found in the appendix). The functions were imple-

mented in MATLAB that is primarily optimized for

computations with matrices, and therefore they were

expressed using MATLAB-like functions with X be-

ing the acquired image. One of the main noticeable

changes is the introduction of 2D convolution instead

of pixel-wise operations that appear in the original no-

tation of the functions. More details about the new

notation will be given in section 4.

The error of a focus function is deﬁned as a differ-

ence between the focus position given by this function

and the reference focus position provided by human

experts (see Table 1). By comparison of the errors of

the focus functions under test, and after visual evalua-

tion of the shape of these focus functions (with respect

to the desired properties) it was concluded that ﬁve of

them are applicable for such biomedical data. The

two most suitable focus functions are the Variance

(see Appendix for the formula) that was expressed in

the form

div(sum(pow(minus(X,avg(X)),2)),area(X))

and the Vollath’s F5 function (also in Appendix) ex-

pressed in the form

minus(sum(times(X,conv(X,V1))),

sum(times(X,conv(X,V2))))

where

V1=(1 0 0)

and

V2=(1 0 0 0 0)

Nevertheless, none of them is fully satisfactory.

The mean error is never less than 4, the total error on

the six samples is 24 or more. Detailed results can be

found in Table 2.

Table 2: Errors of the 16 focus functions.

Func. Samples Total Mean

No. 1 2 3 4 5 6 error error

1 15 3 2 0 1 11 32 5.3

2 12 2 22 1 2 25 64 10.6

3 12 2 2 0 2 6 24 4.0

4 44 3 0 1 2 23 73 12.2

5 46 3 2 1 1 25 78 13.0

6 12 2 2 1 2 23 43 7.2

7 26 3 0 0 2 17 48 8.0

8 15 2 2 0 2 7 28 4.6

9 49 1 21 41 46 33 191 31.8

10 15 2 2 0 2 7 28 4.6

11 49 1 0 41 46 33 170 28.6

12 49 66 18 3 45 33 247 41.2

13 49 17 18 1 46 34 165 27.5

14 12 2 2 0 2 6 24 4.0

15 15 2 2 0 2 7 28 4.6

16 24 48 41 57 48 53 271 45.2

TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED MICROSCOPY

441

2.2 Algorithm for Finding the

Maximum Focus

For the purpose of automatic focusing we tested Bod-

deke’s algorithm (Boddeke et al., 1994). It was

originally designed for unimodal focus functions and

works in three phases as follows:

The algorithm starts with the coarse phase at an

arbitrary (but known) position z

. First, two samples

are acquired and their focus values are compared in

order to determine the direction towards the focus.

This may be a problem for focus functions with lo-

cal minima, such as those applied on images with two

or more natural in-focus planes. Then, more images

are acquired until the last focus value is lower than

the previous one. All the samples of the ﬁrst phase

are acquired evenly with the step ∆z

coarse

The starting position and the direction of the fol-

lowing ﬁne phase, which is based on the same princi-

ple as the coarse phase, are given by the results of the

coarse phase. The size step used during the ﬁne phase

is ∆z

fine

. Its size should correspond to the width of the

so-called quadratic region (see (Boddeke et al., 1994)

for details).

The last, reﬁne phase of Boddeke’s algorithm con-

sists of capturing N

refine

images around the position

of the maximum focus function value found so far,

ﬁtting a parabola and ﬁnding its maximum.

The tuning of such an algorithm is a difﬁcult goal:

it concerns multiobjective optimization as we want to

ﬁnd the values of several parameters (∆z

coarse

, ∆z

fine

refine

) while the number of images needs to be min-

imized and at the same time the accuracy and relia-

bility to be maximized. Moreover, the goal is to make

the algorithm robust to non-unimodal focus functions.

3 BODDEKE’S ALGORITHM

IMPROVEMENT

Here we present the proposed modiﬁcation of the al-

gorithm described in 2.2:

1. In the coarse phase two images are acquired with a

step ∆z

coarse

in order to ﬁnd the direction towards

the focus. Using the same step size, more images

are acquired until the last focus value is lower than

the previous one.

2. Interphase: the interval in which the focus lies is

assured by acquiring two images, one to each di-

rection, with a step ∆z

fine

from the z-position of

the highest focus so far. The position of the higher

focus function value of these two samples is the

direction towards the focus. This step may help

overcoming the bimodality that can occur.

3. In the ﬁne phase images are acquired until the last

focus value is lower than the previous one, with

the step size ∆z

fine

from the position and to the

direction determined by the previous phase. The

two z-positions of the highest focus function val-

ues are passed to the reﬁne phase.

4. The two z-positions from the ﬁne phase together

with three more (one in between and two on the

sides of the interval, all being equidistant) are

used for parabola ﬁtting. The maximum com-

puted from the parabola determines the position

of the maximum focus.

The following parameters were determined based on

empirical testing:

Table 3: Recommended parameters for the improved ver-

sion of Boddeke’s algorithm.

Parameter Value

∆z

coarse

∆z

fine

refine

The total number of images needed depends

strongly on the starting position z

. Yet some esti-

mation can be done, again based on some empirical

tests: it varies from 8 to 14. Naturally, starting near

to the in-focus position lowers the number of images

needed. The efﬁciency of this algorithm is shown

by the results of the algorithm applied together with

the Variance focus function on the all 6 samples pre-

sented in Table 4. For each sample, all 99 starting z-

positions were tested. The target is the position of the

actual maximum of the focus function, irrespectively

of the real in-focus position (we are assessing the al-

gorithm itself now, not the accuracy of the Variance

focus function, which is already known).

Table 4: Results of the improved version of Boddeke’s al-

gorithm using the Variance: ∆z

fine.

= 6, ∆z

coarse

= 10: a

comparison of target, mean and standard deviation values.

Sample 1 2 3 4 5 6

Target 68 35 41 42 49 52

Mean 68.9 35.1 42.2 41.9 48.2 53.5

Sted. dev. 0.30 0.54 0.60 0.30 1.18 4.62

It can be concluded that the improved Boddeke’s

algorithm is a reliable procedure for adaptive search-

ing the maximum of a function. If the focus function

was more accurate, we would have been able to locate

the position of the maximum focus quickly and pre-

cisely. Therefore, an effort should be made in order to

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

442

ﬁnd better focus function since the focus function is

currently the weakest link of the whole autofocusing.

4 FINDING THE FOCUS

FUNCTION

The focus functions developed up to now are based

on previous knowledge about the differences in in-

formation content in focused and unfocused image.

But the space of all focus functions is potentially in-

ﬁnite. Nevertheless, we are looking for functions that

are easy to compute. It means that these functions

should be composed of relatively small number of op-

erators and operands, such as the focus functions that

were invented up to date. Still there may be plenty

of other similar functions with unthought-of perfor-

mance. Genetic programming (Koza, 1992) is a ro-

bust technique suitable for searching for optimal so-

lution in a large state space. We will use it in an at-

tempt to ﬁnd a new focus function that will work well

on noisy biomedical images.

Genetic programming works in the same way as

genetic algorithms (Mitchell, 1996), but the popula-

tion is composed of functions (or programs), that can

be expressed in tree structure. The root represents the

output of the function, the leaves represent the argu-

ments. Inner nodes represent operators (here called

elementary functions).

Genetic programming, identically to the theory of

programming languages, faces the challenge of distin-

guishing between different data types. Strongly typed

genetic programming (Montana, 1995) is a branch of

genetic programming that ﬁnds inspiration in strongly

typed programming languages, when dealing with

this challenge. A modiﬁed version of this approach,

adapted especially for our data types needs, will be

presented here.

The MATLAB matrices of

doubles

are the only

data types used for our computations. However, we

need to work with matrices of any size, and distin-

guish between them. We will therefore deﬁne data

types by pairs of integers that will correspond to the

matrix sizes

. In addition, some functions have natu-

ral restrictions on the relations among the types (both

output and input). We will therefore deﬁne them as

generic functions (see (Montana, 1995)). Generic

functions are functions that are able to work with

more data types. They get instantiated during the tree

building. This approach needs special attention to be

paid during the process of tree generation (this will be

described in detail in next sections).

For example, a scalar will be of type (1, 1) etc.

Table 5: Table of functions, terminals and their types.

Function Arity Output Input 1 Input2

plus 2 a,b a,b a,b

minus 2 a,b a,b a,b

times 2 a,b a,b a,b

mtimes 2 a,c a,b b,c

nmtimes 2 a,b 1,1 a,b

mntimes 2 a,b a,b 1,1

divnum 2 a,b a,b 1,1

divmat 2 a,b a,b a,b

pownum 2 a,b a,b 1,1

conv 2 a,b a,b c,d

sum 1 1,1 a,b –

abs 1 a,b a,b –

avg 1 1,1 a,b –

log2 1 a,b a,b –

log10 1 a,b a,b –

uminus 1 a,b a,b –

area 1 1,1 a,b –

min 1 1,1 1,a –

max 1 1,1 1,a –

hist 1 256,1 a,b –

matrand 0 a,b – –

2 0 1,1 – –

X 0 x, y – –

If the type (or one of the pair components) is

generic, its value is represented by a symbolic value

denoted by alphabetic letters a, b, etc. The set of

symbolic values used for deﬁnition of a generic func-

tion represents the information we have at the moment

about relations among the type components. During

the process of creation of a new tree individual, there

is a moment when an elementary function is selected

for a node. If this elementary function is a generic

function, we may only deﬁne the input and output

types by symbolic values, but the important informa-

tion about the relation is preserved. For example, if a

binary function’s output must be of the same type as

its left-most input while the right-most input can be

arbitrary, we deﬁne output in terms of symbolic val-

ues (a, b), the left-most input also by (a, b), but the

right-most input is of type (c, d). The set of symbolic

values in this case is {a, b, c, d}. During instantiation,

each of these values is mapped to a speciﬁc numeric

value (e.g., 3, 8, 5 and 1), but the property that the

output type equals the right-most input’s type holds.

Of course, sets of symbolic values of different generic

elementary functions are totally independent (e.g., a

in the set of symbolic values of a function has noth-

ing to do with a belonging to the set of symbolic val-

ues of any other elementary function within the same

tree individual). Only when an elementary function

TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED MICROSCOPY

443

is assigned to a node that is direct descendant of an-

other one, its instantiated output type and the relevant

instantiated input type of the other function must ﬁt.

The aim is to have all the nodes fully instantiated after

the tree is generated. The result of crossover, mutation

etc. must be a valid function too.

The list of functions and terminals used together

with their types speciﬁcation is presented in Table 5.

The terminal set consists of a variable X that repre-

sents the image input (its size (x, y) is known in ad-

vance), and a constant 2 that occurs very often in the

classic focus functions. Function

matrand

of null par-

ity generates random matrices of desired size in the

program generation time. If the size is unspeciﬁed,

matrand

generates a matrix of random size between

(1, 1) and (10,10). Therefore its output type gets in-

stantiated on a random basis. Some functions have

predeﬁned type values from the deﬁnition: for ex-

ample, the function

sum

produces the sum of the el-

ements of an arbitrary matrix and therefore its output

type is ﬁxed and its value is (1, 1). The function

hist

computes the histogram with 256 bins. The function

area

gives the multiplication of matrix sizes,

conv

the 2D convolution of two matrices. The meaning of

other functions is straightforward.

4.1 Generation of a New Tree

The most complicated part of the process lies in man-

aging the data ﬂow during the instantiation. The fol-

lowing deﬁnition will be necessary:

Deﬁnition 4.1 A generic function is type-consistent

if and only if it holds that if all the input types are

fully instantiated, the output type is fully determined

as well.

An example of a function that does not fulﬁl this con-

dition is a unary function of which input type is (a, b)

and the output type is (c, d). The algorithm proposed

can work only on type-consistent functions.

The tree is built recursively, in a depth-ﬁrst man-

ner. The data structures used by the algorithm are:

The table of functions and terminals – The table

stores information about the generic functions and

their types in terms of symbolic or predeﬁned val-

ues, such as shown in Table 5. It is only read dur-

ing the process.

The function instances in the nodes – This data

structure is created at the same time when a node

is created. The information gets updated gradu-

ally. First, the name of the assigned elementary

function and its arity is stored here. Every time

a type component of this function instance is

instantiated, the value is stored here as well.

Investigating the node, it can be assumed what

types have already been instantiated.

The information ﬂow concerning the types is done in

four ways (Procedure A to D). Every time a new node

is created, its output type might, but does not have to,

be fully instantiated. (The root of any program that

aims to become a focus function falls among those

that have a speciﬁed output. It is the type (1, 1) be-

cause we want to measure a focus by a scalar value.)

Based on this information, a function is randomly se-

lected only from those that comply with the output

type request. The number of the direct descendants of

this node is now known.

The table of functions and terminals (Table 5) is

read ﬁrst in order to get the predeﬁned values of type

components, if there are any.

The components of the output type of the node are

checked. If any of them is already instantiated, the

symbolic values in the table are checked. If there is a

symbolic value for this component of the output type,

it means that we have instantiated it already. The spe-

ciﬁc value gets in the node to every type component

that has the same symbolic value in the table (proce-

dure B). The process can cause (partial) instantiation

of both the input and output types of the node.

The information known at that moment is pro-

cessed further when the left-most descendant is gen-

erated.

When the left-most subtree is completed, the pro-

cess of elaborating this node continues. Because of

the type consistence property the output type of the

left descendant must be fully instantiated at that mo-

ment. If the left input type has not been instanti-

ated before, it takes the value of the left-most descen-

dant’s output (Procedure C). This information may

enrich the information about other types in the ac-

tual node, therefore procedure D is needed: it goes

through the input types and if some of their values are

newly instantiated, the symbolic values in the table

are checked similarly to procedure B. The informa-

tion goes to other components (including the output

types) according to the symbolic value in the table.

The same process continues with all other descen-

dants, including procedures C and D. At the latest

when the last branch is ﬁnished, the output type of

the actual node is fully instantiated, owing to the type

consistent property and procedure D.

4.2 Genetic Programming Experiment

Description

We used GPLAB (Silva and Almeida, 2003b), a ge-

netic programmming toolbox for MATLAB, which

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

444

we modiﬁed in order to be able to handle strong typ-

ing. The initial population was generated using the

ramped half-and-half method (Koza, 1992). Dynamic

maximum tree depth, a technique for avoiding bloat

(Silva and Almeida, 2003a), was also incorporated.

The population size was 20, the dynamic limit and

maximum limit were 5 and 20, respectively.

Standard genetic operators

reproduction

mutation

and

crossover

were used. The type

constraint was resolved easily for mutation: a node

was randomly selected, its type was found and a

random tree was generated whose root’s output type

was the type needed. Crossover was performed only

if the node selected from the ﬁrst parent was present

at least once in the second parent as well. In the case

of multiple occurrence the ﬁnal node for exchange

was selected randomly.

The lexicographic parsimony pressure was used

for selection together with elitism.

Fitness function was computed in the following

way: ﬁrst, candidate focus function was evaluated

on the whole training set (an image sample acquired

with various z-positions). Then a maximum was

found, and the z-position that exhibits the maximum

value was compared with the reference z-position.

The difference is the error and therefore should be

minimized. To eliminate functions that are constant

around their maxima, the number of z-positions ex-

hibiting the maximum value was added to the ﬁtness

function to disrate functions with undesirable shape.

More training sets are needed in order to prevent

the genetic algorithm from guessing the correct z-

position independently on the image itself. Due to

high time consumption, the training set of three sam-

ples was used. It concerned samples 1, 3 and 6. The

remaining three samples were used for testing.

4.3 Results

The resulting functions were then compared with one

of the best classic functions, i. e. Variance, on a test-

ing set of three different samples. Five new functions

were giving comparable results. They even outper-

formed them on some samples. Their accuracy, i. e.,

how far a maximum was identiﬁed from the real one

on the z axis, was evaluated together with their shapes

and brevity.

One of the most interesting results is:

sum(plus(times(times(X,X),X),X))

which can be mathematically expressed as

f(z) =

∑

((I(x, y,z))

+ I(x, y, z))

The focus position given by that function is compared

to the output of Variance in Table 6. In three cases

(samples 3, 4 and 5) the genetic programming func-

tion was as successful as the two classic functions.

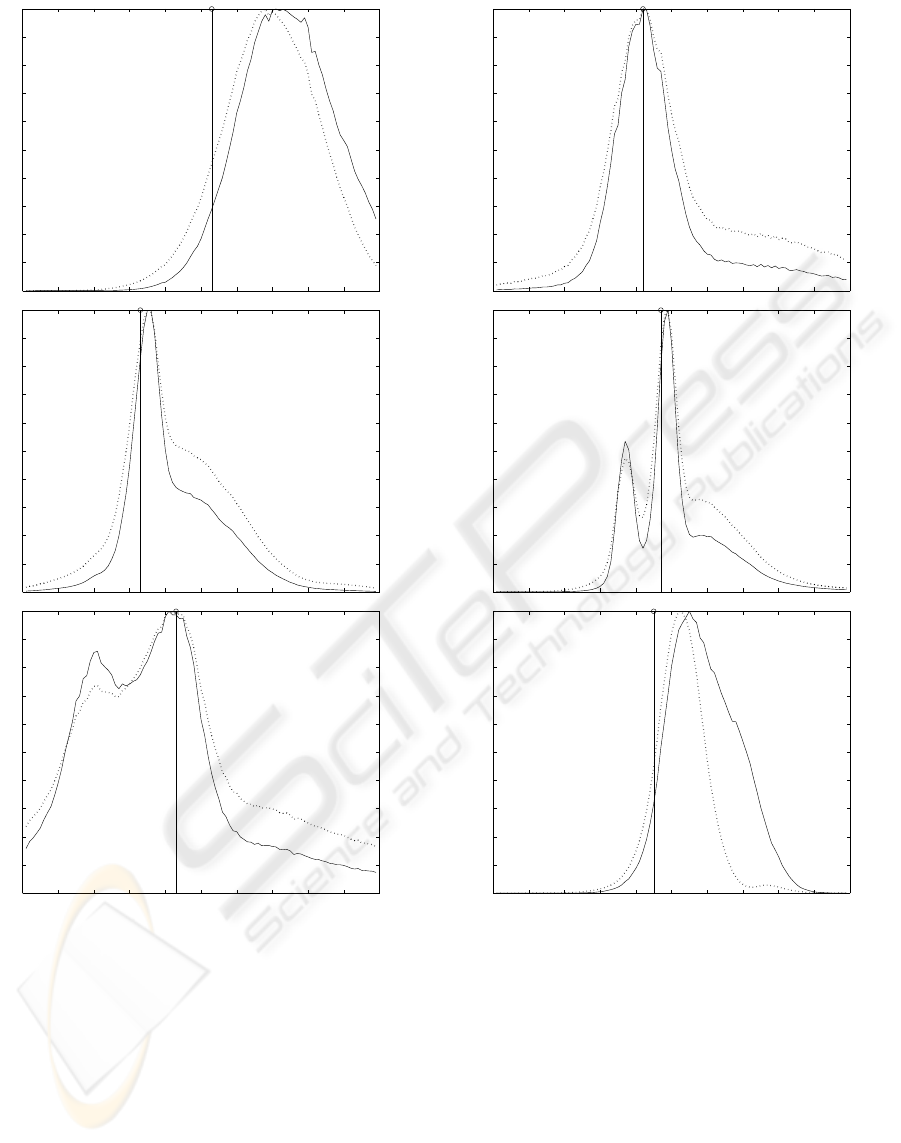
The graphs of the behaviour of this new focus

function on all six samples can be found in Figures

2 and 3.

Table 6: Comparison of focus positions found by Variance

and the genetic result.

Sample Reference Variance Genetic result

1 53 68 71

2 33 35 36

3 43 41 41

4 42 42 42

5 47 49 49

6 45 52 55

Total error – 28 35

Mean error – 4.6 5.8

5 CONCLUSION

In this work several different tasks were accom-

plished. Their unifying topic is the autofocusing for

automated microscopy that was simulated on a per-

sonal computer. First, 16 classic functions were tested

on biomedical data. None of them was as accurate and

reliable as would be necessary. Nevertheless, some

of them are usable, mainly Variance and Vollath’s F5.

Second, Boddeke’s algorithm was tested. It turned out

that the algorithm can be modiﬁed so that it reliably

ﬁnds the maximum of the function despite the poten-

tial bimodality. Some 10 acquired images are needed

in average.

The weakest link is certainly the focus function it-

self. If this issue is solved, the automated focusing

can become routine work without the need of human

assistance. In order to ﬁnd such a function, a pre-

liminary genetic programming experiment was con-

ducted. Its result is comparable to the Variance. This

genetic programming application has shown the im-

portance of solving the strong typing issue. An algo-

rithm for tree generation using a variant of strongly

typed genetic programming was designed, and an im-

portant property – the type-consistence – of elemen-

tary functions was recognized and deﬁned.

5.1 Future Work

The genetic programming design could be improved

by more careful selection of elementary functions, pa-

rameters etc. Running the program parallelly could

enable using more individuals, generations and train-

ing samples. This altogether could result in a highly

TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED MICROSCOPY

445

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 2: Genetic result (solid line) and Variance (dotted

line) on testing samples 1 to 3 from top to bottom. The

reference value is highlighted.

ﬁt focus function of unprecedented performance that

would discover the hidden features of images in fo-

cus. Finally, the results from PC simulations could be

realized on a real automated microscope.

ACKNOWLEDGEMENTS

This work was supported by the Ministry of Edu-

cation of the Czech Republic (Grants No. MSM-

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 3: Genetic result (solid line) and Variance (dotted

line) on testing samples 4 to 6 from top to bottom. The

reference value is highlighted.

0021622419, No. LC535 and No. 2B06052).

REFERENCES

Boddeke, F. R. (1999). Quantitative Fluorescence Mi-

croscopy. PhD thesis, Technische Universiteit Delft.

Boddeke, F. R., van Vliet, L. J., Netten, H., and Young, I. T.

(1994). Autofocusing in microscopy based on the otf

and sampling. Bioimaging, 2:193–203.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

446

Bueno-Ibarra, M. A.,

Alvarez Borrego, J., Acho, L., and

avez-S

anchez, M. C. (2005). Fast autofocus algo-

rithm for automated microscopes. Optical Engineer-

ing, 44.

Firestone, L., Cook, K., Culp, K., Talsania, N., and Preston,

K. (1991). Comparison of autofocus methods for au-

tomated microscopy. Cytometry, 12:195–206.

Geusebroek, J., Cornelissen, F., Smeulders, A., and Geerts,

H. (2000). Robust autofocusing in microscopy. Cy-

tometry, 39:1–9.

Groen, F. C., Young, I. T., and Ligthart, G. (1985). A com-

parison of different focus functions for use in autofo-

cus algorithms. Cytometry, 6:81–91.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press.

Kozubek, M., Kozubek, S., Luk

sov

a, E., Mare

ckov

a, A.,

artov

a, E., Skaln

ıkov

a, M., and Jergov

a, A. (1999).

High-resolution cytometry of ﬁsh dots in interphase

cell nuclei. Cytometry, 36:279–293.

Mitchell, M. (1996). An Introduction to Genetic Algo-

rithms. Massachusetts Institute of Technology.

Montana, D. J. (1995). Strongly typed genetic program-

ming. Evolutionary Computation, 3:199–230.

Netten, H. (1997). Automated Image Analysis of FISH-

Stained Cell Nuclei. PhD thesis, Delft University of

Technology.

Santos, A., Ortiz de Sol

orzano, C., Vaquero, J. J., Pe

na,

J. M., Malpica, N., and del Pozo, F. (1997). Evalu-

ation of autofocus functions in molecular cytogenetic

analysis. Journal of Microscopy, 188:264–272.

Silva, S. and Almeida, J. (2003a). Dynamic maximum tree

depth - a simple technique for avoiding bloat in tree-

based gp. In Proceedings of the Genetic and Evolu-

tionary Computation Conference (GECCO-2003).

Silva, S. and Almeida, J. (2003b). Gplab - a genetic pro-

gramming toolbox for matlab. In Proceedings of

the Nordic MATLAB Conference (NMC-2003), pages

273–278.

Sun, Y., Duthaler, S., and Nelson, B. J. (2004). Autofocus-

ing in computer microscopy: Selecting the optimal fo-

cus algorithm. Microscopy Research and Technique,

65:139–149.

APPENDIX

I(x, y, z) ...The intensity of a pixel at a position (x, y)

in an image I acquired at the z-position z

m, n .. .The width and height of an image I

I(z) ...The average of the pixel intensity of an image

I acquired at the z-position z, i. e.,

∑

I(x,y,z)

m·n

h(i) ...Number of pixels of intensity equal to i in I

p(i) ... The frequency of occurrence of pixels with

intensity equal to i in an image I, i. e., p(i) =

h(i)

The list of the focus functions tested:

1. Absolute Gradient

f(z) =

∑

|I(x, y, z) − I(x, y− 1, z)|

2. Square gradient

f(z) =

∑

(I(x, y, z) − I(x, y− 1, z))

3. Netten’s ﬁlter

f(z) =

∑

(I(x+ 1, y, z) − I(x− 1, y, z))

4. Energy Laplace

f(z) =

∑

C(x, y,z)

where C(z) = I(z) ∗



−1 −4 −1

−4 20 −4

−1 −4 −1



5. Laplacian

f(z) =

∑

(I(x, y− 1, z) − 2I(x, y, z) + I(x, y+ 1, z))

6. Tenegrad’s function

f(z) =

∑

(x, y, z)

+ S

(x, y, z)

where

(z) = I(z)∗



1 2 1

0 0 0

−1 −2 −1



, S

(z) = I(z)∗



−1 0 1

−2 0 2

−1 0 1



7. Signal Power

f(z) =

∑

(I(x, y, z)

8. Variance

f(z) =

∑

(I(x, y, z) −

I(z))

9. Normalized Variance

f(z) =

mn(I(z))

∑

(I(x, y, z) −

I(z))

10. Absolute Variance

f(z) =

∑

|(I(x, y,z) −

I(z)|)

11. Normalized Absolute Variance

f(z) =

mn(I(z))

∑

|(I(x, y,z) − I(z)|)

12. Histogram Range

f(z) = max

(h(i) > 0) − min

(h(i) > 0)

13. Histogram Entropy

f(z) = −

∑

· log

14. Vollath’s F

f(z) =

∑

I(x, y, z) · I(x+ 1, y, z)−

−

∑

I(x, y, z) · I(x+ 2, y, z)

15. Vollath’s F

f(z) =

∑

I(x, y, z) · I(x+ 1, y, z) − mn(

I(z))

16. Spectral Analysis

f(z) =

∑

· log

TOWARDS RELIABLE AUTOFOCUSING IN AUTOMATED MICROSCOPY

447