DYNAMIC REAL-TIME REDUCTION OF MAPPED FEATURES IN A

3D POINT CLOUD

Marko Reimer and Bernardo Wagner

Institute for Systems Engineering, Leibniz University Hanover, Hanover, Germany

Keywords:

3D perception, real-time processing, data reduction.

Abstract:

This paper presents a method to reduce the data collected by a 3D laser range sensor. The complete point

cloud consisting of several thousand points is hard to process on-line and in real-time on a robot. Similar

to navigation tasks, the reduction of these points to a meaningful set is needed for further processes of object

recognition. This method combines the data from a 3D laser sensor with an existing 2D map in order to reduce

mapped feature points from the raw data. The main problem is the computational complexity of considering

the different noise sources. The functionality of our approach is demonstrated by experiments for on-line

reduction of the 3D data in indoor and outdoor environments.

1 INTRODUCTION

Environmental perception of mobile robots is still a

challenging task. Many research groups work on im-

provements for on-line spatial perception. Almost all

possible kinds of sensors are used to collect informa-

tion. Actually, lots of research in robotics deals with

the localization and mapping problem. Partly, this re-

search is based on features. These features are mostly

lines, planes or special edges. Few research is done in

processing all the raw data in real-time on the robot

itself. The main problem for doing it on-line is the

less time for each process combined with less com-

putation power for each step to ﬁnish. A further ﬁeld

of research, mainly in security context, focuses on ob-

ject detection. On-line algorithms for object detection

must be integrated into the control process to be of

any advantage for robot task fulﬁllment and have to be

ﬁnished in real-time time. One of the most important

steps to speed up the data processing is to reduce the

collected data to a meaningful set of data. An exam-

ple for this is the mapping and localization problem.

Therefore feature points in 3D are extracted, mapped

into a 2D map and well known 2D algorithms are ap-

plied (Wulf et al., 2004b). The intention of this paper

is to present a way to reduce the amount of data col-

lected by a 3D range scanner for a following on-line

object detection. This reduction uses environmental

context knowledge to remove static features like walls

from the 3D point cloud and keep only information

not present in the given map. This may be used for re-

ducing speed of an autonomous vehicle within range

of dynamic obstacles. The reduceable feature points

are found by two criteria. First, several sequent points

must form a vertical line in 3D space. Second, this

line must be matched to the environment map of the

robot. As the computation power and the data stor-

age for on-line reduction is limited, only actual data

is used without keeping any previous information or

calculating averages over time.

Another beneﬁt reducing the raw data, additional

to the gain in speed, is the better result of algorithms

working on the reduced data set. A following ob-

ject detection and segmentation algorithm may not be

confused by mapped (known) features any more. For

an example segmentation see (Talukder et al., 2002).

The main problem handled in this paper is match-

ing the 3D-data in the presence of different kinds of

noise. All used sensors and maps have different forms

of noise requiring different handling.

The paper is organized in 5 parts. The remaining

part of section 1 describes the form of the input data.

Section 2 describes similar work. Section 3 shows

the steps needed for the reduction and ways to handle

363

Reimer M. and Wagner B. (2007).

DYNAMIC REAL-TIME REDUCTION OF MAPPED FEATURES IN A 3D POINT CLOUD.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 363-369

DOI: 10.5220/0001638003630369

 SciTePress

uncertainties. After that, the experiments carried out

on two robot platforms one indoor and one outdoor

are shown in section 4. The conclusion is drawn in

the 5. section.

The 3D data to be reduced is measured from a

continuous 360 degree 3D laser range scanner. To be

able to collect data while moving a movement com-

pensation is applied. For details on the 3D sensor and

the movement compensation see (Wulf and Wagner,

2003) or (Reimer et al., 2005). A 3D scan is organized

as an ordered sequence of vertical 2D laser scans (see

Figure 1 left) in clockwise rotating directions. One set

of 3D data always contains a 360 degree turn of the

3D scanner. Each 2D laser scan itself is an ordered

list of points in 3D space. There is a ﬁxed number of

points per 2D scan which are ordered from bottom di-

rection towards ceiling direction. The points are given

in cartesian coordinates with the origin centered at the

laser scanner.

Like a normal 2D map the map used for reduction

represents the environment in a top view. The map

consists of a set of lines deﬁning surfaces detectable

by a range sensor (see Figure 1). As the map is de-

signed and also used for localization it only needs to

include a 2D representation of the environment. This

kind of map is often build from landmark ofﬁces or

construction plans, which are not including 3D infor-

mation. It might be build from aerial images given

ground truth.

Figure 1: Left: Schematic of a 2D/3D Scan; Right: Sample

map of our ofﬁce environment.

2 RELATED WORK

At the ﬁrst step, each 2D scan is handled seperately.

Each 2D scan is segmented into lines. These line

features extracted from range data are used by sev-

eral successful systems as they are easy to compute

and quite compact to handle. There are several pa-

pers how to construct line features. Two of the most

commonly used ways are either Hough transforma-

tion (Pﬁster, 2003), and the split-and-merge approach

(Borges, 2000). For an overview of line segmentation

algorithms see (Nguyen et al., 2005).

The closest work to ours is the work extracting

walls from 3D points collected by a static mounted

but moved 2D scanner. For example (Thrun, 2003)

collect these data with a helicopter, and Haehnel et al.

do so with a moving robot (Haehnel et al., 2003). The

main difference is the way 3D points are built. In their

case the whole system is moved along a given path

while the sensor is static on the system. They achieve

a more dense point cloud and have a reduced angular

error. They do not reduce the data on-line and in real-

time but they post process the whole point cloud to

extract matched walls using the EM-algorithm.

The proposed method should remove as much

points as possible of visible matching feature parts.

In contrast to the shown wall matching methods with

a minimum 2D size, our method needs only a line to

be detectable. The overall height of a line or plane is

not constrainted. The removed features are not con-

stricted by any minimum size requirement as it de-

pends on the distance to the feature.

Another similar technique is the well researched

segmentation of horizontal 2D range data into line

features and matching them with a given 2D map.

This is mostly done for localization like (Biber, 2005)

and (Pﬁster, 2003). This is at least done on-line

while the system operates. In the case of a vertical

mounted 2D scanner vertical and not horizontal lines

are measured, which differ in handling. Horizontal

line matching has to deal with similar sensor noise

and errors in the position estimation. But the horizon-

tal neighborship of succeeding points can be used to

account for the angular error in the localization. Com-

pared to a horizontal neighbouring point a whole line

in the vertical scan is effected by this error. The line

cannot be corrected by weighting the single point with

neighboring points into a line.

On the ﬁrst sight, the well researched area of map-

ping is very similar to the described problem. There

is an enormous number of papers about ‘SLAM’

which are at least partly dealing with the problem of

mapping ((Thrun et al., 2005), (Thrun et al., 2004),

(Nuechter et al., 2005), (Kuipers and Byun, 1990)).

Especially the survey (Thrun, 2002) gives a good

overview. The main difference of our approach to

the mapping problem is that we assume to know our

position and orientation up to a remaining error in-

troduced by the localization. It is not our attempt to

improve the quality of the localization in any kind

as we want to detect and segment dynamic objects.

The SLAM takes a big advantage of the possibility

to sense a particular point in space twice or more of-

ten. As shown in (Thrun, 2002) they take an EM-

algorithm to maximize the probability of a particular

cell in a grid map. This is manly done using multiple

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

364

views of the same cell over time. We want to reduce

data immediately. These SLAM algorithms include

methods for an estimated match of 2D point positions,

mostly positions of feature points, with a given 2D

map of the environment for localization (Wulf et al.,

2004a).

Another similar topic is the iterative matching of

two 3D scans or the iterative matching of features to

3D scans. There exist lots of matching techniques.

The most popular technique is the iterative closest

point (ICP) algorithm based on (Besl and McKay.,

1992). As all these techniques try to give an optimal

result in the overall match it takes too much computa-

tion time for our application.

3 REAL-TIME REDUCTION OF

3D DATA

Assuming a perfect localization, a perfect map and a

noiseless sensor, the mathematical model for the re-

duction of 3D data to a 2D-map is straightforward. If

the sensor is located at position α and the measured

points form an exact vertical line at position β both

positions can be transformed into positions within the

map without any error. The position of the robot in

the map is ι and the feature position is called δ. It is

a comparison between the measured distance and the

distance given by the map assuming the same direc-

tion.

αβ

− d

ιδ

= ζ (1)

If ζ is smaller than a threshold, the points are re-

moved.

3.1 Laser Scanner Noise

The most common problem is the measurement noise

of the laser range sensor. We show here how to care

about the sensor noise without explizitly handling ev-

ery point but combining the errors into a line repre-

sentation. Range sensors mostly report data in a po-

lar representation consisting of a distance measure-

ment and a corresponding measurement angle. The

distance measurement of commonly used laser scan-

ners underlies a gaussian noise as shown in (Ye and

Borenstein, 2002). This noise depends on parame-

ter as temperature, incidence angle and color of the

scanned surface. They showed that the inﬂuence of

the surface properties is less than the inﬂuence of the

incidence angle. As for example in (Pﬁster, 2002) the

noise of a 2D laser scanner in the measured angle can

be modeled as an additive zero-mean gaussian noise

with a variance of σ

. Whereas a common assumption

is less than one degree. The resulting measured

distance vector

meas

is calculated by

meas

= (d

true

+ ε

sensor

) ×



cos(Θ+ ε

)

sin(Θ+ ε

)



(2)

with Θ being the assumed angle of the measure-

ment and ε being the corresponding error. For our

reduction we do not consider single points and their

noise but lines. These lines allow us to handle the

sensor noise as an distance interval in the 2D ground

distance d

ground

meas

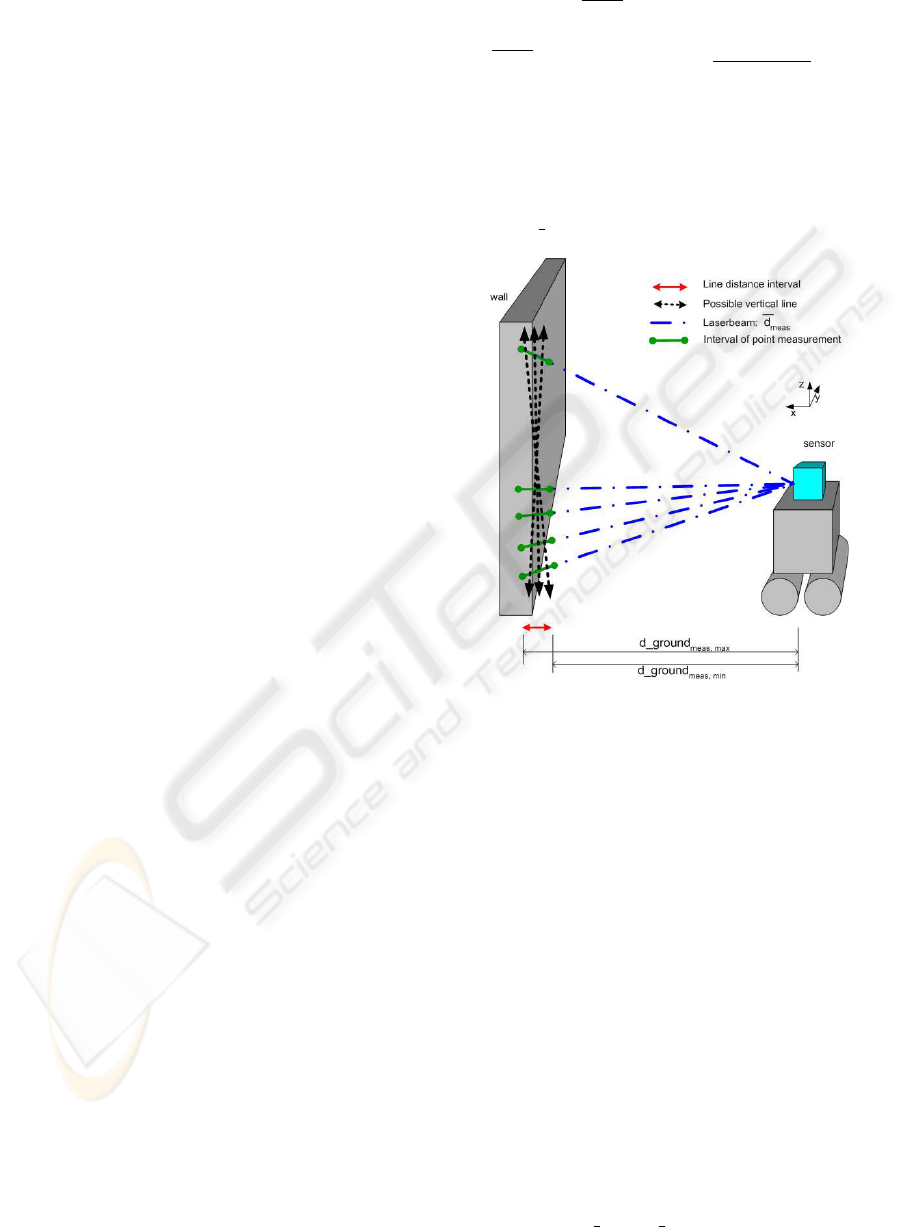
Figure 2: Sensor noise - points forming lines.

Figure 2 shows an example of the possible distri-

butions of some wall points. As all points are taken

on the front side of the wall they must be measured

at the real distance added gaussian noise. The pos-

sible locations of the scanned points are shown by

the intervals around the true front point at the wall

(green solid lines). The line search algorithm is con-

ﬁgured to some maximum distance a measured point

may have towards the line. This deﬁnes the spread

of points around the line. After ﬁtting a line through

the points the upper and the lower end point of the

line deﬁne the maximum and minimum distance of

the line to the sensor. There are several orientation

possibilities for the found line, depending on the dis-

tribution of the noise (dotted orange lines). The angle

of the found line against the z-axis is named γ. It’s

bound by a userdeﬁned treshold η. This line forms

the measured ground distance interval at the xy-plane

(red line). This interval is given by:

ground line

meas, j

= (3)

DYNAMIC REAL-TIME REDUCTION OF MAPPED FEATURES IN A 3D POINT CLOUD

365

[min

(d ground

meas,i

);max

(d ground

meas,i

)]

with i all points forming line j.

The mounting of the scanner does not need to be

exactly vertical. So an error in the orientation of the

lines is introduced. This angular difference is directly

visible in the orientation of the measured line (orange

line in Figure 2. All lines are not exactly vertical any-

more but tilted. The tilting angle adds to the interval

of possible line orientation angles (γ). This angular

error results in different distances for the upper and

lower ending of the line. The error in the distance is

dependent on the length or height of the wall and the

height of the scanner position. This error has a maxi-

mum inﬂuence, if both ends of the line strongly differ

in the height towards the sensor. As an example a 2

degree mounting error results in a 10 cm distance er-

ror, if the line has a height of 3 m, if the scanner is

mounted on the ground. This distance difference adds

to the distance interval caused by the sensor distance

noise.

error

(γ) = height ∗ tan(γ) (4)

As the tilting of the sensor is detectable during the

mounting process it can be mechanically bound. To

simpliﬁy calculations this maximum bound is used.

The minimum distance is given by:

total

meas,min

= d ground line

meas,min

− d

error

(γ)

(5)

Similar calculations can be applied for the maximum

distance. Together these two values form the mea-

sured distance interval.

3.2 Localization Distance Noise

For calculating the expected distance the map and the

output of the localization are used. These values are

independent of the sensor model. As our algorithm

relies on a given localization, we must take the error

of the localization into account. A commonly used

model for the localization error (Thrun et al., 2005)

describes the located position as an ellipse with axis

a and b, the orientation as an angle ω added a zero-

mean gaussian noise ε

. There is no general bound on

the localization error which can be applied to all dif-

ferent kinds of localization methods. So we assume

these variances to be known for each position. As

we want to reduce data very fast, we do not try to

upgrade the position data by any means. We use the

radii of the ellipses to calculate the possible difference

in the ground distance introduced by the localization

and build an interval of this size around the reference

value taken from the map using the center of the el-

lipse.

position

1− a

cos

(κ)

(6)

κ is the direction of the scan. It is counted clockwise

from the front direction of the scanner.

Figure 3: Localization position error.

The condition for the reduction is given by equa-

tion 7, when the angular error of the localization is

not considered.

map

− r

position

≤ d total

meas,min

≤ d

map

+ r

position

)

or (7)

map

− r

position

≤ d

total

meas,max

≤ d

map

+ r

position

)

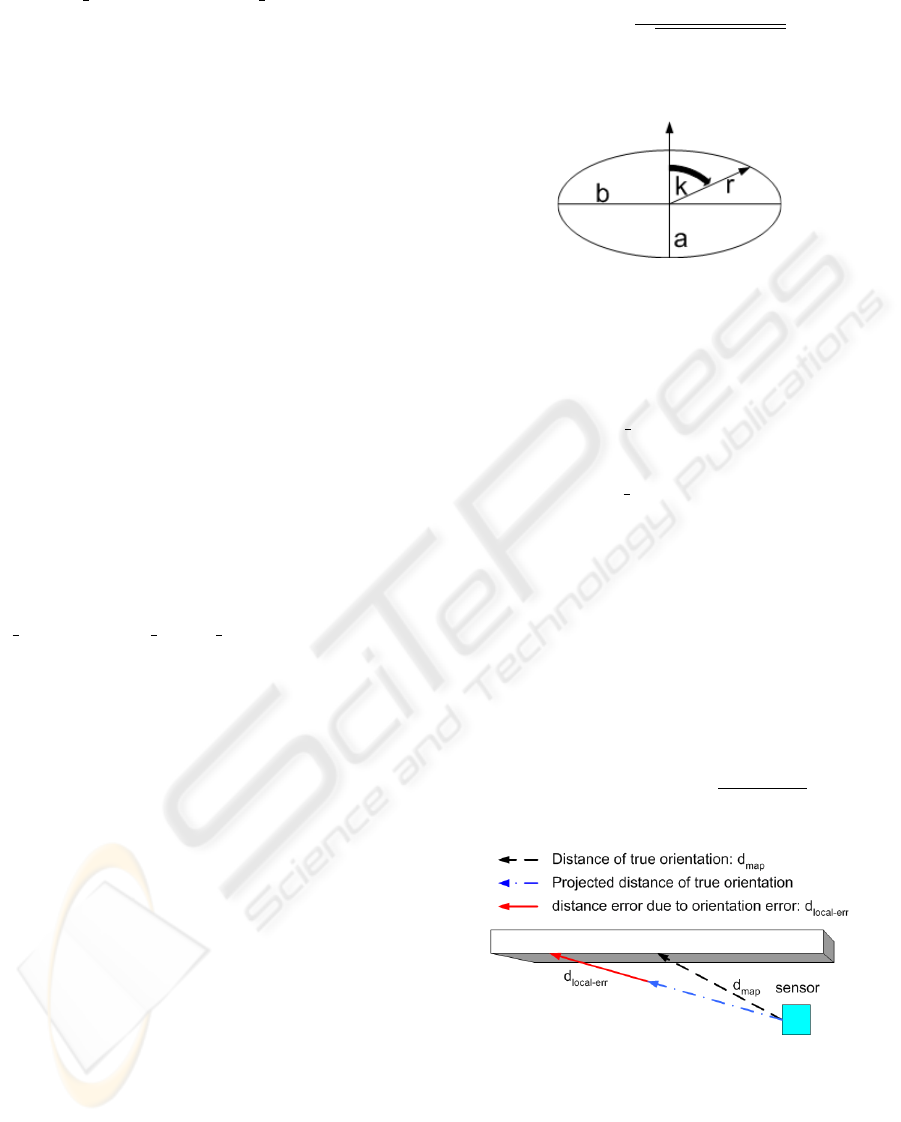
3.3 Localization Orientation Noise

The angular difference between the true orientation

and the measured orientation has a worse effect than

the position error. On a plane object or wall this angu-

lar error introduces a difference in the incidence angle

ρ between the beam and the object. The resulting er-

ror in the distance is dependent on the distance and

the actual incident angle.

local−err

= d

map



1−

sin(ρ)

sin(ρ+ ε

)



(8)

Figure 4: Incidenceangle with orientation error.

This error might be of enormous impact for small

incident angles at large distances. If we add the dif-

ference d

local−err

(8) to the already calculated interval

by Section 3.2 it is no longer possible to distinguish

between objects signiﬁcant in front of the wall and

the wall itself. If we do not consider this error, the

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

366

points forming this line are not reduced and remain

for further processing steps. To account for this we

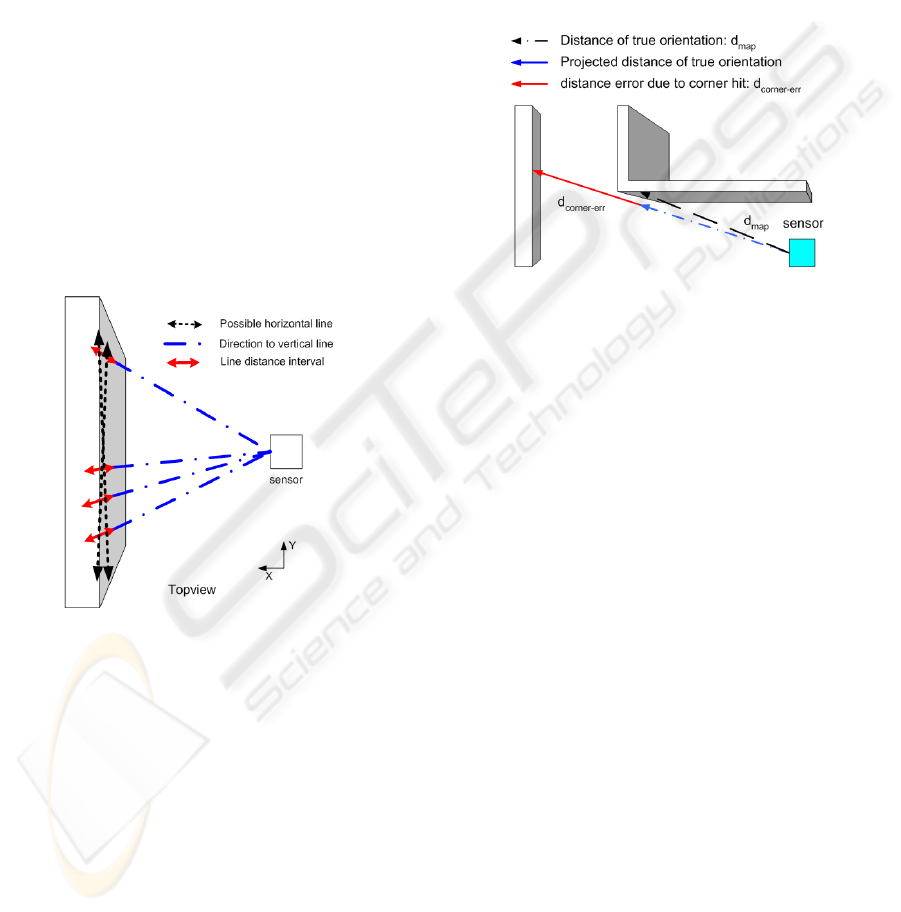
extend the identiﬁed lines from the measured points.

Our approach is to form a horizontal line from the al-

ready found vertical lines. The found vertical lines

are projected into the ground plane. They form an

interval or line in the xy-plane in contrast to the line

in the xyz-system in Figure 2. All already matched

wall lines are marked like the blue lines in Figure

5. The centers of neighboring matched ground lines

are tested for forming a horizontal line in the ground

plane using the same methode as in the ﬁrst part. The

next vertical line not already matched is tested to be a

part of this horizontal line. Doing this the difference

between the unmatched vertical line distance and the

horizontal line is bounded by the point distance dif-

ference and independent of the distance error between

the map and the measurement. If the vertical line in-

terval ﬁts into the horizontal line it is reduced as well.

This method needs the feature to be matchable at least

party. A matched segment must form a line to be ex-

tended.

Figure 5: Vertical lines forming horizontal line.

3.4 Remaining Noise Sources

The error in the estimation of the measurement angle

introduced by the servo drive cannot be handled in the

same way as the orientation error of the localization.

This error depends on the sampling frequency of the

servo drive position and it is acceleration. The posi-

tion of the servo drive is linear interpolated between

two measurements. If the servo drive accelerates the

change in turn velocity leads to an angular error de-

pendent on the acceleration speed and sampling fre-

quency of the position sensor. Both variables are con-

trollable by the user and may be chosen to result in

a negligible angular error. This might be reached, if

the system is considered to be turning with a constant

turn velocity after a startup phase.

The worst problem appears, if the angular differ-

ence between map and measured beam results in a hit

on a different object or wall due to a corner. In this

case the mathematical expression of the differences

in the distance are not longer valid. Partly, if the inci-

dence angle is small enough this case is caught by the

horizontal line extension. The lines not caught remain

as line in the point cloud.

Figure 6: Error hitting a corner.

The mixed pixel problem is not solved by our ap-

proach. A measured line of points within a mixed

pixel distance to the sensor cannot be matched to any

feature. As the remaining vertical lines are orphants

within their neighbourhood, they might be removed

in a postprocessing step.

Finally, the map itself is probably not perfect but

has some error. The error within the map is assumed

to be within the same dimension as the noise of the

range sensor. And therefore not handled explizit.

4 EXPERIMENTS

The proposed method has been implemented into the

perception module of our 3D laser scanner. This 3D

laser scanner is mounted on to two different chassis

one for indoor use Section 4.1 and one for outdoor use

Section 4.2. Both systems differ in various parameter

but use the same software environment. For the in-

door cases the map is created by hand using manually

measured length. The outdoor map is based on mate-

rial from the land registry ofﬁce. The map error is in

the dimension of centimeter. The same maps are used

for localization and reduction at all times. The 3D

laser scanner consists of a Pentium III Processor with

256 MB of RAM running a real-time linux (Xeno-

mai). The time needed for the reduction on this pro-

cessor is well below one second.

DYNAMIC REAL-TIME REDUCTION OF MAPPED FEATURES IN A 3D POINT CLOUD

367

4.1 Indoor Experiments

For the indoor experiment we were driving on the

ﬂoor with a speed of 0.5 m/s when the 3D scan has

been taken. Beside the walls and doors there is one

person and one cartoon standing on the ﬂoor roughly

in front of the robot. The doors on the left side are

closed, while the doors on the right are open. Through

the right door an ofﬁce is visible. This ofﬁce is

equiped with normal ﬁlled desks and cabinets at the

wall. On the back side a ﬁre extinguisher is located at

the wall.

Figure 7 shows all found vertical lines and the re-

sult of the reduction. The dark red lines have been

matched to the map while light green lines remain

unmatched. At a ﬁrst glance some lines within the

wall appear not vertical. This is a problem of the line

segmentation algorithm. As shown in (Borges, 2000)

the start and endpoints of a line are not always chosen

correctly. This may result in a wrong angle calculated

for that line. These single lines (the corresponding

points) will be removed after the matching step.

Figure 7: Reduced(red) and remaining lines(green) indoor.

On the left hand side all but one small vertical line

on the wall has been removed. The door in the front

part has not been modeled in the map and cannot be

reduced at all. (see Figure 1) Also the person and

the carton still remain as detected lines. The open

door on the right remains like the lines on the cabinets

within the ofﬁce. The wall on the right side is totally

removed even far in front at small incidence angles.

This is due to the applied wall extension. The far wall

on the left side cannot be removed because the person

is totaly blocking the wall extension. On the back side

on the left, between Scanindex 0-1, some lines which

belong to a wall have not been removed. This is due to

the error in the orientation while processing a corner

in the map. At this direction no wall is found. The

calculated beam hits the right side of the corner with

the front wall, while the measured beam passes on the

left side to the about 5m far away wall. The small

line not removed around scanIndex 22 belongs to an

other open door. In total from 12300 points forming

vertical lines about 11700 points are removed. The

complete 3D scan has 32761 points.

4.2 Outdoor Experiments

For the outdoor experiments we drove around a park-

ing lot with several warehouses around. These build-

ings form the vertical lines to be matched. All existing

features have been found as lines. As the distance to

the buildings is big compared to the indoor distances

much less points form vertical lines. All found ver-

tical lines are shown in Figure 8. The removed ver-

tical lines are dark red and remaining vertical lines

are light green. These remaining lines are mostly lo-

cated at the wirefence on the right side and the bush

on the front side. Both are not represented in the map

to be removed. The white area shows points not iden-

tiﬁed as vertical line and so not applictable for our

reduction. All existing features have been removed

while all dynamic objects are remaining. The com-

putational complexity of further steps is reduced by

more than 50 percent as most of the signiﬁcant points

are removed.

Figure 8: Reduced (dark red) and remaining lines (light

green) outdoor.

5 CONCLUSION

In this paper we presented a method for real-time and

on-line reduction of a 3D point cloud by given rough

2D-environmental knowledge. The method ﬁnds ver-

tical line features in the 3D data and matches them

to a given 2D map of these features. The problem

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

368

for this procedure is the different noise introduced by

several measurements. In order to speed up the calcu-

lation and simpliﬁy to noise handling we do not deal

with every single point but build higher level line fea-

tures. These line features are suitable to incorporate

the noise added to the distance measurements. The

line approach is used a second time on the line fea-

tures itself, in order to handle the error in the orien-

tation angle. The vertical lines are reduced to points

on the ground which form a horizontal line feature to

be independent of the relative orientation. A possible

extension could be the integration of a non straight

feature model as for example curved walls.

The proposed method is well suited for dynamic

and complex environments as long as a simple 2D-

map of matchable features is given and these features

remain visible beside the dynamic objects. It im-

proves a following object detection and recognition

in computational speed and result quality.

The best improvement for the reduction quality

may be gained by an improvement of the localization.

Until the localization error is in the same dimension

as the sensor noise, the use of a second or better sen-

sor is not usefull. A possible extension might be to

use the intensity value delivered by a range sensor to-

gether with the distance value. This intensity value

is proportional to the strength of the reﬂection of the

transmitted signal. The uncertainty interval of a mea-

sured distance could be calculated corresponding to

the measured intensity of the distance. But the in-

tensity is dependent on many factors not only on the

incident angle and the other inﬂuences have to be can-

celed out before.

REFERENCES

Besl, P. J. and McKay., N. D. (1992). A method for

registration of 3-d shapes. IEEE Trans. on PAMI,

14(2):239256.

Biber, P. (2005). 3d modeling of indoor environments for

a robotic security guard. Proceedings of the 2005

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition (CVPR05).

Borges, G.A; Aldon, M.-J. (2000). A split-and-merge seg-

mentation algorithm for line extraction in 2d range im-

ages. Pattern Recognition, 2000. Proceedings. 15th

International Conference on, pages 441–444.

Haehnel, D., Triebel, R., Burgard, W., and Thrun, S. (2003).

Map building with mobile robots in dynamic environ-

ments. ICRA.

Kuipers, B. and Byun, Y.-T. (1990). A robot exploration

and mapping strategy based on a semantic hierarchy

of spatial representations. Technical Report AI90-120.

Nguyen, V., Martinelli, A., Tomatis, N., and Siegwart, R.

(2005). A comparison of line extraction algorithms

using 2d laser rangeﬁnder for indoor mobile robotics.

International Conference on Intelligent Robots and

Systems, IROS2005,.

Nuechter, A., Lingemann, K., Hertzberg, J., and Surmann,

H. (2005). 6D SLAM with approximate data associa-

tion. ICRA.

Pﬁster (2002). Weighted range sensor matching algorithms

for mobile robot displacement estimation. Interna-

tional Conference on robotics and automation, pages

1667–1675.

Pﬁster, Samuel; S. Rourmelitis, J. B. (2003). Weighted line

ﬁtting algorithms for mobile robot map building and

efﬁcient data representation. International conference

on robotics and automation, pages 1304–1312.

Reimer, M., Wulf, O., and Wagner, B. (2005). Continuos

360 degree real-time 3d laser scanner. 1. Range Imag-

ing Day.

Talukder, A., Manduchi, R., Rankin, A., , and Matthies,

L. (2002). Fast and relaiable obstacle detection and

segmentation for cross-country navigation. Intelligent

Vehicle Symposium, Versaille, France.

Thrun, S. (2002). robotic mapping a survey. Book chap-

ter from ”Exploring Artiﬁcial Intelligence in the New

Millenium”.

Thrun, S. (2003). Scan alignment and 3-d surface modeling

with a helicopter platform. IC on Field and service

robotics, 4th.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

Robotics. The MIT Press.

Thrun, S., Montemerlo, M., Koller, D., Wegbreit, B., Ni-

eto, J., and Nebot, E. (2004). Fastslam: An efﬁcient

solution to the simultaneous localization and mapping

problem with unknown data association. Journal of

Machine Learning Research.

Wulf, O., Arras, K. O., Christensen, H. I., and Wagner, B.

(2004a). 2d mapping of cluttered indoor environments

by means of 3d perception. ICRA.

Wulf, O., Brenneke, C., and Wagner, B. (2004b). Col-

ored 2d maps for robot navigation with 3d sensor data.

IROS.

Wulf, O. and Wagner, B. (2003). Fast 3d scanning methods

for laser measurement systems. International Con-

ference on Control Systems and Computer Science

(CSCS), 1.

Ye, C. and Borenstein, J. (2002). Characterization of a

2-d laser scanner for mobile robot obstacle negotia-

tion. International Conference on Robotics and Au-

tomation.

DYNAMIC REAL-TIME REDUCTION OF MAPPED FEATURES IN A 3D POINT CLOUD

369