SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME

DELAYS FOR WATER-ASSET MANAGEMENT OF NETWORKED

OPEN-CHANNEL SYSTEMS

Eric Duviella

Ecole des Mines de Douai, Dpt. Informatique et Automatique, 941 rue Charles Bourseul, 59508 Douai, France

Pascale Chiron and Philippe Charbonnaud

Laboratoire G

enie de Production, Ecole Nationale d’Ing

enieurs de Tarbes, 47 av. d’Azereix, 65016 Tarbes, France

Keywords:

Supervision, hybrid control accommodation, resource allocation, setpoint assignment, networked systems,

water management.

Abstract:

The paper presents a new strategy based on a supervision and hybrid control accommodation to improve the

water-asset management of networked open-channel systems. This strategy requires a modelling method of

the network based on a weighted digraph of instrumented points, and the deﬁnition of resource allocation

and setpoint assignment rules. Two setpoint assignment rules are designed and evaluated in the case of an

open-channel system composed of one diﬂuent and one conﬂuent showing their effectiveness.

1 INTRODUCTION

A hydrographic network is a geographically dis-

tributed system composed of dams and interconnected

rivers and channels. Weather conditions and hu-

man activities have a great inﬂuence on the ﬂow dis-

charges. An interesting problem to address deals with

the allocation of water quantities in excess toward

the catchment area and of water quantities in lack

amongst the users. The complex hydrographic net-

work representation, as well as the determination of

the discharge allocation on the network, constitute an

essential step for the design of reactive control strate-

gies. In (Naidu et al., 1997) a hydrographic network

representation by oriented graphs is proposed by con-

sidering only the diﬂuences. This representation is

modiﬁed and extended to the cases of the conﬂu-

ences in (Islam et al., 2005). Cembrano et al (Cem-

brano et al., 2000) proposed a modelling approach for

the drinking water distribution networks, and sewer-

age networks. Object-oriented modelling techniques

(Chan et al., 1999) and a XML approach (Lisounkin

et al., 2004) allow the representation of the control

and measurement instrumentation equipping the hy-

drographic networks and the drinking water distribu-

tion networks. Optimization techniques were pro-

posed in the literature for the water-asset manage-

ment. The approach proposed in (Faye et al., 1998) al-

lows the adjustment of the criteria and the constraints

of an optimization problem starting from the supervi-

sion of the network variables. However, the complex-

ity of the hydrographic networks and the number of

instrumented points to be taken into account in the op-

timization problem require the use of decomposition

and coordination techniques of the studied systems as

proposed in (Mansour et al., 1998). These techniques

are used for the optimal water management of irriga-

tion networks. Finally, in (Duviella et al., 2007), a

supervision and hybrid control accommodation strat-

egy is proposed for the water asset management of

the Neste canal in the southwestern region in France.

This strategy can be adapted for the case of gridded

hydrographic networks.

In this paper, the allocation and setpoint assign-

ment rules are proposed for the water asset manage-

ment of complex hydraulic systems i.e. with conﬂu-

ences and diﬂuences. Networked hydraulic systems

modelling is presented in section 2. In section 3, iden-

tiﬁcation steps of transfer time delay are presented.

The supervision and resource allocation rules are pro-

posed in section 4. Section 5 deals with the design

of a water asset management strategy where two set-

point assignment rules are compared. Finally, their

evaluation by simulation within the framework of a

hydrographic system is carried out.

312

Duviella E., Chiron P. and Charbonnaud P. (2007).

SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME DELAYS FOR WATER-ASSET MANAGEMENT OF NETWORKED OPEN-CHANNEL

SYSTEMS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 312-319

DOI: 10.5220/0001637803120319

 SciTePress

2 NETWORKED HYDRAULIC

SYSTEM MODELLING

Hydrographic networks are composed of a ﬁnite num-

ber of Simple Hydraulic Systems (HYS), i.e. com-

posed of one stream. A HYS source is deﬁned as a

HYS which is not supplied by others HYS. A rep-

resentation is proposed to locate the instrumentation,

i.e. the sensors and the actuators, and to be able to

determine the way to distribute a water quantity mea-

sured in a place of the hydrographic network, onto the

whole HYS downstream. HYS are indexed by an in-

dex b, and all these indices forms the set B ⊂ N. Each

HYS is equipped with several sensors M

and actua-

tors G

, with i ∈ [1, m] and j ∈ [1,n], where m and

n are respectively the total number of measurement

points and actuators, as shown in Figure 1.a. Up-

per indexes are omitted when not necessary for com-

putation and comprehension. The structure of a hy-

drographic network is described by distinguishing the

conﬂuences (see Figure 1.a) and the diﬂuences (see

Figure 1.c).

Figure 1: (a) A conﬂuence, (c) its associated weighted di-

graph, (b) a diﬂuence, (d) its associated weighted digraph.

According to the hydraulic conditions and the

equations of energy and mass conservation, the sum

of the discharges entering a node (conﬂuent or diﬂu-

ent), is equal to the sum of the discharges outgoing

from this node. Thus, around an operating point, the

discharge q

of the HYS b resulting from the con-

ﬂuence between several HYS is equal to the sum of

the upstream HYS discharges, q

∑

r∈C

, where C

⊂ B is the set of the HYS indices upstream to the

HYS b. In addition, the HYS r resulting from the

diﬂuence of the HYS b upstream is supplied with a

proportion w

such that the discharge q

veriﬁes the

relation: q

= w

. In order to represent diﬂuence,

each HYS of an hydrographic system is associated to

a discharge proportion w

. For the HYS source and

Table 1: Assignment function of R matrix.

Input: weighted digraph.

Output: proportion matrix R.

Initialization of R to 0

For each node h

If h is a measurement point

Run (h, h, 1,R)

EndIf

EndFor

Run (h, c, p, R),

For each successor d of c

← p.w

Run (h, d, p

, R),

If d is a gate

R(h,d) ← R(h,d) + p

EndIf

EndFor

for the HYS downstream from a conﬂuence (see Fig-

ure 1.a) it is equal to 1. The discharge proportion w

of the HYS downstream the HYS b are known and

such as ∀r ∈ D

, w

< 1, and

∑

r∈D

= 1, where D

⊂ B is the set of HYS indices resulting from the di-

ﬂuence of the HYS b (see Figure 1.b). A discharge

which is measured in a place of the hydrographic net-

work, supplies the HYS downstream with discharge

proportions according to the structure of the hydro-

graphic network.

The hydrographic systems are represented by a

weighted digraph of instrumented points in order

to determine the discharge proportions between two

places of the networks. The digraph is composed

with a succession of two types of nodes M

or G

represented respectively by full circle and circle and

their respective graphs, and arcs indicate the links be-

tween the successive nodes (see Figure 1.c and Fig-

ure 1.d). The arcs are oriented in the direction of

the ﬂow and are weighted by the discharge propor-

tion between the two nodes w

. Thereafter, an algo-

rithm lead to the generation of the proportion matrix

R which is composed of m lines (measurement points)

and of n columns (actuators). The weighted digraph

is browsed for each measurement point M

following

the algorithm given in Table 1. The matrix R contains

all the discharge proportions of a point to another of

the hydrographic networks.

Thereafter, the transfer time delay between the

measurement points and the gates, is computed ac-

cording to the method described in the next section.

SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME DELAYS FOR WATER-ASSET MANAGEMENT

OF NETWORKED OPEN-CHANNEL SYSTEMS

313

3 IDENTIFICATION OF

TRANSFER TIME DELAYS

Hydrographic systems consist of several reaches, i.e.

a part between two measurement points, each reach

being composed of Open-Channel Reach Section

(OCRS), i.e. a part between two gates, between a

measurement point and a gate or between a gate and

a measurement point. The OCRS dynamics can be

modelled by transfer functions according to the mod-

elling method which consists in the simpliﬁcation

of the Saint Venant equations and their linearization

around an operating point (Litrico and Georges, 1999;

Malaterre and Baume, 1998; Chow et al., 1988). The

parameters of the transfer function are considered

constant under an operating range around the operat-

ing point. In this paper, only disturbances around the

operating point are considered. Thus, the variation of

the transfer delays for these discharges is sufﬁciently

small in comparison with the chosen control period,

and will not have a signiﬁcant inﬂuence on the strat-

egy effectiveness. If large operating conditions are

considered, and/or in the case of the ”small” control

period, it is necessary to consider several time delays

function of discharge value, as proposed in (Duviella

et al., 2006). For each OCRS (see Figure 2), the trans-

fer time delay τ

is obtained from the step response of

the corresponding transfer function. It is chosen as the

time value for which Π

percent of step is reached.

The percentage Π

can be tuned from simulation.

In the case of gridded systems, the value of the

transfer time delay between the measurement point

and the gate G

depends on the path to go from

the measurement point M

to the gate G

(see Figure

2). P

b,d

is the set of direct paths to go from the HYS

b to the HYS d, and P

b,d

is one of the direct paths to

go from the HYS b to the HYS d, such as P

b,d

∈ P

b,d

where 1 ≤ v ≤ ρ

b,d

, with ρ

b,d

the total number of paths

which compose P

b,d

. A direct path from M

to G

, is

a path where not other measurement point can be met

between M

and G

The transfer time delays between the measure-

ment point M

and the gate G

are computed by

considering each path and constitute the vector t

, j

(ρ

b,d

× 1):

, j

, t

, j

, ... , t

b,d

, j

. (1)

Thereafter, the transfer time delay between M

and G

, is computed according to the selected path

b,d







, j

= t

r< j

∑

r=n

r,r+1

≤ j ≤ n,

(2)

Figure 2: Transfer delays between the measurement point

and gates G j.

where n

is the ﬁrst gate downstream M

, v is the index

of the path P

b,d

, and τ

r,r+1

is the transfer time delay

between each gate along the path P

b,d

as illustrated in

Figure 2.

Then, the new setpoints must be assigned to the

gates at a time instant taking into account the trans-

fer time delays which are expressed according to the

sampling period T

, j



, j



+ 1, (3)

where

denotes the integer part of x.

The measured water quantity in M

, following the

path with index v, will arrive on gate G

at the time:

, j



k + kd

, j



. (4)

Finally, the transfer time delays between the mea-

surement point M

and the gate G

are expressed by

the vector T

, j

(ρ

b,d

× 1):

, j

, T

, j

, ... , T

b,d

, j

. (5)

The complex hydrographic network representation, as

well as the identiﬁcation of the transfer time delays,

constitute an essential step for the design of reactive

control strategies.

4 SUPERVISION AND

RESOURCE ALLOCATION

Supervision and hybrid control accommodation

framework is depicted in Figure 3. The hydrographic

network is represented by a set of m measurement

points M

and n gates G

locally controlled. For each

gate G

, a weekly objective discharge q

ob j

and sea-

sonal weights λ

and µ

are given by the Management

Objective Generation module according to the water

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

314

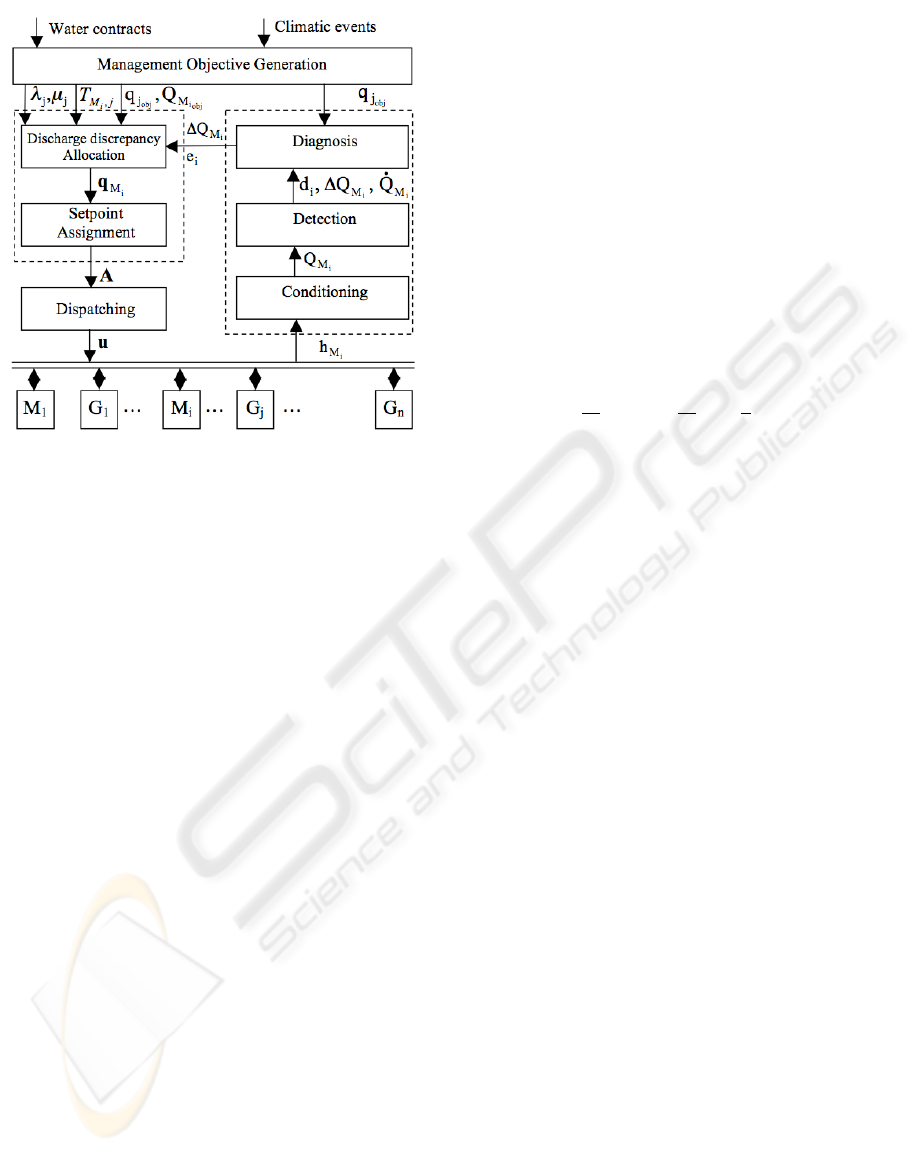
Figure 3: Supervision and hybrid control accommodation

framework.

contracts and climatic events. The weekly measure-

ment point objective discharge Q

ob j

is known.

For each measurement point M

; i = 1,...,m, dis-

charge supervision consists in monitoring discharge

disturbances and diagnosing the resource state, simul-

taneously. Limnimeter measurements are conditioned

by a low-pass ﬁlter on a sliding window which re-

moves wrong data due to transmission errors for in-

stance. Based on the discharge value Q

which is

determined at each sample time kT

, detection and

diagnosis automata are used respectively to detect a

discharge discrepancy superior or inferior than a de-

tection threshold d

around Q

ob j

, and to diagnose

the resource states (Duviella et al., 2007). According

to the resource state and the discharge discrepancy

∆Q

= Q

ob j

− Q

, the hybrid control accommo-

dation consists in determining the setpoints q

, and

in assigning them to the gates taking into account the

hydraulic system dynamics. The resource allocation

consists in recalculating setpoints with a goal to route

resource in excess to dams and to dispatch amongst

the users the resource in lack. At each sample time

, the resource allocation leads to the determina-

tion of allocation vector q

which is composed of

the new computed setpoints. The allocation vector is

computed according to the resource state e

tacking

into account the seasonal weights λ

and µ

If the resource state is no diagnose situation, the

setpoints are the objective discharges q

ob j

. The allo-

cation vector is such as:

R(i,1)

ob j

...δ

R(i, j)

ob j

...δ

R(i,n)

ob j

(6)

where

corresponds to the higher rounding of x,

n is the total number of gates, and δ

the Kronecker

index, is equal to 1 when a = b, and equal to 0 if not.

If the resource state is such as discharge is

in lack or in excess, the water resource is allocated

among the gate downstream the measurement point

, according to the weights λ

and µ

. The allo-

cation strategy consists in optimizing a cost function

by linear programming method for each measurement

point. The cost function f

is deﬁned as the weighted

sum of the differences between the setpoint q

and the

objective q

ob j

for each gate G

, at time kT

∑

j=1



R(i, j)

i, j

− q

ob j

)



, (7)

with χ

i, j

= γ

+(γ−1)

, γ =

(sign(∆Q

)+1).

The optimization is carried out under constraints:







∑

j=1



R(i, j)(q

− q

ob j

)



= ∆Q

min

≤ q

max

(8)

where q

min

and q

max

are respectively the minimum

and maximum discharges given by gate, river or canal

characteristics. In this case, the allocation vector q

is such as:

R(i,1)

... δ

R(i, j)

... δ

R(i,n)

(9)

Then, to synchronize the gate control with the wa-

ter lacks or excess due to the disturbances, the set-

points must be assigned at a time instant tacking into

account the transfer time delays T

, j

between the

measurement point M

and the gate G

5 SETPOINT ASSIGNMENT

RULES

The setpoint assignment consists in taking into ac-

count the transfer delays before the dispatching of

the new computed setpoints at the gates. In the case

of gridded systems, two different setpoint assignment

rules are proposed.

The ﬁrst rule consists in considering only one

transfer delay T

, j

from each measurement point M

to each gate G

, whatever existing several paths to go

from M

at the gate G

. The transfer delay between

and G

is selected as the direct path between M

and G

, which have the greatest supplying discharge

proportion. The following assumptions are consid-

ered:

SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME DELAYS FOR WATER-ASSET MANAGEMENT

OF NETWORKED OPEN-CHANNEL SYSTEMS

315

Table 2: Assignment function of α and β matrices.

Input: weighted digraph.

Output: α

matrix, β

matrices

Initialization of the diagonal of α

to 0

Initialization of β

to 0

g ← ﬁrst gate successor of M

Run (M

, g, 1, α

, β

)

Run (M

, c, p, α

, β

)

For any successor d of c

← p.w

If d is a gate

Run (M

, d, p

, α

, β

)

(d, d) ← α

(d, d) + p

l = 1

While (β

(l, d) 6= 0)

l + +

EndWhile

(l, d) ← p

EndIf

EndFor

- if the discharge proportion β

(v, j) resulting from

and supplying G

by a single path P

b,d

, is weak,

the discrepancy allocation will be weak also,

- if the discharge proportion β

(v, j) resulting from

and supplying G

by a single path P

b,d

, is impor-

tant, the discrepancy allocation will be important also.

The supplying discharge proportion β

(ρ

×n),

where ρ

is the maximum number of paths between

and the gates G

, is computed for each measure-

ment point M

according to the algorithm given in Ta-

ble 2 and the weighted digraph of the system.

Thus, the set of allocation dates starting from M

denoted T

(1 × n) updated at each sampling period

and expressed by:

= [T

... T

, j

... T

], (10)

where



, j

= 0, if β

(1, j) = 0

, j

= T

, j

, otherwise,

(11)

and v such as β

(v, j) = max

l∈

[

1,ρ

]

(l, j). When

(1, j) = 0 there is no direct path between M

and

At each sample time kT

, the setpoint assignment

matrix A

× n), where H

is the allocation

horizon from M

, is scheduled according to T

and

. The ﬁrst row of A

contains the setpoints to be

assigned to each gate from M

at the date (k +1)T

, the

row the ones to be assigned at the date (k + h)T

as deﬁned in equation 12, the last row the ones to be

assigned at the date (k + H

If T

( j) ≥ (k + h)T

(h, j) = q

( j),

Else

If 1 ≤ h < H

(h, j) = A

k−1

(h + 1, j)

Else

(h, j) = q

ob j

Endif

(12)

and A

(h, j) = q

ob j

The setpoints are dispatched with the control pe-

riod T

= κT

, where κ is an integer. The control set-

point vector denoted u (1 × n) is updated at each date

, where k

, thanks to the assignment matrix

and the α

(n×n) diagonal control accommoda-

tion matrix, with H =

max

1≤i≤m

) the control hori-

zon. For each measurement point M

, the α

matrix,

the role of which is to capture the measurement point

inﬂuence on the gates, must be determined. In order

to generate the α

matrix, the weighted digraph (see

Figure 1.c and 1.d) is browsed using the algorithm

given in Table 2, for each measurement point M

. The

control setpoint vector u

(1 × n) is calculated by:

( j) =

∑

i=1

( j, j)A

(1, j). (13)

The second rule consists in considering the sev-

eral direct transfer delays T

, j

from each measure-

ment point M

to each gate G

. The set of alloca-

tion dates starting from M

is denoted T

(ρ

× n),

where ρ

is the maximum number of paths between

the measurement points M

and the gates G

. The ma-

trix T

is updated at each sampling period T

and ex-

pressed by:

= [T

... T

, j

... T

], (14)

where T

, j

is the set of the transfer time delays be-

tween the measurement point M

and the gate G

. The

value of T

, j

(l) is ﬁxed to 0 for ρ

< l ≤ ρ

, i.e.

when the length ρ

of the T

, j

is smaller than ρ

In this case, the setpoint assignment matrix A

× n) is scheduled, at each sample time kT

, ac-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

316

cording to T

and q

If ∃v such as T

(v, j) ≥ (k + h)T

(h, j) =

∑

v=1

.β

(v, j).q

( j)

Else

If 1 ≤ h < H

(h, j) = A

k−1

(h + 1, j)

Else

(h, j) = α

( j, j).q

ob j

Endif

(15)

where ϕ

= 1 if T

(v, j) ≥ (k + h)T

, ϕ

= 0 other-

wise, and A

(h, j) = α

( j, j).q

ob j

The control setpoint vector denoted u (1×n) is up-

dated at each date k

, thanks to the assignment ma-

trix A

, with H =

max

1≤i≤m

) the control horizon.

The control setpoint vector u

(1 × n) is calculated

by:

( j) =

∑

i=1

(1, j). (16)

The setpoint dispatching leads to the application of

the most recently calculated setpoints. This method

increases the control strategy reactivity, because dis-

charge variations between two control dates are taken

into account.

6 SIMULATION RESULTS

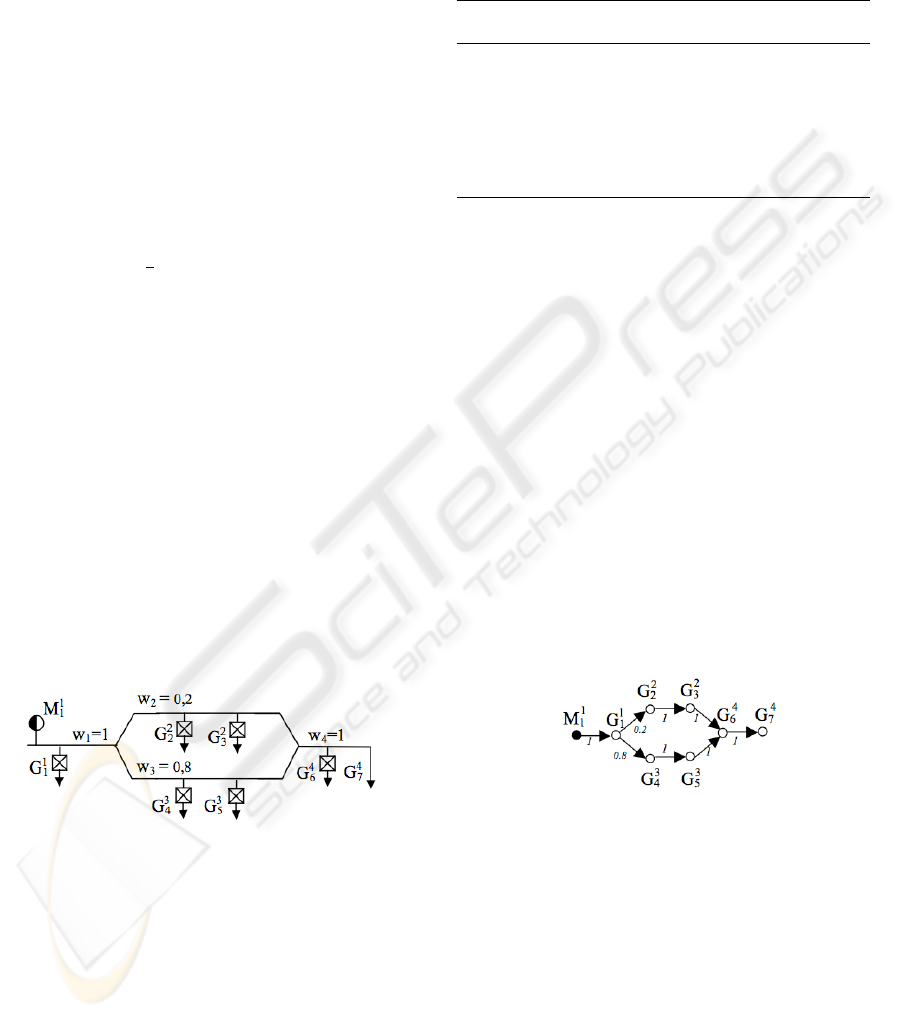
The proposed setpoints assignment rules have been

evaluated for a hydrographic system composed of one

diﬂuence and one conﬂuence (see Figure 4).

Figure 4: Hydrographic system composed of one diﬂuence

and one conﬂuence.

The hydrographic system is composed of 4 HYS,

equipped with 6 gates, G

to G

, and 1 measurement

point M

. The discharge downstream the gate G

fed

the HYS which is equipped with the gates G

to G

with the discharge proportion w

and the HYS which

is equipped with the gates G

to G

with the discharge

proportion w

. The discharge proportion w

is equal

to 0.2 and w

to 0.8. The gates G

which corresponds

to the canal outputs, is not controlled. The gate char-

acteristics, i.e. objective discharge q

ob j

, maximum

and minimum discharges q

j max

, q

j min

, and their asso-

ciated weights, are given in Table 3.

Table 3: Gate parameters.

Gate q

ob j

/s]

j min

/s]

j max

/s]

1.1 0.05 0.85 10 10

0.3 0.1 0.9 1 4

0.4 0.15 1.2 1 4

1.9 0.1 1.4 4 1

1.6 0.1 0.9 1 4

0.9 0.05 1.8 10 10

1.8 0.05 0.75 − −

The use of the proposed rules requires the identi-

ﬁcation of the transfer time delays. The set of HYS

which are characterized by trapezoidal proﬁle have

been modelled according to the transfer time delay

identiﬁcation steps. The matrix, T

, of transfer time

delays between M

and each gate, expressed in sec-

onds, are given by:



850 1750 2700 1450 2050 3750

0 0 0 0 0 2700



(17)

There are two identiﬁed transfer time delays be-

tween M

and G

; T

= 3750 s corresponds to the

path P

1,4

; T

= 2700 s corresponds to the path P

1,4

Then, the hydrographic system (see Figure 4) is

represented by the weighted digraph depicted in Fig-

ure 5 to determine the matrix R, and then, to deter-

mine the matrices α

and β

Figure 5: Graph for the determination of R and α

The matrix R is given by:

R =



1 0.2 0.2 0.8 0.8 1



. (18)

The diagonal matrix α

is given by:

= diag

{

1,0.2,0.2,0.8,0.8,1

}

(19)

The matrix β

is given by:



1 0.2 0.2 0.8 0.8 0.2

0 0 0 0 0 0.8



. (20)

The objective discharges of M

correspond to 8

/s. The hydrographic system is subjected to dis-

turbances upstream the measurement points M

(see

SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME DELAYS FOR WATER-ASSET MANAGEMENT

OF NETWORKED OPEN-CHANNEL SYSTEMS

317

Figure 6.a). The detection threshold is selected as

= 0.15 m

/s. Figure 6 shows discharges measured

on M

, and the new setpoints which have been dis-

patched at the gates which were controlled, i.e. G

(b) and G

in (c), and the discharges resulting at the

canal ends q

in (d) in case 1: the case where only

one transfer time delay is considered (the ﬁrst rule is

used without any assumption about the discharge pro-

portion values), the transfer time delay considered is

(dashed line), in case 2: the case where the ﬁrst

rule is applied, thus the time delay considered is T

(dotted line), and in case 3: the case where the second

rule is applied (continuous line).

Figure 6: Discharges in [m

/s] (a) Q

, (b) q

, (c) q

, and

(d) the resulting discharges q

Whatever the setpoint assignment rules used are,

there is a peak of approximately 0.15 m

/s on G

the 2

, 11

, 20

and 27

hours (see Figure 6.d),

due to the detection threshold d

and the occurrence

of the discharge discrepancies on Q

. When the

transfer time delay is T

, the setpoints are assigned

too late, and the discharges at the end of the hydro-

graphic system are not close to the objective value

7ob j

. These results show the importance of the trans-

fer time delay. The results are improved when the ﬁrst

rule is used with T

, because of better evaluation of

transfer time delay. Finally, the performances are also

improved when the second rule is applied, the effec-

tive transfer time delays are taken into account be-

cause all direct paths are considered. The maximum

and minimum discharges reached at G

and the wa-

Table 4: Criteria computed when the different rules are

used.

Case max(q

)

/s]

min(q

)

/s]

]

case 1 2.09 1.59 1815

case 2 1.99 1.63 1099

case 3 1.97 1.63 1057

ter volume V which was not allocated are displayed

in Table 4. The maximum discharge discrepancy at

corresponds to 9.5 % of the objective discharge

7ob j

when the second rule is used and to 10.5 % in

the other case. The second rule leads to spare an ad-

ditional water quantity of 42 m

during 32 hours, in

comparison to the use of the ﬁrst rule. The differ-

ences between the two strategies are weak. In addi-

tion, these differences decrease for hydrographic sys-

tems which are equipped by a great number of mea-

surement points, because, in this case, the number of

direct paths is weak.

7 CONCLUSION

The resource allocation and setpoint assignment rules

constitute a generic approach allowing the water re-

source valorization whatever the conﬁguration of the

hydrographic networks is. Multiple graph represen-

tations make it possible to identify the information

for implementing the proposed supervision and hy-

brid control accommodation strategy. Two rules of

setpoint assignment have been proposed, tested and

compared within the framework of a networked open-

channel system composed of one diﬂuent and one

conﬂuent. Although the second rule leads to the best

performances, its implementation is more complex

than the one for the ﬁrst rule. The choice between the

two strategies could be carried out only by consider-

ing the hydrographic system with this equipment.

REFERENCES

Cembrano, G., Wells, G., Quevedo, J., Perez, R., and Arge-

laguet, R. (2000). Optimal control of a water distribu-

tion network in a supervisory control system. Control

Engineering Practice, 8:1177–1188.

Chan, C., Kritpiphat, W., and Tontiwachwuthikul, P. (1999).

Development of an intelligent control system for a

municipal water distribution network. IEEE Canadian

conference on Electrical and Computer Engineering,

2:1108–1113.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

318

Chow, V. T., Maidment, D. R., and Mays, L. W. (1988).

Applied Hydrology. McGraw-Hill, New York, Paris.

Duviella, E., Chiron, P., and Charbonnaud, P. (2006). Hy-

brid control accommodation for water-asset manage-

ment of hydraulic systems subjected to large operating

conditions. ALSIS06, 1st IFAC Workshop on Applica-

tions of Large Scale Industrial Systems, Helsinki, Fin-

land, August 30-31 2006.

Duviella, E., Chiron, P., Charbonnaud, P., and Hurand, P.

(2007). Supervision and hybrid control accommoda-

tion for water asset management. Control Engineering

Practice (CEP), 15:17–27.

Faye, R. M., Sawadogo, S., Niang, A., and Mora-Camino,

F. (1998). An intelligent decision support system

for irrigation system management. IEEE Interna-

tional Conference on Systems, Man and Cybernetics,

SMC’98, October 11-14, San Diego, USA, 4:3908–

3913.

Islam, A., Raghuwanshi, N. S., Singh, R., and Sen, D. J.

(2005). Comparison of gradually varied ﬂow compu-

tation algorithms for open-channel network. Journal

of irrigation and drainage engineering, 131(5):457–

465.

Lisounkin, A., Sabov, A., and Schreck, G. (2004). Inter-

preter based model check for distribution networks.

IEEE international conference on industrial informat-

ics, INDIN’O4, 24-26 juin, pages 431–435.

Litrico, X. and Georges, D. (1999). Robust continuous-time

and discrete-time ﬂow control of a dam-river system.

(i) modelling. Applied Mathematical Modelling 23,

pages 809–827.

Malaterre, P.-O. and Baume, J.-P. (1998). Modeling and

regulation of irrigation canals: Existing applications

and ongoing researches. IEEE International Con-

ference on Systems, Man, and Cybernetics, 4:3850–

3855.

Mansour, H. E. F., Georges, D., and Bornard, G. (1998).

Optimal control of complex irrigation systems via

decomposition-coordination and the use of augmented

lagrangian. IEEE, International Conference on Con-

trol Applications, Trieste, Italy, pages 3874–3879.

Naidu, B. J., Bhallamudi, S. M., and Narasimhan, S.

(1997). GVF computation in tree-type channel net-

works. Journal of hydraulic engineering, 123(8):700–

708.

SETPOINT ASSIGNMENT RULES BASED ON TRANSFER TIME DELAYS FOR WATER-ASSET MANAGEMENT

OF NETWORKED OPEN-CHANNEL SYSTEMS

319