CRONE OBSERVER
Definition and Design Methodology
Jocelyn Sabatier, Patrick Lanusse and Mathieu Merveillaut
LAPS - ENSEIRB - Université Bordeaux 1 - Equipe CRONE – UMR 5218 CNRS
351, Cours de la Libération, 33405 Talence cedex, France
Keywords: Robust observer, CRONE observer, Fractional Order Controller, CRONE control.
Abstract: CRONE control, robust control methodology based on fractional differentiation, is applied to state observer
design. State observation can indeed be viewed as a regulation problem given that the goal of a state
observer is to cancel the observation errors in spite of measurement noises, disturbances and plant
perturbations. This conclusion has been used recently to define a new class of state observers known in the
literature as “dynamic observers” or “input-output observer”. It is based on the observation error dynamic
feedback. In this paper, this idea is used to define the CRONE observer design methodology. Performance
robustness of the obtained observers versus plant perturbations is analysed. As for CRONE control,
fractional differentiation in the definition of an equivalent open loop transfer function permits to reduce the
number of parameters to be optimised.
1 INTRODUCTION
In many industrial applications of control, controlled
variables cannot be directly measured by sensors. In
such a situation, these variables can be reconstructed
with a Luenberger type observer (Luenberger,
1971). However, it is really difficult to take into
account modelling errors and disturbances in the
synthesis the observer gains. We recently faced with
this problem, for the speed control of a steel rolling
mill, speed of the load being not measured due the
high temperatures and maintenance costs (Sabatier
et al., 2003). Moreover, some parameters of the
system were not known with accuracy (such as
sliding viscous coefficients). To solve this problem,
a Luenberger observer was associated with a
CRONE controller (Oustaloup, 1991). In this
application of CRONE control, an overestimation of
the plant uncertainties was required to take into
account bias introduced by the observer due to
differences between plant and observer model
behaviours as the time of plant parameters
variations. To reduce the resulting conservatism, a
robust observer has to be designed, robustness of the
observation error convergence to zero in spite of
disturbances and plant perturbation being addressed.
A solution to obtain such an observer, consists in
considering observation problem as a classic
regulation problem and thus to construct a feedback
loop with the available information (plant input and
output), whose goal is to cancel the observation
errors in spite of measurement noise, disturbances
and plant perturbations. This new concept was
recently published and applied on a real system
(Marquez, 2003) (Marquez and Riaz, 2005). In this
paper, a CRONE controller is introduced in the
feedback loop in order to take into account the
disturbances and the model perturbation. In
comparison with the H
∞
approach used by Marquez,
plant model perturbations are taken into account in a
structured form with no overestimation, thus,
without conservatism. Due to the introduction of
fractional differentiation in the CRONE approach,
an open loop transfer function with only three
parameters (just like a PID controller) has to be
optimised to simultaneously reduce the effects of
disturbances and model perturbation on the
observation error. Another contribution of the paper
is the extension of the idea by Marquez to the
problem of state observation with unknown input.
The paper is organised as follows. Section 2 presents
the dynamic output feedback based observer concept
developed in (Marquez, 2003) (Marquez and Riaz,
2005) and extends it to observation with unknown
input. Section 3 gives some generalities on CRONE
control. In section 4, application of CRONE control
421
Sabatier J., Lanusse P. and Merveillaut M. (2007).
CRONE OBSERVER - Definition and Design Methodology.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 421-429
DOI: 10.5220/0001637404210429
Copyright
c
 SciTePress

to state observation problem is developed thus
defining an observer that will be referred to as a
CRONE observer in future developments.
2 DYNAMIC OUTPUT
FEEDBACK BASED
OBSERVER
2.1 Presentation
Dynamic output feedback based observer concept
was introduced in (Marquez, 2003) and (Marquez
and Riaz, 2005) in which the observation problem is
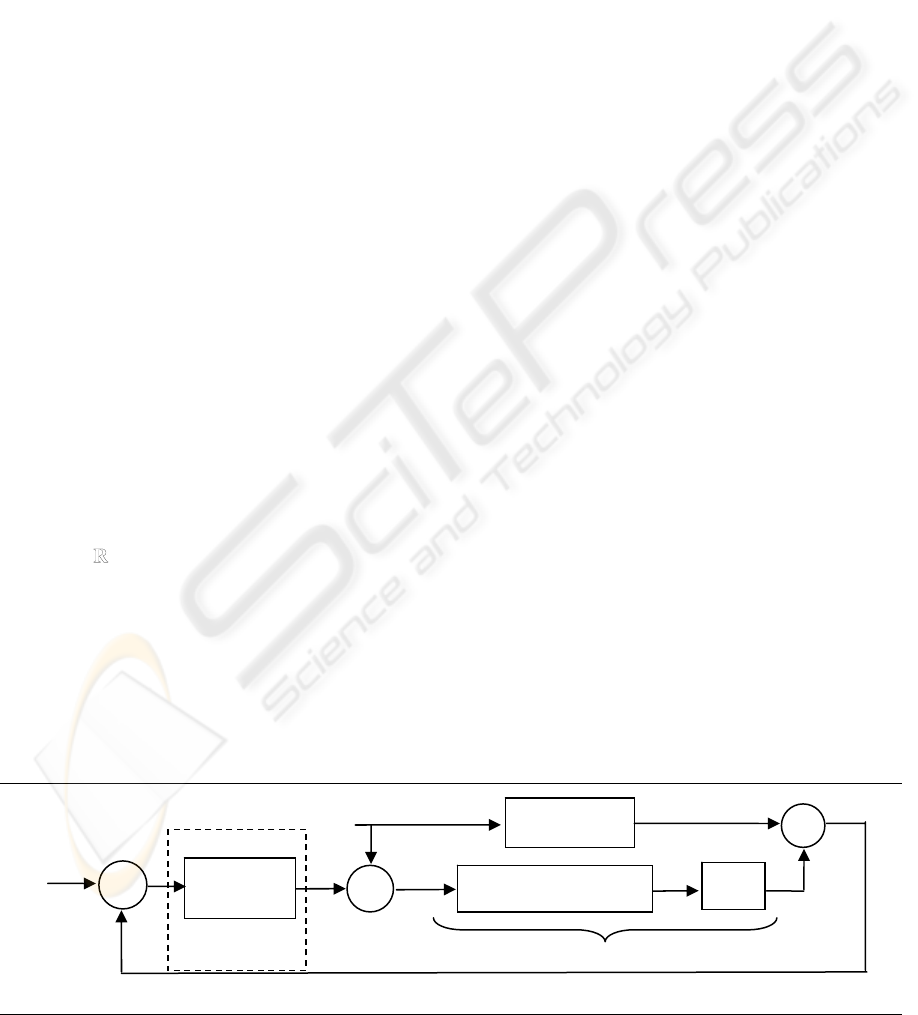
solved using the feedback diagram of Fig. 1. The
plant P, the model M and the dynamic controller K
are supposed single input / single output systems
represented by the state space descriptions:
() () ()
() ()
⎩
⎨
⎧
=
+=
tCxty
tButAxtx
P
&
: (1)
() () () () () ()()
() ()
⎪
⎩
⎪
⎨
⎧
=
++=+=
txCty
twtuBtxAtBvtxAtx
M
ˆˆ
ˆˆ
ˆ
:
&
(2)
() () ()
() () ()
()
() ()
⎪
⎩
⎪
⎨
⎧
=
−+=
−=
txCtw
txtxCBtxA
tBtxAtx
K
KK
KK
KKkK
ˆ
:
ε
&
(3)
State x(t) is supposed not measurable and
(
)
tx
ˆ
denotes the estimated state. All the elements of
matrices and vectors in (1) to (3) are supposed
element of
.
Figure 1 clearly shows that the goal of the used
feedback structure is to cancel the observation error
() () ()
txtxt
ˆ
−=
χ
by cancelling the error signal
() ()
tyty −=
ˆ
ε
. Time derivative of the observation
error
() () ()
txtxt
ˆ
&&
&
−= χ , is thus given by :
() () () () ()
(
)()
() ()
txBCtA
twtuBtAxtButAxt
KK
−=
+−−+=
χ
χ
&
. (4)
Using controller state space description (3), a state
space description for the system in Fig. 1 involving
the observation error is thus:
(5)
Matrix A
O
in relation (5) is also the state matrix of
the feedback system in Fig. 2. Such a remark permits
to demonstrate the following theorem.
Theorem (Marquez, 2003)
State
(
)
tx
ˆ
exponentially converge to the state x(t)
with the feedback structure of Fig. 1, if all matrix A
O
eigenvalues of has a strictly negative part or if the
system in Fig. 2 is internally stable.
2.2 Extension to State Observation
with Unknown Input
The problem of state observation with unknown
input is now addressed using the dynamic output
feedback structure of Fig. 3.
It is supposed that the plant P and the model M are
described by the following state space descriptions:
(
)()()
() ()
⎩
⎨
⎧
=
+=
tCxty
tButAxtx
P
&
:
(6)
(
)
(
)
(
)
() () ()
() ()
⎪
⎩
⎪
⎨
⎧
=
−=
+=
txCty
tEytztx
tBvtNztz
M
ˆˆ
ˆ
:
&
(7)
Observation error dynamics is thus defined by:
(
)
(
)
(
)
(
)()()
(
)()
tyEtztButAxtxtxt
&
&
&
&
&
−−+=−=
ˆ
χ (8)
or using relations (6) and (7):
(
)
(
)
(
)()
() () () ()
tBvtECButButxN
tECAxtNECxtAxt
−++−
+−=
ˆ
χ
&
. (9)
Figure 1: Dynamic output feedback based observer.
P
(
)
(
)
(
)
tBvtxAtx +=
ˆ
ˆ
&
u(t)
v(t)
K
(s)
0
Dynamic
controller
+
-
+
C
()
ty
ˆ
(
)
tx
ˆ
+
-
ε (t)
Model M
w(t)
y
(t)
(
)
()
()
()
()
()
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
tx
t
A
tx
t
ACB
BCA
tx
t
K
O
KKK
K
K
χχχ
&
&
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
422

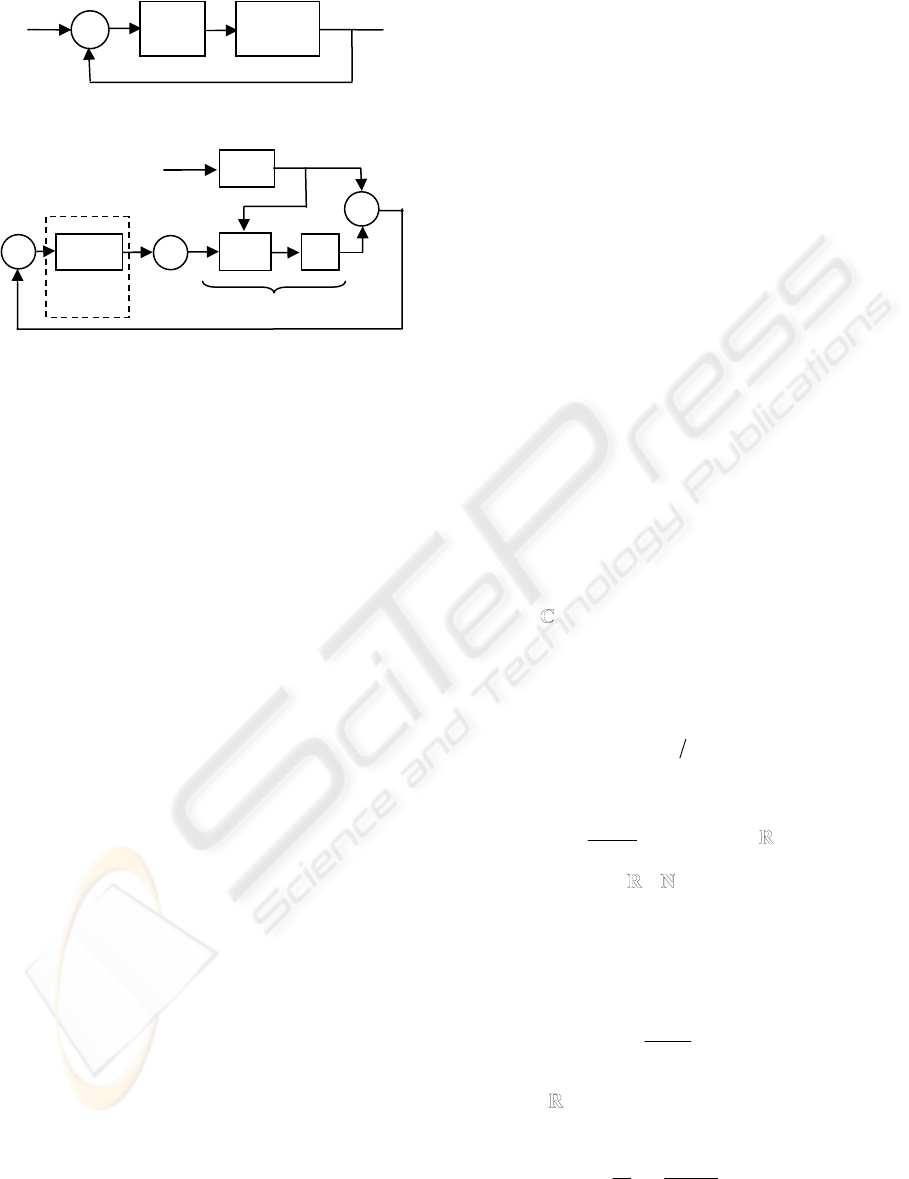
Figure 2: Feedback system with state matrix A
O.
Figure 3: Dynamic output feedback based observer with
unknown input.
Suppose now that matrix E is such that
0=+ ECBB or
()
*
CBBE −= (10)
in which
()
*
CB denotes the generalised inverse of
CB if it exits. Equation (9) thus becomes:
() () () () ()
(
)
tBvtxNtECAxtNECxtAxt −−+−=
ˆ
χ
&
,(11)
or using the state space description of the controller
K of relation (3):
() () () ()
() ()
() ()
⎪
⎩
⎪
⎨
⎧
+=
−−
+−=
χ
χ
CBtxAtx
txBCtxN
tECAxtNECxtAxt
KKKK
KK
&
&
ˆ
. (12)
Let now
ECIP += and thus IPEC −= (13)
then
()()
PANNP
AIPIPNAECANECA
++−=
−+−
−
=+−
. (14)
If it is now imposed now that
0=+− PANP and thus
1−
= PAPN , (15)
equation (12) becomes:
()
()
()
()
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
tx
t
ACB
BCN
tx
t
KKK
K
K
χχ
&
&
. (16)
Relation (16) is similar to relation (5) and thus
highlights, given the analysis following relation (5),
that the observation error converges exponentially to
zero if controller K internally stabilise the feedback
system in Fig. 2, model M being defined by:
(
)()()
() ()
⎩
⎨
⎧
=
+=
tCty
tBvtNt
M
χ
χχ
&
:. (17)
3 CRONE CSD PRINCIPLES
3.1 Introduction to Fractional
Integro-Differentiation
The first definitions of fractional order
differentiation (or integration) were given by
Leibniz and Euler at the end of the 17th and during
the 18th century. In the 19th century many
mathematicians generalized these definitions:
Laplace, Lacroix, Fourier, Liouville, Abel,
Hargreave, Riemann etc. In 1869 Sonin extended the
Cauchy integral to fractional integration orders and
the Riemann-Liouville definition was finally
proposed.
Operational calculus can also be used. Let y(t) be the
order n derivative of the causal signal x(t):
(
)
{
}
(
)() txDtxty
nn
==
(18)
with n
∈ and where D is the differentiation
operator. If the real part of n is negative, then y(t) is
in fact the order -n integral of x(t).
The transfer function of the linear operator D
n
is
defined by the Laplace transform:
(
)
(
)
{
}(){} .
n
stxLtyLsD ==
(19)
Its impulse response is given by:
() {}
()
()
t
n
t
sLtd
n
n
H
1
1
−Γ
==
−−
−
if Re[n]∈
-
and Re[n]≠0,
or
0
≠
∀
t
if Re[n]∈
+
- and Re[n]=0 (20)
where
Γ (.) and H(.) denote the gamma and
Heaviside functions.
Convoluting d(t) and x(t), y(t) can be computed
using the following integrals:
()
()
()
∫
−
−Γ
=
−−
t
n
dtx
n
ty
0
1
θθ
θ
(21)
if
Re[n]∈
-
and
Re[n]≠0 which is the Riemann-
Liouville definition, and
()
()
()
∫
−
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
=
−−
t
nm
m
dtx
ndt
d
ty
0
1
θθ
θ
(22)
K
(s)
0
+
-
M
odel M
y
(
t
)
P
u(t)
+
v(t)
K
(s)
Dynamic
controller
-
C
(
) ty
ˆ
()
tx
ˆ
+
-
ε
(t)
Model M
w(t)
y
(t)
CRONE OBSERVER - Definition and Design Methodology
423

if Re[n]∈
+
-
and Re[n]=0, where m is defined
by the integer part of the real part of n. It is obvious
that a specificity of this fractional differentiation, is
that it takes into account all the past of signal x(t). A
fractional-order system can be considered as an
infinite order rational system. Thus, fractional
systems are often used to model distributed
parameter systems. As fractional operators can
replace high order transfer functions in system-
identification or control-system design, they are also
used to determine models or controllers with few
tuning parameters.
Since the sixties, some electrical circuits have been
proposed for synthesizing half order differentiators
(Suezaki and Takahashi,1966), (Dutta Roy, 1970),
(Biorci and Ridella, 1970), (Ichise et al., 1971),
(Oldham, 1973). From 1975 on, Oustaloup et al.
proposed methodologies for synthesizing band-
limited differentiators whose orders are fractional
(Oustaloup, 1975). Since 1990, they have extended
this to complex fractional order differentiators
(Oustaloup et al., 1990), (Oustaloup et al., 2000) and
have applied it to robust control design. Fractional or
non-integer order systems are also termed Warburg
impedance or Constant Phase Element (CPE), and
are associated to long-time memory behaviours.
3.2 Introduction to the CRONE
Methodology
The CRONE control-system design is based on the
common unity-feedback configuration (Fig. 4). The
robust controller or the open-loop transfer function
is defined using fractional order integro-
differentiation. The required robustness is that of
both stability margins and performance, and
particularly peak value M
r
(called resonant peak) of
the common complementary sensitivity function
T(s).
Figure 4: Common CRONE control-system diagram.
Three CRONE control design methods have been
developed, successively extending the application
field.
The third CRONE control generation must be used
when the plant frequency uncertainty domains are of
various types (not only gain-like). It is based on the
definition of a generalized template described as a
straight line in the Nichols chart of any direction
(complex fractional order integration), or by a multi-
template (or curvilinear template) defined by a set of
generalized templates.
An optimization allows the determination of the
independent parameters of the open loop transfer
function. This optimization is based on the
minimization of the stability degree variations, while
respecting other specifications taken into account by
constraints on sensitivity function magnitude. The
complex fractional order permits parameterization of
the open-loop transfer function with a small number
of high-level parameters. The optimization of the
control is thus reduced to only the search for the
optimal values of these parameters. As the form of
uncertainties taken into account is structured, this
optimization is necessarily nonlinear. It is thus very
important to limit the number of parameters to be
optimized. After this optimization, the
corresponding CRONE controller is synthesized as a
rational fraction only for the optimal open-loop
transfer function.
The third generation CRONE CSD methodology, the
most powerful one, is able to design controllers for
plants with positive real part zeros or poles, time
delay, and/or with lightly damped modes (Oustaloup
et al.,1995). Associated with the w-bilinear variable
change, it also permits the design of digital
controllers. The CRONE control has also been
extended to linear time variant systems and
nonlinear systems whose nonlinear behaviors are
taken into account by sets of linear equivalent
behaviors (Pommier et al., 2002). For MIMO
(multivariable) plants, two methods have been
developed (Lanusse et al., 2000). The choice of the
method is made through an analysis of the coupling
rate of the plant. When this rate is reasonable, one
can opt for the simplicity of the multi SISO
approach.
3.3 Third Generation CRONE
Methodology
Within a frequency range [ ω
A
, ω
B
] around open-loop
gain-crossover frequency
ω
cg
, the Nichols locus of a
third generation CRONE open-loop is defined by an
any-angle straight line segment, called a generalized
template (Fig. 5).
The generalized template can be defined by an
integrator of complex fractional order n whose real
part determines its phase location at frequency
ω
cg
,
that is –
Re
/i
(n)π/2, and whose imaginary part then
determines its angle to the vertical (Fig. 5).
-
+
e(t)
y
(t)
u(t)
d
u
(t)
n
m
(t)
d
y
(t)
C(s)
P
(s)
β
(s)
+
+
+
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
424

()
()
(
)
b-q
b
l
h
a
l
h
b
s
s
e
s
s
Cs
sign
i
/i
sign
1
1
1
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
ℜ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
=
ω
ω
α
ω
ω
αβ
Figure 5: Generalized template in the Nichols plane.
The transfer function including complex fractional
order integration is:
()
(
)
b
ba
b
ss
bs
-sign
i
cg
i/
cg
sign
Re
2
cosh)(
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
ωω
π
β
(23)
with n = a + ib
∈
i
and ω ∈
j
, and where
i
and
j
are respectively time-domain and frequency-domain
complex planes. In (Hartley and Lorenzo, 2005) a
physical interpretation of such a complex order
operator is proposed.
The definition of the open-loop transfer function
including the nominal plant must take into account:
- accuracy specifications at low frequencies;
- the generalized template around frequency
ω
cg
;
- plant behaviour at high frequencies while
respecting the control effort specifications at these
frequencies.
Thus, the open-loop transfer function is defined by a
transfer function using band-limited complex
fractional order integration:
() () () ()
ssss
hl
ββββ = , (24)
with:
(25)
21
2
1
r
2
0
r
0
11
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
ω
ω
ω
ω
α
(26)
where
β
l
(s) is an integer order n
l
proportional
integrator:
()
l
1
ll
n
l
s
Cs
⎟
⎠
⎞
⎜
⎝
⎛
+=
ω
β
(27)
- where
β
h
(s) is a low-pass filter of integer order n
h
:
()
h
1
h
h
n
h
s
C
s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
ω
β
(28)
with
2/
22
2
l
n
cgl
cg
l
C
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
ωω
ω
and
2/
2
2
1
h
n
h
cg
h
C
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
ω
ω
(29)
The optimal open loop transfer function is obtained
by the minimization of the robustness cost function
(
) - MTJ
P
r0
,
j sup ω
ω
= , (30)
where M
r0
is the resonant peak set for the nominal
parametric state of the plant, while respecting the
following set of inequality constraints for all plants
(or parametric states of the plant) and for
ω ∈
+
:
(
)
(
) ωω
l
j inf TT
P
≥
and
() () TT
P
ωω
u
j sup ≤
, (31)
(
)
(
)
SS
P
ωω
u
j sup ≤ ,
()
(
)
CSCS
P
ωω
u
j sup ≤
and
(
) ()
PSPS
P
ωω
u
j sup ≤ , (32)
with
()
(
)
(
)
() ()
()
() ()
()
()
() ()
()
()
() ()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
=
+
=
+
=
+
=
sPsC
sG
sPS
sPsC
sC
sCS
sPsC
sS
sPsC
sPsC
sT
11
1
1
1
(33)
As the uncertainties are taken into account by the
least conservative method, a non-linear optimization
method must be used to find the optimal values of
three independent parameters. The parameterization
of the open-loop transfer function by complex
fractional orders, then simplifies the optimization
considerably. During optimization a complex order
has the same function as a whole set of parameters
found in common rational controllers.
When the optimal nominal open-loop transfer is
determined, the fractional controller K
F
(s) is defined
by its frequency response:
()
()
()
ω
ω
β
ω
j
j
j
0
F
P
K =
, (34)
where P
0
(j ω ) is the nominal frequency response of
the plant.
The parameters of a rational transfer function K
R
(s)
with a predefined low-order structure are tuned to fit
the ideal frequency response K
F
(j ω ). The rational
integer model on which the parametric estimation is
based, is given by:
|
β
(j
ω
)
|
dB
arg
β
(j
ω
)
0
-π
0
-π/2
ω
cg
ω
A
ω
B
-aπ/2
f(b,a)
CRONE OBSERVER - Definition and Design Methodology
425

()
()
()
sA
sB
sK =
R
, (35)
where B(s) and A(s) are polynomials of specified
integer degrees n
B
and n
A
. Any frequency-domain
system-identification technique can be used. An
advantage of this design method is that whatever the
complexity of the control problem, satisfactorily low
values of n
B
and n
A
, usually around 6, can be used
without performance reduction.
4 CRONE OBSERVER
Robustness considerations versus plant perturbation
are also addressed in (Marquez, 2003) in an H
∞
framework for the synthesis of an dynamic output
feedback based observer. In this paper, robustness to
plant perturbation is taken into account with
CRONE Control, thus leading to a new formulation
of in the CRONE control-system design
methodology.
4.1 Plant Perturbations and
Disturbance Rejection Effects
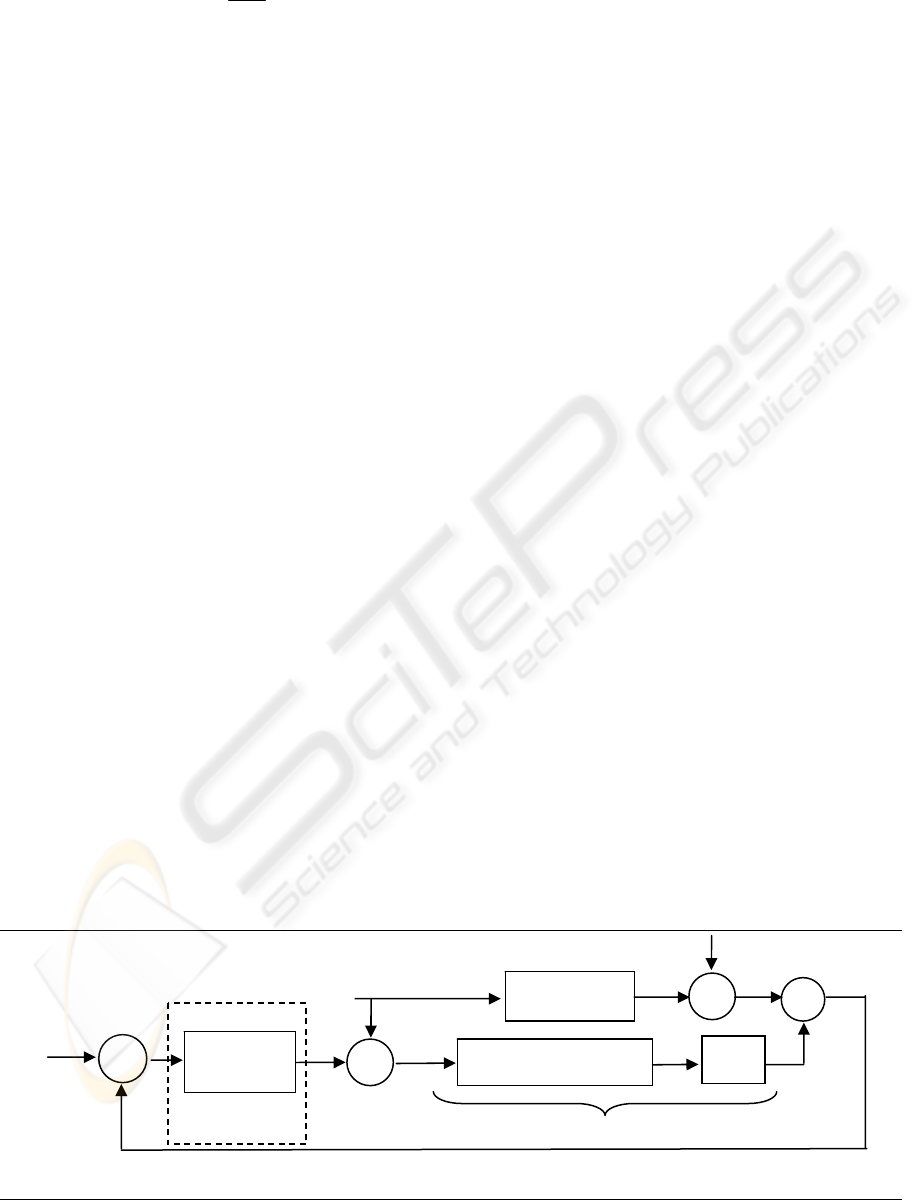
It is now supposed that the plant whose state is
estimated is submitted to perturbations. Effects of
these perturbations but also effects of output
disturbances d
y
(t) and measurement noises n(t) on
the estimation error are now studied. Control
diagram of Fig. 6 is considered.
Using the notations previously introduced for the
plant P, the model M and the controller K, the
following state space description are now
manipulated:
() ( )()
(
)()
(
)()
() () () ()
⎩
⎨
⎧
++=
+Δ++Δ+=
tntdtCxty
tdtuBtxAtx
P
y
uBA
&
: (36)
() () () () () ()()
() ()
⎪
⎩
⎪
⎨
⎧
=
++=+=
txCty
twtuBtxAtBvtxAtx
M
ˆˆ
ˆˆ
ˆ
:
&
(37)
(
)
(
)
(
)
() () () ()
()
()
() ()
⎪
⎩
⎪
⎨
⎧
=
−+++=
−=
txCtw
txCBtntdtCxBtxA
tBtxAtx
K
KK
KyKK
KKkK
ˆ
:
ε
&
(38)
Δ
A
and Δ
B
are real matrices of appropriate
dimensions that models plant perturbations.
At time t = 0, it is supposed that
()
00
=
K
x ,
(
)
0
0 xx
=
,
(
)
00
ˆ
=
x and thus
()
00
0
χ
χ
=
= x .
Laplace transform applied to relations (36) to (38)
thus lead to:
(
)
[
]
(
)()()
() () () ()
⎩
⎨
⎧
++=
Δ++=Δ+−
snsdsCxsy
suBsxAsI
P
y
BA
0
:
χ
(39)
[
]
(
)()()()
() ()
⎩
⎨
⎧
=
+=−
sxCsy
swsuBsxAsI
M
ˆˆ
ˆ
:
(40)
and
() []
() () ()
()
()
() ()
⎪
⎩
⎪
⎨
⎧
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
++
−=
−
sxCsw
sxCB
snsdsCxB
AsIsx
K
KK
K
yK
KK
ˆ
:
1
. (41)
At time t = 0, it is supposed that
()
00
=
K
x ,
(
)
0
0 xx
=
,
(
)
00
ˆ
=
x and thus
()
00
0
χ
χ
=
= x .
Laplace transform applied to relations (36) to (38)
thus lead to:
(
)
[
]
(
)()()
() () () ()
⎩
⎨
⎧
++=
Δ++=Δ+−
snsdsCxsy
suBsxAsI
P
y
BA
0
:
χ
(39)
[
]
(
)()()()
() ()
⎩
⎨
⎧
=
+=−
sxCsy
swsuBsxAsI
M
ˆˆ
ˆ
:
(40)
Figure 6: Dynamic output feedback based observer.
P
(
)
(
)
(
)
tBvtxAtx +=
ˆ
ˆ
&
u(t)
v(t)
K
(s)
0
Dynamic
controller
+
-
+
C
()
ty
ˆ
(
)
tx
ˆ
+
-
ε
(t)
Model M
w(t)
d
y
(t)+n(t)
y
(t)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
426

() []
() ()
(
)
()
()
() ()
⎪
⎩
⎪
⎨
⎧
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
++
−=
−
sxCsw
sxCB
snsdsCxB
AsIsx
K
KK
K
yK
KK
ˆ
:
1
. (41)
Difference of state equations of representations (39)
and (40) gives:
() [] ()
[
] ()
( )() () ()()
swsuBsuB
sxAsIsxAsI
B
A
+−Δ++=
−−Δ+−
0
ˆ
χ
(42)
and thus using output equation of representation
(41):
() [] () [] ()
( )() () ()()
sxCsuBsuB
sxAsIsxAsI
KKB
A
+−Δ++=
−−Δ+−
0
ˆ
χ
(43)
Let K(s) denotes the transfer function of the
controller K, with:
() []
KKK
BAsICsK
1−
−= , (44)
Then relation (43) becomes:
() [] ()
[
] ()
( )() ()
[] () () ()
[] () ()
()
snsdBAsIBC
sxsxCBAsIBC
sBusuB
sxAsIsxAsI
yKKK
KKK
B
A
+−−
−−−
−Δ++=
−−Δ+−
−
−
1
1
0
ˆ
ˆ
χ
(45)
and thus
() [] () [] ()
( )() ()
() () ()
() () () ()
()
snsdsBKsxsxCsBK
sBusuB
sxAsIsxAsI
y
B
A
+−−−
−Δ++=
−−Δ+−
ˆ
ˆ
0
χ
.(46)
Laplace transform of the observation error is thus
given by:
(
)
(
)
[]
() [] ()
()
[] ()
()
[] () () ()
()
snsdsBKCsBKAsI
suCsBKAsI
sxCsBKAsI
CsBKAsIs
y
B
A
++−−
Δ+−+
Δ+−+
+−=
−
−
−
−
1
1
1
0
1
χχ
(47)
4.2 Crone Observer Synthesis
Relation (47) demonstrates that without disturbances
and plant perturbations (
0=Δ
A
, 0
=
Δ
B
,
() ()
0=+ snsd
y
) observation error converges
exponentially to 0 if the roots of the determinant of
transfer matrix
() []
1−
+− CsBKAsI lie in the left
half complex plane, or equivalently given comments
before theorem 1, if the closed loop in Fig. 2 is
internally stable.
Moreover, relation (47) demonstrates that with
disturbances and plant perturbations, observation
errors can be reduced by finding a controller K(s)
that minimizes the modulus of the elements of the
transfer matrix
(
)
[
]
A
CsBKAsI Δ+−
−1
and vectors
(
)
[
]
B
CsBKAsI Δ+−
−1
and
(
)
[
]
(
) sBKCsBKAsI
1−
+−
. Also notes that final value
theorem can be applied on the elements on the
previous matrix and vectors, to analyse the effects of
plant perturbation and disturbances on observation
error.
CRONE observer synthesis thus consist in finding
an optimal open loop behaviour defined by
transmittance (25) that minimises the maximal gain
of matrix
(
)
[
]
A
CjBKAIj Δ+−
−1
ωω and vectors
(
)
[
]
B
CjBKAIj Δ+−
−1
ωω
and
(
)
[
]
(
)
ωωω jBKCjBKAIj
1−
+− as ω varies within
the frequency range
]
[
∞
,..,0 .
An algorithm for the CRONE observer synthesis can
thus be summarized as follows:
-
choice of an open-loop gain-crossover
frequency
ω
cg
that ensures a satisfactory
observation error cancellation dynamics;
-
choice of orders n
l
and n
h
in order to ensure that
the gain of the elements of matrix
(
)
[
]
A
CjBKAIj Δ+−
−1
ωω and vectors
(
)
[
]
B
CjBKAIj Δ+−
−1
ωω and
(
)
[
] ()
ωωω jBKCjBKAIj
1−
+− tends towards 0
as
ω tends towards 0 and infinity to ensure a
cancellation of observation error in steady stage
and an immunity of this error to measurement
noise;
-
optimisation of parameters of open loop
transmittance (25) through the minimisation of
the criterion
(
)
(
)()
[
]
∞
= ωωω jFjFjFJ
321
, (48)
with
(
)
(
)()
[
]
AA
CjBKAIjWjF Δ+−=
−1
1
ωωωω
(
)
(
)()
[
]
BB
CjBKAIjWjF Δ+−=
−1
2
ωωωω
(
)
(
)()
[
] ()
ωωωωω jBKCjBKAIjWjF
C
1
3
−
+−= ,
where
(
)
ω
A
W ,
(
)
ω
B
W and
()
ω
C
W denotes
weighting matrices;
-
synthesis of the controller K(s) using the
procedure described at the end of section 3.3
(relations (34) and (35)).
CRONE OBSERVER - Definition and Design Methodology
427

5 CONCLUSION
The main contribution of this paper is the
development of a dynamic output feedback based
observer that will be referred to as a CRONE
observer in future developments. This name results
in the introduction of CRONE controller in a
feedback loop whose goal is to cancel the error
between a model state and the unmeasured state of a
plant that must be estimated. State observation with
a dynamic output feedback based observer is
concept that was developed in two papers (Marquez,
2003) and (Marquez and Riaz, 2005). Such an
approach of state observation permits:
-
a generalisation of the Luenberger form
(Luenberger, 1971) that thus allows more
freedom and flexibility in the design,
-
a formulation allowing a more transparent view
of the observer properties in term of feedback
elements
-
to poses the disturbances rejection problem and
the observation robustness problem in the
context of robust control theory.
The main differences between this paper and
(Marquez, 2003) and (Marquez and Riaz, 2005) are :
-
the extension of the dynamic output feedback
based observer idea to the observation problem
with unknown input,
-
the uses of a CRONE controller to solve the
disturbances rejection problem and the
observation robustness (robustness of the
observation error convergence to zero).
With the CRONE controller, plant model
perturbations are taken into account in a structured
form with no overestimation (but unmodelled
dynamics can also be taken into account). Thus,
without conservatism introduced in the plant
uncertainties modelling, and in spite of a global
optimization proof lack of the non convex
optimisation problem defined in CRONE control, it
turn out that in practice a CRONE controller permits
to obtain better performance than an H
∞
one on the
same plants (see for instance (Landau, et al, 1995)
for a comparison on a benchmark based on robust
digital control of a flexible transmission system).
Due to the introduction of fractional differentiation,
a parameterization of the open loop transfer function
with a small number of parameters (three just like a
PID controller) is obtained. The optimisation of the
control law is thus reduced to the search for the
optimal values of these parameters.
REFERENCES
Biorci G. and S. Ridella (1970). Ladder RC network with
constant RC product -
IEEE Trans. Circuit Theory, 17.
Dutta Roy S. C. (1970). On the realization of a constant-
argument impedance of fractional operation - IEEE
Trans. Circuit Theory
, 17.
Hartley T. and C. Lorenzo (2005). Conjugated-order
Differ Integrals, ASME Conference, Long Beach,
California, 2005
Ichise M., Y. Nagayanagi and T. Kojima (1971). An
analog simulation of non integer order transfer
functions for analysis of electrode processes - J.
Electroanal. Chem. Interfacial Electrochem.
, 33, 253.
Landau I.D., Rey D., Karimi A., Voda A. and Franco A.,
(1995).
A Flexible Transmission System as a
Benchmark for Robust Digital Control
, European
Journal of Control, Vol. 1, pp. 77-96.
Lanusse P., A. Oustaloup and B. Mathieu (2000). Robust
control of LTI square MIMO plants using two
CRONE control design approaches - IFAC Symposium
on Robust Control Design "ROCOND 2000"
, Prague,
Czech Republic, June 21-23.
Luenberger D. G. (1971). An introduction to observers.
IEEE transactions on Automatic control, AC-16, 596-
602.
Marquez H. J. (2003). A frequency domain approach to
state estimation, Journal of the Franklin Institute, vol.
340, pp 147-157.
Marquez H. J., M. Riaz (2005). Robust state observer
design with application to an industrial boiler system,
Control Engineering Practice, n° 13, pp 713-728.
Miller K. S. and B. Ross (1993). An introduction to the
fractional calculus and fractional differential equations
-
John Wiley & Sons Inc., New York.
Oldham K. B. (1973). Semiintegral electroanalysis: analog
implementation , Anal. Chem., Vol. 45, p 39.
Oldham K. B. and J. Spanier (1974). The fractional
calculus, Academic Press, New York.
Oustaloup A. (1975). Etude et réalisation d'un système
d'asservissement d'ordre 3/2 de la fréquence d'un laser
à colorant continu -
PhD Thesis, Bordeaux I
University, France.
Oustaloup A., A. Ballouk, P. Melchior, P. Lanusse and A.
Elyagoubi (1990). Un nouveau régulateur CRONE
fondé sur la dérivation non entiere complexe -
GR
Automatique CNRS Meeting
, Bordeaux, France, March
29-30.
Oustaloup A. (1991). The CRONE control,
ECC'91 -
Grenoble, France, July 2-5.
Oustaloup A., B. Mathieu and P. Lanusse (1995). The
CRONE control of resonant plants: application to a
flexible transmission - European Journal of Control,
Vol. 1 n°2.
Oustaloup A., F. Levron, F. Nanot and B. Mathieu (2000).
Frequency-band complex non integer differentiator:
characterization and synthesis, IEEE Transactions on
Circuits and Systems,
Vol 47, n° 1, pp 25-40.
Pommier V., J. Sabatier, P. Lanusse, A. Oustaloup (2002).
CRONE control of a nonlinear Hydraulic Actuator -
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
428

Control Engineering Practice, Vol. 10, n°4, pp. 391-
402
Sabatier J., Poullain S., Latteux P., Thomas J. L.,
Oustaloup A. (2004),
Robust speed control of a low
damped electromechanical system: application to a
four mass experimental test bench
, International
Journal of Nonlinear Dynamics and Chaos in
Engineering Systems, Vol. 38, n° 1-4, pp 383-400.
Samko S. G., A. A. Kilbas and O. I. Marichev (1993).
Fractional integrals and derivatives - Gordon and
Breach Science Publishers
.
Suezaki and Takahashi (1966). Phase splitter of symmetric
lattice network type and the termination with the
impedance 1/
s
- Paper of the technical group on
network and system theory, IECE
, Japan, 1966.
CRONE OBSERVER - Definition and Design Methodology
429