ROBUST ADAPTIVE CONTROL USING A FRACTIONAL
FEEDFORWARD BASED ON SPR CONDITION
Samir Ladaci, Jean Jacques Loiseau
IRCCyN, Ecole Centrale de Nantes, 1, rue de la No
¨
e, BP: 92101 Nantes, 44321, France
Abdelfatah Charef
D
´
epartement d’Electronique, Universit
´
e Mentouri, Route de Ain Elbey, Constantine 25000, Algeria
Keywords:
Robust adaptive control, Fractional Adaptive Control, Model Reference Adaptive Control, Feedforward, Frac-
tional order systems.
Abstract:
This paper presents a new approach for robust adaptive control, using fractional order systems as parallel
feedforward in the adaptation loop. The basic adaptive algorithm used here is Model Reference Adaptive
Control (MRAC), which do not require explicit parameter identification. The problem is that such a control
system may diverge when confronted with finite sensor and actuator dynamics, or with parasitic disturbances.
One of the classical robust adaptive control solutions to these problems, makes use of parallel feedforward and
simplified adaptive controllers based on the concept of positive realness.
This control scheme is based on the ASPR property of the plant. We show that this condition implies also
robust stability in case of fractional order controllers. A simulation example of a SISO robust adaptive control
system illustrates the interest of the proposed method in the presence of disturbances and noises.
1 INTRODUCTION
Adaptive control has proven to be a good control so-
lution for the partially unknown systems or varying
parameter systems. In this domain Model reference
adaptive control (MRAC) became very popular since
it presents a very simple algorithm with easy im-
plementation and does not require identifiers or ob-
servers in the control loop (Astrom and Wittenmark,
1995; Landau, 1979). However such algorithm shows
its limits in noisy or disturbed environment, which
may make it inefficient or uncompetitive. Unfortu-
nately very few industrial control processes are not
subject to theses practical problems, which can dam-
age the quality of product and the good process oper-
ating.
The use of simple parallel feedforward in the adap-
tation loop appeared as a robust solution since the
80’s. Many works have used this approach towards
robust control systems (Bar-Kana, 1987; Naceri and
Abida, 2003). In the last decade a great interest was
given to fractional order systems, which have shown
good robustness performances, several robust control
methods based on these systems have been developed,
like CRONE Control (Oustaloup, 1991) and frac-
tional adaptive control (Vinagre et al., 2002; Ladaci
and Charef, 2006; Ladaci et al., 2007).
In this paper we present a fractional robust adaptive
control solution for disturbed applications, based on
the idea of Bar-kana (Bar-Kana, 1987), which uses the
basic stabilizability property of the plant and simple
parallel feedforward in order to satisfy the desired ”al-
most positive realness” condition that can guarantee
robust stability of the nonlinear adaptive controller.
The main contribution of this work is to improve the
feedforward approach robust performances by using
fractional order filters. This result is illustrated by a
simulation example of a test in bad realistic condi-
tions like finite bandwidth of actuators, input and out-
put disturbances and no assumed natural damping.
This paper is structured as follows:
In section 2 definitions of fractional order systems are
presented. Section 3 introduces the principles of ro-
bust adaptive control based on the concept of ’pos-
itive realness’ condition and then the main result in
fractional order case is presented in section 4. The
implementation in Model Reference Adaptive Con-
trol scheme is introduced in section 5 and a simulation
414
Ladaci S., Jacques Loiseau J. and Charef A. (2007).
ROBUST ADAPTIVE CONTROL USING A FRACTIONAL FEEDFORWARD BASED ON SPR CONDITION.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 414-420
DOI: 10.5220/0001636904140420
Copyright
c
 SciTePress

example is given in section 6. The paper is concluded
in section 7.
2 FRACTIONAL ORDER
SYSTEMS
The analysis in Bode plot of many natural pro-
cesses, like transmission lines, dielectric polarisation
impedance, interfaces, cardiac rhythm, spectral den-
sity of physical wave, some types of noise (Van-
DerZiel, 1950; Duta and Hom, 1981), has allowed
to observe a fractional slope. This type of process
is known as 1/ f process or fractional order system.
During the last decade, a great interest was given by
researchers to the study of these systems (Sun and
Charef, 1990) and their application in control systems
(Oustaloup, 1991; Hotzel and Fliess, 1997; Ladaci
and Charef, 2006; Ladaci et al., 2007).
A SISO fractional order system can be represented by
the following transfer function,
X(s) =
b
m
s
β
m
+ b
m−1
s
β
m−1
+ ...+ b
0
s
β
0
a
n
s
α
n
+ a
n−1
s
α
n−1
+ ... + a
0
s
α
0
(1)
Where,
• α
i
, β
j
: real numbers such that,

0 ≤ α
0
< α
1
< ... < α
n
0 ≤ β
0
< β
1
< ... < β
m
• s: Laplace operator.
for the purpose of this work, let us introduce the fol-
lowing definitions,
Definition 1 The fractional order transfer function
X(s) given in (1) is called proper if: β
m
≤ α
n
It is called stricly proper if: β
m
< α
n
Definition 2 (Desoer and Vidyasagar, 1975) The
fractional order transfer function Matrix M
X
(s)
whose elements are of the form (1) is proper (strictly
proper) if and only if all elements of M
X
(s) are
bounded at ∞ (tend to zero at ∞, resp.).
We use in the sequel a description equation into
frequency domain of a single pole fractional order
process, given as follows:
Y(s) =
1
(s+ p
T
)
α
(2)
with
• α: fractional exponent, 0 ≤ α ≤ 1
• p
T
: fractional pole which is the cut frequency.
Many previous works have shown that fractional
systems present best qualities, in response time and in
transition dynamic stability (Sun and Charef, 1990).
All the control theory developed by Oustaloup es-
pecially on CRONE control was based on fractional
order systems robustness in presence of uncertainties
and perturbations (Oustaloup, 1991).
3 CONCEPT OF POSITIVE
REALNESS CONDITION
Robustness is defined relatively to a certain property
and a set of models. A property (generally stability
or performance level) is said to be robust if all
the models belonging to the set satisfy it. Robust
adaptive stabilization means that all values involved
in the adaptation process namely, states, gains and
errors are bounded in the presence of any bounded
input commands and input or output disturbances
(Bar-Kana and Kaufman, 1985; Kwan et al., 2001).
In this paper we are interested by a particular con-
figuration of feedforward controllers combined with
MRAC control and fractional order systems giving a
fractional robust adaptive control method.
The use of a simple feedforward in the adaptation
loop (see Figure 4) improves the robust stability of the
control system. This approach is based on the con-
cept of the ”positive realness” condition (Bar-Kana,
1989); witch can guarantee stable implementation of
adaptive control configuration. Let us present these
definitions:
Definition 3 The m × m transfer function matrix
G
s
(s) is called strictly positive real (SPR) if (Landau,
1979; Bar-Kana, 1989):
1. All elements of G
s
(s) are analytic in ℜ(s) ≥ 0.
2. G
s
(s) is real for real s.
3. G
s
(s) + G
T∗
s
(s) > 0 for ℜ(s) ≥ 0 and finite s.
We also show that (Shaked, 1977) for a fractional or-
der transfer function matrix G
s
(s),
G
s
(s) is SPR ⇔ G
−1
s
(s) is SPR (3)
Indeed, by using the SPR property if we write (Bar-
Kana, 1989),
G
s
(s) = A+ jB ⇒ G
T∗
s
(s) = A
T
− jB
T
Since by definition
G
s
(s) + G
T∗
s
(s) = A+ A
T
+ j(B− B
T
) > 0
ROBUST ADAPTIVE CONTROL USING A FRACTIONAL FEEDFORWARD BASED ON SPR CONDITION
415

we get B = B
T
and A > 0 (not necessary symmetric).
Then whenever
ℜ[G
s
(s)] = A > 0
we get
G
−1
s
(s) = (A+ BA
−1
B
T
)
−1
− jA
−1
B(A+ BA
−1
B
T
)
−1
and
ℜ

G
−1
s
(s)

= (A+ BA
−1
B
T
)
−1
> 0
which proves (3).
Definition 4 (Bar-Kana, 1987)
Let G
a
(s) be a m× m transfer matrix. Let us assume
that there exists a positive definite constant gain ma-
trix,
˜
K
e
such that the closed-loop transfer function
G
c
(s) =

I + G
a
(s)
˜
K
e

−1
G
a
(s) (4)
is SPR. G
a
(s) is called ”almost strictly positive real
(ASPR)”.
Now if we consider a fractional order proper or
strictly proper ASPR transfer matrix G
s
(s).
Then the following statements are equivalent,
G
s
(s) = [I + G
a
(s)K
e
]
−1
G
a
(s) is SPR (5)
G
s
(s) = [I + G
a
(s)K
e
]
−1
is SPR (6)
G
−1
s
(s) = G
−1
a
(s) + K
e
is SPR (7)
ℜ

G
−1
a
(s) + K
e

ℜ(s)≥0
> 0 (8)
G
−1
s
(s) is asymptotically stable and
K
e
is sufficiently large (9)
Because ∃M such that ℜ

G
−1
a
(s)

ℜ(s)≥0
> M > −∞,
and then any K
e
> −M will do (Bar-Kana, 1989).
G
a
(s) is strictly minimum phase and
K
e
is sufficiently large (10)
All the above algebraic manipulation, as done to
obtain (3) and definitions 3 and 4, apply to fractional
systems as well. Here we can generalize as fellows
the result of (Bar-Kana, 1989) to the fractional order
case.
Lemma 1 Let a fractional order transfer function
matrix G
a
(s) be ASPR and let
˜
K
e
be any gain that
satisfies (4). Then G
a
(s) is SPR for any gain K
e
that
satisfies K
e
>
˜
K
e
.
It is obvious that ASPR fractional order systems,
which are minimum phase proper systems maintain
stability with high gains. The high gain stability is
important when nonstationary or nonlinear (adaptive)
control is used, because the robustness of the control
system is maintained if, due to specific operational
conditions, the time-varying gains become too large.
Remarks
1. The ASPR plant must also be proper.
2. The open loop is not necessarily stable (the plant
will actually be stabilized by the fictitious gain
K
e
), however all the zeros must be placed in the
left half plane. The plant must be minimum phase
to obtain positivity.
3. We can easily show (Bar-Kana, 1987) that if a sys-
tem is ASPR, then it can be stabilized by any con-
stant or time variable output gain K
e
, if it is large
enough, i.e. K
e
>
˜
K
e
.
But in this method, instead of using high gain regula-
tion we will use a simple parallel feedforward config-
uration which can by a similar way satisfy the positive
realness conditions.
The idea of using feedforward in parallel with the
controlled plant is based on the following Lemma of
Bar-Kana,
Lemma 2 (Bar-Kana, 1989) Let the plant be de-
scribed by the m× m transfer function G
p
(s) of order
n. Let C(s) be any dynamic stability output feedback
controller. Then
G
a
(s) = G
p
(s) +C
−1
(s) (11)
is ASPR if C
−1
(s) is proper or strictly proper.
We can adapt the proof of (Bar-Kana, 1989; Bar-
Kana, 1986)) to the fractional case.
4 MAIN RESULT
At this stage we propose a fractional order feedfor-
ward configuration of the form:
F(s) =
F
p

1+
s
s
0

α
(12)
with a real fractional power 0 < α < 1, to improve the
robustness of the adaptive algorithm, in presence of
perturbations, as such systems do not amplify much
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
416

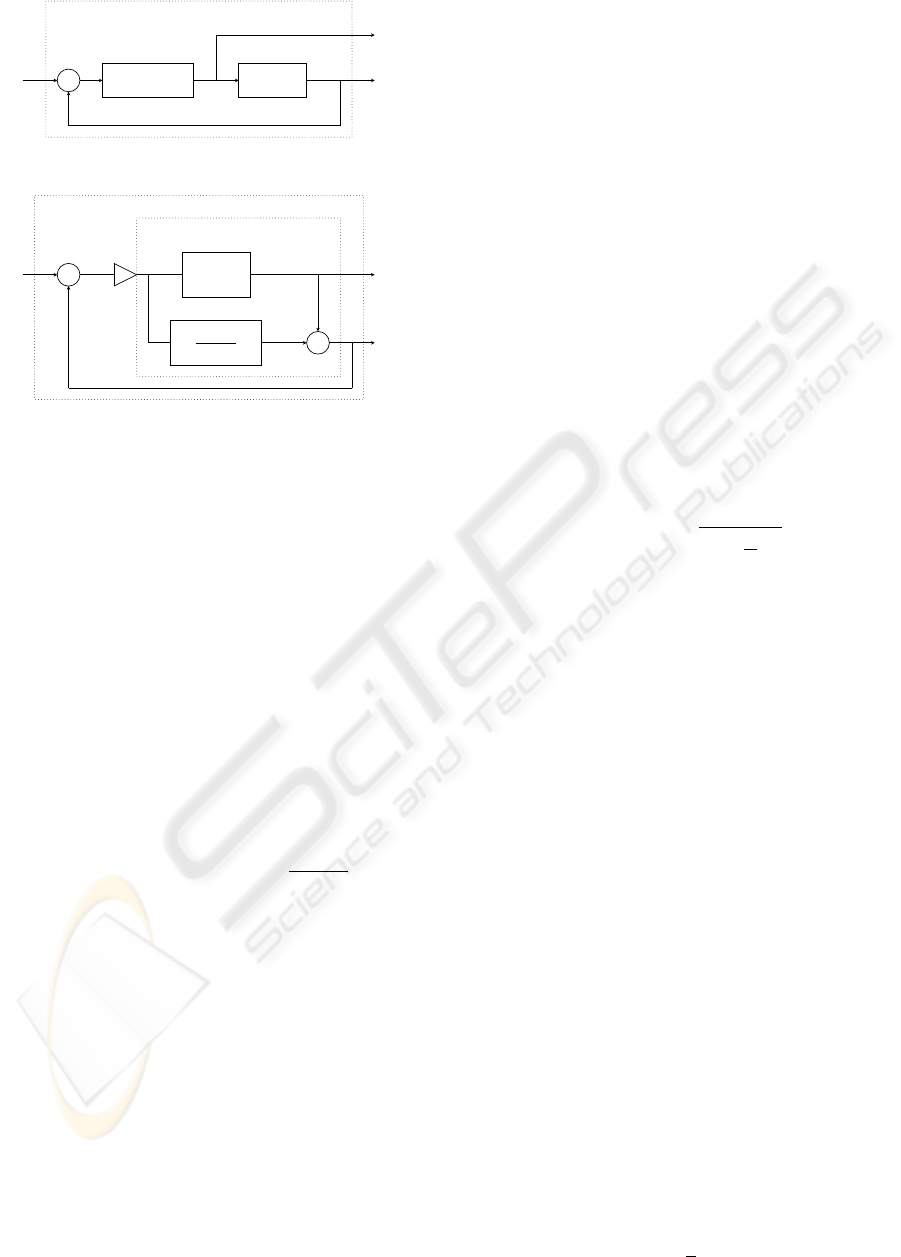
G(s)K(1+ qs
α
)
u(s)
y(s)
G
CL
(s)
u
c
(s)
−
+
Figure 1: Closed-loop system.
G(s)
K
−1
1+qs
α
y
s
(s)
y
a
(s)
y
p
(s)
G
a
(s)
G
s
(s)
K
e
u
c
(s)
+
−
Figure 2: The fictitious SPR configuration.
these random signals. This configuration could be
considered as the inverse of an improper fractional
PD
µ
controller, which was used in control systems
with good proven performances (Oustaloup, 1983;
Hotzel and Fliess, 1997; Podlubny, 1999).
We can formulate the main result of this paper in the
following theorem.
Theorem 1 Let G(s) be any m × m strictly proper
transfer matrix of arbitrary MacMillan degree. G(s)
is not necessarily stable or minimum phase. Let
H
f
(s) = K(1+ qs
α
) (13)
be some stabilizing controller for G(s). Then the aug-
mented controlled plant
G
f
a
(s) = G(s) + H
−1
f
(s) = G(s) +
K
−1
1+ qs
α
(14)
is ASPR.
Proof of Theorem 1:
From definition 4, if G
a
(s) is ASPR then the closed-
loop transfer function
G
c
(s) =

I + G
a
(s)
˜
K
e

−1
G
a
(s)
is ASPR.
Since H
−1
f
(s) from (13) is strictly proper (relative
degree α > 0), then Lemma 2 implies that the
augmented system G
f
a
(s) as defined in (14) is ASPR,
which proves Theorem 1.
The stabilizing controller H
f
(s) can also be mod-
elized as follows,
H
f
(s) = K(1+ qs)
α
(15)
Figure 1 represents the feedback control system cor-
responding to the control (13).
From Definition 4 and the fact that the transfer func-
tion G
f
a
(s) is ASPR, we know that it can be stabilized
by a gain
˜
K
e
. Figure 2 illustrates the feedforward con-
figuration. In addition, the stabilization is robust, it
holds for any gain K
e
>
˜
K
e
.
Many previous works (Hotzel and Fliess, 1997;
Podlubny, 1999) have proposed PD
µ
improper con-
trollers of the form (13):
C(s) = K
p
+ K
i
s
α
(16)
which can stabilize many realistic plants for sufficient
high values of K.
A feedforward of equivalent effect is chosen as fol-
lows:
F(s) = C
−1
(s) =
F
p

1+
s
s
0

α
(17)
Where F
p
= K
−1
, such that the augmented plant be-
comes:
G
a
(s) = G
p
(s) + F(s) (18)
As K should be very large, so F
p
are small coeffi-
cients, guaranteeing that G
a
(s) be ASPR. And dur-
ing the control design we can take G
a
(s) ≈ G
p
(s) as a
practical approximation.
5 IMPLEMENTATION IN MRAC
SCHEME
Model Reference Adaptive Control (MRAC) is one
of the more used approaches of adaptive control, in
which the desired performance is specified by the
choice of a reference model. Adjustment of param-
eters is achieved by means of the error between the
output of the plant and the model reference output.
Let us introduce the basic ideas of this approach rep-
resented in Figure 3.
We consider a closed loop system where the con-
troller has an adjustable parameter vector θ. A model
which output is y
m
specifies the desired closed loop
response. Let e be the error between the closed loop
system output y and the model one y
m
, one possibility
is to adjust the parameters such that the cost function:
J(θ) =
1
2
e
2
(19)
ROBUST ADAPTIVE CONTROL USING A FRACTIONAL FEEDFORWARD BASED ON SPR CONDITION
417

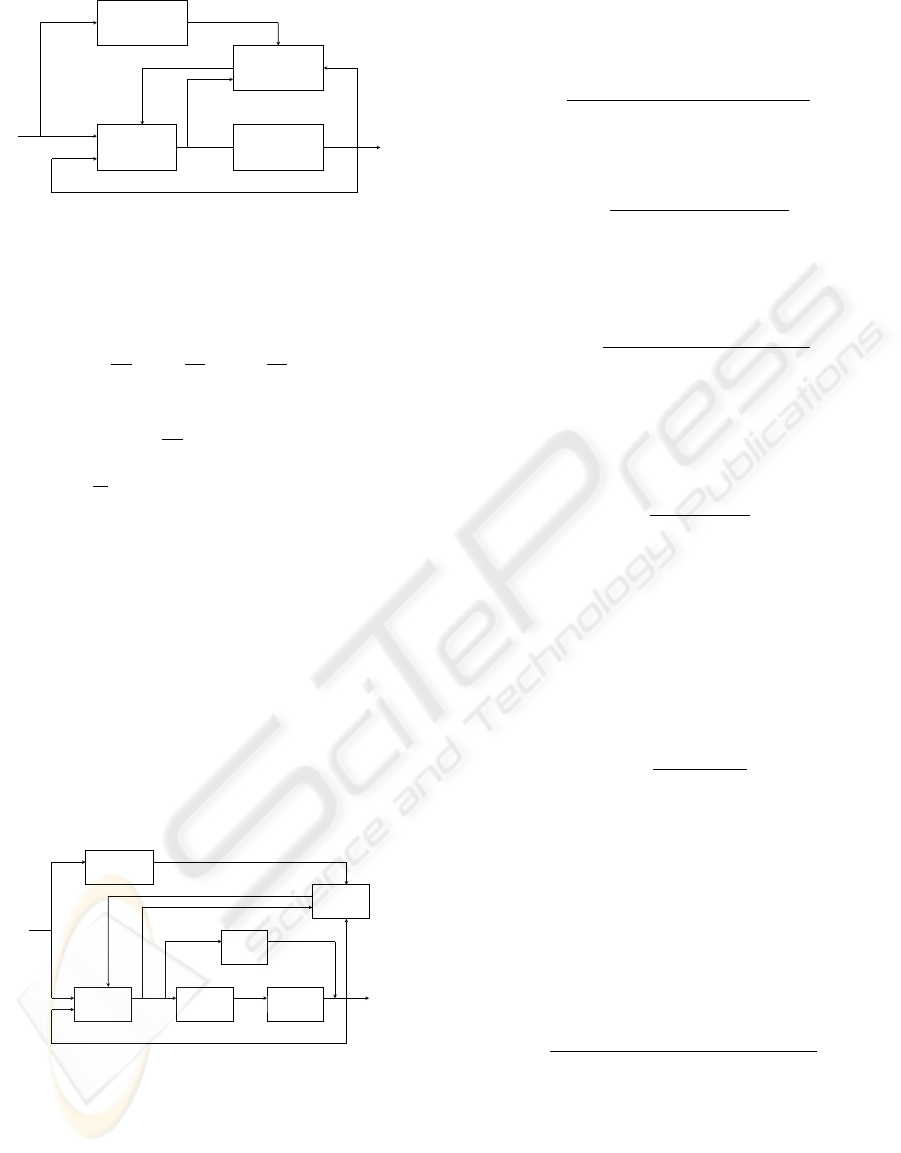
y
m
u
y
u
c
Adjustment
Mechanism
Process
Controller
Reference
Model
Parameters of the Controller
Figure 3: Direct Model Reference Adaptive Control.
be minimised. In order to make J small it is reason-
able to change parameters in the direction of negative
gradient J, so:
dθ
dt
= −γ
δJ
δθ
= −γe
δe
δθ
(20)
or
dθ
dt
= γϕe (21)
where ϕ = −
δe
δθ
is the regression (or measures) vector
and γ is the adaptation gain. This aproach is called
M.I.T. rule.
The introduction of a simple feedforward in the
MRAC adaptation loop us represented in figure 4
improves the robust stability performance against
the controller gain fluctuations in presence of per-
turbation and noises (Naceri and Abida, 2003).
Previous works (Sobel and Kaufman, 1986), showed
that the ASPR property of a process, allows the
implementation of very simple adaptive controllers
that garantee robust stability of the closed loop in
presence of bounded input or output disturbances.
The feedforward transfer function is choosen like in
(12) where the gain F
p
is a small coefficient.
F
ProcessActuator
Controller
u
c
y
m
Reference
Model
Adjustment
Mechanism
y
u
Figure 4: Simple feedforward in MRAC scheme.
6 SIMULATION EXAMPLE
Without any loss of generality we will apply this ro-
bust adaptive control method, both in the case of inte-
ger and fractional order feedforward, to a SISO model
of a DC motor controlled in respect of velocity, given
by:
G
p
(z) =
0.8513z+ 5.099 10
−6
z
2
+ 2.442 10
−7
z+ 1.37 10
−11
(22)
with a sampling period T
s
= 0.3sec, and an actuator
model of the form:
A(z) =
0.007667z+ 0.007049
z
2
− 1.763z+ 0.7772
(23)
The plant is subject to random input and output per-
turbations of amplitudes 2 and 0.05 respectively.
The reference model G
m
is given by:
G
m
(z) =
0.9411z+ 0.1208
z
2
+ 0.05679z+ 0.005092
(24)
6.1 Integer Order Feedforward Case
The feedforward trunsfer fuction F is given by:
F(z) =
3.2394 10
−7
z− 0.9997
(25)
with a regulation parameter γ = 0.001 we obtain the
results of Figure 5.
6.2 Fractional Order Feedforward Case
The fractional order feedforward trunsfer function F
is given in Laplace domain by:
F(s) =
0.001
(s+ 500)
0.6
(26)
For the purpose of our approach we need to use an
integer order model approximation of the fractional
order feedforward model in order to implement the
adaptation algorithm, for this aim we have used the
so-called singularity function method (Charef et al.,
1992).
The fractional transfer function (26) is approximated
to a linear transfer function and sampled to give the
following formula:
ˆ
F(z) =
0.001(z− 4.78 10
−97
)
z
2
− 2.407 10
−96
z+ 1.001 10
−207
(27)
with a regulation parameter γ = 0.005, we obtain the
results of Figure 6.
6.3 Remarks
• The command signal u is more polish in the frac-
tional case witch is a very useful property in reg-
ulation problem.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
418

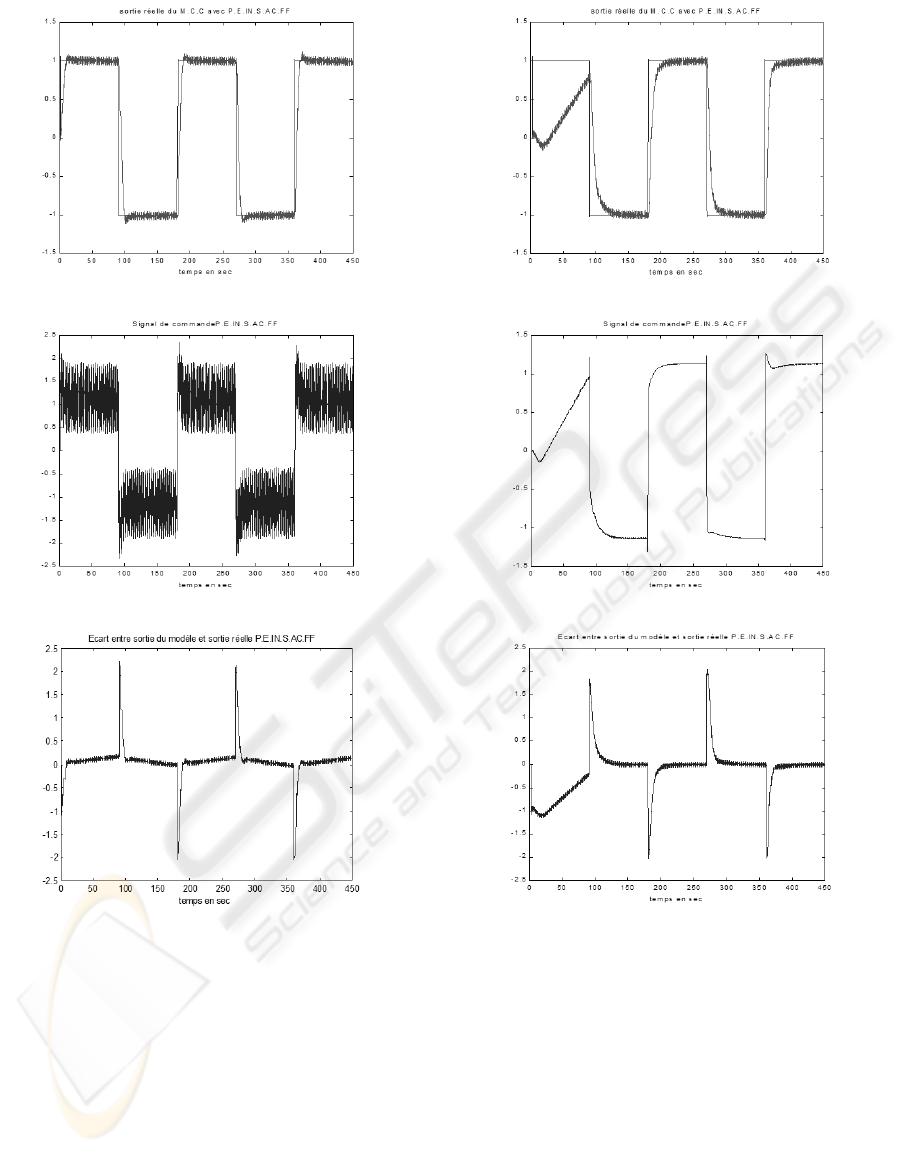
(a)
(b)
(c)
Figure 5: Process output with integer feedforward
(a) Process output y(t), (b) Control signal u(t), (c) Error
signal e(t).
• The proposed fractional order configuration of
feedforward maintains stability and at less the
same level of performances, witch confirms the
interest of integrating fractional strategy in robust
adaptive control.
(a)
(b)
(c)
Figure 6: Process output with fractional feedforward
(a) Process output y(t), (b) Control signal u(t), (c) Error
signal e(t).
7 CONCLUSION
In this paper we have presented a new robust adap-
tive control strategy, by introducing simple fractional
feedforward configuration in the MRAC algorithm.
The concept of positive realness condition which is
the basis of this robust control strategy is extended to
fractional order control systems. The idea was to take
benefit of the high performance quality of fractional
ROBUST ADAPTIVE CONTROL USING A FRACTIONAL FEEDFORWARD BASED ON SPR CONDITION
419

order systems confirmed in many precedent research
works. The stability proofs of this adaptive control
scheme developed for integer order filters in control
literature still holds for such systems. Simulation re-
sults have shown a better filtering ability of command
and output signals, and more robustness against ad-
ditive perturbations, than in the integer order feedfor-
ward configuration case.
REFERENCES
Astrom, K. and Wittenmark, B. (1995). Adaptive Control.
Addison-Wesley, USA.
Bar-Kana, I. (1986). Positive realness in discrete-time adap-
tive control systems. International Journal of Systems
Science, 17(7):1001–1006.
Bar-Kana, I. (1987). Parallel feedforward and simplified
adaptive control. Int. J. Adaptive Control and Signal
Processing, 1(2):95–109.
Bar-Kana, I. (1989). On positive realness in multivariable
stationary linear systems. In Conference on Infor-
mation Sciences and Systems, Baltimore, Maryland,
USA.
Bar-Kana, I. and Kaufman, H. (1985). Global stability and
performance of a simplified adaptive algorithm. Int. J.
Control, 42(6):1491–1505.
Charef, A., Sun, H., Tsao, Y., and Onaral, B. (1992). Fractal
system as represented by singularity function. IEEE
Trans. On Automatic Control, 37:1465–1470.
Desoer, C. and Vidyasagar, M. (1975). Feedback Systems:
Input-Output Properties. Academic Press, N.Y. USA.
Duta, P. and Hom, P. (1981). Low frequency fluctuations in
solids: 1/f noise. Review of modern physics, 53(3).
Hotzel, R. and Fliess, M. (1997). Syst
`
emes lin
´
eaires frac-
tionnaires avec et sans retard : Stabilit
´
e, commande,
exemples. In Actes d’AGIS’97, pages 53–58, Angers.
Kwan, C., Dawson, D., and Lewis, F. (2001). Robust adap-
tive control of robots using neural network: Global
stability. Asian Journal of Control, 3(2):111–121.
Ladaci, S. and Charef, A. (2006). On fractional adaptive
control. Nonlinear Dynamics, 43:365–378.
Ladaci, S., Loiseau, J., and Charef, A. (2007). Fractional
order adaptive high-gain controllers for a class of lin-
ear systems. Communications in Nonlinear Science
and Numerical Simulations. Elsevier, In Press.
Landau, Y. (1979). Adaptive Control : The model reference
Approach. Marcel Dekker, New York.
Naceri, F. and Abida, L. (2003). A novel robust adaptive
control algorithm for ac drives. Computers and Elec-
trical Engineering.
Oustaloup, A. (1983). Systmes asservis d’ordre fraction-
naire. Masson, Paris.
Oustaloup, A. (1991). La commande CRONE. Herm
`
es,
Paris.
Podlubny, I. (1999). Fractional order systems and pi
λ
d
µ
controllers. IEEE Transactions on Automatic Control,
44(1):208–214.
Shaked, U. (1977). The zero properties of linear passive
systems. IEEE Transactions on Automatic Control,
22(6):973–976.
Sobel, K. and Kaufman, H. (1986). Direct model refer-
ence adaptive control for a class of mimo systems. in
C. Leondes (ed.) Control and Dynamic Systems- Ad-
vances in Theory and Applications, 24.
Sun, H. and Charef, A. (1990). Fractal system-a time do-
main approach. Annals of Biomedical Ing.
VanDerZiel, A. (1950). On the noise spectra of semicon-
ductor noise and of flikker effects. Physica.
Vinagre, B., Petras, I., and Chen, Y. (2002). Using fractional
order adjustment rules and fractional order reference
models in model-reference adaptive control. Nonlin-
ear Dynamics, 29:269–279.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
420