MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER
FOR THE ROBUST LOCALIZATION OF A MOBILE ROBOT
Y. Touati, Y. Amirat, Z. Djama and A. Ali Chérif*
LISSI Laboratory, Paris 12 University, 120-122 rue Paul Armangot
94400 Vitry-sur-Seine, France
*Department of Computing, University of Paris 8, 2 rue de la liberté - 93526 Saint-Denis cedex
Keywords: Mobile robot, Robust Localization, Multiple Model, Hybrid Systems, Kalman Filtering, Data Fusion.
Abstract: This paper focuses on robust pose estimation for mobile robot localization. The main idea of the approach
proposed here is to consider the localization process as a hybrid process which evolves according to a model
among a set of models with jumps between these models according to a Markov chain. In order to improve
the robustness of the localization process, an on line adaptive estimation approach of noise statistics (state
and observation), is applied for each mode. To demonstrate the validity of the proposed approach and to
show its effectiveness, we’ve compared it to the standard approaches. For this purpose, simulations were
carried out to analyze the performances of each approach in various scenarios.
1 INTRODUCTION
Localization constitutes a key problem in mobile
robotics (Borenstein, 1996). It consists of estimating
the robot’s pose (position, orientation) with respect
to its environment from sensor data. Therefore, a
better sensory data exploitation is required to
increase robot’s autonomy. The simplest way to
estimate the pose parameters is the integration of
odometric data which, however, is associated with
unbounded errors, resulting from uneven floors,
wheel slippage, limited resolution of encoders, etc.
However, such a technique is not reliable due to
cumulative errors occurring over the long run.
Therefore, a mobile robot must also be able to
localize or estimate its parameters with respect to the
internal world model by using the information
obtained with its external sensors.
The use of sensory data from a range of disparate
multiple sensors, is to automatically extract the
maximum amount of possible information about the
sensed environment under all operating conditions.
The main idea of data fusion methods is to provide a
reliable estimation of robot’s pose, taking into
account the advantages of the different sensors
(Harris, 1998). The Kalman filter is the best known
and most widely applied parameter and state
estimation algorithm in data fusion methods (Gao,
2002). Such a technique can be implemented from
the kinematic model of the robot and the observation
(or measurement) model, associated to external
sensors (gyroscope, camera, telemeter, etc.).
Basically, the Kalman filter gives a linear, unbiased,
and minimum error variance recursive algorithm to
optimally estimate the unknown state of a linear
dynamic system from Gaussian distributed noisy
observations. The Kalman filtering process can be
considered as a prediction-update formulation. The
algorithm uses a predefined linear model of the
system to predict the state at the next time step. The
prediction and updates are combined using the
Kalman gain which is computed to minimize the
Mean Square Error (MSE) of the state estimate. The
Extended Kalman Filter (EKF) is a version of the
Kalman filter that can handle non-linear dynamics or
non-linear measurement equations. Various
approaches based on EKF have been developed.
These approaches work well as long as the used
information can be described by simple statistics
well enough. The lack of relevant information is
compensated by using models of various processes.
However, such model-based approaches require
assumptions about parameters which might be very
difficult to determine (white Gaussian noise and
initial uncertainty over Gaussian distribution).
Assumptions that guarantee optimum convergence
are often violated and, therefore, the process is not
446
Touati Y., Amirat Y., Djama Z. and Ali Chérif A. (2007).
MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER FOR THE ROBUST LOCALIZATION OF A MOBILE ROBOT.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 446-454
DOI: 10.5220/0001633704460454
Copyright
c
 SciTePress

optimal or it can not even converge. In fact, many
approaches are based on fixed values of the
measurement and state noise covariance matrices.
However, such information is not a priori available,
especially if the trajectory of the robot is not
elementary and if changes occur in the environment.
Moreover, it has been demonstrated in the literature
that how poor knowledge of noise statistics (noise
covariance on state and measurement vectors) may
seriously degrade the Kalman filter performance
(Jetto, 1999). In the same manner, the filter
initialization, the signal-to-noise ratio, the state and
observation processes constitute critical parameters,
which may affect the filtering quality. The stochastic
Kalman filtering techniques were widely used in
localization (Gao, 2002) (Chui, 1987) (Arras,
2001)(Borthwick, 1993) (Jensfelt, 2001) (Neira,
1999) (Perez, 1999) (Borges, 2003). Such
approaches rely on approximative filtering, which
requires ad hoc tuning of stochastic modelling
parameters, such as covariance matrices, in order to
deal with the model approximation errors and bias
on the predicted pose. In order to compensate such
error sources, local iterations (Kleeman, 1992),
adaptive models (Jetto 1999) and covariance
intersection filtering (Julier, 1997)(Xu, 2001) have
been proposed. An interesting approach solution was
proposed in (Jetto, 1999), where observation of the
pose corrections is used for updating of the
covariance matrices. However, this approach seems
to be vulnerable to significant geometric
inconsistencies of the world models, since
inconsistent information can influence the estimated
covariance matrices.
In the literature, the localization problem is often
formulated by using a single model, from both state
and observation processes point of view. Such an
approach, introduces inevitably modelling errors
which degrade filtering performances, particularly,
when signal-to-noise ratio is low and noise variances
have been estimated poorly. Moreover, to optimize
the observation process, it is important to
characterize each external sensor not only from
statistic parameters estimation perspective but also
from robustness of observation process perspective.
It is then interesting to introduce an adequate model
for each observation area in order to reject unreliable
readings. In the same manner, a wrong observation
leads to a wrong estimation of the state vector and
consequently degrades the performance of
localization algorithm. Multiple-Model estimation
has received a great deal of attention in recent years
due to its distinctive power and great recent success
in handling problems with both structural and
parametric uncertainties and/or changes, and in
decomposing a complex problem into simpler sub-
problems, ranging from target tracking to process
control (Blom, 1988)(Li, 2000) (Li, 1993)(Mazor,
1996).
This paper focuses on robust pose estimation for
mobile robot localization. The main idea of the
approach proposed here is to consider the
localization process as a hybrid process which
evolves according to a model among a set of models
with jumps between these models according to a
Markov chain (Djama, 1999)(Djama, 2001). A close
approach for multiple model filtering is proposed in
(Oussalah 2001). In our approach, models refer here
to both state and observation processes. The data
fusion algorithm which is proposed is inspired by
the approach proposed in (Dufour 1994). We
generalized the latter for multi mode processes by
introducing multi mode observations. We also
introduced iterative and adaptive EKFs for
estimating noise statistics. Compared to a single
model-based approach, such an approach allows the
reduction of modelling errors and variables, an
optimal management of sensors and a better control
of observations in adequacy with the probabilistic
hypotheses associated to these observations. For this
purpose and in order to improve the robustness of
the localization process, an on line adaptive
estimation approach of noise statistics (state and
observation) proposed in (Jetto, 1999), is applied to
each mode. The data fusion is performed by using
Adaptive Linear Kalman Filters for linear processes
and Adaptive Extended Kalman Filters for nonlinear
processes.
The reminder of this article is organized as
follows. Section 2 discusses the problem statement
of multi-sensor data fusion for the localization of a
mobile robot. We develop the proposed robust pose
estimation algorithm in section 3 and its application
is demonstrated in section 4. Experimental results
and a comparative analysis with standard existing
approaches are also presented in this section.
2 PROBLEM STATEMENT
This paper deals with the problem of multi sensor
filtering and data fusion for the robust localization of
a mobile robot. In our present study, we consider a
robot equipped with two telemeters placed
perpendicularly, for absolute position measurements
of the robot with respect to its environment, a
gyroscope for measuring robot’s orientation, two
drive wheels and two separate encoder wheels
MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER FOR THE ROBUST LOCALIZATION OF A
MOBILE ROBOT
447

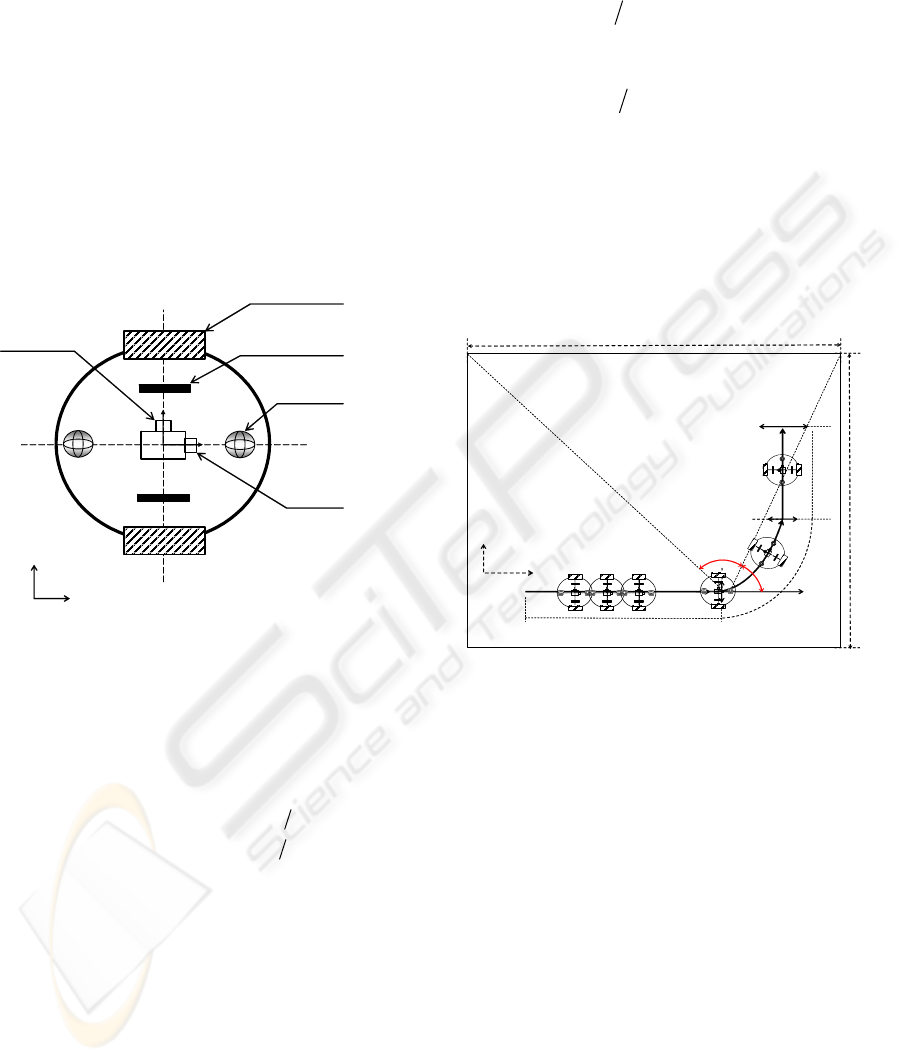
attached with optical shaft encoders for odometry
measurements (Figure 1). The environment where
the mobile robot moves is a rectangular room
without obstacles (Figure 2). The aim is not to
develop a new method for environment
reconstruction or modelling from data sensors;
rather, the goal is to propose a new approach to
improve existing data fusion and filtering techniques
for robust localization of a mobile robot. For an
environment with a more complex shape, the
observation model, which has to be employed at a
given time, will depend on the robot’s situation
(robot’s trajectory, robot’s pose with respect to its
environment) and on the geometric or symbolic
model of environmen
t.
Drive-wheel
Encoder -wheel
Balancing-wheel
Telemeter with respect
to X-axis
Telemeter with respect
to Y-axis
x
’
y’
x
y
Figure 1: Mobile robot description.
Odometric model: Let
(
) []
T
e
kkykxkX )()()( θ =
be
the state vector at time
k , describing the robot’s
pose with respect to the fixed coordinate system.
The kinematic model of the robot is described by the
following equations:
(
) 2cos
1 kkkkk
lxx θθ Δ+⋅+=
+
(1)
(
) 2sin
1 kkkkk
lyy θθ Δ++=
+
(2)
kkk
θθθ Δ+=
+1
(3)
with: 2/)(
l
k
r
kk
lll += and dll
l
k
r
kk
/)( −=Δ θ .
r
k
l
and
l
k
l are the elementary displacements of the right
and the left wheels;
d the distance between the two
encoder wheels.
Observation model of telemeters: As the
environment is a rectangular room, the telemeters
measurements correspond to the distances from the
robot location to walls (Fig. 2.).
Then, the observation model of telemeters
is described as follows:
for
(
)
l
k θθ <≤0 :
(
)
(
)
(
)
(
)
(
) kkxdkd
x
θ cos−=
with respect to
X
axis
(4)
for
(
)
ml
k θθθ ≤≤
:
(
)
(
)
(
)
(
) kkydkd
y
θ sin)( −= with respect to
Y axis.
(5)
with:
-
x
d and
y
d , respectively the length and the width of
the experimental site;
-
l
θ and
m
θ , respectively the angular bounds of
observation domain with respect to
X and Y axes;
-
(
) kd is the distance between the robot and the
observed wall with respect to
X or Y axes at time k .
X
Y
T
1
T
2
T
3
θ
l
θ
m
d
y
d
x
Figure 2: Telemeters measurements –Nominal trajectory
composed of sub trajectories T1-T2 and T3.
Observation model of gyroscope: By integrating the
rotational velocity, the gyroscope model can be
expressed by the following equation:
(
)
(
) kk
l
θθ =
(6)
Each sensor described above is subject to
random noise. For instance, the encoders introduce
incremental errors (slippage), which particularly
affect the estimation of the orientation. For a
telemeter, let’s note various sources of errors:
geometric shape and surface roughness of the target,
beam width. For a gyroscope, the sources of errors
are: the bias drift, the nonlinearity in the scale factor
and the gyro’s susceptibility to changes in ambient
temperature. So, both the odometric and observation
models must integrate additional terms representing
these noises. Models inaccuracies induce also noises
which must be taken into account. It is well known
that the odometric model is subject to inaccuracies
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
448

caused by factors such as: measured wheel
diameters, unequal wheel-diameters, trajectory
approximation of robot between two consecutive
samples. These noises are usually assumed to be
Zero-mean white Gaussian with known covariance.
This hypothesis is discussed and reconsidered in the
proposed approach. Besides, an estimation error of
orientation introduces an ambiguity in the telemeters
measurements (one telemeter is assumed to measure
along X axis while it is measuring along Y axis and
vice-versa). This situation is particularly true when
the orientation is near angular bounds
l
θ and
m
θ .
This justifies the use of multiple model to reduce
measuring errors and efficiently manage robot’s
sensors. For this purpose, we have introduced the
concept of observation domain (boundary angles) as
defined in equations (4) and (5).
3 ROBUST MULTIPLE MODEL
FILTERING APPROACH
In this section, we present the data fusion and
filtering approach for the localization of a mobile
robot. In order to increase the robustness of the
localization and as discussed in section 2, the
localization process is decomposed into multiple
models. Each model is associated with a mode and
an interval of validity corresponding to the
observation domain; the aim is to consider only
reliable information by filtering erroneous
information. The localization is then considered as a
hybrid process. A Markov chain is employed for the
prediction of each model according to the robot
mode. The multiple model approach is best
understandable in terms of stochastic hybrid
systems. The state of a hybrid system consists of two
parts: a continuously varying base-state component
and a modal state component, also known as system
mode, that may only jump among points, rather than
vary continuously, in a (usually discrete) set. The
base state components are the usual state variables in
a conventional system. The system mode is a
mathematical description of a certain behavior
pattern or structure of the system. In our study, the
mode corresponds to the robot’s orientation. In fact,
the latter parameter governs the observation model
of telemeters along with observation domain. Other
parameters, like velocity or acceleration, could also
be taken into account for mode’s definition.
Updating of mode’s probability is carried out either
from a given criterion or from given laws
(probability or process). In this study, we assume
that each Markovian jump (mode) is observable
(Djama, 2001)(Dufour, 1994). The mode is
observable and measurable from the gyroscope.
3.1 Multiple Model Formulation
Let us consider a stochastic hybrid system. For a
linear process, the state and observation processes
are given by:
(
)
(
)( )
()( )()
kkk
kekke
kWkUkB
kkXAkkX
ααα
ααα
,,1,
,1/1,1/
+−⋅+
−−⋅=−
(7)
(
)
(
)
(
)( )
kkekke
kVkkXCkY αααα ,,1/, +−⋅=
(8)
For a nonlinear process, the state and observation
processes are described by:
(
)
(
)()
(
)
()
k
keke
kW
kUkkXFkkX
α
αα
,
1,,1/1,1/
+
−−−=−
(9)
(
)
(
)
(
)( )
kkeeke
kVkkXGkY
α
α
α
,,1/, +
−
=
(10)
where:
e
X is the base state vector;
e
Y is the noisy observation vector;
U is the input vector;
k
α is the modal state or system mode at
time k, which denotes the mode
during the k
th
sampling period;
W and V are the mode-dependent state and
measurement noise sequences,
respectively.
The system mode sequence
k
α is assumed for
simplicity to be a first-order homogeneous Markov
chain with the transition probabilities:
{
}
ij
i
k
j
k
P παα =
+
|
1
S
ji
∈∀ αα ,
where
j
k
α denotes that mode
j
α is in effect at time
k and S is the set of all possible system modes,
called mode space.
The state and measurement noises are of
Gaussian white type. In our approach, the state and
measurement processes are assumed to be governed
by the same Markov chain. However, it’s possible to
define differently a Markov chain for each process.
The Markov chain transition matrix is stationary and
well defined.
3.2 Variance Estimation Algorithm
It is well known that how poor estimates of noise
statistics may lead to the divergence of Kalman filter
and degrade its performance. To prevent this
divergence, we apply an adaptive algorithm for the
adjustment of the state and measurement noise
covariance matrices.
MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER FOR THE ROBUST LOCALIZATION OF A
MOBILE ROBOT
449

a. Estimation of measurement noise variance
Let ()
(
)
kR
i
2
,
ν
σ =
()
0
:1 ni = , be the measurement
noise variance at time
k for each component of the
observation vector.
0
n denotes the number of
observers (sensors number).
Let
() k β
ˆ
the squared mean error for stable
measurement noise variance:
() ()
∑
=
−=
n
j
i
k
n
k
0
2
1
1
ˆ
γβ
(11)
where
() k γ
represents the innovation.
For
1+n samples, the variance of () k β
ˆ
can be
written as:
()
()
()( )
()
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
⋅−−−⋅−
+
=
n
j
i
T
i
i
jkC
jkjkPjkC
n
kE
0
2
,
1,
1
1
ˆ
ν
σ
β
(12
)
Then, we obtain the estimation of the
measurement noise variance:
() ()
()()
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−⋅−−−
⋅−⋅
+
−−
=
∑
=
n
j
T
i
ii
i
jkCjkjkP
jkC
n
n
jk
n
0
2
2
,
0,
1,
1
1
max
ˆ
γ
σ
ν
(13)
The restriction with respect to zero is related to the
notion of variance.
A recursive formulation of the previous
estimation can be written:
() ( )
()
()()
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
Ψ⋅
+
−
+−−⋅+−= 0,
1
1
1
1
ˆ
max
ˆ
2
2
2
,
2
,
n
n
nk
k
n
kk
i
i
ii
γ
γ
σσ
νν
(14)
where:
() ( )
(
)()()
()()()()()
T
i
i
T
ii
nkCnknkP
nkCkCkkPkC
111,1
11,
+−⋅−+−+−
⋅+−−⋅−⋅=Ψ
(15)
b. Estimation of state noise variance
To estimate the state noise variance, we use the
same principle as in subsection a. One can write:
()
(
)
dine
QkkQ ⋅=
2
,
ˆ
ˆ
σ
(16)
By assuming that noises on the two encoder
wheels measurements obey to the same law and
have the same variance, the estimation of state noise
variance can be written:
()
()
(
)( )
() ()
() ()
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+⋅⋅+
+−+
⋅+⋅+−−
=
0
,
11
1
ˆ
1
,111
max
ˆ
2
,
2
2
,
T
idi
i
T
i
ii
in
kCQkC
kkC
kkPkCk
k
ν
σ
γ
σ
(17)
with:
() () ()
T
d
kBkBkQ ⋅=
ˆ
(18)
By replacing the measurement noise variance by
its estimate, we obtain a mean value given by the
following equation:
()
()
()
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−
⋅+
=
∑∑
==
0,
ˆ
1
1
max
ˆ
11
2
,
0
2
0
m
j
n
i
inn
jk
nm
k σσ
(19)
Where
m represents the sample number.
The algorithm described above carries out an on
line estimation of state and measurement noise
variances. Parameters
n and m are chosen
according to the number of samples used at time
k .
The noises variances are initialized from an “a
priori” information and then updated on line. In this
approach, variances are updated according the
robot’s mode and the measurement models.
For an efficient estimation of noise variances, an
ad hoc technique consisting in a measure selection is
employed. This technique consists of filtering
unreliable readings by excluding readings with weak
probability like the appearance of fast fluctuations.
For instance, in the case of Gaussian distribution, we
know that about 95% of the data are concentrated in
the interval of confidence
[
] σσ 2,2 +− mm where m
represents the mean value and
σ
the variance.
The sequence in which the filtering of the state
vector components is carried out is important. Once
the step of filtering completed, the probabilities of
each mode are updated from the observers (sensors).
One can note that the approach used here is close, on
one hand, to the Bayesian filter by the extrapolation
of the state probabilities, and on the other to the
filter with specific observation of the mode.
4 IMPLEMENTATION AND
SIMULATION RESULTS
The approach described above for robust
localization was applied for the mobile robot
described in section 2. The nominal trajectory of the
mobile robot includes three sub trajectories T1, T2
and T3, defining respectively a displacement along
X axis, a curve and a displacement along Y axis
(Fig. 2.). Note that the proposed approach remains
valid for any type of trajectory (any trajectory can be
approximated by a set of linear and circular sub
trajectories). In our study, we have considered three
models. This number can be modified according to
the environment’s structure, the type of trajectory
(robot rotating around itself, forward or backward
displacement, etc.) and to the number of observers
(sensors). Notice that the number of models
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
450

(observation and state) has no impact on the validity
of the proposed approach.
To demonstrate the validity of the proposed
approach (noticed AMM for Adaptive Multiple-
Model) and to show its effectiveness, we’ve
compared it to the following standard approaches:
Single-Model based EKF without estimation
variance (noticed SM), single-model based IEKF
(noticed SMI). For this purpose, simulations were
carried out to analyze the performances of each
approach in various scenarios.
For sub trajectories T1 and T3, filtering and data
fusion are carried out by iterative linear Kalman
filters due to linearity of the models, and for sub
trajectory T2, by iterative and extended Kalman
filters. The observation selection technique is
applied for each observer before the filtering step in
order to control, on one side, the estimation errors of
variances, and on the other, after each iteration, to
update the state noise variance. If an unreliable
reading is rejected at a given filtering iteration, this
has for origin either a bad estimation of the next
component of the state vector and of the prediction
of the corresponding observation, or a bad updating
of the corresponding state noise variance. The
iterative filtering is optimal when it is carried out for
each observer and no reading is rejected. In the
implementation of the proposed approach, the state
noise variance is updated, for a given mode
i , is
carried out according to the following filtering
sequence: x, y and then
θ
.
Notation
:
-
x
ε
, y
ε
and
εθ
: the estimation errors corresponding
to x, y and
θ
respectively;
-
Ndx , Ndy and
θ
Nd : the percentage of selected
data for filtering, corresponding to components
x
, y and
θ
respectively;
-
Ndxe , Ndye and eNd
θ
: the percentage of selected
data for estimation of the variances of state and
measurement noises, corresponding to components
x
,
y
and
θ
respectively.
-+:SMI; °: SMI, --:AMM
Scenario 1
-Noise-to-signal Ratio of odometric sensors: right
encoder: 8%, left encoder: 8%
-Noise-to-signal Ratio of Gyroscope: 3%
-Noise-to-signal Ratio of telemeter 1: 10% of the
odometric elementary step
-Noise-to-signal Ratio of telemeter 2: 10% the
odometric elementary step
-“A priori” knowledge on the variance in initial
state: Good
-“A priori” knowledge on noise statistics
(measurement and state variances): Good
In this scenario, the telemeters measurement noise is
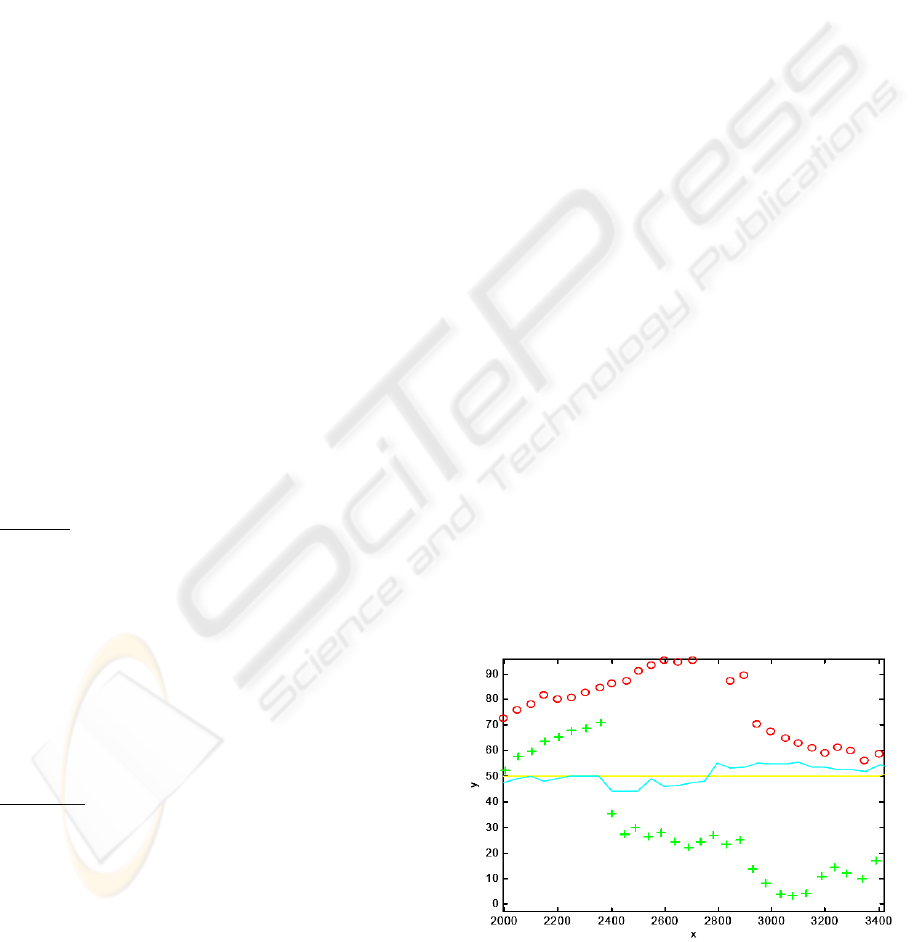
higher than state noise. We notice that performances
of AMM filter are better that those of SM and SMI
filters concerning x and y-components (Table 1; Fig.
3-5). In sub trajectory T3, the orientation’s
estimation error relating to AMM filter (Table 1) has
no influence on filtering quality of the remaining
components of state vector. Besides, one can note
that this error decreases in this sub trajectory (Figure
6). In this case, only gyroscope is used for the
prediction and updating the Markov chain
probabilities. In sub trajectory T2, we notice that the
estimation error along x-Axis for AMM filter is
lightly higher than those relating to other filters. This
error is concentrated on first half of T2 sub
trajectory (Figure 7) and decreases then on second
half of the trajectory. This can be explained by the
fact that on one hand, the estimation variances
algorithm rejected 0.7% of data, and on the other,
the filtering step has rejected the same percentage of
data. This justifies that neither the variances
updating, nor the x-coordinate correction, were
carried out.
Note that unlike filters SM and SMI, filter AMM
has a robust behavior concerning pose estimation
even when the signal-to-noise ratio is weak. By
introducing the concept of observation domain for
observation models, we obtain a better modeling of
observation and a better management of robot’s
sensors. The last remark is related to the bad
performances of filters SM and SMI when the
signal-to-noise ratio is weak. This ratio degrades the
estimation of the orientation angle, observation
matrices, Kalman filter gain along with the
prediction of the observations.
Figure 3: Estimated trajectories (sub trajectory T1).
MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER FOR THE ROBUST LOCALIZATION OF A
MOBILE ROBOT
451

4000 4100 4200 4300 4400 4500 4600 4700 4800
200
300
400
500
600
700
800
900
1000
1100
1200
x
y
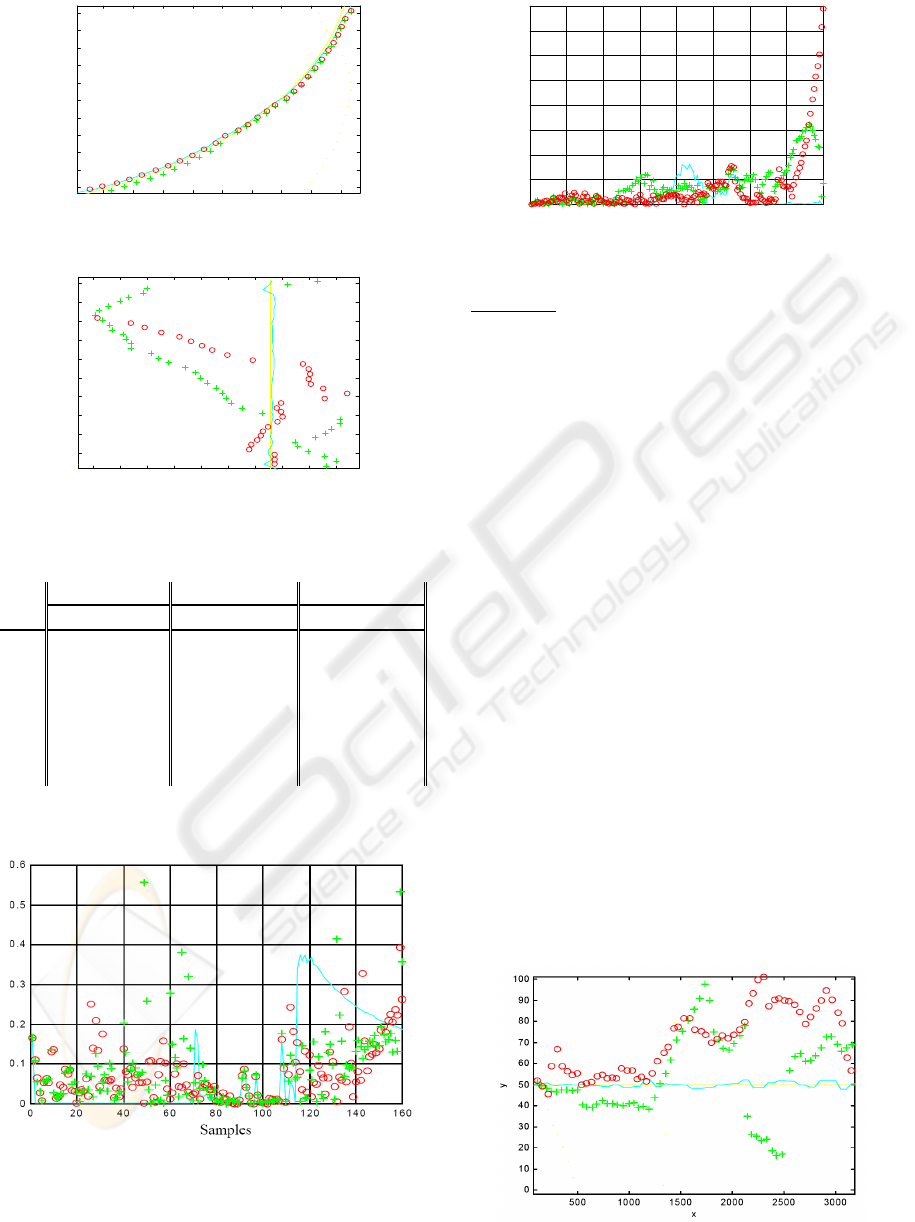
Figure 4: Estimated trajectories (sub trajectory T2).
4770 4780 4790 4800 4810 4820 4830 4840 4850 4860
2000
2200
2400
2600
2800
3000
3200
3400
3600
3800
x
y
Figure 5: Estimated trajectories (sub trajectory T3).
Table 1: Average estimation errors (Scenario 1).
T1 T2 T3
SM SMI AMM SM SMI AMM SM SMI AMM
x
ε
(
cm)
6.2
5
3.2
3
2.5
13.
2
10.8
15.
3
31.
9
31.
2
1.2
y
ε
(
cm)
13.
6
16.
7
2.3
23.
9
11.9
8.2
5
19.
2
5.7
5
3.2
3
εθ
(10
-3
rad)
81.
1
66.
9
3.8
32.
2
39.9
35.
6
136 125
267
.9
Ndx =99.37%, Ndy = 84.37%,
θ
Nd =99.37%,
Ndxe =99.37%, Ndye =97.5%, eNd
θ
=99.37%.
AAAAAAA
Figure 6: Orientation error.
0 20 40 60 80 100 120 140 160
0
20
40
60
80
100
120
140
160
N b h till
Samples
Figure 7: Position error with respect to X axis.
Scenario 2
-Noise-to-signal Ratio of odometric sensors: right
encoder: 10%, left encoder: 10%
-Noise-to-signal Ratio of Gyroscope: 3%
-Noise-to-signal Ratio of telemeters: 4% of the
odometric elementary step (40% of the state noise)
-“A priori” knowledge on the variance in initial
state: Good
-“A priori” knowledge on noise variances (i)
telemeters and state: Good; (ii) gyroscope: Bad
The results presented here (Table 2 and Fig. 8-
10) show the influence of signal-to-noise ratio and
the estimation of noise variances on performances of
SM and SMI filters. In this scenario, the initial
variance of measurement noise of the gyroscope is
incorrectly estimated. Contrary to AMM approach,
filters SM and SMI do not carry out any adaptation
of this variance, leading to unsatisfactory
performance.
Figure 11 illustrates the evolution of state noise
variance estimate compared to the average variance.
Note that the ratio between variances reaches 1.7 on
sub trajectory T1, 3.0 on sub trajectory T2, and 3.3
on sub trajectory T3. It is important to mention that
the algorithm proposed for estimation of variances
estimates the actual value of state noise variance and
not its average value. These results are related to the
fact that the signal-to-noise ratio is weak both for the
odometer and the telemeters.
Figure 8: Estimated trajectories (sub trajectory T1).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
452

3600 3800 4000 4200 4400 4600 4800
200
400
600
800
1000
1200
x
y
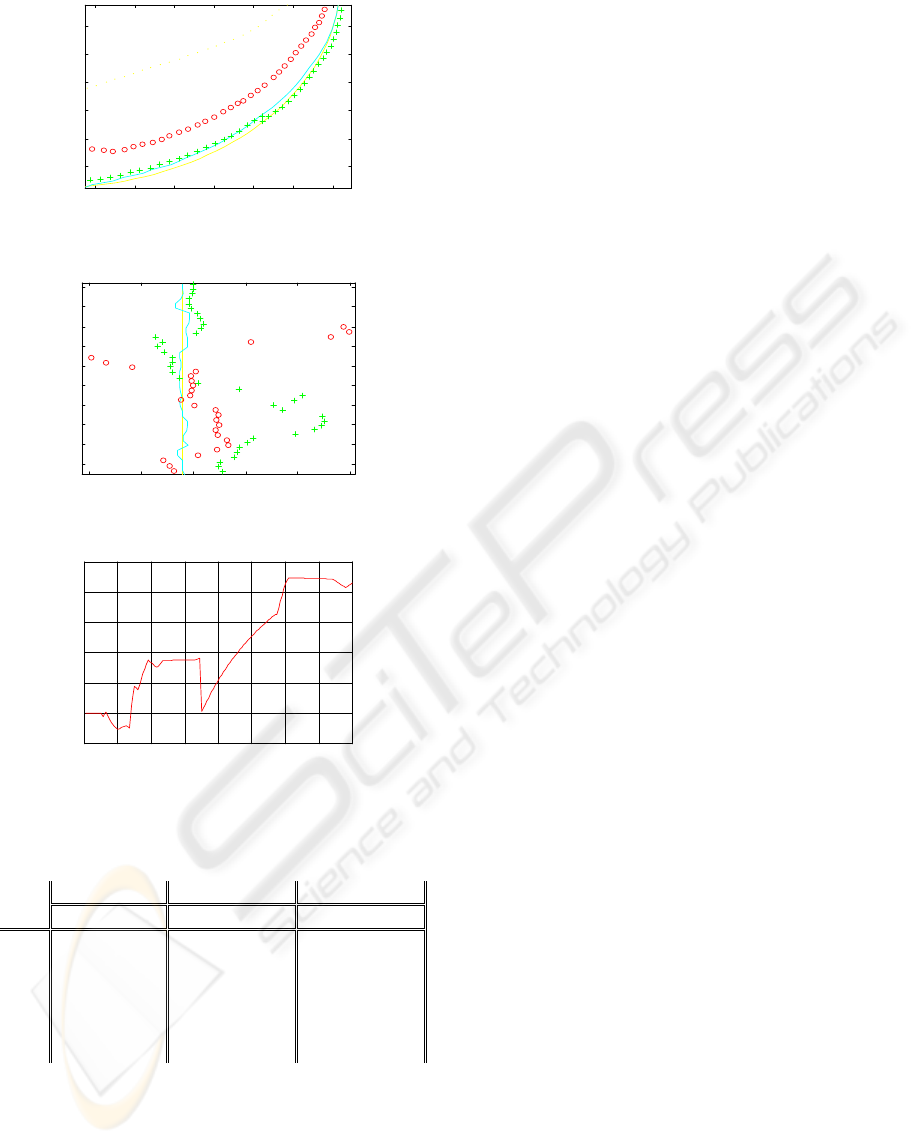
Figure 9: Estimated trajectories (sub trajectory T2).
4800 4820 4840 4860 4880 4900
2000
2200
2400
2600
2800
3000
3200
3400
3600
3800
x
y
Figure 10: Estimated trajectories (sub trajectory T3).
0 20 40 60 80 100 120 140 160
0.5
1
1.5
2
2.5
3
3.5
béh ill
Samples
Figure 11: Ratio between the estimate of state noise
variance and the average variance.
Table 2: Average estimation errors (Scenario 2).
T1 T2 T3
SM SMI AMM SM SMI AMM SM SMI AMM
x
ε
(cm
)
11.
7
11 1.8 19 75 13.6 17.3 40 1.3
y
ε
(cm
)
16.
7
21 1 39
17
9
17.4 15.7
11
7
1.93
εθ
(10
-3
rad)
99.
3
12
9
1.5 42.9
17
5
35.4 97.5
16
7
37.8
Ndx =87.5%, Ndy =66%,
θ
Nd =99.37%, Ndxe =87.5%,
Ndye =82.5%, eNd
θ
=99.37%.
5 CONCLUSIONS
We presented in this paper a multiple model
approach for the robust localization of a mobile
robot. In this approach, the localization is considered
as a hybrid process, which is decomposed into
multiple models. Each model is associated with a
mode and an interval of validity corresponding to
the observation domain. A Markov chain is
employed for the prediction of each model according
to the robot mode. To prevent divergence of
standard Kalman Filtering, we proposed the
application of an adaptive algorithm for the
adjustment of the state and measurement noise
covariance matrices. For an efficient estimation of
noise variances, we used an ad hoc technique
consisting of a measure selection for filtering
unreliable readings. The simulation results which we
obtain in different scenarios show better
performances of the proposed approach compared to
standard existing filters. These investigations into
utilizing multiple model technique for robust
localization show promise and demand continuing
research.
REFERENCES
J. Borenstein, B. Everett, L. Feng, Navigating Mobile
Robots: Systems and Techniques. A.K. Peters, Ltd.,
Wellesley, MA, 1996.
C. Harris, A. Bailley, T. Dodd, Multi-sensor data fusion in
defense and aerospace, Journal of Royal Aerospace
Society, 162 (1015) (1998) 229-244.
J.B. Gao, C.J. Harris, Some remarks on Kalman filters for
the multi-sensor fusion, Journal of Information
Fusion, 3 (2002) 191-201.
C. Chui, G. Chen, Kalman filtering with real time
applications, Springer Series in Information Sciences,
Springer-Verlag, New-York 17 (1987) 23-24.
K.O. Arras, N. Tomatis, B.T. Jensen, R. Siegwart,
Multisensor on-the-fly localization: precision and
reliability for applications, Robotics and Autonomous
Systems, 34 (2001) 131–143.
S. Borthwick, M. Stevens, H. Durrant-Whyte, Position
estimation and tracking using optical range data,
Proceedings of the IEEE/RSJ International
Conference on Intelligent Robots and Systems, 1993,
pp. 2172–2177.
P. Jensfelt, H.I. Christensen, Pose tracking using laser
scanning and minimalistic environment models, IEEE
Transactions on Robotics and Automation, 17 (2)
(2001) 138–147.
J. Neira, J.D. Tardós, J. Horn, G. Schmidt, Fusing range
and intensity images for mobile robot localization,
IEEE Transactions on Robotics and Automation, 15
(1) (1999) 76–84.
MULTIPLE MODEL ADAPTIVE EXTENDED KALMAN FILTER FOR THE ROBUST LOCALIZATION OF A
MOBILE ROBOT
453

J.A. Pérez, J.A. Castellanos, J.M.M. Montiel, J. Neira, J.D.
Tardós, Continuous mobile robot localization: vision
vs. laser, Proceedings of the IEEE International
Conference on Robotics and Automation, 1999, pp.
2917–2923.
G.A. Borges, M.J. Aldon, Robustified estimation
algorithms for mobile robot localization based
geometrical environment maps, Robotics and
Autonomous Systems, 45 (2003) 131-159.
L. Kleeman, Optimal estimation of position and heading
for mobile robots using ultrasonic beacons and dead-
reckoning, Proceedings of the IEEE International
Conference on Robotics and Automation, 1992, pp.
2582–2587.
L. Jetto, S. Longhi, G. Venturini, Development and
experimental validation of an adaptive Kalman filter
for the localization of mobile robots, IEEE
Transactions on Robotics and Automation, 15 (2)
(1999) 219–229.
S.J. Julier, J.K. Uhlmann, A non-divergent estimation
algorithm in the presence of unknown correlations,
Proceedings of the American Control Conference,
1997.
X. Xu, S. Negahdaripour, Application of extended
covariance intersection principle for mosaic-based
optical positioning and navigation of underwater
vehicles, Proceedings of the IEEE International
Conference on Robotics and Automation, 2001, pp.
2759–2766.
Z. Djama, Y. Amirat, Multi-model approach for the
localisation of mobile robots by multisensor fusion,
Proceedings of the 32th International Symposium On
Automotive Technology and Automation, 14th-18th
june 1999, Vienna, Autriche, pp. 247-260.
Z. Djama, Approche multi modèle à sauts Markoviens et
fusion multi capteurs pour la localisation d’un robot
mobile. PhD Thesis, University of Paris XII, May
2001.
H. A. P. Blom and Y. Bar-Shalom, The interacting
multiple model algorithm for systems with Markovian
switching coefficients, IEEE Trans. Automat. Contr.,
vol. 33, pp. 780–783, Aug. 1988.
X. R. Li, Engineer’s guide to variable-structure multiple-
model estimation for tracking, in Multitarget-
Multisensor Tracking: Applications and Advances, Y.
Bar-Shalom and D.W. Blair, Eds. Boston, MA: Artech
House, 2000, vol. III, ch. 10, pp. 499–567.
X. R. Li, Hybrid estimation techniques, Control and
Dynamic Systems: Advances in Theory and
Applications, C. T. Leondes, Ed. New York:
Academic, 1996, vol. 76, pp. 213–287.
E. Mazor, A. Averbuch, Y. Bar-Shalom, and J. Dayan,
Interacting multiple model methods in target tracking:
A survey, IEEE Trans. Aerosp. Electron. Syst., vol.
34, no. 1, pp. 103–123, 1996.
F. Dufour, Contribution à l’étude des systèmes linéaire à
saut markoviens, PhD Thesis, University of Paris Sud
University, France, 1994.
M. Oussalah, Suboptimal Multiple Model Filter for
Mobile Robot Localization, International Journal of
Robotics Research, vol. 20, no. 12, December 2001,
pp. 977-989.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
454