OPTIMIZATION MODEL AND DSS

FOR MAXIMUM RESOLUTION DICHOTOMIES

James K. Ho

Department of Information and Decision Sciences, University of Illinois at Chicago, IL 60607, USA

Sydney C. K. Chu

Department of Mathematics, University of Hong Kong, Pokfulam Road, Hong Kong SAR, China

S. S. Lam

School of Business and Administration, The Open University of Hong Kong, Hong Kong SAR, China

Keywords: Data mining, decision support system, maximum resolution topology, multi-attribute dichotomy, goal

programming, optimization modelling.

Abstract: A topological model is presented for complex data sets in which the attributes can be cast into a dichotomy.

It is shown that the relative dominance of the two parts in such a dichotomy can be measured by the

corresponding areas in its star plot. An optimization model is proposed to maximize the resolution of such a

measure by choice of configuration of the attributes, as well as the angles among them. The approach is

illustrated with the case of online auction markets, where there is a buyer-seller dichotomy as to whether

conditions are favourable to buyers or sellers. An implementation of the methodology in a spreadsheet

based DSS is demonstrated. Its ease of use is promising for diverse applications.

1 INTRODUCTION

A topological model for a high dimensional data set

is a simultaneous graphical display of all its relevant

attributes, which provides a geometrical shape as a

descriptive, visual statistics of the underlying

construct engendering the data. In particular, when

various dimensions can be identified to form a

multi-attribute dichotomy, the area spanned by the

two halves of the topological model can be used as a

measure of the relative dominance of the two parts

of the dichotomy. Using a reference subset of

prejudged cases, the configuration of the dimensions

and the angles among them can be optimized in a

Goal Programming (Scniederjans, 1995) model for a

topology that maximizes the resolution of such

dichotomies. Applications abound in diverse fields,

including diffusion of innovation (Ho, 2005),

investment climate and business environment (Ho,

2006a), marketing research and customer relations

management (Ho, 2006b), and medical diagnostics.

The implementation of the optimization model as an

easy-to-use, spreadsheet based DSS is described. It

is illustrated by the case of topological analysis of

online auction markets (Ho, 2004) where it is of

interest to discern whether particular markets are

favourable to buyers or sellers.

2 TOPOLOGICAL ANALYSIS

Visualization has been a fast developing approach in

data-mining (Hoffman and Grinstein, 2001) in which

graphical models are constructed to provide visual

cues for pattern recognition and knowledge

discovery from complex data. In the study of

financial markets (stock and commodity), the

dimension of interest is primarily prices, or the

fluctuation thereof. Complexity arises from the large

number of instruments involved. The best known

examples of visualization models for stock markets

are based on the tree-map method (Shneiderman,

355

K. Ho J., C. K. Chu S. and S. Lam S. (2007).

OPTIMIZATION MODEL AND DSS FOR MAXIMUM RESOLUTION DICHOTOMIES.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 355-358

DOI: 10.5220/0001630803550358

 SciTePress

1992), and the minimum-spanning-tree method

(Vandewalle et al, 2001). For auction markets, the

game-theoretic dynamics itself gives rise to higher

dimensional complexity. And with online auctions

removing conventional constraints on time and

space, their activities and impact on e-commerce can

only be expected to grow exponentially. In this

regard, the availability of operational data from

eBay.com presents unprecedented challenges and

opportunities for insight into online auction markets.

In (Ho, 2004), twelve dimensions (i.e. attributes) are

identified as follows.

1. NET ACTIVITY (auctions with bids)

2. PARTICIPATION (average number of bids per

auction)

3. SELLER DIVERSITY (distribution of offers)

4. SELLER EXPERIENCE (distribution of sellers'

ratings)

5. MATCHING (auctions ending with a single bid)

6. SNIPING (last minute winning bids)

7. RETAILING (auctions ending with the Buy-It-

Now option)

8. BUYER DIVERSITY (distribution of bidder

participation)

9. BUYER EXPERIENCE (distribution of buyers'

ratings)

10. DUELING (evidence of competitive bidding)

11. STASHING (evidence of stock-piling)

12. PROXY (use of proxy bidding as evidence of true

valuation)

Our topological model is based on the star plot for

displaying multivariate data with an arbitrary

number of dimensions (Chambers et al, 1983). Each

data point is represented as a star-shaped figure (or

glyph) with one ray for each dimension. As the

resulting shapes depend on the configuration of the

dimensions, we further analyse the observations

along the dimensions identified above in an effort to

present a visual model of the shape of online auction

markets.

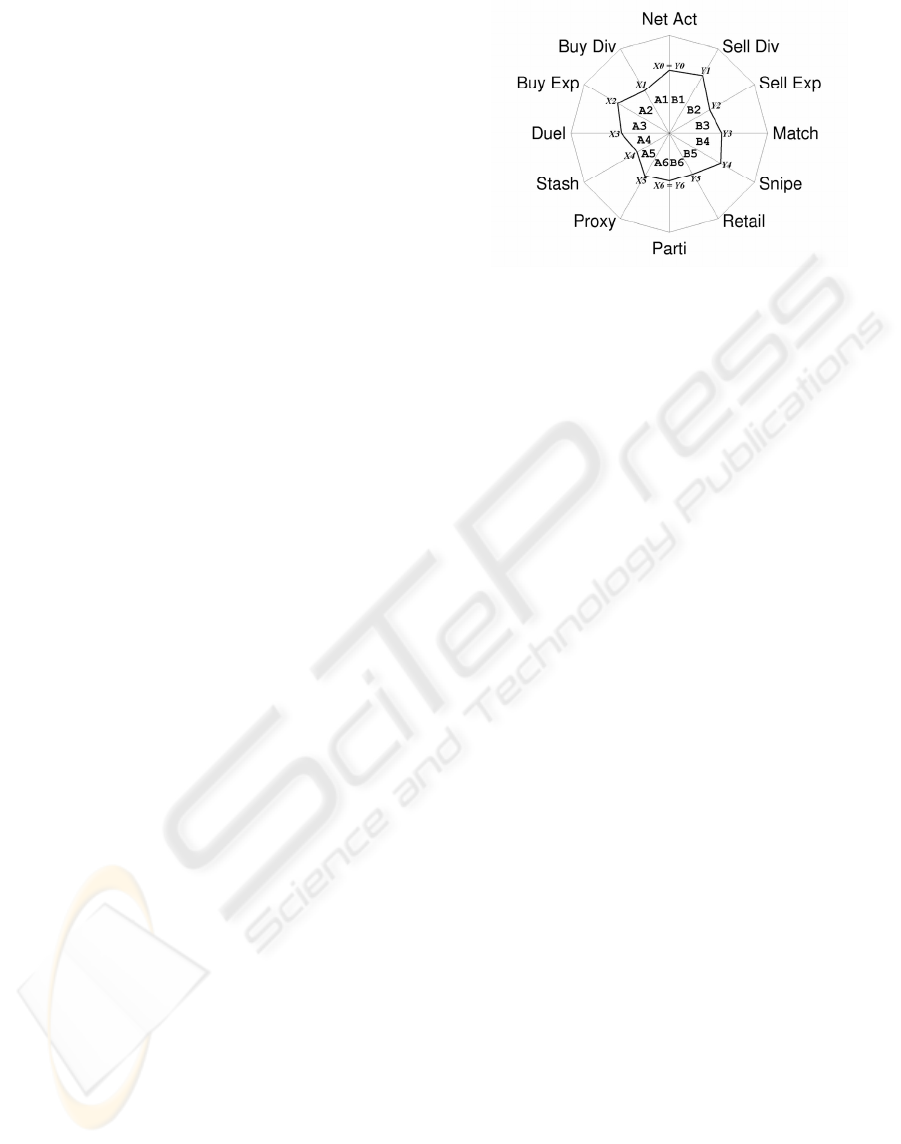
To discern whether particular market conditions

are favourable to buyers or sellers, we divide the

dimensions into a buyer-seller dichotomy as shown

in Figure 1 where buyer dimensions (

SELLER

DIVERSITY, SELLER EXPERIENCE, MATCHING,

SNIPING, RETAILING)

are grouped to the right, and

seller dimensions (

BUYER DIVERSITY, BUYER

EXPERIENCE, DUELING, STASHING, PROXY) are

grouped to the left. The other dimensions (NET

ACTIVITY, PARTICIPATION)

are neutral and

mapped to the vertical axis.

Figure 1: Topological model of online auction market.

3 MAXIMUM RESOLUTION

TOPOLOGY

In general, a multi-attribute dichotomy is any multi-

dimensional dataset in which the dimensions can be

partitioned into two groups, each contributing to one

part of the dichotomy. Given the star glyph of a

multi-attribute dichotomy, as exemplified in Figure

1, it will be both visually and intuitively appealing if

the areas covered by the two parts can be used as a

meaningful aggregate measure of their relative

dominance. A larger area on the left side of the

glyph means dominance by the left part, and vice

versa. In the case of online auction markets, this

asymmetry can be interpreted as market conditions

being advantageous to either buyers or sellers. In

mathematical terms, the aggregate value function

takes the form of the sum of pair-wise products of

adjacent attributes: V(X

, …, X

) = C Σ X

;

where attributes i and j are adjacent; X

is the value

of attribute i, for i = 1, …, n; and C is some scaling

constant.

The concept of using the area of the parts of a

dichotomy as an aggregate measure of their relative

dominance is plausible, since increasing value of an

attribute contributes positively to its designated part,

as well as the latter’s area in the glyph. However, it

must be refined to realize its potential, which arises

from the degrees of freedom allowed by the

topology of the glyph, namely, the configuration of

the attributes, and the angles between adjacent pairs

thereof. For any given arrangement of the attributes,

the standard star plot produces a glyph along

symmetrically spaced radial axes. Variations from

this symmetry imply a feasible set of shapes and

areas, which along with permutations of the

configuration, offer the choice of topologies that

may suit further criteria for a meaningful aggregate

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

356

measure function. In particular, we use a diverse

subset of the data instances in an optimization model

to derive a topology with maximum resolution in

discerning dominance with respect to the reference

subset (Ho and Chu, 2005).

To this end, the first step is to render the glyph

unit free by normalizing the data on each dimension

to the unit interval [0, 1]. The second step is to

render the glyph context free by harmonizing the

dimensions as follows. For each attribute, the

quartiles for the values in the entire dataset are

computed. A spline function (Cline, 1974) is

constructed to map these quartiles into the [0.25, 0.5,

0.75] points of the unit interval. This way, a

hypothetical data instance with all attributes at mean

values of the dataset will assume the shape of a

symmetrical polygon with vertices at the mid-point

of each radial axis. In this frame of reference, all

shapes and sizes are relative to this generic

“average” glyph, and free of either units or specific

context of the attributes. For our exploratory work,

simple second-order (piecewise linear) splines are

used.

3.1 Dichotic Dominance with respect to

Reference Subsets

Next, to determine an optimal topology, we use the

concept of a reference subset of the data instances to

help define dichotic dominance. This concept is best

explained in a medical scenario. Suppose a certain

disease is monitored by a number of symptoms and

tests, with a dichotic prognosis of “life” or “death”.

Judging from the combination of data for any

particular case, it may be difficult to predict. A

reference subset is a collection of non-trivial, non-

obvious cases with known outcomes, namely life or

death. In our exploratory analysis of online auction

markets, there is no factual or expert judgment on

whether any particular case is a “buyers” or “sellers”

market. An initial collection from 34 diverse and

well-established markets is used on an ad hoc basis

as the reference subset. An arbitrary configuration of

the attributes within each part of the dichotomy is

selected with the attributes evenly spaced, as in

Figure 1. This is analogous to selecting a portfolio of

stocks to provide an index for a stock market. The

performance of any stock can be gauged relative to

the index, which may be arbitrarily chosen initially.

With better knowledge of the significance of

individual stocks, more useful indices can be

established. By the same token, the choice of

reference subsets for multi-attribute dichotomies can

be adaptively refined as the study progresses.

Once an optimal topology is derived with respect

to a given reference subset, any other data instance,

an online auction market in our case, can be plotted

and visualised as a maximum resolution dichotomy.

Moreover, the total enclosed area in the plot,

including both parts of the dichotomy may be used

as a relative measure of the overall activity of all the

attributes. We can consider this as an indicator of the

“robustness” of the market. Whereas, the difference

in the areas of the left and right parts of the

dichotomy provides an index of dichotic dominance

among market conditions favouring buyers and

sellers. In our settings, a left dominance favours

sellers, and a right dominance favours buyers.

3.2 A Goal Programming Optimization

Model

Subject to the constraints of preserving the

prejudged dominance in the reference subset of

dichotomies, an optimal topology (configuration of

attributes and angles between adjacent pairs) is

sought that maximises the discriminating power, or

resolution, as measured by the sum of absolute

differences in left and right areas for the reference

subset. Such an optimal configuration will be called

a maximum resolution topology (MRT). For any

given configuration of the attributes, maximization

of the discriminating power can be formulated as a

linear program (LP). However, LP produces

extreme-point solutions, which may reduce some of

the angles between attributes to zero, thus collapsing

the glyph. To avoid such degeneration,

maximization with bounded variation of the angles

is modelled as a goal program (GP) in (Ho and Chu,

2005).

4 DSS FOR MRT

To facilitate the computation of a maximum

resolution topology (MRT) for a given set of data

from a multi-attribute dichotomy, an easy-to-use

decision support system (DSS) has been built on

Excel spreadsheet software. Such an MRT-DSS

system has both its front end and report routine

integrated in the same Excel spreadsheet workfile,

into which the input data records can be placed (for

example, imported from a database); and outputs of

values and MRT-star plots displayed.

To find the solution, the user only needs to copy

and paste the records of training data (the “reference

OPTIMIZATION MODEL AND DSS FOR MAXIMUM RESOLUTION DICHOTOMIES

357

set”) to the ‘Training Data’ worksheet and click the

‘Solve!’ item button on the ‘MRT’ menu. MRT-DSS

will permute over all possible configurations and

dynamically generate the input data for each

configuration. The training data will be passed to a

linear programming solver (LINGO Version 8) to

find the solution based on the MRT-GP model.

MRT-DSS will store the solution of each

configuration on the ‘Work’ worksheet, as well as

the best solution on the ‘Best solution’ worksheet. It

will also keep the optimal MRT configuration and

angles in the ‘StarPlot’ worksheet for preparing the

test data for plotting.

By completing the training of MRT-DSS and

obtaining the optimal configuration, the system can

then be used to evaluate new cases of the dichotic

model. With data copied to the ‘Testing Data’

worksheet, the ‘Prepare StarPlot Data’ item on the

‘MRT’ menu is selected. MRT-DSS will transpose

and store the data in the ‘StarPlot’ worksheet. It will

also compute for each test case the areas of the left

(A) and right (B) parts of the dichotomy and their

difference (A-B). The user can easily evaluate the

test cases based on these numerical results. To

visualize and further analyze a particular data

record, the user can choose the ‘Plot Solution’ item

on the ‘MRT’ menu to draw its StarPlot diagram

under the maximum resolution topology. By

inspecting and comparing records under the optimal

configuration and angles in the diagrams, and by

studying the left-right differentials provided by

MRT-DSS, substantial topological analysis can be

performed for insight into the model under study.

5 CONCLUSIONS

We presented an optimization model to derive a

maximum resolution topology for complex data sets

that can be cast as multi-attribute dichotomies.

While we used only the buyer-seller dichotomy for

online auction markets as illustration, applications

have already resulted in diverse fields (Ho, 2005,

2006a, b). For future work, we expect ample

innovative applications of the methodology with the

help of the easy-to-use DSS.

ACKNOWLEDGEMENTS

This work is partially supported by the Hong Kong

RGC Competitive Earmarked Research Grant

(CERG) Award: HKU 7126/05E.

REFERENCES

Chambers, J., Cleveland, W., Kleiner, B. and Tukey, P.,

1983. Graphical Methods for Data Analysis, Belmont,

CA: Wadsworth Press.

Cline, A. K., 1974. ‘Scalar- and planer-valued curve

fitting using splines under tension’, Communications

of the Association for Computing Machinery 17: pp.

218–220.

Ho, J. K.,2004. ‘Topological analysis of online auction

markets’, International Journal of Electronic Markets

14(3): pp. 202–213.

Ho, J. K., 2005. ‘Maximum resolution dichotomy for

global diffusion of the Internet’, Communications of

the Association for Information Systems 16:pp.797–

809.

Ho, J. K., 2006a. ‘Maximum resolution dichotomy for

investment climate indicators’, International Journal

of Business Environment 1(1): pp.126–135.

Ho, J. K., 2006b. ‘Maximum resolution dichotomy for

customer relations management’, in Zanansi, A. et al

(eds.) Data Mining VII, WIT Press, Southampton, pp.

279–288.

Ho, J. K. and Chu, S. C. K. (2005) ‘Maximum resolution

topology for multi-attribute dichotomies’, Informatica

16 (4): pp. 557–570.

Ho, J. K. and Chu, S. C. K. and Lam, S.S. (2007)

‘Maximum resolution topology for online auction

markets’, International Journal of Electronic Markets

17(2) (to appear).

Hoffman, Patrick and Grinstein, George, 2001. ‘A survey

of visualizations for high-dimensional data mining’, in

Usama Fayyad et al (eds.) Information Visualization in

Data Mining and Knowledge Discovery, Morgan

Kaufmann: pp. 47–82.

Roth, Alvin E. and Ockenfels, Axel (2002) ‘Last minute

bidding and the rules for ending second-price auctions:

theory and evidence from A natural experiment on the

Internet’, American Economic Review 92(4): pp.

1093–1103.

Scniederjans, M. J., 1995. Goal Programming

Methodology and Applications, Kluwer publishers,

Boston.

Shneiderman, B., 1992. Tree visualization with tree-maps:

a 2-D space-filling approach. ACM Transactions on

Graphics 11: pp. 92–99

Tukey, J.W., 1997. Exploratory Data Analysis. Addison-

Wesley, Reading, MA.

Vandewalle, N., Brisbois, F., Tordoir, X., 2001. ‘Non-

random topology of stock markets’. Quantitative

Finance 1: pp. 372–374.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

358