TRACKING PLASMA ETCH PROCESS VARIATIONS USING

PRINCIPAL COMPONENT ANALYSIS OF OES DATA

Beibei Ma, Seán McLoone and John Ringwood

Department of Electronic Engineering, National University of Ireland Maynooth, Maynooth, Ireland

Keywords: Semiconductor manufacturing, plasma etching, metal etching, optical emission spectroscopy (OES),

principal component analysis (PCA), batch processing.

Abstract: This paper explores the application of principal component analysis (PCA) to the monitoring of within-lot

and between-lot plasma variations that occur in a plasma etching chamber used in semiconductor

manufacturing, as observed through Optical Emission Spectroscopy (OES) analysis of the chamber exhaust.

Using PCA, patterns that are difficult to identify in the 2048-dimension OES data are condensed into a

small number of principle components (PCs). It is shown, with the aid of experimental data, that by simply

tracking changes in the directions of these PCs both inter-lot and intra-lot patterns can be identified.

1 INTRODUCTION

Modern day semiconductor manufacturing is a

highly competitive business in which companies are

required to produce vast quantities of reliable high

performance integrated circuits (ICs) at low cost. As

such, close monitoring and tight control of hundreds

of complex process steps are needed to maintain

production standards and high product throughput.

In this context we focus on plasma etching of

semiconductor wafers, an important process step in

the manufacture of many ICs (Sugawara, 1998). A

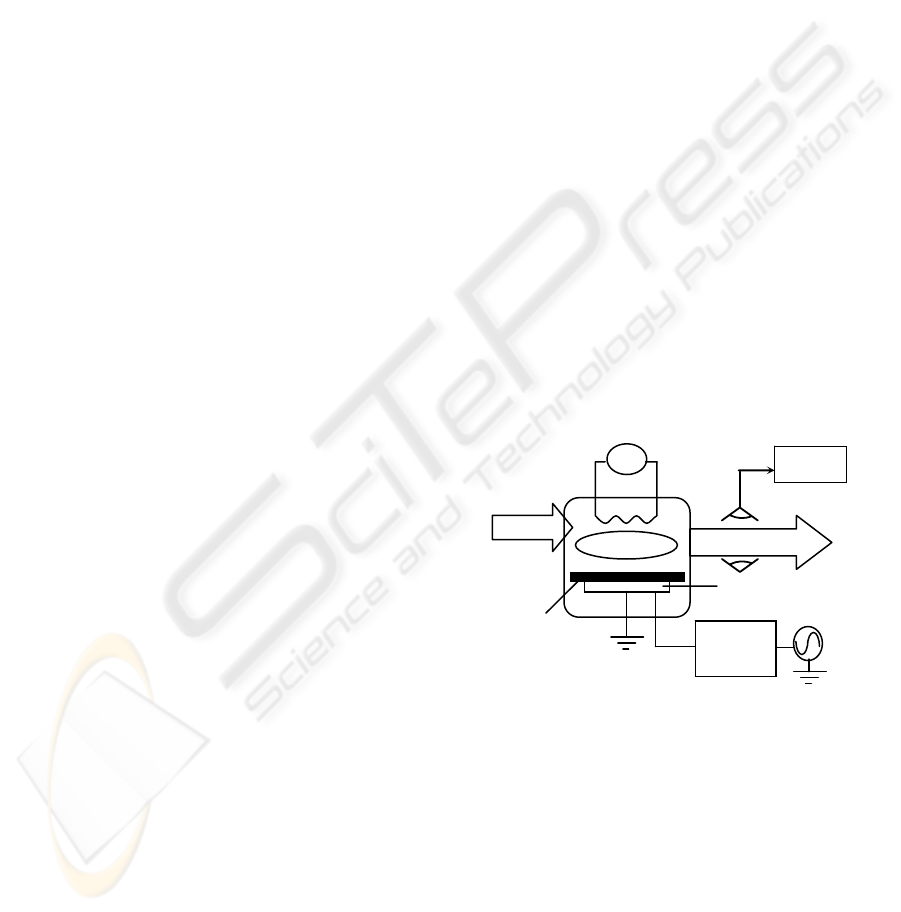
typical reaction ion etching (RIE) chamber is

illustrated in Fig. 1. Gas is pumped into the chamber

under vacuum and ionised using a high power

Microwave (MF) source to create a plasma. A radio

frequency (RF) electromagnetic field accelerates the

resulting ionised species towards the electrode,

where they interact both chemically and physically

with the wafer, etching away the exposed surface.

The etch rate and profile obtained are determined in

a complex and nonlinear fashion by the plasma

chemistry and energy as well as several process

variables including gas flow rates and RF power.

Monitoring the chemistry of the plasma in the

chamber can be achieved using Optical Emission

Spectroscopy (OES) (Splichal et al., 1987). In the

plasma chamber considered in this study the OES

data is collected for the exhaust plasma leaving the

chamber using a 2048 wavelength OES sensor

(170nm to 875nm) with a sampling interval of 0.75s.

Using this setup OES data was collected for 17 lots

of 24 wafers, with each waver undergoing a two step

etch process lasting 45s. A sample OES data set for

a single wafer is shown in Fig. 2.

Exhaust

Plasma

BCl

, Cl

Wafer

Electrode

Match

box

OES

Figure 1: Diagram of a plasma etching chamber.

With the OES footprint of each wafer having

dimensions of 60

2048, direct visualisation and

monitoring of variations in the plasma chemistry

across wafers and across lots is impractical.

Fortunately, optical emission spectra are inherently

highly redundant making it possible to achieve

substantial data compression using Principle

Component Analysis (PCA) techniques without

loosing valuable information on plasma changes. In

this paper we show that simply monitoring changes

361

Ma B., McLoone S. and Ringwood J. (2007).

TRACKING PLASMA ETCH PROCESS VARIATIONS USING PRINCIPAL COMPONENT ANALYSIS OF OES DATA.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 361-364

DOI: 10.5220/0001629303610364

 SciTePress

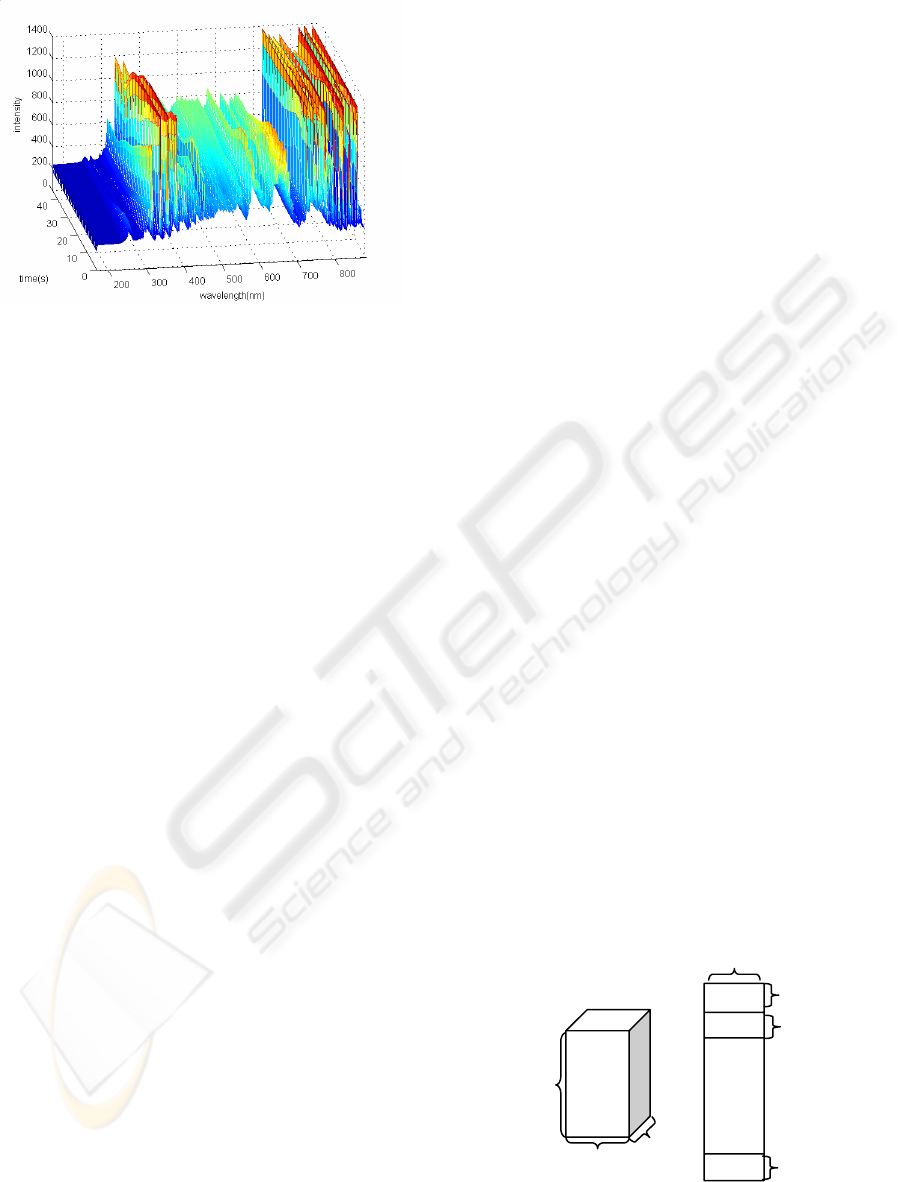
Figure 2: A plasma etch OES data set for a single wafer.

in the directions of the principle component loading

vectors, computed on either a wafer-by-wafer or lot-

by-lot basis, is sufficient to detect valuable

information on process trends that are not

immediately apparent when looking at the OES data

as a whole.

2 PRINCIPAL COMPONENT

ANALYSIS

Principal component analysis (PCA) is a linear

multivariate data projection technique widely used

for data compression and analysis (Jackson, 1991). It

provides a means of generating low dimension

representations of high dimension datasets while

retaining the maximum amount of information.

2.1 Definition

PCA is a method of writing a matrix X of rank r as

a sum of r matrices of rank 1,

where the rank 1

matrices are expressed as outer products of two

vectors, a score

t and a loading

p (Jackson, 1991)

∑

ptX

(1)

The loading vectors,

p , are eigenvectors of the

matrix

, that is

iii

ppXX

=)(

(2)

where

λ is the eigenvalue associated with the i

eigenvector

p . The loading vectors

p describe the

principal directions of variation in X, are orthogonal

to each other:

≠∀= ,pp 0

(3)

and have unit length, while the eigenvalues indicate

the amount of variance represented by each

direction. For a given

X and

p , the corresponding

score vector

t is given by:

Xpt

(4)

A principle component (PC) model of

is then

obtained by selecting the components

),(

tp with

the largest eigenvalues to represent it. When data

redundancy is high two or three PCs are often

sufficient to obtain a good model.

Essentially, PCA projects a high dimensional

data space onto a lower dimensional sub-space

where the axes are the PC loading vectors and the

coordinates of the data the PC score vectors.

Singular Value Decomposition (SVD) can be

used to calculate all r principal components in one

step. Alternatively, the nonlinear iterative partial

least squares (NIPALS) algorithm (Geladi, 1986)

can be used to calculate them one at a time in order

of significance.

2.2 Multi-way PCA (MPCA)

Since batch process data is usually arranged in a 3-

way matrix (batch-variable-time), it must be

unfolded into a 2-way matrix in order to apply PCA.

This is known as Multi-way Principal Component

Analysis (MPCA) and was first introduced by Wold

et al. (1987). There are several ways to unfold a 3-

way matrix. In this paper, we choose to unfold the

data along wavelength direction (Fig. 3), because we

are interested in tracking process changes over time.

time

wavelength

wafer1

wafer24

wafer2

time

wavelength

24 wafers

time

Batch

Figure 3: Unfolding of the 3-way OES data blocks. Each

block corresponds to a lot of 24 wafers.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

362

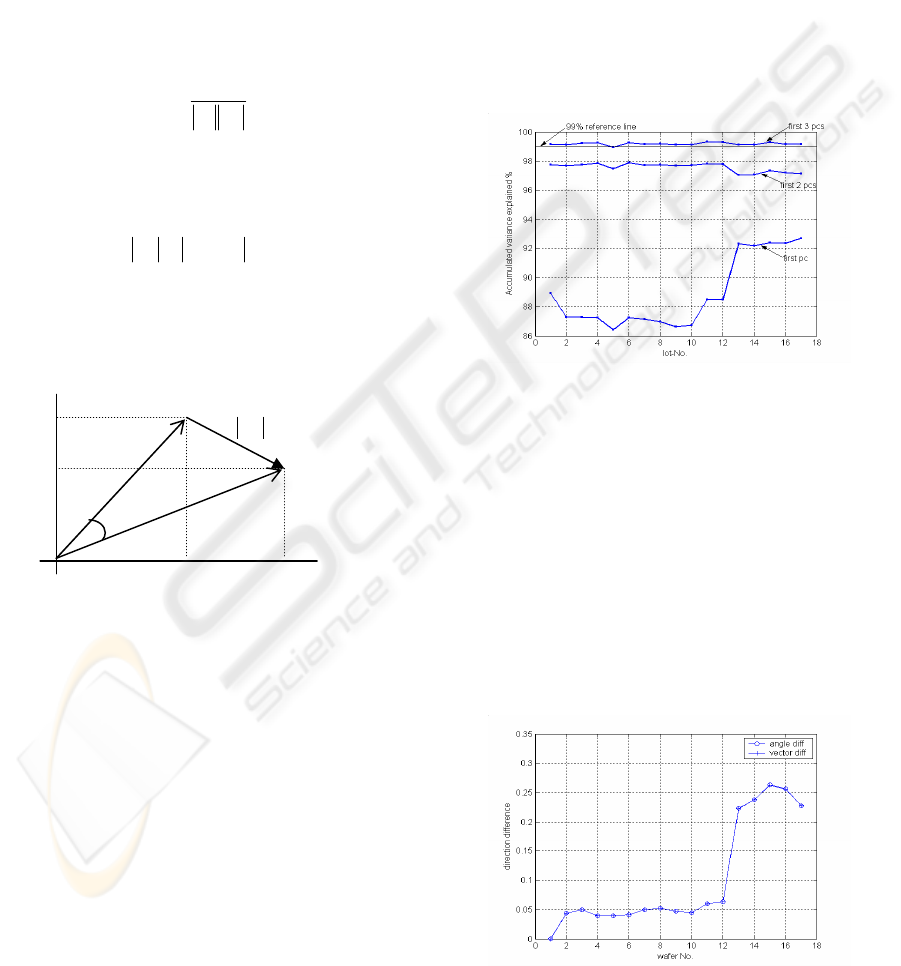
2.3 Monitoring PC-loadings

If PCA is performed on the OES data as a whole

process trends can only be observed by monitoring

the time evolution of the scores. However, if PCA is

applied on a wafer-by-wafer or lot-by-lot basis very

effective monitoring of process variation can be

achieved by tracking the changes in the directions of

the PC loadings. Changes can be expressed either in

terms the angle between loadings or the magnitude

of the vector difference between them as illustrated

in Fig. 4. The angle

θ (in radians) is given by

)

(

arccosθ =

(5)

while the magnitude of the vector difference

φ is

simply defined as

vvΔv −==φ .

(6)

Since, by definition, loading vectors are unit length

it follows that for small

θ the two measures are

approximately equivalent, i.e.

θφ ≈ .

Figure 4: Measuring changes in loading vector directions.

3 OES DATA ANALYSIS

3.1 Data Pre-processing

Data pre-processing is an essential first step in PCA

analysis. Variables need to be appropriately scaled

and irrelevant or corrupted measurements removed

if valid and interpretable results are to be obtained.

In this study the following pre-processing step were

performed on the OES data: (1) Data segments

corresponding to non-etch periods at the start and

end of each etch cycle were removed; (2) Saturated

wavelengths were omitted and; (3) Wavelength

intensities were scaled to have zero mean.

3.2 Lot-by-lot Analysis

Having unfolded the OES data as indicated in Fig. 3,

analysis by PCA can be performed by treating each

lot of 24 wafers as a single data matrix. We will

refer to the resulting PCs as lot-PCs, consisting of

lot-PC loadings and lot-PC scores. The variance

explained by the first three lot-PCs is plotted as a

function of lot number in Fig. 5. This shows that

across all lots the first three principal components

can explain over 99% of the plasma variation

captured by the OES data. In fact the first PC

captures over 85% of the data variation observed

across all 2048 wavelengths.

Figure 5: Accumulated variance explained by the first

three lot PCs.

A closer look at Fig. 5 shows that a jump occurs

in the variance explained by lot-PC

at lot 13.

Analysis of the variation in the direction of lot-PC

across lots (Fig. 6) reveals that this is linked to a

significant change in the orientation of lot-PC

from

lot 13 onwards. Following investigation it was

determined that the plasma change was as a result of

a small drift in the flow rate of a cooling gas applied

to the backside of the wafers during etching, a

change that was not detected by the existing plasma

chamber process monitoring schemes.

Figure 6: Variation in lot-PC

(loading) direction across

lots (with respect to lot 1).

Δv

TRACKING PLASMA ETCH PROCESS VARIATIONS USING PRINCIPAL COMPONENT ANALYSIS OF OES

DATA

363

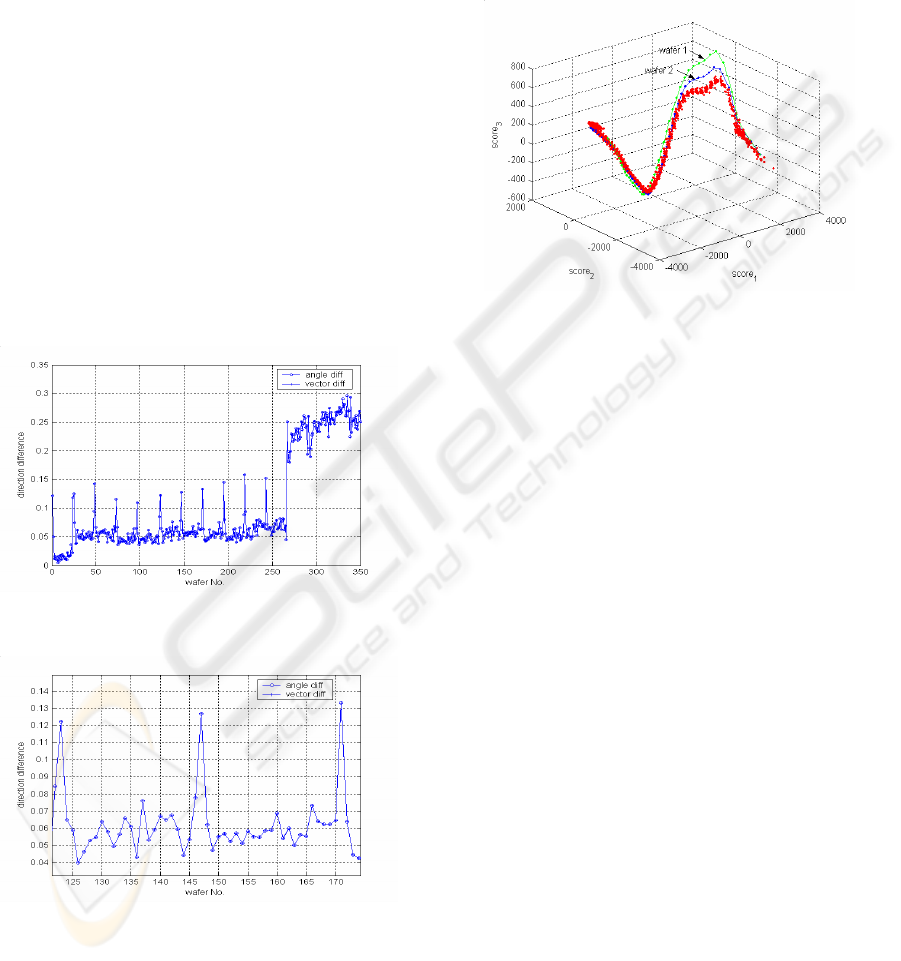
3.3 Wafer-by-wafer Analysis

Here, we simply perform PCA analysis on

individual wafer OES data sets and compare the

patterns across wafers. This allows us to explore the

variation that takes place within lots.

Fig. 7 shows the variation in wafer-PC

direction

over all the wafers with lot-PC

from lot 1 taken as a

reference. The plasma change at lot 12 observed in

the lot-PC analysis is clearly present in this data as

well, as is a small offset during the first lot.

Large spikes are evident throughout Fig. 7.

These occur at the first wafer in each lot. This is

highlighted in Fig. 8 which shows a zoomed in view

of Fig. 7 covering two lots. These sharp changes

were attributed to changes in the absorption

characteristics of the plasma chamber wall as a

result of a cleaning cycle that is performed between

lots. While a dummy etch cycle is performed

following each clean cycle to counter this affect, it is

clear from Fig. 8 that cleaning still has a significant

impact on plasma characteristics for the first (and to

a lesser extent) the second wafer etch of each lot.

Figure 7: Variation in wafer-PC

direction across all

wafers (using lot-PC

from lot 1 as a reference).

Figure 8: Variation in wafer-PC

direction over two lots.

3.4 Score Patterns

As an illustration of the data compression and

pattern visualisation capabilities of PCA the score

patterns generated by the OES data for all the wafers

in lot 9 are plotted in Fig. 9. Here, the first three lot-

PC loadings from lot 8 were used as a reference PC

model and the PC-scores for each wafer calculated

according to Eq. (4). It is easy to see that the

evolution of the OES data for the first and second

wafers is substantially different from the remaining

wafers, as predicted by the wafer-PC loading

analysis.

Figure 9: The first three scores of all the wafers in lot 9.

4 CONCLUSIONS

In this paper we have demonstrated how monitoring

changes in PC directions can be a useful tool in

revealing patterns contained in the high dimensional

data sets generated from OES analysis of wafer etch

plasma chambers.

ACKNOWLEDGEMENTS

The financial support provided by Enterprise Ireland

is gratefully acknowledged.

REFERENCES

Sugawara, M., 1998. Plasma Etching: Fundamentals and

applications, Oxford University Press, New York.

Splichal, M., Anderson, H., 1987. Application of

Chemometrics to Optical Emission Spectroscopy for

Plasma Monitoring. Proc. SPIE, 2, pp. 189-203.

Jackson, J. E., 1991. A User’s Guide to Principal

Components, Wiley Interscience Press, New York.

Geladi, P., Kowalski, R. B., 1986. Partial least-squares

regression: a tutorial. Analytica Chimica. Acta., 185,

pp.1-17.

Wold, S., Geladi, P., Esbensen, K., Ohman, J., 1987.

Multi-way principal components and PLS analysis.

Journal of Chemometrics, 1, pp. 41-56.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

364