
DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL
NEURAL NETWORKS
Krzysztof Patan, J
´
ozef Korbicz and Gracjan Głowacki
Institute of Control and Computation Engineering, University of Zielona G
´
ora
ul. Podg
´
orna 50, 65-246 Zielona G
´
ora, Poland
Keywords:
Neural networks, DC motor, modelling, density shaping, fault detection, fault isolation, fault identification.
Abstract:
The paper deals with a model-based fault diagnosis for a DC motor realized using artificial neural networks.
The considered process was modelled by using a neural network composed of dynamic neuron models. De-
cision making about possible faults was performed using statistical analysis of a residual. A neural network
was applied to density shaping of a residual, and after that, assuming a significance level, a threshold was
calculated. Moreover, to isolate faults a neural classifier was developed. The proposed approach was tested in
a DC motor laboratory system at the nominal operating conditions as well as in the case of faults.
.
1 INTRODUCTION
Electrical motors play a very important role in the
safe and efficient work of modern industrial plants
and processes. An early diagnosis of abnormal and
faulty states renders it possible to perform important
preventing actions and it allows one to avoid heavy
economic losses involved in stopped production, re-
placement of elements or parts (Patton et al., 2000).
To keep an electrical machine in the best condition, a
several techniques like fault monitoring or diagnosis
should be implemented. Conventional DC motors are
very popular, because they are reasonably cheap and
easy to control. Unfortunately, their main drawback
is the mechanical collector which has only a limited
life spam. In addition, brush sparking can destroy the
rotor coil, generate EMC problems and reduce the in-
sulation resistance to an unacceptable limit (Moseler
and Isermann, 2000). Moreover, in many cases elec-
trical motors operate in the closed-loop control, and
small faults often remain hidden by the control loop.
Only if the whole device fails the failure becomes vis-
ible. Therefore, there is a need to detect and isolate
faults as early as possible.
Recently, a great deal of attention has been paid
to electrical motor fault diagnosis (Moseler and Is-
ermann, 2000; Xiang-Qun and Zhang, 2000; Fues-
sel and Isermann, 2000). In general, elaborated solu-
tions can be splitted into three categories: signal anal-
ysis methods, knowledge-based methods and model-
based approaches (Xiang-Qun and Zhang, 2000; Ko-
rbicz et al., 2004). Methods based on signal anal-
ysis include vibration analysis, current analysis, etc.
The main advantage of these approaches is that accu-
rate modelling of a motor is avoided. However, these
methods only use output signals of a motor, hence the
influence of an input on an output is not considered.
In turn, the frequency analysis is time-consuming,
thus it is not proper for on-line fault diagnosis. In the
case of vibration analysis there are serious problems
with noise produced by environment and coupling of
sensors to the motor (Xiang-Qun and Zhang, 2000).
Knowledge-based approaches are generally based
on expert or qualitative reasoning (Zhang and Ellis,
1991). Several knowledge based fault diagnosis ap-
proaches have been proposed. These include the rule-
based approaches where diagnostic rules can be for-
mulated from process structure and unit functions,
and the qualitative simulation-based approaches. The
trouble with the use of such models is that accumulat-
ing experience and expressing it as knowledge rules
is difficult and time-consuming. Therefore, develop-
ment of a knowledge-based diagnosis system is gen-
erally effort demanding.
Model-based approaches include parameter esti-
mation, state estimation, etc. This kind of methods
can be effectively used to on-line diagnosis, but its
disadvantage is that an accurate model of a motor is
required (Korbicz et al., 2004). An alternative so-
lution can be obtained through artificial intelligence,
e.g. neural networks. The self-learning ability and
property of modelling nonlinear systems allow one to
employ neural networks to model complex, unknown
and nonlinear dynamic processes (Frank and K
¨
oppen-
11
Patan K., Korbicz J. and Głowacki G. (2007).
DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 11-18
DOI: 10.5220/0001625400110018
Copyright
c
SciTePress

Seliger, 1997).
The paper is organized as follows. First, descrip-
tion of the considered DC motor is presented in Sec-
tion 2. The model-based fault diagnosis concept is
discussed in Section 3. The architecture details of the
dynamic neural network used as a model of the DC
motor is given in Section 4. Next, a density shaping
technique used to fault detection and a neural classi-
fier applied to isolation of faults are explained in Sec-
tion 5. Section 6 reports experimental results.
2 AMIRA DR300 LABORATORY
SYSTEM
The AMIRA DR300 laboratory system shown in
Fig. 1 is used to control the rotational speed of a DC
motor with a changing load. The considered labora-
tory object consists of five main elements: the DC
motor M1, the DC motor M2, two digital increamen-
tal encoders and the clutch K. The input signal of the
engine M1 is an armature current and the output one
is the angular velocity. Available sensors for the out-
put are an analog tachometer on optical sensor, which
generates impulses that correspond to the rotations of
the engine and a digital incremental encoder. The
shaft of the motor M1 is connected with the identical
motor M2 by the clutch K. The second motor M2 op-
erates in the generator mode and its input signal is an
armature current. Available measuremets of the plant
are as follows:
• motor current I
m
– the motor current of the DC
motor M1,
• generator current I
g
– the motor current of the DC
motor M2,
• tachometer signal T ,
and control signals:
• motor control signal C
m
– the input of the motor
M1,
Figure 1: Laboratory system with a DC motor.
Table 1: Laboratory system technical data.
Variable Value
Motor
rated voltage 24 V
rated current 2 A
rated torque 0.096 Nm
rated speed 3000 rpm
voltage constant 6.27 mV/rpm
moment of inertia 17.7 × 10
−6
Kgm
2
torque constant 0.06 Nm/A
resistance 3.13 Ω
Tachometer
output voltage 5 mV/rpm
moment of interia 10.6 × 10
−6
Kgm
2
Clutch
moment of inertia 33 × 10
−6
Kgm
2
Incremental encoder
number of lines 1024
max. resolution 4096/R
moment of inertia 1.45 × 10
−6
Kgm
2
• generator control signal C
g
– the input of the mo-
tor M2.
The technical data of the laboratory system is pre-
sented in Table 1. The separately excited DC motor is
governed by two differential equations. The electrical
subsystem can be described by the equation:
u(t) = Ri(t) + L
di(t)
dt
+ e(t) (1)
where u(t) is the motor armature voltage, R – the ar-
mature coil resistance, i(t) – the motor armature cur-
rent, L – the motor coil inductance, and e(t) – the
induced electromotive force. The induced electromo-
tive force is proportional to the angular velocity of the
motor: e(t) = K
e
ω(t), where K
e
stands for the motor
voltage constant and ω(t) – the angular velocity of
the motor. In turn, the mechanical subsystem can be
derived from the torque balance:
J
dω(t)
dt
= T
m
(t) − B
m
ω(t) − T
l
− T
f
(ω(t)) (2)
where J is the motor moment of inertia, T
m
– the mo-
tor torque, B
m
– the viscous friction torque coeffi-
cient, T
l
– the load torque, and T
f
(ω(t)) – the friction
torque. The motor torque T
m
(t) is proportional to the
armature current: T
m
(t) = K
m
i(t), where K
m
stands
for the motor torque constant. The friction torque
can be considered as a function of angular velocity
and it is assumed to be the sum of Stribeck, Coulumb
and viscous components. The viscous friction torque
opposes motion and it is proportional to the angular
velocity. The Coulomb friction torque is constant at
any angular velocity. The Stribeck friction is a non-
linear component occuring at low angular velocities.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
12

The model (1)-(2) has a direct relation to the motor
physical parameters, however, the relation between
them is nonlinear.There are many nonlinear factors in
the motor, e.g. the nonlinearity of the magnetization
chracteristic of material, the effect of material reac-
tion, the effect caused by eddy current in the mag-
net, the residual magnetism, the commutator charac-
teristic, mechanical frictions (Xiang-Qun and Zhang,
2000). Summarizing, a DC motor is a nonlinear dy-
namic process.
3 MODEL-BASED FAULT
DIAGNOSIS
Model-based approaches generally utilise results
from the field of control theory and are based on pa-
rameter estimation or state estimation (Patton et al.,
2000; Korbicz et al., 2004). When using this ap-
proach, it is essential to have quite accurate models of
a process. Generally, fault diagnosis procedure con-
sists of two separate stages: residual generation and
residual evaluation. The residual generation process
is based on a comparison between the output of the
system and the output of the constructed model. As
a result, the difference or so-called residual r is ex-
pected to be near zero under normal operating con-
ditions, but on the occurrence of a fault, a deviation
from zero should appear. Unfortunately, designing
mathematical models for complex nonlinear systems
can be difficult or even impossible. For the model-
based approach, the neural network replaces the an-
alytical model that describes the process under nor-
mal operating conditions (Frank and K
¨
oppen-Seliger,
1997). First, the network has to be trained for this
task. Learning data can be collected directly from the
process, if possible or from a simulation model that is
as realistic as possible. Training process can be car-
ried out off-line or on-line (it depends on availability
of data). After finishing the training, a neural network
is ready for on-line residual generation. In order to
be able to capture dynamic behaviour of the system, a
neural network should have dynamic properties, e.g.
it should be a recurrent network (Korbicz et al., 2004;
Patan and Parisini, 2005). In turn, the residual evalua-
tion block transforms the residual r into the fault vec-
tor f in order to determine the decision about faults,
their location and size, and time of fault occurence.
In general, there are three phases in the diagnos-
tic process: detection, isolation and identification of
faults (Patton et al., 2000; Korbicz et al., 2004). In
practice, however, the identification phase appears
rarely and sometimes it is incorporated into fault iso-
lation. Thus, from practical point of view, the diag-
nostic process consists of two phases only: fault de-
tection and isolation. The main objective of fault de-
tection is to make a decision whether a fault occur
or not. The fault isolation should give an information
about fault location. Neural networks can be very use-
full in designing the residual evaluation block. In the
following sections some solutions for realization fault
detection and isolation are discussed.
4 DYNAMIC NEURAL NETWORK
Let us consider the neural network described by the
following formulae:
ϕ
1
j
(k) =
n
∑
i=1
w
1
ji
u
i
(k) (3)
z
1
j
(k) =
r
1
∑
i=0
b
1
ji
ϕ
1
j
(k − i) −
r
1
∑
i=1
a
1
ji
z
1
j
(k − i) (4)
y
1
j
(k) = f (z
1
j
(k)) (5)
ϕ
2
j
(k) =
v
1
∑
i=1
w
2
ji
y
1
i
(k) +
n
∑
i=1
w
u
ji
u
i
(k) (6)
y
2
j
(k) = −
r
2
∑
i=1
a
2
ji
y
1
j
(k − i) (7)
y
j
(k) =
v
2
∑
i=1
w
3
ji
y
2
j
(k) (8)
where w
1
ji
, j = 1,..., v
1
are the input weights, w
2
ji
,
j = 1, .. .,v
2
– the weights between the output and the
first hidden layers, w
3
ji
, j = 1, ... ,m – the weights be-
tween the output and the second hidden layers, w
u
ji
,
j = 1, ... ,v
2
– the weights between output and input
layers, ϕ
1
j
(k) and ϕ
2
j
(k) are the weighted sums of in-
puts of the j-th neuron in the hidden and output lay-
ers, respectively, u
i
(k) are the external inputs to the
network, z
1
j
(k) is the activation of the j-th neuron in
the first hidden layer, a
1
ji
and a
2
ji
are feedback filter
parameters of the j-th neuron in the first and second
hidden layers, respectively, b
1
ji
are the feed-forward
filter parameters of the j-th neuron of the first hidden
layer, f (·) – nonlinear activation function, y
1
j
(k) and
y
2
j
(k) – the outputs of the j-th neuron of the first and
second hidden layers, respectively, and finally y
j
(k),
j = 1, ... ,v
2
are the network ouputs. The structure
of the network is presented in Fig. 2. The first hid-
den layer consists of v
1
neurons with infinite impulse
response filters of the order r
1
and nonlinear activa-
tion functions. The second hidden layer consists of
v
2
neurons with finite impulse response filters of the
order r
2
and linear activation functions. Neurons of
this layer receive excitation not only from the neu-
DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS
13
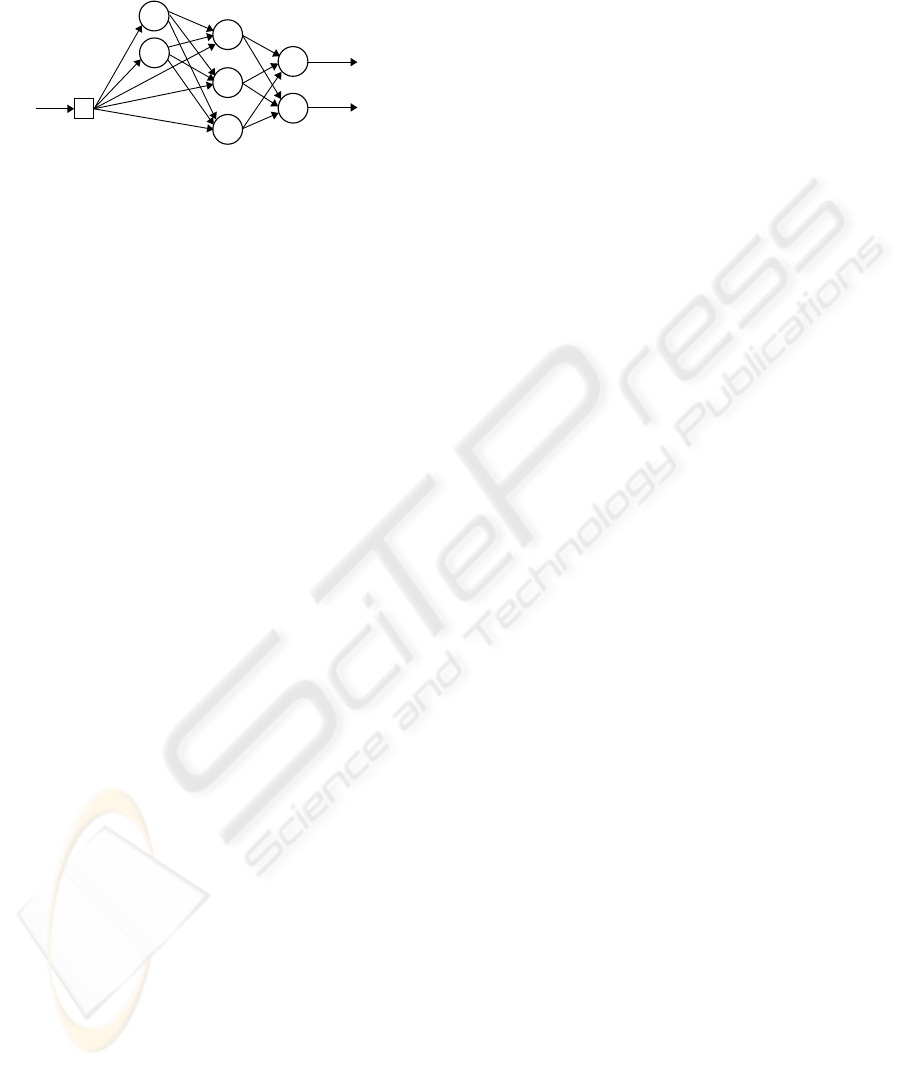
l
IIR – neuron with IIR filter
l
FIR – neuron with FIR filter
l
L – static linear neuron
W
u
W
1
W
2
W
3
u(k)
y
1
(k)
y
2
(k)
FIR
FIR
FIR
IIR
IIR
L
L
Figure 2: The cascade structure of the dynamic neural net-
work.
rons of the hidden layer but also from the external in-
puts (Fig. 2). Finaly, the network output is produced
by the linear output layer. The network structure (3)-
(8) is not a strict feed-forward one. It has a cascade
structure. Detailed analysis of this network and its ap-
proximation abilities are given in paper (Patan, 2007).
Introduction of an additional weight matrix W
u
ren-
ders it possible to obtain a system, in which the whole
state vector is available from the neurons of the out-
put layer. In this way, the proposed neural model can
produce a state vector at its output and can serve as
a nonlinear observer. This fact is of a crucial impor-
tance taking into account training of the neural net-
work. Moreover, this neural structure has similar ap-
proximation abilities as a locally recurrent globally
feedforward network with two hidden layers designed
using nonlinear neuron models with IIR filters, while
the number of adaptable parameters is significantly
lower (Patan, 2007).
4.1 Network Training
All unknown network parameters can be represented
by a vector θ. The objective of training is to find the
optimal vector of parameters θ
?
by minimization of
some loss (cost) function:
θ
?
= arg
θ∈C
min J(θ) (9)
where J : R
p
→ R represents some loss function to be
minimized, p is the dimension of the vector θ, and
C ⊆ R
p
is the set of admissible parameters consti-
tuted by constraints. To minimize (9) one can use the
Adaptive Random Search algorithm (ARS) (Walter
and Pronzato, 1996). Assuming that the sequence of
solutions
ˆ
θ
0
,
ˆ
θ
1
,.. .,
ˆ
θ
k
is already appointed, the next
point
ˆ
θ
k+1
is calculated as follows (Walter and Pron-
zato, 1996):
ˆ
θ
k+1
=
ˆ
θ
k
+ r
k
(10)
where
ˆ
θ
k
is the estimate of the θ
?
at the k-th itera-
tion, and r
k
is the perturbation vector generated ran-
domly according to the normal distribution N (0,σ).
The new point
ˆ
θ
k+1
is accepted when the cost func-
tion J(
ˆ
θ
k+1
) is lower than J(
ˆ
θ
k
) otherwise
ˆ
θ
k+1
=
ˆ
θ
k
.
To start the optimization procedure, it is necessary to
determine the initial point
ˆ
θ
0
and the variance σ. Let
θ
?
be a global minimum to be located. When
ˆ
θ
k
is far
from θ
?
, r
k
should have a large variance to allow large
displacements, which are necessary to escape the lo-
cal minima. On the other hand, when
ˆ
θ
k
is close θ
?
,
r
k
should have a small variance to allow exact explo-
ration of parameter space. The idea of the ARS is to
alternate two phases: variance-selection and variance-
exploitation (Walter and Pronzato, 1996). During the
variance-selection phase, several successive values of
σ are tried for a given number of iteration of the basic
algorithm. The competing σ
i
is rated by their perfor-
mance in the basic algorithm in terms of cost reduc-
tion starting from the same initial point. Each σ
i
is
computed according to the formula:
σ
i
= 10
−i
σ
0
, for i = 1, ... ,4 (11)
and it is allowed for 100/i iterations to give more
trails to larger variances. σ
0
is the initial variance and
can be determined, e.g. as a spread of the parameters
domain:
σ
0
= θ
max
− θ
min
(12)
where θ
max
and θ
min
are the largest and lowest pos-
sible values of parameters, respectively. The best σ
i
in terms the lowest value of the cost function is se-
lected for the variance-exploitation phase. The best
parameter set
ˆ
θ
k
and the variance σ
i
are used in the
variance-exploitation phase, whilst the algorithm (10)
is run typically for one hundred iterations. The algo-
rithm can be terminated when the maximum number
of algorithm iteration n
max
is reached or when the as-
sumed accuracy J
min
is obtained. Taking into account
local minima, the algorithm can be stopped when σ
4
has been selected a given number of times. It means
that algorithm got stuck in a local minimum and can-
not escape its basin of attraction. Apart from its sim-
plicity, the algorithm possesses the property of global
convergence. Moreover, adaptive parameters of the
algorithm, cause that a chance to get stuck in local
minima is decreased.
5 NEURAL NETWORKS BASED
DECISION MAKING
5.1 Fault Detection
In many cases, the residual evaluation is based on the
assumption that the underlying data is normally dis-
tributed (Walter and Pronzato, 1996). This weak as-
sumption can cause inaccurate decision making and a
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
14

number of false alarms can be considerable. Thus,
in order to select a threshold in a proper way, the
distribution of the residual should be discovered or
transformation of the residual to another known dis-
tribution should be performed. A transformation of a
random vector x of an arbitrary distribution to a new
random vector y of different distribution can be re-
alized by maximazing the output entropy of the neu-
ral network (Haykin, 1999; Roth and Baram, 1996;
Bell and Sejnowski, 1995). Let us consider a situ-
ation when a single input is passed through a trans-
forming function f (x) to give an output y, where f (x)
is monotonically increasing continuous function sat-
isfying lim
x→+∞
f (x) = 1 and lim
x→−∞
f (x) = 0. The
probability density function of y satisfies
p
y
(y) =
p
x
(x)
|∂y/∂x|
(13)
The entropy of the output h(y) is given by
h(y) = −E{log p
y
(y)} (14)
where E{·} stands for the expected value. Substitut-
ing (13) into (14) it gives
h(y) = h(x) + E
log
∂y
∂x
(15)
The first term on the right can be considered to be un-
affected by alternations in parameters of f (x). There-
fore, to maximize the entropy of y one need to take
into account the second term only.
Let us define the divergence between two density
functions as follows
D(p
x
(x),q
x
(x)) = E
log
p
x
(x)
q
x
(x)
(16)
finally one obtains
h(y) = −D(p
x
(x),q
x
(x)) (17)
where q
x
(x) = |∂(y)/∂(x)|. The divergence between
true density of x (p
x
(x)) and an arbitrary one q
x
(x) is
minimized when entropy of y is maximized. The in-
put probability density function is then approximated
by |∂y/∂x|. The simple and elegant way to adjust net-
work parameters in order to maximize the entropy of
y was given in (Bell and Sejnowski, 1995). They used
the on-line version of stochastic gradient ascent rule
∆w=
∂h(y)
∂w
=
∂
∂w
log
∂y
∂x
=
∂y
∂x
−1
∂
∂w
∂y
∂x
(18)
Considering the logistic transfer function of the
form:
y =
1
1 + exp (−u)
, u = wx + b (19)
f (·)
y
− +
+
×
1b
w +
ˆq(x)
w
1
x u
Figure 3: Neural network for density calculation.
where w is the input weight and b is the bias weight,
and applying (18) to (19) finally one obtains
∆w =
1
w
+ x(1 + 2y) (20)
Using a similar reasoning, a rule for the bias weight
parameter can be derived
∆b = 1 − 2y (21)
After training, the estimated probability density func-
tion can be calculated using scheme shown in Fig. 3.
In this case, an output threshold of the density shap-
ing scheme (Fig. 3) can be easily calculated by the
formula:
T
q
= |0.5α(1 − 0.5α)w| (22)
where α is the confidence level.
5.2 Fault Isolation
Transformation of the residual r into the fault vector
f can be seen as a classification problem. For fault
isolation, it means that each pattern of the symptom
vector r is assigned to one of the classes of system be-
haviour { f
0
, f
1
, f
2
,.. ., f
n
}. To perform fault isolation,
the well-known static multi-layer perceptron network
can be used. In fact, the neural classifier should map
a relation of the form Ψ : R
n
→ R
m
: Ψ(r) = f.
5.3 Fault Identification
When analytical equations of residuals are unknown,
the fault identification consists in estimating the fault
size and time of fault occurence on the basis of resid-
ual values. An elementary index of the residual size
assigned to the fault size is the ratio of the residual
value r
j
to suitably assigned threshold value T
j
. This
threshold can be calculated using (22). In this way,
the fault size can be represented as the mean value of
such elementary indices for all residuals as follows:
s( f
k
) =
1
N
∑
j:r
j
∈R( f
k
)
r
j
T
j
(23)
where s( f
k
) represents the size of the fault f
k
, R( f
k
)
– the set of residuals sensitive to the fault f
k
, N – the
size of the set R( f
k
).
DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS
15
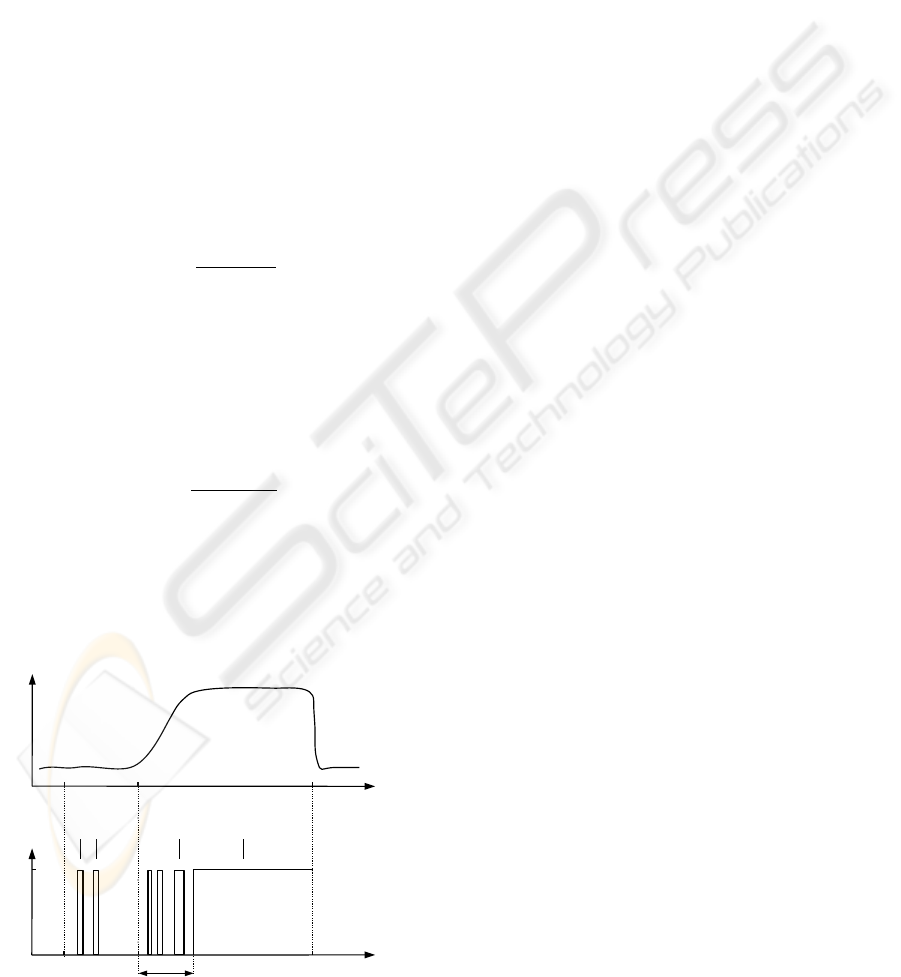
5.4 Evaluation of the Fdi System
The benchmark zone is defined from the benchmark
start-up time t
on
to the benchmark time horizon t
hor
(Fig. 4). Decisions before the benchmark start-up t
on
and after the benchmark time horizon t
hor
are out of
interest. The time of fault start-up is represented by
t
f rom
. When a fault occurs in the system, a residual
should deviate from the level assigned to the fault-free
case (Fig. 4). The quality of the fault detection sys-
tem can be evaluated using a number of performance
indexes (Patan and Parisini, 2005):
• Time of fault detection t
dt
– a period of time
needed for detection of a fault measured from
t
f rom
to a permanent, true decision about a fault,
as presented in Fig. 4. As one can see there, the
first three true decisions are temporary ones and
are not taken into account during determining t
dt
.
• False detection rate r
f d
:
r
f d
=
∑
i
t
i
f d
t
f rom
−t
on
, (24)
where t
i
f d
is the period of i-th false fault detection.
This index is used to check the system in the fault-
free case. Its value shows a percentage of false
alarms. In the ideal case (no false alarms) its value
should be equal to 0.
• True detection rate r
td
:
r
td
=
∑
i
t
i
td
t
hor
−t
f rom
, (25)
where t
i
td
is the period of i-th true fault detection.
This index is used in the case of faults and de-
scribes efficiency of fault detection. In the ideal
case (fault detected immediately and surely) its
value is equal to 1.
t
on
t
f rom
t
hor
time
time
t
dt
residualfault decision
0
1
true decisions
false
decisions
? ???
Figure 4: Illustration of performance indexes.
6 EXPERIMENTS
The motor described in Section 2 works is a closed
loop control with the PI controller. It is assumed that
load of the motor is equal to 0. The objective of the
system control is to keep the rotational speed at the
constant value equal to 2000. Additionally, it is as-
sumed that the reference value is corrupted by addi-
tive noise.
6.1 Motor Modelling
A separately excited DC motor was modelled by us-
ing dynamic neural network presented in Section 4.
The model of the motor was selected as follows:
T = f (C
m
) (26)
The following input signal was used in experiments:
C
m
(k) = 3 sin(2π0.017k) + 3sin(2π0.011k − π/7)
+ 3 sin(2π0.003k + π/3)
(27)
The input signal (27) is persistantly exciting of the or-
der 6. Using (27) a learning set containig 1000 sam-
ples was formed. The neural network model (3)-(8)
had the following structure: one input, 3 IIR neurons
with the first order filters and hyperbolic tangent ac-
tivation functions, 6 FIR neurons with the first order
filters and linear activation functions, and one linear
output neuron. Training process was carried out for
100 steps using the ARS algorithm with initial vari-
ance σ
0
= 0.1. The outputs of the neural model and
separately excited motor generated for another 1000
testing samples are depicted in Fig. 5. The efficiency
of the neural model was also checked during the work
of the motor in the closed-loop control. The results
are presented in Fig. 6. After transitional oscilations,
the neural model settled at a proper value. This gives
a strong argument that neural model mimics the be-
haviour of the DC motor pretty well.
6.2 Fault Detection
Two types of faults were examined during experi-
ments:
• f
1
i
– tachometer faults were simulated by increas-
ing/decreasing rotational speed by ±25%, ±10%
and ±5%,
• f
2
i
– mechanical faults were simulated by increas-
ing/decreasing motor torque by ±40%, ±20%.
In result, a total of 10 faulty situation were investi-
gated. Using the neural model of the process, a resid-
ual signal was generated. This signal was used to
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
16
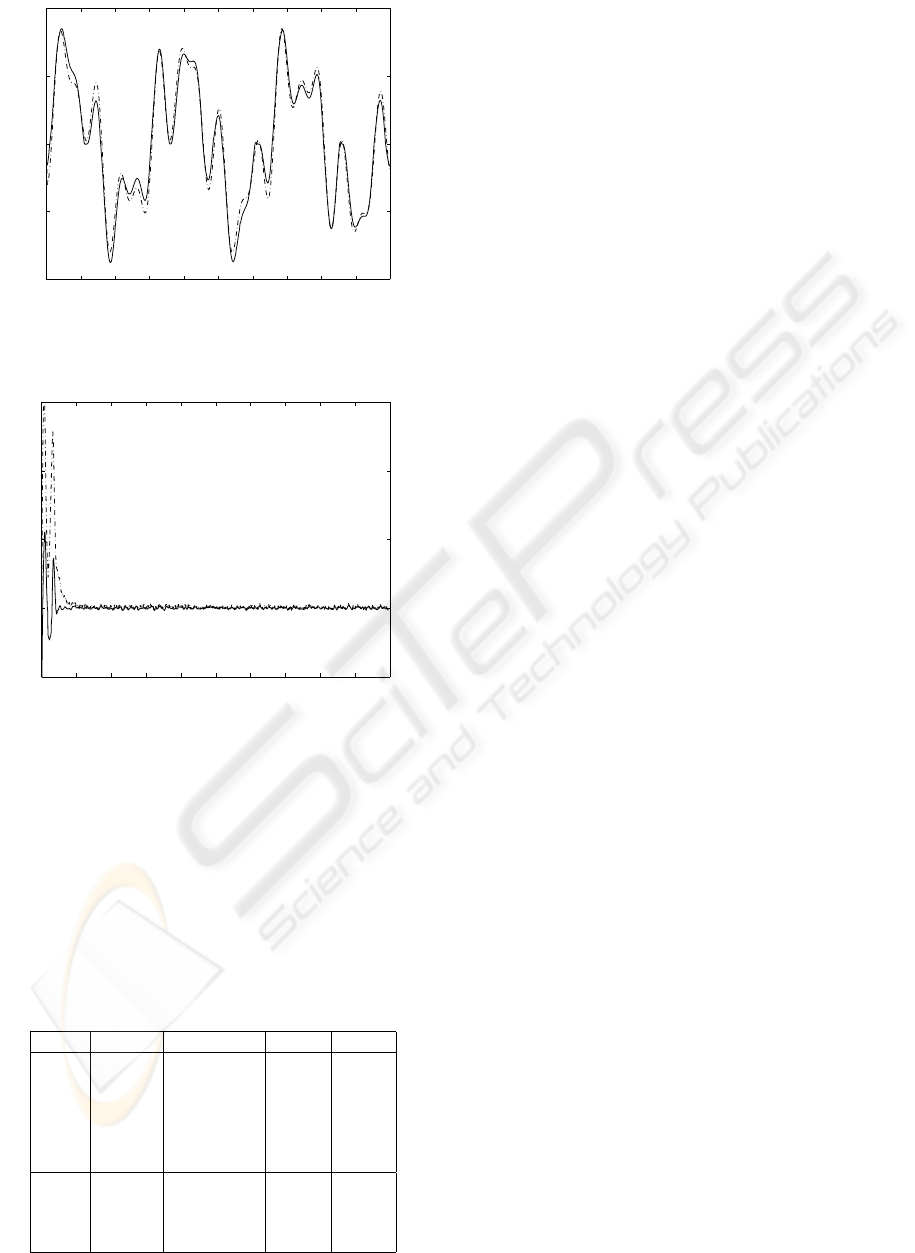
0 100 200 300 400 500 600 700 800 900 1000
−4000
−2000
0
2000
4000
time
rotational speed
Figure 5: Responses of the motor (solid) and neural model
(dash-dot) – open-loop control.
0 200 400 600 800 1000 1200 1400 1600 1800 2000
1000
2000
3000
4000
5000
time
rotational speed
Figure 6: Responses of the motor (solid) and neural model
(dash-dot) – closed-loop control.
train another neural network to approximate a prob-
ability density function of the residual. Training pro-
cess was carried out on-line for 100000 steps using
unsupervised learning described in Section 5.1. The
final network parameters were: w = −711,43 and
b = −1.26. Cut off values determined for significance
Table 2: Performance indices.
Fault r
td
t
dt
R [%] s
f
1
1
0.9995 2035 99 19.51
f
1
2
0.9995 2000 82 12.60
f
1
3
0.9988 2097 56 5.78
f
1
4
0.9395 2086 84 5.45
f
1
5
0.9923 2142 62 4.07
f
1
6
0.5245 undetected 54 1.48
f
2
1
0.9998 2005 100 52.69
f
2
2
1.0 2000 100 29,24
f
2
3
0.9997 2005 96 27.30
f
2
4
0.9993 2008 97 14.56
level α = 0.05 had values x
l
= −0.007 and x
r
= 0,003
and the threshold was equal to T = 17, 341. In order
to perform decision about faults, and to determine de-
tection time t
dt
, a time window with the length n = 50
was used. If during the following n time steps the
residual exceeded the threshold then a fault was sig-
nalled. Application of time-window prevents the sit-
uation when a temporary true detection will signal a
fault (see Fig. 4). The results of fault detection are
presented in the second and third columns of Table 2.
All faults were reliably detected except fault f
1
6
. In
this case, the changes simulated on tachometer sensor
were poorly observed in the residual.
6.3 Fault Isolation
Fault isolation can be considered as a classification
problem where a given residual value is assigned to
one of the predefined classes of system behaviour. In
the case considered here, there is only one residual
signal and 10 different faulty scenarios. To perform
fault isolation the well-known multilayer perceptron
was used. The neural network had one input (residual
signal) and 4 outputs (each class of system behaviour
was coded using 4-bit representation). The learning
set was formed using 100 samples per each faulty
situation and 100 samples representing the fault-free
case, then the size of the learning set was equal to
1100. As the well performing neural classifier, the
network with 15 hyperbolic tangent neurons in the
first hidden layer, 7 hyperbolic tangent neurons in the
second hidden layer, and 4 sigmoidal output neurons
was selected. The neural classifier was trained for 500
steps using the Levenberg-Marquardt method. Addi-
tionally, the real-valued response of the classifier was
transformed to the binary one. The simple idea is to
calculate a distance between the classifier output and
each predefined class of system behaviour. As a re-
sult, a binary representation giving the shortest dis-
tance is selected as a classifier binary output. This
transformation can be represented as follows:
j = arg min
i
||x − K
i
||, i = 1, ... ,N
K
(28)
where x is the real-valued output of the classifier, K
i
–
the binary representation of the i-th class, N
K
– the
number of predefined classes of system behaviour,
and || · || – the Euclidean distance. Then, the binary
representation of the classifier can be determined in
the form ¯x = K
j
. Recognition accuracy (R) results are
presented in the fourth column of Table 2. The worst
results 56% and 62% were obtained for the faults f
1
3
and f
1
6
, respectively. The fault f
1
3
was frequently rec-
ognized as the fault f
1
5
. In spite of misrecognizing,
this fault was detected as a faulty situation. Quite dif-
ferent situation was observed for the classification of
DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS
17

fault f
1
6
. This fault, in majority of cases, was classi-
fied as the normal operating conditions, thus it cannot
be either detected or isolated properly.
6.4 Fault Identification
In this work, the objective of fault identification was
to estimate the size of detected and isolated faults.
The sizes of faults were calculated using (23). The
results are shown in the last column of Table 2. Ana-
lyzing results, one can observe that quite large values
were obtained for the faults f
2
1
, f
2
2
and f
2
3
. That
is the reason that for these three faults true detection
rate and recognition accuracy had maximum or close
to maximum values. Another group is formed by the
faults f
1
1
, f
1
2
and f
2
4
possessing the similar values
of the fault size. The third group of fault consists of
f
1
3
, f
1
4
, and f
1
5
. The fault sizes in these cases are
distinctly smaller than in the cases already discussed.
Also the detection time t
dt
is relatively longer. In spite
of the fact that f
1
6
was not detected, the size of this
fault was also calculated. As one can see the fault size
in this case is very small, what explains the problems
with its detection and isolation.
7 FINAL REMARKS
In the paper, the neural network based method for the
fault detection and isolation of faults in a DC motor
was proposed. Using the novel structure of dynamic
neural network, quite accurate model of the motor
was obtained what rendered it possible detection, iso-
lation or even identification of faults. The approach
was successfully tested on a number of faulty scenar-
ios simulated in the real plant. The achieved results
confirm usefullness and effectiveness of neural net-
works in designing fault detection and isolation sys-
tems. It should be pointed out that presented solution
can be easily applied to on-line fault diagnosis.
ACKNOWLEDGEMENTS
This work was supported in part by the Ministry of
Science and Higher Education in Poland under the
grant Artificial Neural Networks in Robust Diagnostic
Systems
G. Głowacki is a stypendist of the Integrated Re-
gional Operational Programme (Measure 2.6: Re-
gional innovation strategies and the transfer of knowl-
edge) co-financed from the European Social Fund.
REFERENCES
Bell, A. J. and Sejnowski, T. J. (1995). An information-
maximization approach to blind separation and blind
deconvolution. Neural computation, 7:1129–1159.
Frank, P. M. and K
¨
oppen-Seliger, B. (1997). New devel-
opments using AI in fault diagnosis. Artificial Intelli-
gence, 10(1):3–14.
Fuessel, D. and Isermann, R. (2000). Hierarchical motor
diagnosis utilising structural knowledge and a self-
learning neuro-fuzzy scheme. IEEE Trans. Industrial
Electronics, 47:1070–1077.
Haykin, S. (1999). Neural Networks. A comprehensive
foundation, 2nd Edition. Prentice-Hall, New Jersey.
Korbicz, J., Ko
´
scielny, J. M., Kowalczuk, Z., and Cholewa,
W., editors (2004). Fault Diagnosis. Models, Artificial
Intelligence, Applications. Springer-Verlag, Berlin.
Moseler, O. and Isermann, R. (2000). Application of model-
based fault detection to a brushless dc motor. IEEE
Trans. Industrial Electronics, 47:1015–1020.
Patan, K. (2007). Approximation ability of a class of locally
recurrent globally feedforward neural networks. In
Proc. European Control Conference, ECC 2007, Kos,
Greece. accepted.
Patan, K. and Parisini, T. (2005). Identification of neural
dynamic models for fault detection and isolation: the
case of a real sugar evaporation process. Journal of
Process Control, 15:67–79.
Patton, R. J., Frank, P. M., and Clark, R. (2000). Issues
of Fault Diagnosis fo r Dynamic Systems. Springer-
Verlag, Berlin.
Roth, Z. and Baram, Y. (1996). Multidimensional density
shaping by sigmoids. IEEE Trans. Neural Networks,
7(5):1291–1298.
Walter, E. and Pronzato, L. (1996). Identification of Para-
metric Models from Experimental Data. Springer,
London.
Xiang-Qun, L. and Zhang, H. Y. (2000). Fault detection
and diagnosis of permanent-magnet dc motor based
on parameter estimation and neural network. IEEE
Trans. Industrial Electronics, 47:1021–1030.
Zhang, J., P. D. R. and Ellis, J. E. (1991). A self-learning
fault diagnosis system. Transactions of the Institute of
Measurements and Control, 13:29–35.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
18
