
THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR
INTELLIGENT AUTONOMOUS AGENTS HIERARCHICAL
CONTROL STRATEGIES MODELING
Eliezer Arantes da Costa and Celso Pascoli Bottura
LCSI – FEEC - UNICAMP – Cidade Universitária Zeferino Vaz, Campinas, SP, Brazil
Keywords: Autonomous agents, competitive games, cooperative games, distributed intelligent control, hierarchical
architectures, hierarchical control, multiple agent control, Strategic Games Matrix, strategies modeling.
Abstracts: This paper presents a framework for strategy formulation in multilevel multiple-agent control system
architectures based on the Strategic Games Matrix (SGM), having game theory and control systems theory
as basic concepts and models. New methodologies for analysis and for design of hierarchical control
architectures with multiple intelligent autonomous agents, based on the SGM concept, are applied.
Illustrative hierarchical control applications to system architectures analysis and synthesis based on the
SGM are presented.
1 INTRODUCTION
The study of hierarchical multi-agent control
systems is receiving growing attention within the
control community. Driving applications of multiple
agents control include: mobile robots coordination
and control, satellite clusters, automated highways,
unmanned aerial vehicles (UAV), distributed
artificial intelligence, and strategic planning in
general.
A wide diversity of multi-controller and
coordination problems has been treated recently,
e.g., multiple mobile agents moving coordination
and control (Shi, Wang and Chu, 2005), traffic
congestion control (Alpcan and Başar, 2002),
multiple mobile robot control (Shao, Xie, Yu and
Wang, 2005), collision avoidance scheme in
navigation control (Dimaragonas and
Kyriakopoulus, 2005), secure routing in
communication networks (Bohacek, Hespanha and
Obraczka, 2002), optimal bidding strategies in the
electricity market (Rahimi-Kian, Tabarraei and
Sadeghi, 2005), automa-teams coordination and
control (Liu, Galati and Simaan, 2004), attack and
deception strategies in military operations
(Castañón, Pachter and Chandler, 2004), and
intrusion detection in access control systems
(Alpcan and Başar, 2004).
Mathematical approaches used in these papers
treat the control problems as Nash, Pareto,
Stackelberg, Minimax games, or some variations of
them, in an insulated manner.
The formulation of optimal strategies in
competitive and/or cooperative environments has
constituted one of the main challenges for
researchers and scholars (Schelling, 1960;
Brandenburger and Nalebuff, 1995; and Bottura and
Costa, 2004) and a wide variety of approaches has
been proposed and used (Başar and Older, 1999;
Costa F
o
., 1992; and Cruz Jr., 1978). However, a
structured combination of all these possible
approaches on the same hierarchical architecture
should be conceived, formulated, and should have its
usefulness exhibited. Here, an integrated framework
considering these classical games on the same
analytical structure, by going a step further on the
traditional approach used in papers like the above
mentioned, is presented.
In this paper, an ‘agent’ represents a controller, a
decision-maker, a commander, an autonomous
robot, a player – person or team –, software, a
policy-maker, a UAV, a stakeholder, or any human
being. Our approach treats hierarchical, non-
hierarchical, or heterarchical architectures as a
structured collections of sub-games.
184
Arantes da Costa E. and Pascoli Bottura C. (2007).
THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS HIERARCHICAL CONTROL STRATEGIES
MODELING.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 184-189
DOI: 10.5220/0001625001840189
Copyright
c
SciTePress
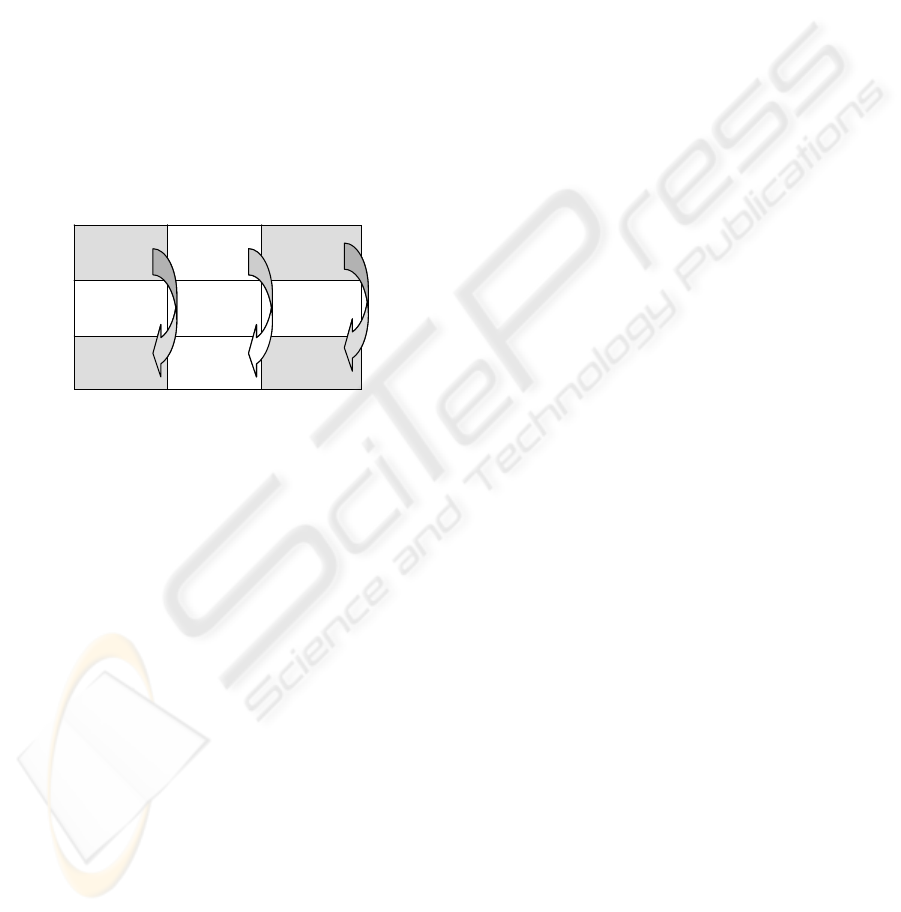
2 STRATEGIC GAMES MATRIX
The concepts, formulations and results from non-
cooperative dynamic game theory (Başar and
Olsder, 1999) open new possibilities as conceptual
platform for optimal strategy formulation.
In generic conflict of interests’ situations, the
description and mapping of a particular cooperative
or competitive confrontation between two or more
players can be accomplished with only two
dimensions: the ‘player posture assumption’ and the
‘player power-ratio assumption’. They are used to
build a (3x3) matrix called strategic games matrix
(SGM) (Costa and Bottura, 2006): The matrix
horizontal axis represents the player postures
assumptions: as rival, or individualistic, or
associative and, on the vertical axis represents the
player power-ratio assumptions: as hegemonic, or
balanced, or weak, as shown in Figure 1.
Figure 1: Typical strategic positions on the SGM
highlighting, in gray, the two hierarchical limit-case
strategic games.
These nine resulting strategic positions, at each
of the nine matrix’s cells, are named, respectively:
Dominant, Leader, Paternalistic, Retaliatory,
Competitive, Cooperative, Marginal, Follower, and
Solidary, which are words that represent each one of
the typical competitive confrontation strategic
positions players may explicitly or implicitly adopt
in a conflict of interests situation. In subsections 2.1
to 2.4 the five strategic positioning to which classic
equilibrium strategies apply - Minimax, Nash,
Pareto, for non-hierarchical games, and Stackelberg,
for hierarchical games - and the respective situations
where they normally occur, are described (Başar and
Olsder, 1999; Costa F
o
., 1992).
In subsections 2.5 and 2.6, the four special limit-
cases strategic positions, representing two
hierarchical games, not well covered by classic
equilibrium strategies from game theory, here called
Dominant-Marginal, and Paternalistic-Solidary, are
presented in the next Sections. (The formal concept
of dynamic games, of equilibrium point and of
equilibrium strategy here used can be found in
(Başar and Older, 1999)).
2.1 Retaliatory Games - Minimax
This strategic positioning applies to lose-win type
games - at the left-center SGM cell -, where the
players assume, explicit or implicitly, that a gain for
one implies in losses to the remainder,
characterizing a retaliatory game. For a zero-sum
game, a solution, if it exists, for which each player
acts towards what it understands as the most
favorable to optimize its own objective function,
considering all the possibilities the others could do,
is called a saddle-point. This point has the peculiar
characteristic that any deviation from it, by any of
the players, makes its result worsen in relation to its
objective function. For N players, a strategic
decision
Uu
ii
∈
ˆ
by each player P
i
is defined as a
saddle-point equilibrium solution if, for every
admissible set
1
{ ,..., ,..., }
iN
U
uuu
∈
, the following
relation is valid:
11 1
1
111
,..., , ,...,
111
,..., , ,...,
( ,..., , , ,..., )
( ,..., )
max
max
−+
−+
−+
≤
≤
iiN
i
N
i
ii N
uuu u
ii N
uuu u
i
û
Ju u u u
Ju u
.
This strategy applies also to real situations
where a player P
i
can imagine that another player
may have non-rational or erratic behavior, or even
malicious, i.e., that an adversary may make moves to
‘damage’ P
i
’s objectives.
2.2 Competitive Games - Nash
The strategic position at the center-center SGM cell,
named here as Competitive, describes situations of
‘perfect competition’, or ‘free market’, with many
suppliers, where none of them is capable of
dominating the remainders. In the non-cooperative
variable-sum games, where a player decides to play
a competitive strategic game, it seeks to optimize its
objective function ignoring what the other players
are doing or intending to do. If this solution exists, it
is characterized by the situation where none of the
players is able to improve its result by changing only
its own decision-control. Such set of decisions is the
Nash equilibrium point, defined below: A Nash
equilibrium point
1*
( ,..., ,..., )
iN
U
ûû û û
=
∈ ,
if it exists, for a non-cooperative game, with
K=1, and variable sum, with N players, is defined if,
for all
ii
uU
∈
,
iN
∈
,
it obeys simultaneously the N
following objective function inequalities:
Leader:
Stackelberg
game
Retaliatory:
Minimax
Cooperative:
Pareto
-
Player Power-ratio Assumptions
Player Postures Assumptions
Dominant
Solidary /
Marginal
Paternalistic
Nash
Follower:
Stackelberg
game
Rival Individualistic Associative
Weak
Ba l a n c e d
Hegemonic
Dominant
Solidary
Marginal
Paternalistic
Competitive:
Leader:
Stackelberg
game
Retaliatory:
Minimax
Cooperative:
Pareto
-
Player Power-ratio Assumptions
Player Postures Assumptions
Dominant
Solidary /
Marginal
Paternalistic
Nash
Follower:
Stackelberg
game
Rival Individualistic Associative
Weak
Ba l a n c e d
Hegemonic
Dominant
Solidary
Marginal
Paternalistic
Competitive:
THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS
HIERARCHICAL CONTROL STRATEGIES MODELING
185

11
11
( ,..., ,..., ) ( ,..., ,..., )
iN iN
ûûû uûû
JJ
≤
, ... ,
11
( ,..., ,..., ) ( ,..., ,..., )
iN iN
ii
ûûû ûuû
JJ
≤
, ... ,
11
( ,..., ,..., ) ( ,..., ,..., )
iN iN
NN
ûûû ûûu
JJ
≤
.
2.3 Cooperative Games – Pareto
For variable-sum games - at the right-center SGM
cell - the cooperation among players may lead to
results - for all of them - that are better than those
they would obtain if each one tries to optimize its
objective function without an a priori knowledge of
other’s decisions. When players decide to share
information on the respective constraints and
conditions, alternative actions and objective
functions, it is possible for them to find a point of
equilibrium, the ‘Pareto optimum’, which is ‘the
best’ possible for all players. This point, if it exists,
is characterized by the fact that none of the players
can improve its result without, with its action,
harming the other’s results. These are the so called
‘win-win games’. This type of game requires good
faith and loyalty among all participants.
For a
variable-sum cooperative game (
K=1) with N
players, the point
*1
( ,..., ,..., )
iN
ûû û û
U
=∈
is
defined as a Pareto optimum if there is no other
point
1
( ,..., ,..., )
iN
uuuu U
=∈
such that
() ()
ii
i
i
û
u
J
J
≤
,
N
i∀∈
.
This condition requires that
() ()
i
i
ii
û
J
uJ
≤
,
N
i∀∈
,
only if
() ()
i
i
ii
û
J
uJ
=
,
iN∀∈
, with a strict
inequality for at least one
i
N
∈
.
2.4 Leader-Follower Stackelberg
Games
The strategies applicable to hierarchical games with
a strongest player, the leader, and another weaker
player, the follower, are called Stackelberg
strategies and correspond to two opposed positions:
center-upper and center-lower SGM cells. Consider
a simplified hierarchical game between a player M,
called leader, and a player P, called follower, with
strategic decisions
λ
and
u
, and objective
functions
(,)Ru
λ
and
(,)
J
u
λ
, associated to players M
and P, respectively (Haimes and Li, 1988; Costa F
o
.
and Bottura, 1990, 1991). Let us suppose also that,
by the structure and rules of the game, player M
selects first its strategic decision
λ
and, then, player
P selects its strategic decision
u
, knowing
beforehand the M’s decision. The pair
(,) (, )uLU
λ
∈
,
if it exists, defines a Stackelberg
equilibrium point for which:
(a) There is a transformation
:
U
TL
→
such
that, for any given
L
λ
∈
,
(, ) (,)
JJu
T
λ
λλ
≤
for every
uU
∈
,
and (b) There is a
L
λ
∈
such that
),()
ˆ
,
ˆ
(
λλλλ
TRTR ≤
for every
L
λ
∈
, where
λ
ˆ
ˆ
Tu =
. Note that, to obtain a Stackelberg
equilibrium point, it is necessary that the follower be
a rational agent, always making optimal decisions
under its own game limitation. For this game
structure, one can determine a pair of Stackelberg
strategies - for the leader and for the follower -
typically applied to situations of conflict of interests
between a very strong player and another very weak,
both with individualistic concurrent assumptions.
2.5 Dominant-Marginal Games
The Dominant-Marginal games are played by two
players in two hierarchical antagonist strategic
positions, both with rival posture assumption:
(1) Dominant strategic position: A Dominant
strategic position - at the left-upper SGM cell -
characterizes the player which has all strength and
has the intention of destroying the smaller
competitors. Its attitude may be of intimidation,
blackmail, price war, for instance, to try to bankrupt
the small ones. It may pressure its clients not to
purchase from the small ones. A Dominant
equilibrium point limit-case for this game can be
obtained through the solution of a mono-criterion
stochastic optimization problem in which the player
in Dominant position ignores all the objective
functions of its ‘small’ opponents and simply
optimizes its own objective function. The player at a
Dominant position could treat the possible actions of
‘small’ competitors simply as random noises.
(2) Marginal strategic position: Countering the
Dominant position as described above, is the
marginal strategic position - at the left-lower SGM
cell -, where a weaker however courageous and
competitive player in the game does everything it
understands as necessary to survive, trying, as much
as possible, to obtain some advantages upon causing
losses to the major game dominator. A marginal
equilibrium point limit-case for this game can be
obtained through the solution of an optimization
problem in which the Marginal position player, for
instance, instead of minimizing, tries to maximize
the
main and stronger competitor’s objective function
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
186

with the purpose of infringing upon it the maximum
possible damage.
2.6 Paternalistic-Solidary Games
This game is played also by two players in two
hierarchical antagonist strategic positions, both with
associative posture assumption:
(1) Paternalistic strategic position: The
paternalistic strategic position - at the upper-right
SGM cell - occurs in games where a more powerful
player, by its own decision, shapes its own actions
and those of the remaining weaker players in the
game, seeking preservation and development of the
system as a whole. It is a game similar to the
situation of a family father, supposed to have
complete authority over the small children: he does
all he comprehends to be necessary to promote the
development, growth and harmony within his
family, in a paternalistic way. A paternalistic
equilibrium point limit-case game can be found as
follows: Let 0
i
α
≤≤
1
be a relative importance
weight for the player P
i
such that
1
N
i
i
α
=
∑
= 1, and let
1
(...)
N
i
ii
z
J
α
=
∑
=
be a multi-criteria objective
function, encompassing all the objective functions of
all the N players, the new function to be optimized.
A paternalistic equilibrium point for this limit-case
game can be found as a solution to a multi-criteria
optimization problem (Bryson and Ho, 1975) where
the new objective function is a linear combination of
all the objective functions for all players. Otherwise,
the Paternalistic player should take in account, on
its decision, the ‘risk’ of a Solidary player decision
for an alternative solitary strategy, leaving the game.
(2) Solidary strategic position: In opposition to
the paternalistic position described above is the
Solidary position - at the right-lower SGM cell -,
that represents the situation of a player, in a game, in
a weaker, however associative position which,
without the power to impose its interests upon the
others, seeks to follow the rules established by the
‘ruling power’, looking for some individual
advantage. Otherwise it prefers to leave the game.
This is how a member behaves in relation to its
cooperative organization: it simply needs to decide
whether it should join the ‘collective’ and obtain
some advantage or, alternatively, it should rather act
on its own. A solidary equilibrium solution for this
limit-case game can be treated as a simple decision
tree problem with only two branches, representing
the alternative decisions: ‘join the collective’, or
‘work alone’.
3 HIERARCHICAL GAMES
Departing from classic concepts and formulations
from dynamic game theory, a formal conceptual
platform for multilevel multiple decision-control
problem formulation is built. A deterministic
dynamic game (DDG) with several participants and
multiple stages can be modeled as a systems
optimization problem with multiple decentralized
and autonomous decision-makers, called the
‘players’ –or intelligent autonomous agents. From
the point of view of systems control theory, a DDG
is associated with a particular problem of optimal
control with multiple intelligent autonomous
controllers, or agents (Bryson and Ho, 1975).
In this type of games, each one of the N agents -
or players - receiving information progressively
disclosed by the structure of the game and
considering the possible decisions of other agents,
makes a sequence of decisions, stage by stage,
attempting to optimize one’s objective function
-
while obeying the game constraints. For a formal
presentation of the optimization problem introduced
above, let us adopt the notation derived from the
terminology of systems theory (Başar and Olsder,
1999). Hierarchical architectures games with two
levels, designed by HG2, and with three levels,
designed by HG3, for multiple intelligent
autonomous agents control strategies, are here
described. A two-level hierarchical game, HG2, can
be modeled through a similar process of forming a
group of subsystems, each one representing a
competing agent – for instance, a company. Each
company - the i
th
- here represented by a subsystem
CS
i
, vies in the market for raw materials, specialized
production manpower, managerial resources,
financial resources, technology, and other supplies.
On the other hand, it also competes in the market for
clients’ preferences. The market, in the broader
sense, also interferes in the game, acting upon prices
and quantities transacted by the N agents with their
clients and providers. The formulation of this
concept can be obtained through a convenient
partition and segmentation process of the DDG
game: The HG2 is formed by two types of
subsystems: the Companies Subsystems, CS
i
, and
the Market Coordinator Subsystems, MCS. The CS
i
modules communicate with the market coordinator
subsystem, MCS, which informs to each one of
them, at the beginning of each new period, its
decision parameter. The CS
i
, in turn, informs the
MCS about their coordinated decisions
for the next
period. The dynamic hierarchical game HG-2 can be
similarly expanded applying to each subsystem CS
i
a segmentation process, where each i
th
competing
THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS
HIERARCHICAL CONTROL STRATEGIES MODELING
187
agent is assumed to consist of G Managerial Units,
MU
ij
, where
{1, 2,..., }jG∈
, introducing G new
intelligent autonomous agents for each company.
These managerial units, MU
ij
,
represent the main
functional or managerial areas of the company. In
this sense, each MU
ij
, as any intelligent autonomous
agent, has its own state transition equation,
information structure, strategy, decision, and
specific objective function to be optimized.
Therefore, the segmentation described produces a
three-level hierarchical game HG-3 wherein the
coordination, at the second level, is achieved by a
new module called CSC
i
, representing the
coordination of all the MU
ij
, by the i
th
company’s
chief executive.
4 SGM APPLICATIONS
Let us apply, now, with illustrative purposes, the
SGM methodology for a complex structure analysis
to some HG-3 structured games.
4.1 Structure with One Coordinator
Suppose a complex business-economic structured
system, with three decision hierarchical levels.
Proceeding accord to this methodology the
following results can be obtained:
(A) The four sub-games identified are:
{CS
1
,…,CS
i
,…,CS
N
} competing - or cooperating -
sub-game; {MU
i1
,…, MU
ij
, MU
iG
} competing - or
cooperating - subgame; {MCS, CS
i
} hierarchical
coordination sub-game; {CSC
i
, MU
ij
} hierarchical
coordination sub-game.
(B) The application of one or another
equilibrium strategy on each specific sub-game
depends on each particular situation of conflict of
interests and on the postures and assumptions
present in each case:
(i) The competitive sub-game among CS
i
companies could be treated as a game where the
agents are supposed to work in a variable-sum
objective function environment, acting
independently from each other and prevented from
sharing information and from cooperating with each
other. They are forbidden to make coordinated
decisions to optimize together their objective
functions; consequently, for this sub-game, the Nash
equilibrium strategy is the applicable, as in
subsection 2.2.
(ii) Among those responsible for the MU
ij
Managerial Units on the same company, a sub-game
is played where the agents aim to optimize a
variable-sum objective function for which
cooperation among the unit managers in charge is
expected; hence, for this sub-game, the Pareto
equilibrium strategy is the applicable, as in
subsection 2.3.
(iii) The relationship between the agent MCS,
the market coordinator, representing the market
action, and each CS
i
company
could be interpreted
as a sub-game with hierarchical coordination among
them; therefore, the Stackelberg equilibrium
strategies pair is applicable, considering the market
coordinator as the Leader and each CS
i
as a
Follower, as in subsection 2.4;
(iv) The relationship between the agent CSC
i
,
internal coordinator of each company, and each MU
ij
could be considered as a hierarchical coordination
sub-game; so, the Stackelberg equilibrium strategy
pair is applicable, considering the coordinator CSCi
as the Leader and each MUij as a Follower, as in
subsection 2.4.
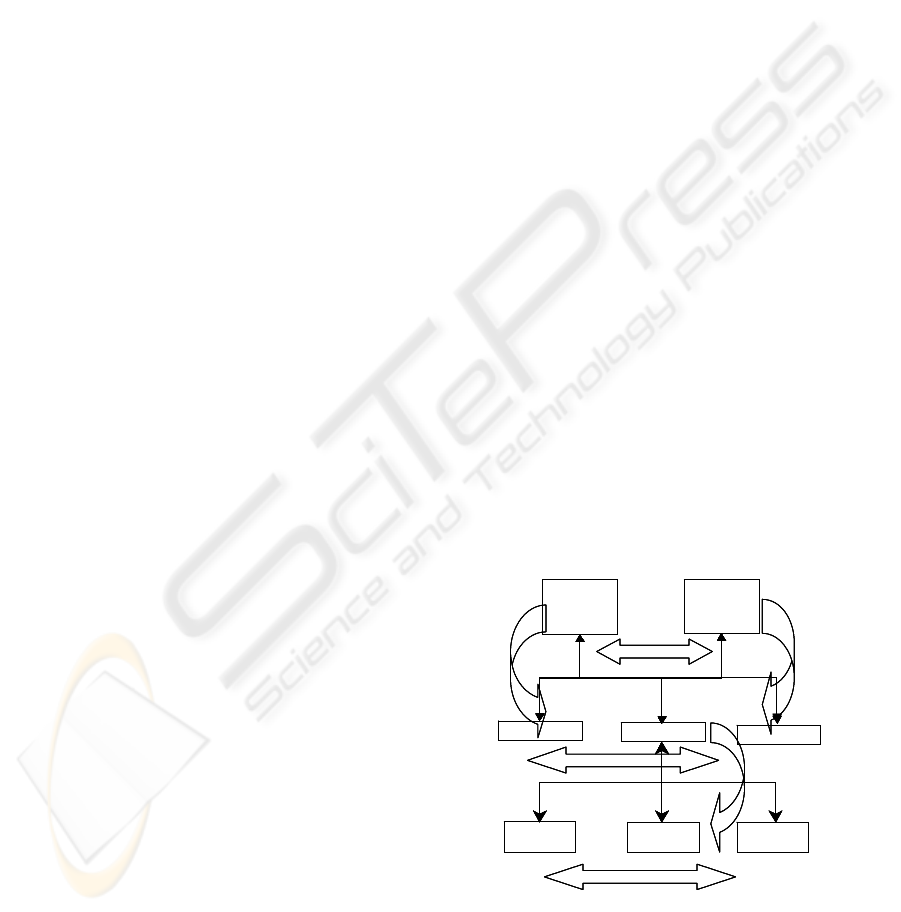
(C) The structured mapping resulting from the
fourth stage, easy to obtain in this case, is also
indicated in Figure 2. Classic ways of solving these
types of optimal control problems could use, for
instance, Pontryagin’s Minimum Principle, or
Calculus of Variations, or Dynamic Programming
(Bryson and Ho, 1975), depending on the case.
4.2 Structure with Two Coordinators
This subsection presents, in a summarized form,
another illustrative application of this methodology
for analysis of another type of hierarchic structure.
Let us take the former HG-3 as a basis and introduce
a second coordinator agent at the first level, as
shown in Figure 2.
Figure 2: Game equilibrium strategies applied to a three-
level multiple decision control architecture with two
coordinators.
This structure has now two market coordinators,
one representing the market coordinator –supplier–,
Company-Player 1
Market
Coordinator
Supplier
Player
. . .
. . .
3
rd
Level
1
st
Level
Retaliatory sub -game
Pareto sub -game
Market
Coordinator
Consumer
Player
Nash sub -game
Dominant –
Marginal
sub -game
MU
ij
MCSS
MCSC
CSC
i
. . .
. . .
. . .
Manager-Unit
Player i,1
. . .
3
rd
Level
2
nd
Level2
nd
Level
1
st
Level
Retaliatory sub -game
Pareto sub -game
Paternalistic -
Solidary/Solitary
sub -game
Paternalistic -
Solidary/Solitary
sub -game
Stackelberg:
Leader -Follower
sub -game
Stackelberg:
Leader -Follower
sub -game
Nash sub -game
Dominant –
Marginal
sub -game
MU
ij
CS
i
CS
i
MCSS
MCSC
CSC
i
. . .
. . .
Company-Player i
Company-Player N
Manager-Unit
Player i,j
Player i,G
Manager-Unit
Company-Player 1Company-Player 1
Market
Coordinator
Supplier
Player
. . .
. . .
3
rd
Level
1
st
Level
Retaliatory sub -game
Pareto sub -game
Market
Coordinator
Consumer
Player
Market
Coordinator
Consumer
Player
Nash sub -game
Dominant –
Marginal
sub -game
MU
ij
MCSS
MCSC
CSC
i
. . .
. . .
. . .
Manager-Unit
Player i,1
. . .
3
rd
Level
2
nd
Level2
nd
Level2
nd
Level2
nd
Level
1
st
Level
Retaliatory sub -game
Pareto sub -game
Paternalistic -
Solidary/Solitary
sub -game
Paternalistic -
Solidary/Solitary
sub -game
Paternalistic -
Solidary/Solitary
sub -game
Paternalistic -
Solidary/Solitary
sub -game
Stackelberg:
Leader -Follower
sub -game
Stackelberg:
Leader -Follower
sub -game
Stackelberg:
Leader -Follower
sub -game
Stackelberg:
Leader -Follower
sub -game
Nash sub -game
Dominant –
Marginal
sub -game
MU
ij
CS
i
CS
i
CS
i
CS
i
MCSS
MCSC
CSC
i
. . .
. . .
Company-Player iCompany-Player i
Company-Player NCompany-Player N
Manager-Unit
Player i,j
Player i,G
Manager-Unit
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
188

MCSS, and another market coordinator –consumer–
, MCSC. The resulting structural mapping obtained
from a similar use of the four stages methodology,
and the corresponding equilibrium strategies
applicable to each sub-game identified, are shown in
Figure 2.
5 FINAL CONCLUSIONS
In this paper the strategic games matrix (SGM)
modeling framework is used as a tool for:
• Describing, characterizing, and mapping a wide
variety of conflicts of interests situations among
intelligent autonomous agents, both for hierarchical
and for non-hierarchical games, in an integrated
manner;
• Modeling, analysis and design of multilevel
multiple-agent control architectures in an integrated
manner, making explicit the obvious conflicts of
interests possibilities;
• Establishing a useful two-way conceptual bridge
between game theory and multiple-agent structures
analysis and design.
The SGM permits to evidence that, for a specific
real complex problem, we should be more concerned
with the choice of the right game to model,
than with
the right way to solve the game
, in spite of the
importance of these techniques.
REFERENCES
Alpcan, T., Başar, T., 2002. “A game-theoretic
framework for congestion control in general topology
networks”, Proc. 41st IEEE CDC, Las Vegas, Nevada.
Alpcan, T., Başar, T., 2004. “A game theoretic analysis of
intrusion detection in access control systems”, Proc.
43
rd
IEEE CDC, Atlantis, Paradise Islands, Bahamas.
Başar, T., Olsder, G. J., 1999. Dynamic non-cooperative
game theory. Philadelphia, PA: SIAM, Series in
Classics in Applied Mathematics, 1999.
Bohacek, S., Hespanha, J. P., Obraczka, K., 2002. “Saddle
policies for secure routing in communication
networks”, Proc. 41
st
IEEE CDC, Las Vegas, Nevada.
Bottura C. P., Costa, E. A., 2004, “Business strategy
formulation modeling via hierarchical dynamic game”,
Proc. CSIMTA International Conference, Cherbourgh,
France.
Brandenburger, A. M., Nalebuff, B. J., 1995. “The right
game: Use of game theory to shape strategy”, Harvard
Business Review, pp.57-81.
Bryson Jr., A. E, Ho, Y. C., 1975. Applied optimal control.
Washington, DC: Hemisphere.
Castañón, D. A., Pachter, M., Chandler, P. R., 2004. “A
game of deception”, Proc. 43
rd
IEEE, CDC, Atlantis,
Paradise Islands, Bahamas.
Costa Fº, J. T., Bottura, C. P., 1990. “Parallel optimal
hierarchical control using a MIMD architecture”,
Proc. 29
th
IEEE CDC, Honolulu.
Costa Fº, J. T., Bottura, C. P., 1991. “Hierarchical
multidecision making on a computer network with
distributed coordination and control”, Proc. 39
th
Annual Allerton Conference on Communication
Control and Computing, Urbana, IL, pp. 703-704.
Costa Fº., J. T., 1992. “Proposta para computação
assíncrona paralela e distribuída de estruturas especiais
de jogos dinâmicos”, Universidade Estadual de
Campinas, Faculdade de Engenharia Elétrica, Tese de
Doutorado, Campinas, SP, Brazil.
Costa, E. A., Bottura, C. P., 2006. “The Strategic Games
Matrix (SGM) as a new tool for strategic management
via game theory”, Sistemas & Gestão, 1 (1) pp. 17-41.
(in
http://www.latec.com.br/sg/arevista/Volume1/Numero
1/V1_1_index.htm ).
Cruz Jr., J. B., 1978. “Leader-follower strategies for
multilevel systems”, IEEE Trans. on Automatic
Control,
vol. AC-23 (2), pp. 244-255.
Dimarogonas, D. V., Kyriakopoulus, K. J., 2005. “A
feedback stabilization and collision avoidance scheme
for multiple independent nonholonomic non-point
agents”, Proc. 2005 IEEE Int. Symposium on
Intelligent Control, Limassol, Cyprus.
Haimes, Y. Y., Li, D., 1988. “Hierarchical multiobjective
analysis for large-scale systems: Review and current
status”, Automatica, vol. 24 (1), pp. 53-69.
Liu, Y., Galati, D. G., Simaan, M. A., 2004, “A game
theoretic approach to team dynamics and tactics in
mixed initiative control of automa-teams”, Proc. 43
rd
IEEE CDC, Atlantis, Paradise Islands, Bahamas.
Rahimi-Kian, A. Tabarraei, H., Sadeghi, B., 2005.
“Reinforcement learning based supplier-agents for
electricity markets”, Proc. 2005 IEEE Int. Symposium
on Intelligent Control, Limassol, Cyprus.
Schelling, T. C., 1960. The strategy of conflict. New York,
NY: Harvard University Press.
Shao, J., Xie, G., Yu, J., Wang, L., 2005. “Leader-
following formation control of multiple mobile
robots”, Proc. 2005 IEEE Int. Symposium on
Intelligent Control, Limassol, Cyprus.
Shi, H., Wang, L., T. Chu, T., 2005. “Coordination of
multiple dynamic agents with asymmetric
interactions”, Proc. 2005 IEEE Int. Symposium on
Intelligent Control, Limassol, Cyprus.
THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS
HIERARCHICAL CONTROL STRATEGIES MODELING
189
