THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR

INTELLIGENT AUTONOMOUS AGENTS HIERARCHICAL

CONTROL STRATEGIES MODELING

Eliezer Arantes da Costa and Celso Pascoli Bottura

LCSI – FEEC - UNICAMP – Cidade Universitária Zeferino Vaz, Campinas, SP, Brazil

Keywords: Autonomous agents, competitive games, cooperative games, distributed intelligent control, hierarchical

architectures, hierarchical control, multiple agent control, Strategic Games Matrix, strategies modeling.

Abstracts: This paper presents a framework for strategy formulation in multilevel multiple-agent control system

architectures based on the Strategic Games Matrix (SGM), having game theory and control systems theory

as basic concepts and models. New methodologies for analysis and for design of hierarchical control

architectures with multiple intelligent autonomous agents, based on the SGM concept, are applied.

Illustrative hierarchical control applications to system architectures analysis and synthesis based on the

SGM are presented.

1 INTRODUCTION

The study of hierarchical multi-agent control

systems is receiving growing attention within the

control community. Driving applications of multiple

agents control include: mobile robots coordination

and control, satellite clusters, automated highways,

unmanned aerial vehicles (UAV), distributed

artificial intelligence, and strategic planning in

general.

A wide diversity of multi-controller and

coordination problems has been treated recently,

e.g., multiple mobile agents moving coordination

and control (Shi, Wang and Chu, 2005), traffic

congestion control (Alpcan and Başar, 2002),

multiple mobile robot control (Shao, Xie, Yu and

Wang, 2005), collision avoidance scheme in

navigation control (Dimaragonas and

Kyriakopoulus, 2005), secure routing in

communication networks (Bohacek, Hespanha and

Obraczka, 2002), optimal bidding strategies in the

electricity market (Rahimi-Kian, Tabarraei and

Sadeghi, 2005), automa-teams coordination and

control (Liu, Galati and Simaan, 2004), attack and

deception strategies in military operations

(Castañón, Pachter and Chandler, 2004), and

intrusion detection in access control systems

(Alpcan and Başar, 2004).

Mathematical approaches used in these papers

treat the control problems as Nash, Pareto,

Stackelberg, Minimax games, or some variations of

them, in an insulated manner.

The formulation of optimal strategies in

competitive and/or cooperative environments has

constituted one of the main challenges for

researchers and scholars (Schelling, 1960;

Brandenburger and Nalebuff, 1995; and Bottura and

Costa, 2004) and a wide variety of approaches has

been proposed and used (Başar and Older, 1999;

Costa F

., 1992; and Cruz Jr., 1978). However, a

structured combination of all these possible

approaches on the same hierarchical architecture

should be conceived, formulated, and should have its

usefulness exhibited. Here, an integrated framework

considering these classical games on the same

analytical structure, by going a step further on the

traditional approach used in papers like the above

mentioned, is presented.

In this paper, an ‘agent’ represents a controller, a

decision-maker, a commander, an autonomous

robot, a player – person or team –, software, a

policy-maker, a UAV, a stakeholder, or any human

being. Our approach treats hierarchical, non-

hierarchical, or heterarchical architectures as a

structured collections of sub-games.

184

Arantes da Costa E. and Pascoli Bottura C. (2007).

THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS HIERARCHICAL CONTROL STRATEGIES

MODELING.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 184-189

DOI: 10.5220/0001625001840189

 SciTePress

2 STRATEGIC GAMES MATRIX

The concepts, formulations and results from non-

cooperative dynamic game theory (Başar and

Olsder, 1999) open new possibilities as conceptual

platform for optimal strategy formulation.

In generic conflict of interests’ situations, the

description and mapping of a particular cooperative

or competitive confrontation between two or more

players can be accomplished with only two

dimensions: the ‘player posture assumption’ and the

‘player power-ratio assumption’. They are used to

build a (3x3) matrix called strategic games matrix

(SGM) (Costa and Bottura, 2006): The matrix

horizontal axis represents the player postures

assumptions: as rival, or individualistic, or

associative and, on the vertical axis represents the

player power-ratio assumptions: as hegemonic, or

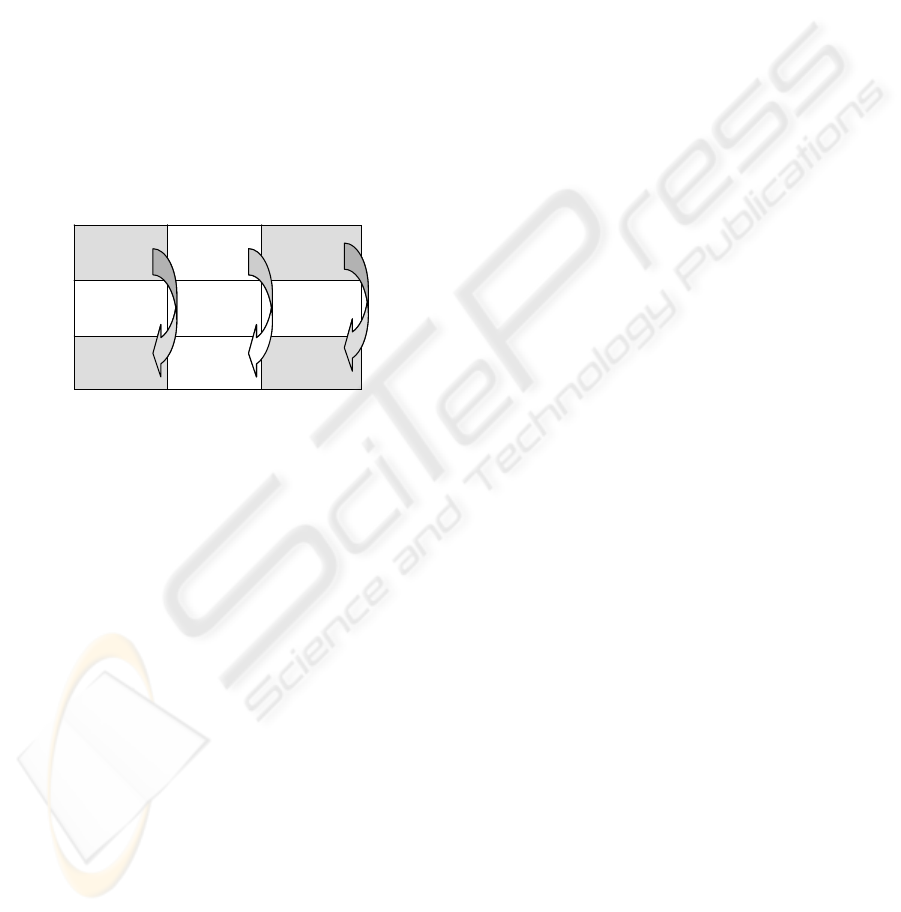
balanced, or weak, as shown in Figure 1.

Figure 1: Typical strategic positions on the SGM

highlighting, in gray, the two hierarchical limit-case

strategic games.

These nine resulting strategic positions, at each

of the nine matrix’s cells, are named, respectively:

Dominant, Leader, Paternalistic, Retaliatory,

Competitive, Cooperative, Marginal, Follower, and

Solidary, which are words that represent each one of

the typical competitive confrontation strategic

positions players may explicitly or implicitly adopt

in a conflict of interests situation. In subsections 2.1

to 2.4 the five strategic positioning to which classic

equilibrium strategies apply - Minimax, Nash,

Pareto, for non-hierarchical games, and Stackelberg,

for hierarchical games - and the respective situations

where they normally occur, are described (Başar and

Olsder, 1999; Costa F

., 1992).

In subsections 2.5 and 2.6, the four special limit-

cases strategic positions, representing two

hierarchical games, not well covered by classic

equilibrium strategies from game theory, here called

Dominant-Marginal, and Paternalistic-Solidary, are

presented in the next Sections. (The formal concept

of dynamic games, of equilibrium point and of

equilibrium strategy here used can be found in

(Başar and Older, 1999)).

2.1 Retaliatory Games - Minimax

This strategic positioning applies to lose-win type

games - at the left-center SGM cell -, where the

players assume, explicit or implicitly, that a gain for

one implies in losses to the remainder,

characterizing a retaliatory game. For a zero-sum

game, a solution, if it exists, for which each player

acts towards what it understands as the most

favorable to optimize its own objective function,

considering all the possibilities the others could do,

is called a saddle-point. This point has the peculiar

characteristic that any deviation from it, by any of

the players, makes its result worsen in relation to its

objective function. For N players, a strategic

decision

∈

by each player P

is defined as a

saddle-point equilibrium solution if, for every

admissible set

{ ,..., ,..., }

uuu

∈

, the following

relation is valid:

11 1

111

,..., , ,...,

111

,..., , ,...,

( ,..., , , ,..., )

( ,..., )

max

−+

≤

iiN

ii N

uuu u

ii N

uuu u

Ju u u u

Ju u

This strategy applies also to real situations

where a player P

can imagine that another player

may have non-rational or erratic behavior, or even

malicious, i.e., that an adversary may make moves to

‘damage’ P

’s objectives.

2.2 Competitive Games - Nash

The strategic position at the center-center SGM cell,

named here as Competitive, describes situations of

‘perfect competition’, or ‘free market’, with many

suppliers, where none of them is capable of

dominating the remainders. In the non-cooperative

variable-sum games, where a player decides to play

a competitive strategic game, it seeks to optimize its

objective function ignoring what the other players

are doing or intending to do. If this solution exists, it

is characterized by the situation where none of the

players is able to improve its result by changing only

its own decision-control. Such set of decisions is the

Nash equilibrium point, defined below: A Nash

equilibrium point

( ,..., ,..., )

ûû û û

∈ ,

if it exists, for a non-cooperative game, with

K=1, and variable sum, with N players, is defined if,

for all

∈

it obeys simultaneously the N

following objective function inequalities:

Leader:

Stackelberg

game

Retaliatory:

Minimax

Cooperative:

Pareto

Player Power-ratio Assumptions

Player Postures Assumptions

Dominant

Solidary /

Marginal

Paternalistic

Nash

Follower:

Stackelberg

game

Rival Individualistic Associative

Weak

Ba l a n c e d

Hegemonic

Dominant

Solidary

Marginal

Paternalistic

Competitive:

Leader:

Stackelberg

game

Retaliatory:

Minimax

Cooperative:

Pareto

Player Power-ratio Assumptions

Player Postures Assumptions

Dominant

Solidary /

Marginal

Paternalistic

Nash

Follower:

Stackelberg

game

Rival Individualistic Associative

Weak

Ba l a n c e d

Hegemonic

Dominant

Solidary

Marginal

Paternalistic

Competitive:

THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS

HIERARCHICAL CONTROL STRATEGIES MODELING

185

( ,..., ,..., ) ( ,..., ,..., )

iN iN

ûûû uûû

≤

, ... ,

( ,..., ,..., ) ( ,..., ,..., )

iN iN

ûûû ûuû

≤

, ... ,

( ,..., ,..., ) ( ,..., ,..., )

iN iN

ûûû ûûu

≤

2.3 Cooperative Games – Pareto

For variable-sum games - at the right-center SGM

cell - the cooperation among players may lead to

results - for all of them - that are better than those

they would obtain if each one tries to optimize its

objective function without an a priori knowledge of

other’s decisions. When players decide to share

information on the respective constraints and

conditions, alternative actions and objective

functions, it is possible for them to find a point of

equilibrium, the ‘Pareto optimum’, which is ‘the

best’ possible for all players. This point, if it exists,

is characterized by the fact that none of the players

can improve its result without, with its action,

harming the other’s results. These are the so called

‘win-win games’. This type of game requires good

faith and loyalty among all participants.

For a

variable-sum cooperative game (

K=1) with N

players, the point

( ,..., ,..., )

ûû û û

=∈

defined as a Pareto optimum if there is no other

point

( ,..., ,..., )

uuuu U

=∈

such that

() ()

≤

i∀∈

This condition requires that

() ()

≤

i∀∈

only if

() ()

iN∀∈

, with a strict

inequality for at least one

∈

2.4 Leader-Follower Stackelberg

Games

The strategies applicable to hierarchical games with

a strongest player, the leader, and another weaker

player, the follower, are called Stackelberg

strategies and correspond to two opposed positions:

center-upper and center-lower SGM cells. Consider

a simplified hierarchical game between a player M,

called leader, and a player P, called follower, with

strategic decisions

and

, and objective

functions

(,)Ru

and

(,)

, associated to players M

and P, respectively (Haimes and Li, 1988; Costa F

and Bottura, 1990, 1991). Let us suppose also that,

by the structure and rules of the game, player M

selects first its strategic decision

and, then, player

P selects its strategic decision

, knowing

beforehand the M’s decision. The pair



(,) (, )uLU

∈

if it exists, defines a Stackelberg

equilibrium point for which:

(a) There is a transformation

→

such

that, for any given

∈

(, ) (,)

JJu

λλ

≤

for every

∈

and (b) There is a



∈

such that

),()

(

λλλλ

TRTR ≤

for every

∈

, where

Tu =

. Note that, to obtain a Stackelberg

equilibrium point, it is necessary that the follower be

a rational agent, always making optimal decisions

under its own game limitation. For this game

structure, one can determine a pair of Stackelberg

strategies - for the leader and for the follower -

typically applied to situations of conflict of interests

between a very strong player and another very weak,

both with individualistic concurrent assumptions.

2.5 Dominant-Marginal Games

The Dominant-Marginal games are played by two

players in two hierarchical antagonist strategic

positions, both with rival posture assumption:

(1) Dominant strategic position: A Dominant

strategic position - at the left-upper SGM cell -

characterizes the player which has all strength and

has the intention of destroying the smaller

competitors. Its attitude may be of intimidation,

blackmail, price war, for instance, to try to bankrupt

the small ones. It may pressure its clients not to

purchase from the small ones. A Dominant

equilibrium point limit-case for this game can be

obtained through the solution of a mono-criterion

stochastic optimization problem in which the player

in Dominant position ignores all the objective

functions of its ‘small’ opponents and simply

optimizes its own objective function. The player at a

Dominant position could treat the possible actions of

‘small’ competitors simply as random noises.

(2) Marginal strategic position: Countering the

Dominant position as described above, is the

marginal strategic position - at the left-lower SGM

cell -, where a weaker however courageous and

competitive player in the game does everything it

understands as necessary to survive, trying, as much

as possible, to obtain some advantages upon causing

losses to the major game dominator. A marginal

equilibrium point limit-case for this game can be

obtained through the solution of an optimization

problem in which the Marginal position player, for

instance, instead of minimizing, tries to maximize

the

main and stronger competitor’s objective function

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

186

with the purpose of infringing upon it the maximum

possible damage.

2.6 Paternalistic-Solidary Games

This game is played also by two players in two

hierarchical antagonist strategic positions, both with

associative posture assumption:

(1) Paternalistic strategic position: The

paternalistic strategic position - at the upper-right

SGM cell - occurs in games where a more powerful

player, by its own decision, shapes its own actions

and those of the remaining weaker players in the

game, seeking preservation and development of the

system as a whole. It is a game similar to the

situation of a family father, supposed to have

complete authority over the small children: he does

all he comprehends to be necessary to promote the

development, growth and harmony within his

family, in a paternalistic way. A paternalistic

equilibrium point limit-case game can be found as

follows: Let 0

≤≤

be a relative importance

weight for the player P

such that

∑

= 1, and let

(...)

∑

be a multi-criteria objective

function, encompassing all the objective functions of

all the N players, the new function to be optimized.

A paternalistic equilibrium point for this limit-case

game can be found as a solution to a multi-criteria

optimization problem (Bryson and Ho, 1975) where

the new objective function is a linear combination of

all the objective functions for all players. Otherwise,

the Paternalistic player should take in account, on

its decision, the ‘risk’ of a Solidary player decision

for an alternative solitary strategy, leaving the game.

(2) Solidary strategic position: In opposition to

the paternalistic position described above is the

Solidary position - at the right-lower SGM cell -,

that represents the situation of a player, in a game, in

a weaker, however associative position which,

without the power to impose its interests upon the

others, seeks to follow the rules established by the

‘ruling power’, looking for some individual

advantage. Otherwise it prefers to leave the game.

This is how a member behaves in relation to its

cooperative organization: it simply needs to decide

whether it should join the ‘collective’ and obtain

some advantage or, alternatively, it should rather act

on its own. A solidary equilibrium solution for this

limit-case game can be treated as a simple decision

tree problem with only two branches, representing

the alternative decisions: ‘join the collective’, or

‘work alone’.

3 HIERARCHICAL GAMES

Departing from classic concepts and formulations

from dynamic game theory, a formal conceptual

platform for multilevel multiple decision-control

problem formulation is built. A deterministic

dynamic game (DDG) with several participants and

multiple stages can be modeled as a systems

optimization problem with multiple decentralized

and autonomous decision-makers, called the

‘players’ –or intelligent autonomous agents. From

the point of view of systems control theory, a DDG

is associated with a particular problem of optimal

control with multiple intelligent autonomous

controllers, or agents (Bryson and Ho, 1975).

In this type of games, each one of the N agents -

or players - receiving information progressively

disclosed by the structure of the game and

considering the possible decisions of other agents,

makes a sequence of decisions, stage by stage,

attempting to optimize one’s objective function

while obeying the game constraints. For a formal

presentation of the optimization problem introduced

above, let us adopt the notation derived from the

terminology of systems theory (Başar and Olsder,

1999). Hierarchical architectures games with two

levels, designed by HG2, and with three levels,

autonomous agents control strategies, are here

described. A two-level hierarchical game, HG2, can

be modeled through a similar process of forming a

group of subsystems, each one representing a

competing agent – for instance, a company. Each

company - the i

- here represented by a subsystem

, vies in the market for raw materials, specialized

production manpower, managerial resources,

financial resources, technology, and other supplies.

On the other hand, it also competes in the market for

clients’ preferences. The market, in the broader

sense, also interferes in the game, acting upon prices

and quantities transacted by the N agents with their

clients and providers. The formulation of this

concept can be obtained through a convenient

partition and segmentation process of the DDG

game: The HG2 is formed by two types of

subsystems: the Companies Subsystems, CS

, and

the Market Coordinator Subsystems, MCS. The CS

modules communicate with the market coordinator

subsystem, MCS, which informs to each one of

them, at the beginning of each new period, its

decision parameter. The CS

, in turn, informs the

MCS about their coordinated decisions

for the next

period. The dynamic hierarchical game HG-2 can be

similarly expanded applying to each subsystem CS

a segmentation process, where each i

competing

THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS

HIERARCHICAL CONTROL STRATEGIES MODELING

187

agent is assumed to consist of G Managerial Units,

, where

{1, 2,..., }jG∈

, introducing G new

intelligent autonomous agents for each company.

These managerial units, MU

represent the main

functional or managerial areas of the company. In

this sense, each MU

, as any intelligent autonomous

agent, has its own state transition equation,

information structure, strategy, decision, and

specific objective function to be optimized.

Therefore, the segmentation described produces a

three-level hierarchical game HG-3 wherein the

coordination, at the second level, is achieved by a

new module called CSC

, representing the

coordination of all the MU

, by the i

company’s

chief executive.

4 SGM APPLICATIONS

Let us apply, now, with illustrative purposes, the

SGM methodology for a complex structure analysis

to some HG-3 structured games.

4.1 Structure with One Coordinator

Suppose a complex business-economic structured

system, with three decision hierarchical levels.

Proceeding accord to this methodology the

following results can be obtained:

(A) The four sub-games identified are:

{CS

,…,CS

} competing - or cooperating -

sub-game; {MU

,…, MU

, MU

} competing - or

cooperating - subgame; {MCS, CS

} hierarchical

coordination sub-game; {CSC

, MU

} hierarchical

coordination sub-game.

(B) The application of one or another

equilibrium strategy on each specific sub-game

depends on each particular situation of conflict of

interests and on the postures and assumptions

present in each case:

(i) The competitive sub-game among CS

companies could be treated as a game where the

agents are supposed to work in a variable-sum

objective function environment, acting

independently from each other and prevented from

sharing information and from cooperating with each

other. They are forbidden to make coordinated

decisions to optimize together their objective

functions; consequently, for this sub-game, the Nash

equilibrium strategy is the applicable, as in

subsection 2.2.

(ii) Among those responsible for the MU

Managerial Units on the same company, a sub-game

is played where the agents aim to optimize a

variable-sum objective function for which

cooperation among the unit managers in charge is

expected; hence, for this sub-game, the Pareto

equilibrium strategy is the applicable, as in

subsection 2.3.

(iii) The relationship between the agent MCS,

the market coordinator, representing the market

action, and each CS

company

could be interpreted

as a sub-game with hierarchical coordination among

them; therefore, the Stackelberg equilibrium

strategies pair is applicable, considering the market

coordinator as the Leader and each CS

as a

Follower, as in subsection 2.4;

(iv) The relationship between the agent CSC

internal coordinator of each company, and each MU

could be considered as a hierarchical coordination

sub-game; so, the Stackelberg equilibrium strategy

pair is applicable, considering the coordinator CSCi

as the Leader and each MUij as a Follower, as in

subsection 2.4.

fourth stage, easy to obtain in this case, is also

indicated in Figure 2. Classic ways of solving these

types of optimal control problems could use, for

instance, Pontryagin’s Minimum Principle, or

Calculus of Variations, or Dynamic Programming

(Bryson and Ho, 1975), depending on the case.

4.2 Structure with Two Coordinators

This subsection presents, in a summarized form,

another illustrative application of this methodology

for analysis of another type of hierarchic structure.

Let us take the former HG-3 as a basis and introduce

a second coordinator agent at the first level, as

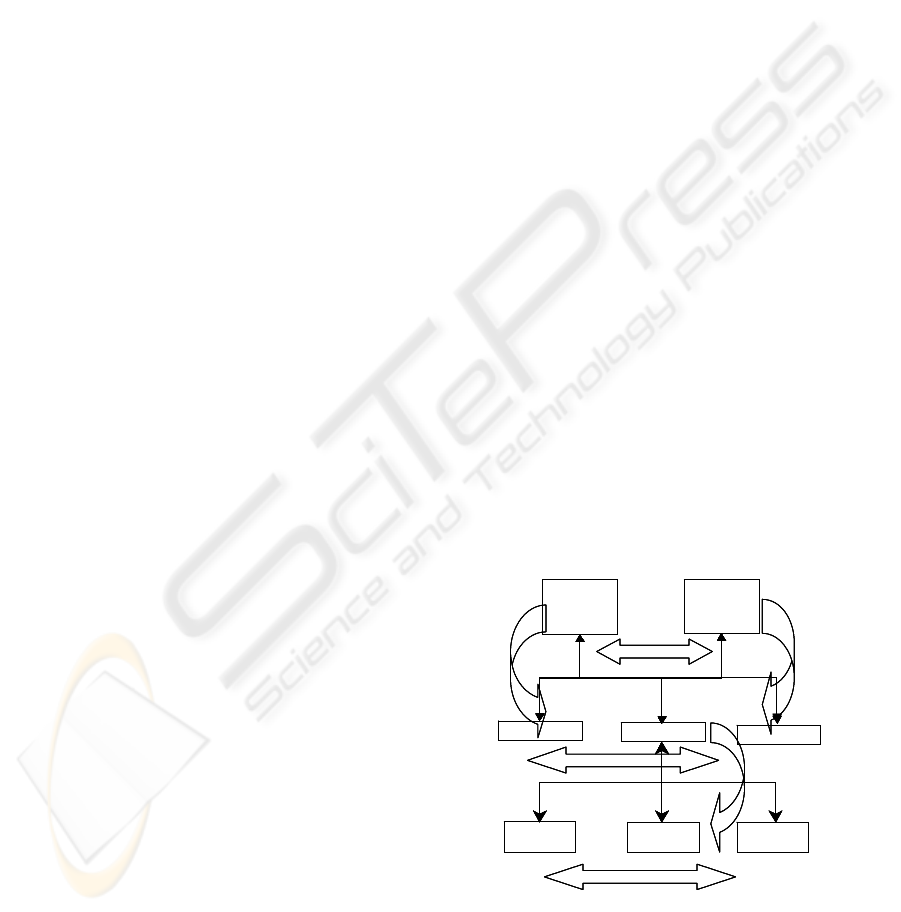
shown in Figure 2.

Figure 2: Game equilibrium strategies applied to a three-

level multiple decision control architecture with two

coordinators.

This structure has now two market coordinators,

one representing the market coordinator –supplier–,

Company-Player 1

Market

Coordinator

Supplier

Player

. . .

Level

Retaliatory sub -game

Pareto sub -game

Market

Coordinator

Consumer

Player

Nash sub -game

Dominant –

Marginal

sub -game

MCSS

MCSC

CSC

. . .

Manager-Unit

Player i,1

. . .

Level

Level2

Level

Retaliatory sub -game

Pareto sub -game

Paternalistic -

Solidary/Solitary

sub -game

Paternalistic -

Solidary/Solitary

sub -game

Stackelberg:

Leader -Follower

sub -game

Stackelberg:

Leader -Follower

sub -game

Nash sub -game

Dominant –

Marginal

sub -game

MCSS

MCSC

CSC

. . .

Company-Player i

Company-Player N

Manager-Unit

Player i,j

Player i,G

Manager-Unit

Company-Player 1Company-Player 1

Market

Coordinator

Supplier

Player

. . .

Level

Retaliatory sub -game

Pareto sub -game

Market

Coordinator

Consumer

Player

Market

Coordinator

Consumer

Player

Nash sub -game

Dominant –

Marginal

sub -game

MCSS

MCSC

CSC

. . .

Manager-Unit

Player i,1

. . .

Level

Level2

Level

Retaliatory sub -game

Pareto sub -game

Paternalistic -

Solidary/Solitary

sub -game

Paternalistic -

Solidary/Solitary

sub -game

Paternalistic -

Solidary/Solitary

sub -game

Paternalistic -

Solidary/Solitary

sub -game

Stackelberg:

Leader -Follower

sub -game

Stackelberg:

Leader -Follower

sub -game

Stackelberg:

Leader -Follower

sub -game

Stackelberg:

Leader -Follower

sub -game

Nash sub -game

Dominant –

Marginal

sub -game

MCSS

MCSC

CSC

. . .

Company-Player iCompany-Player i

Company-Player NCompany-Player N

Manager-Unit

Player i,j

Player i,G

Manager-Unit

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

188

MCSS, and another market coordinator –consumer–

, MCSC. The resulting structural mapping obtained

from a similar use of the four stages methodology,

and the corresponding equilibrium strategies

applicable to each sub-game identified, are shown in

Figure 2.

5 FINAL CONCLUSIONS

In this paper the strategic games matrix (SGM)

modeling framework is used as a tool for:

• Describing, characterizing, and mapping a wide

variety of conflicts of interests situations among

intelligent autonomous agents, both for hierarchical

and for non-hierarchical games, in an integrated

manner;

• Modeling, analysis and design of multilevel

multiple-agent control architectures in an integrated

manner, making explicit the obvious conflicts of

interests possibilities;

• Establishing a useful two-way conceptual bridge

between game theory and multiple-agent structures

analysis and design.

The SGM permits to evidence that, for a specific

real complex problem, we should be more concerned

with the choice of the right game to model,

than with

the right way to solve the game

, in spite of the

importance of these techniques.

REFERENCES

Alpcan, T., Başar, T., 2002. “A game-theoretic

framework for congestion control in general topology

networks”, Proc. 41st IEEE CDC, Las Vegas, Nevada.

Alpcan, T., Başar, T., 2004. “A game theoretic analysis of

intrusion detection in access control systems”, Proc.

IEEE CDC, Atlantis, Paradise Islands, Bahamas.

Başar, T., Olsder, G. J., 1999. Dynamic non-cooperative

game theory. Philadelphia, PA: SIAM, Series in

Classics in Applied Mathematics, 1999.

Bohacek, S., Hespanha, J. P., Obraczka, K., 2002. “Saddle

policies for secure routing in communication

networks”, Proc. 41

IEEE CDC, Las Vegas, Nevada.

Bottura C. P., Costa, E. A., 2004, “Business strategy

formulation modeling via hierarchical dynamic game”,

Proc. CSIMTA International Conference, Cherbourgh,

France.

Brandenburger, A. M., Nalebuff, B. J., 1995. “The right

game: Use of game theory to shape strategy”, Harvard

Business Review, pp.57-81.

Bryson Jr., A. E, Ho, Y. C., 1975. Applied optimal control.

Washington, DC: Hemisphere.

Castañón, D. A., Pachter, M., Chandler, P. R., 2004. “A

game of deception”, Proc. 43

IEEE, CDC, Atlantis,

Paradise Islands, Bahamas.

Costa Fº, J. T., Bottura, C. P., 1990. “Parallel optimal

hierarchical control using a MIMD architecture”,

Proc. 29

IEEE CDC, Honolulu.

Costa Fº, J. T., Bottura, C. P., 1991. “Hierarchical

multidecision making on a computer network with

distributed coordination and control”, Proc. 39

Annual Allerton Conference on Communication

Control and Computing, Urbana, IL, pp. 703-704.

Costa Fº., J. T., 1992. “Proposta para computação

assíncrona paralela e distribuída de estruturas especiais

de jogos dinâmicos”, Universidade Estadual de

Campinas, Faculdade de Engenharia Elétrica, Tese de

Doutorado, Campinas, SP, Brazil.

Costa, E. A., Bottura, C. P., 2006. “The Strategic Games

Matrix (SGM) as a new tool for strategic management

via game theory”, Sistemas & Gestão, 1 (1) pp. 17-41.

(in

http://www.latec.com.br/sg/arevista/Volume1/Numero

1/V1_1_index.htm ).

Cruz Jr., J. B., 1978. “Leader-follower strategies for

multilevel systems”, IEEE Trans. on Automatic

Control,

vol. AC-23 (2), pp. 244-255.

Dimarogonas, D. V., Kyriakopoulus, K. J., 2005. “A

feedback stabilization and collision avoidance scheme

for multiple independent nonholonomic non-point

agents”, Proc. 2005 IEEE Int. Symposium on

Intelligent Control, Limassol, Cyprus.

Haimes, Y. Y., Li, D., 1988. “Hierarchical multiobjective

analysis for large-scale systems: Review and current

status”, Automatica, vol. 24 (1), pp. 53-69.

Liu, Y., Galati, D. G., Simaan, M. A., 2004, “A game

theoretic approach to team dynamics and tactics in

mixed initiative control of automa-teams”, Proc. 43

IEEE CDC, Atlantis, Paradise Islands, Bahamas.

Rahimi-Kian, A. Tabarraei, H., Sadeghi, B., 2005.

“Reinforcement learning based supplier-agents for

electricity markets”, Proc. 2005 IEEE Int. Symposium

on Intelligent Control, Limassol, Cyprus.

Schelling, T. C., 1960. The strategy of conflict. New York,

NY: Harvard University Press.

Shao, J., Xie, G., Yu, J., Wang, L., 2005. “Leader-

following formation control of multiple mobile

robots”, Proc. 2005 IEEE Int. Symposium on

Intelligent Control, Limassol, Cyprus.

Shi, H., Wang, L., T. Chu, T., 2005. “Coordination of

multiple dynamic agents with asymmetric

interactions”, Proc. 2005 IEEE Int. Symposium on

Intelligent Control, Limassol, Cyprus.

THE STRATEGIC GAMES MATRIX AS A FRAMEWORK FOR INTELLIGENT AUTONOMOUS AGENTS

HIERARCHICAL CONTROL STRATEGIES MODELING

189