ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM

FOR MACHINING OPTIMIZATION PROBLEMS

Jean-Louis Vigouroux

1,2

, Sebti Foufou

, Laurent Deshayes

James J. Filliben

, Lawrence A. Welsch

and M. Alkan Donmez

Laboratoire Electronique, Informatique et Image (Le2i), University of Burgundy, Dijon, France

Currently a guest researcher at the National Institute of Standards and Technology (NIST), Gaithersburg, MD, USA

Laboratoire de M

ecanique et Ing

enieries, IFMA and University of Auvergne, Clermont-Ferrand, France

Information Technology Laboratory, at NIST, Gaithersburg, MD, USA

Manufacturing Engineering Laboratory, at NIST, Gaithersburg, MD, USA

Keywords:

Evolutionary algorithms, Experimental Algorithmics, Optimization of machining parameters.

Abstract:

In this paper, a novel method for tuning the design of an evolutionary algorithm (EA) is presented. The

ADT method was built from a practical point of view, for including an EA into a framework for optimizing

machining processes under uncertainties. The optimization problem studied, the algorithm, and the computer

experiments made using the ADT method are presented with many details, in order to enable the comparison

of this method with actual methods available to tune the desing of evolutionary algorithms.

1 INTRODUCTION

A mathematical framework for optimizing machining

processes with uncertainties, called the Robust Opti-

mizer, is currently being developed at the National In-

stitute of Standards and Technology (NIST), as a part

of the Smart Machining Systems Research Program

(Deshayes et al., 2005b). The goal of this frame-

work is to provide a process optimization capabil-

ity for machine-tools, integrated with the CAD/CAM

systems and the machine-tool controllers. Optimiza-

tion of machining processes is a difﬁcult task which

has been studied since the beginning of the last cen-

tury. As an example, the selection of optimal cut-

ting parameters involves the development of machin-

ing models, and optimization algorithms able to han-

dle those models. Taylor built the ﬁrst experimental

models in a seminal study (Taylor, 1907); after him

many different models and optimization algorithms

were developed. The class of optimization problems

encountered can be linear, convex non-linear, or non-

convex as shown by Deshayes et al. (Deshayes et al.,

2005a). For example in high-speed machining pro-

cesses, the constraint for chatter stability is deﬁned

by a non-convex function. Additionally, as shown

by Kurdi et al. (Kurdi et al., 2005), uncertainties

on model parameters may strongly inﬂuence the limit

contours of the constraint. As a consequence, the

framework under development must contain several

algorithms for optimization under uncertainties such

as robust linear programming, stochastic program-

ming, depending on the class of optimization prob-

lems. Vigouroux et al. (Vigouroux et al., 2007) pre-

sented a novel optimization algorithm to ﬁt into the

framework, for non-convex problems, by coupling an

evolutionary algorithm with interval analysis. EA are

algorithms from the Artiﬁcial Intelligence domain.

The main mechanism of EA is an iterative sampling

of candidate solutions to ﬁnd the optimal one, for

more information see the book of Yao (Yao, 1999).

The latest applications of EA include Pattern recog-

nition (Raymer et al., 2000), multi-disciplinary opti-

mization for car design (Rudenko et al., 2002). EA

have already been applied in machining by Wang et

al. (Wang et al., 2002) to a non-convex optimization

problem without uncertainties. EA are algorithms that

require tuning of their parameters to obtain optimal

results regarding execution time, convergence, and

accuracy. Moreover the parameters must be robust

for a range of similar problems.

The design of evolutionary algorithms, that is the

choice of an EA architecture and algorithm parame-

ters, robust to problem parameter changes, or adapted

to several problems is not straightforward. There-

240

Vigouroux J., Foufou S., Deshayes L., J. Filliben J., A. Welsch L. and Alkan Donmez M. (2007).

ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM FOR MACHINING OPTIMIZATION PROBLEMS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 240-247

DOI: 10.5220/0001624802400247

 SciTePress

fore, evolutionary algorithms have found applications

in speciﬁc optimization problems where the tuning of

the algorithm can be performed by the user. Several

methods to help this design were introduced recently

by Francois and Lavergne (Francois and Lavergne,

2001), Nannen and Eiben (Nannen and Eiben, 2006).

Nannen and Eiben were interested to design an evolu-

tionary system to study evolutionary economics. For

that complex system, EA are not just an optimization

algorithm but also a model for simulating evolution.

Therefore the EA used by Nannen and Eiben contain

much more parameters than the EA studied here: over

ten. Nannen and Eiben don’t have an alternate method

at hand to ﬁnd the optimum solution, mainly because

the EA studied does not perform optimization. To op-

timize the parameters of the EA, they built the CRE

method, by considering a trade-off between a per-

formance index,the average response of the EA, and

the average algorithm complexity, for 150 samples of

the algorithm parameters. To take in account simi-

lar problems, they let vary three problem parameters

and do 18 experiments. For each of them, an iterative

routine determines automatically the optimal values

of the algorithm parameters, based on the trade-off.

Then the optimal values of the parameters are found

as the average over all experiments.

The relevance of such methods is important to in-

tegrate EA in the Robust Optimizer. Machining prob-

lems have many parameters subject to changes. In

this paper, an alternative method to the CRE method,

the algorithm design tuning (ADT) method, is pre-

sented for helping the design of an EA for machin-

ing optimization problems. It makes use of statisti-

cal engineering tools not only to optimize the algo-

rithm parameters, but to modify the EA design in or-

der to avoid non-convergence. In the background of

the study are presented the example turning problem

used for building the Robust Optimizer, along with

the EA able to solve it, and some notions about ex-

perimenting with algorithms. Then the novel ADT

method is introduced along with experimental results

and a comparison with the CRE method.

2 BACKGROUND

2.1 Example Turning Problem for the

Robust Optimizer

An optimization problem consists of optimizing

an objective function while satisfying several con-

straints:

Minimize f(x)

subject to g

(x) ≤ 0 j = 1,2... p

where f is the objective function, g

a constraint func-

tion, and x is a vector of real variables, called a so-

lution of the problem. The vectors x

and x

deﬁne

the lower and upper bounds for the variables, and

are speciﬁed in some of the constraint equations g

These bounds deﬁne the search space.

The turning problem is a two-variable optim

ization problem, with a set of speciﬁc values for the

problem parameters. The variables and parameters

used in the problem are presented below:

f- Feed, mm/rev

Vc- Cutting speed, m/s

- Depth of cut, mm

min

- Minimum Feed, mm/rev

max

- Maximum Feed, mm/rev

min

- Minimum Cutting speed, m/s

max

- Maximum Cutting speed, m/s

Pu- Spindle power, W

Cu- Spindle torque, N ˙m

spe

- Workpiece desired surface roughness, µm

Ra- Workpiece surface roughness, µm

,δr

epsilon

- Constants in surface roughness equation

epsilon

- Tool nose radius, mm

- Cutting force, N

- Constant in cutting force equation

tc- Exponent in cutting force equation

T- Tool life, s

,Vc

- Constants in tool life equation

n,m,l- Exponents in tool life equation

cut

- Cutting time, s

parts

- Desired number of parts to cut per tool

A- Workpiece equivalent cutting surface, mm

- Workpiece average diameter, mm

- Workpiece equivalent length of cut, mm

The goal is to ﬁnd the optimal machining param-

eters, feed and speed, which maximize the material

removal rate (MRR) of one turning pass, considering

several process constraints. The two variables to be

optimized are the feed f and the cutting speed Vc.

The mathematical functions of the problem are de-

tailed below:

The objective function is deﬁned as the opposite of

MRR in order to solve a minimization problem

f( f,Vc) = −ap× f ×Vc (1)

The constraint function of minimum feed, C1:

( f,Vc) = f

min

− f (2)

The constraint function of maximum feed, C2:

( f,Vc) = f − f

max

(3)

To maximize an objective function is the same as to

minimize its negative opposite.

ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM FOR MACHINING OPTIMIZATION

PROBLEMS

241

The constraint function of minimum cutting speed,

C3:

( f,Vc) = Vc

min

−Vc (4)

The constraint function of maximum cutting speed,

C4:

( f,Vc) = V

−Vc

max

(5)

The constraint function of surface roughness, C5:

( f,Vc) = Ra( f) − Ra

spe

(6)

The constraint function of tool life, C6:

( f,Vc) = T( f,Vc) − t

cut

( f,Vc) (7)

The constraint function of Spidle power life, C7:

( f,Vc) = Pu− F

( f,Vc) ×V

(8)

Several functions have variables deﬁned by the equa-

tions presented below. The tool life equation is ob-

tained from Taylor’s work (Taylor, 1907):

T( f,Vc) = T

(9)

The cutting time, t

cut

, is obtained from the following

equation:

cut

( f,Vc) = N

parts

f × V

× 1000

, (10)

where A is obtained from the following equation:

A = π× D

× L

. (11)

The surface roughness equation is obtained from the

study by Deshayes et al. (Deshayes et al., 2005a):

Ra( f) = K

δr

epsilon

. (12)

The cutting force equation is obtained from an exper-

imental study by Ivester et al. (Ivester et al., 2006):

Fc( f) = Kc× f

1+tc

× ap. (13)

The original problem has parameter values given

in Table (1). For this original problem, the limit con-

tours of the constraint functions are represented in

Figure (1). Ten parameters of this problem can be

modiﬁed and are speciﬁed in Table (1). The parame-

ter ranges of this table are determined by knowledge

of machining and judgement.

2.2 Evolutionary Algorithms

In Darwin’s evolution theory (Darwin, 1859), a popu-

lation of individuals evolves over several generations.

The individuals with the best ﬁtness, determined by

their genes, are selected to breed; their children form

the next population. Since offspring of individuals

Table 1: Problem parameter ranges.

Parameter Original Minimum Maximum Factor

name value value value name

min

1.83 1.33 2.5 X1

max

7.5 6.5 10 X2

min

0.2 0.1 0.3 X3

max

0.6 0.5 0.8 X4

2 1 4 X5

2000 1800 2500 X6

Pu 15000 15000 20000 X7

72 60 80 X8

550 350 650 X9

spe

4.5 3 5 X10

with best ﬁtness should be better suited to survive

within their environment, the species improves. Thus,

over time and several generations, evolution leads to

the adaptation of the population to the environment.

This theory is used by the implemented Evolution-

ary Algorithm (EA). The optimization variables play

the role of the individuals’ genes. The EA is presented

as a class written in the Python language

. The con-

structor function of this class is presented below:

class EA:

def __init__(self):

self.gene_size=2

x1bounds=[0.2,0.6]

x2bounds=[1.83,7.5]

self.bounds = [x1bounds,x2bounds]

self.N = 50

self.alpha=0.4

self.z=20

The constructor sets the number of genes per individ-

ual (here two), the bounds of variables, the population

size N, the breeding parameter α, and the number of

generations z. The

run_algorithm

function contains

the algorithm steps and is presented here:

def run_algorithm():

population = population_initialize()

for i in range(self.z):

parent_population =

tournament_selection(population)

children_population =

breeding(parent_population)

population = children_population

return population[1]

Certain trade names and company products are men-

tioned in the text or identiﬁed in an illustration in order to

adequately specify the experimental procedure and equip-

ment used. In no case does such an identiﬁcation imply rec-

ommendation or endorsement by the National Institute of

Standards and Technology, nor does it imply that the prod-

ucts are necessarily the best available for the purpose. Ofﬁ-

cial contribution of the National Institute of Standards and

Technology; not subject to copyright in the United States.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

242

The EA has the following steps:

• Construction of the initial population. The

population_initialize

function, presented

below, outputs a ﬁrst population of N individuals

spread uniformly over the search space, by use of

random

function giving a number between zero

and one. The ﬁtness function, h, of one individ-

ual is computed with the static penalty method,

and is given in Equation (14). Michalewicz et al.

(Michalewicz et al., 1996) reviewed several meth-

ods that enable EA to handle optimization prob-

lems with constraints, and explain this method

with more details.

def population_initialize():

population = []

for i in range(self.pop_size):

population.append([])

for j in range(self.gene_size):

population[i].append(self.bounds[j][0]+

(self.bounds[j][1]

- self.bounds[j][0])*random())

population[i].append(fitness(population[i]))

return population

def fitness(genes):

result=h(genes)

return result

h(x) = −sf(x) +W ×

∑

j=1

(x) (14)

with

sf(x) =

f(x)

f(x

)

(15)

and

(x) =

(x)

)

if g

(x) ≤ 0, 0 else

(16)

W is the static penalty parameter. This parame-

ter controls the degradation of the ﬁtness function

when one or more constraints are violated. In this

article, the value of W is ten.

• Selection. The

tournament_selection

func-

tion, presented below, outputs a parent population

of N/2 individuals. These individuals are selected

by N/2 tournaments of size 2: for each tournament

two individuals are randomly picked in the pop-

ulation and their ﬁtness functions are compared.

The individual with the higher ﬁtness value wins

and is added to the parent population. The loser

re-enters the population and can eventually par-

ticipate in another tournament.

def tournament_selection(population):

pool_size=self.N/2

parent_population = []

for i in range(pool_size):

parent_population.append([])

match = Structure()

match.pool = sample(population,2)

match.knight1=match.pool[0]

match.knight2=match.pool[1]

if match.knight1[2] <match.knight2[2]:

match.winner = match.knight1

elif match.knight1[2] ==match.knight2[2]:

match.winner = match.knight1

else:

match.winner = match.knight2

parent_population[i] = match.winner

return parent_population

• Breeding. The

breeding

function, presented be-

low, outputs a new children population. Two indi-

viduals are randomly picked from the parent pop-

ulation. Two new individuals are created in a box.

The position of this box within the search space

is deﬁned by the two parents’ genes. The dimen-

sions of the box are deﬁned by both a breeding pa-

rameter called α and the two parents’ genes. This

process of creating individuals is called blend

crossover and was introduced by Eschelman and

Schaffer (Eschelman and Schaffer, 1993). It is re-

peated N/2 times in order to produce a children

population having N individuals.

def breeding(parent_population):

children_population = []

for i in range(self.pool_size):

parents = sample(parent_population,2)

parent1 = parents[0]

parent2 = parents[1]

children1 = []

children2 = []

for j in range(self.gene_size):

a= -self.alpha +(1+2*self.alpha)*random()

children1.append(a*parent1[j] +

(1-a)*parent2[j])

a= -self.alpha +(1+2*self.alpha)*random()

children2.append(a*parent1[j] +

(1-a)*parent2[j])

children1.append(fitness(children1))

children2.append(fitness(children2))

children_population.append(children1)

children_population.append(children2)

return children_population

At the next generation, this new population will

face again the selection step and the loop will con-

tinue until the number of generations z, is attained.

When the algorithm is stopped, the ﬁrst individual in

the population, with genes (x

), is picked. The

objective function MRR

is computed for this individ-

ual in Equation (17) and is the result output by the

algorithm.

MRR

= a

× x

(17)

For the original problem, the populations at several

generations are plotted in Figure (1). The initial pop-

ulation is represented by stars, the population at gen-

eration 2 is represented by circles, and the popula-

tion at generation 5 is represented by diamonds. The

ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM FOR MACHINING OPTIMIZATION

PROBLEMS

243

evolution of the center of gravity of the population

over several generations deﬁnes a track represented

by crosses and dashed lines. This algorithm has three

inﬂuential parameters: the breeding parameter α, the

population size N, and the number of generations, z.

Tuning of these parameters is required to enhance the

performance of the algorithm.

Figure 1: Populations at several generations during one run

of the EA.

2.3 Experimental Algorithmics

Experimental Algorithmics refer to the study of al-

gorithms through a combination of experiments and

classical analysis and design techniques.

Since EA are randomized algorithms, their results

are unequal run after run, even though all parameters

may remain the same. Therefore, it is necessary to run

the EA several times to report an average result. Thus,

the computational expense associated with the tun-

ing of the algorithm may become important. Statis-

tical techniques such as design of experiments and re-

sponse surface methodology avoid this computational

expense and are presented in (NIST/SEMATECH,

2006) and (Box et al., 1978).

A computer experiment refers here to a run of the

EA with a set of algorithm parameters and a set of

problem parameters. With the design of experiments,

the problem parameters are renamed factors, see

Table (1); a design stands for a set of experiments,

with each experiment having a speciﬁc combination

of factor levels. When considering only two levels

of variation for each problem parameter, the low

settings and the high settings presented in Table

(1), there are 1024 possible combinations. A full

factorial design is a set with all possible factor levels

combinations, here 2

= 1024. A more efﬁcient

design is an orthogonal fractional factorial design

(NIST/SEMATECH, 2006), with only 128 runs, ten

percent of the full factorial design.

According to the response surface terminology

(Box et al., 1978), the measures made during the ex-

periments are referred to as response variables.

For the design of the EA, three response variables

are considered:

• y

is an index deﬁning the accuracy of the EA:

MRR

∗

(18)

where MRR

∗

is the optimal material removal rate

of the problem, corresponding to the optimal so-

lution. MRR

∗

can be obtained graphically or

by another optimization algorithm able to ﬁnd

it. Since MRR is an increasing function, The ex-

pected range of y

is between 0 and 1. If the value

of y

is greater, the result MRR

output by the al-

gorithm is unacceptable and it means that the al-

gorithm did not converge.

• y

is the count of non-convergence cases af-

ter several runs of the algorithm. Those non-

convergence cases are detected by values of y

higher than 1.

• y

is a time measure in seconds, related to the ex-

ecution time of the EA.

The set-up of the computer experiments is given:

The EA is implemented with Matlab software on a

personal computer. The computer processor is an In-

tel Pentium 4 with a frequency of 3.80 GHz, running

with a memory of size 2 GB. The measure of y

made using Matlab’s cputime function.

The random function used to generate the neces-

sary random behaviors in the algorithm is Matlab’s

random function with the Seed method. It gener-

ates a pseudo-random number between 0 and 1. Af-

ter a certain number of calls, 2

− 1, the function

repeats itself. This function takes as the argument a

number called the seed. The seed deﬁnes the internal

state of the function and, with the same seed, the ran-

dom function generates the same sequence of random

numbers. Therefore, all the seeds used in the experi-

ments were recorded and stored, giving the possibility

to reproduce exactly the same experimental results.

Each computer experiment was replicated ten times

with different seeds.

Once the computer experiments have been made,

the Exploratory Data Analysis (EDA) techniques

(Tukey, 1977) can be used to explore the results.

These techniques allow to ferret out interesting at-

tributes of the result data. The Dataplot statistical en-

gineering software was used in this study to perform

EDA. Sensitivity analysis is a technique that allows to

order the problem parameters according to the effect

of their variation on the response. The order of the

parameter can be deduced from a plot called the main

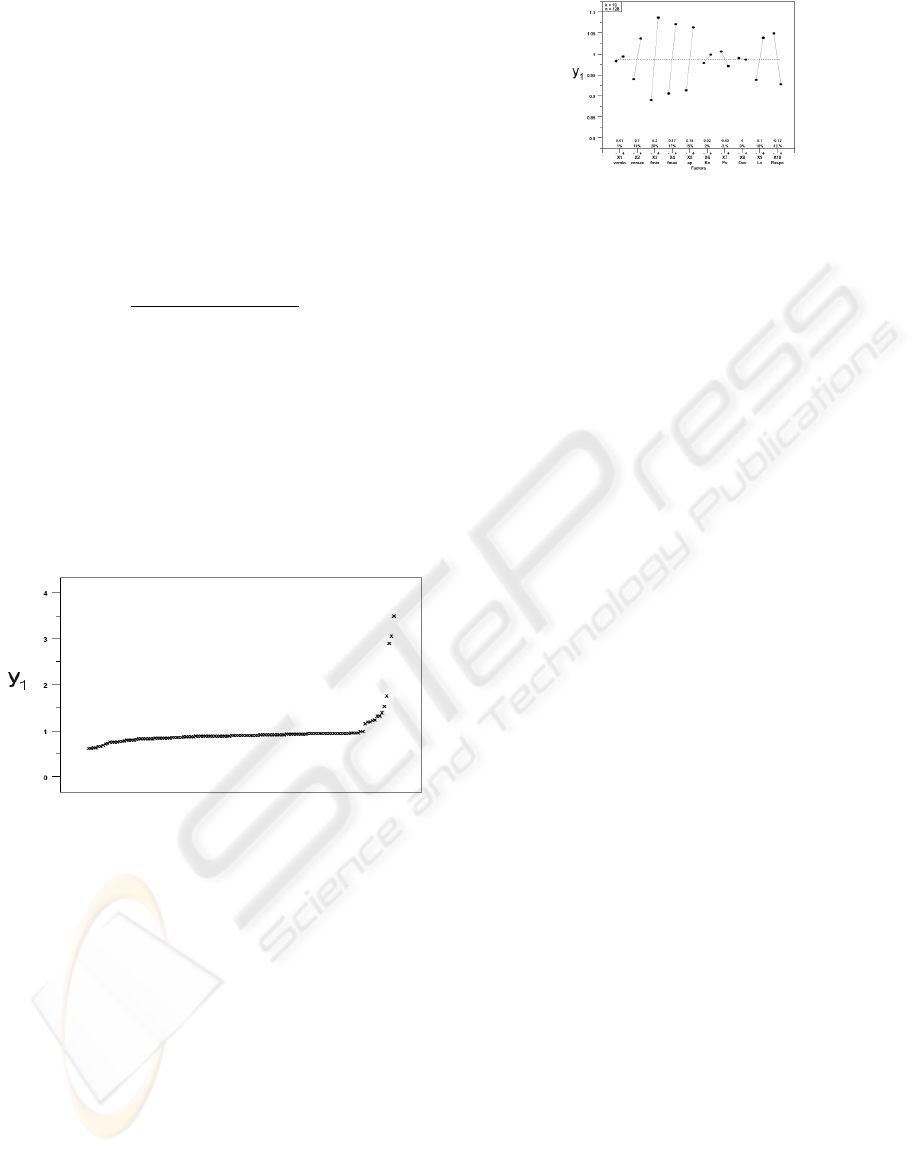
effect plot. An example plot is shown in Figure (3).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

244

3 THE ADT METHOD

3.1 Step 1: Preliminary Exploratory

Data Analysis

The ﬁrst step of the methodology is to perform an

exploratory analysis. The goal is to see how much

the algorithm performances vary, and to establish if

the algorithm needs any modiﬁcations of its architec-

ture. This analysis requires performing computer ex-

periments with a set of algorithm parameters (α,N,z),

according to the orthogonal fractional

factorial design

introduced previously. This step requires a special

plot of the response y

: the responses of all exper-

iments are ordered and plotted, as shown in Figure

(2). The experiments where the algorithm does not

converge are detected by values of y

exceeding one.

The reason for non-convergence can be discovered by

plotting the limit contours of the constraints for the

case with non convergence, similarly to Figure (1)

presented previously. Then the algorithm architecture

may be modiﬁed, in order to be adapted to the non-

convergence cases.

Figure 2: Ordered data plot of response y

for the ex-

ploratory analysis of the set (α = 0.4, N = 40,z = 20).

3.2 Step 2: Sensitivity Analysis

This step is optional. This step may only be re-

quired if the problem has more than two optimiza-

tion variables, where it may be impossible to plot

the limit contours of the constraints for the case with

non-convergence. In that case the reason for non-

convergence cannot be easily discovered. The sen-

sitivity analysis allows to determine the most impor-

tant problem parameters affecting the response y

The main effect plot in Figure (3) shows the varia-

tion of the response y

depending on the variation of

the problem parameters.

Figure 3: Main effect plot of response y

for the sensitivity

analysis of the set (α = 0.4, N = 40,z = 20).

3.3 Step 3: Optimization

In this step the algorithm parameters are

optimized(α,N,z). α,N,z can be chosen respec-

tively in the range [20, 200],[0.1, 0.9] and [10,

50]. Given a set (α,N,z), a sensitivity analysis is

performed as previously discussed, but the results of

each computer experiment are now three responses,

, y

, and y

. The goal is to optimize the average

values of the responses: maximize ¯y

, minimize ¯y

minimize ¯y

First, only the ﬁrst objective ¯y

is considered.

Since the computational expense of the sensitivity

analysis necessary to compute ¯y

is high, only a small

number of sets (α,N,z) can be investigated. The re-

sponse surface methodology is applied to ﬁnd the best

set (α,N,z). Starting with an initial guess (α

several other sets in the neighborhood are tested,

whose values are deﬁned by an orthogonal full fac-

torial design. This design has 3 factors and 11 exper-

iments. The choice of the parameter ranges, centered

around the set (α

), is left to the user.

The result ¯y

of each tested set (α,N,z) can be vi-

sualized as a cube, as shown in Figure (4). From the

analysis of the cube, a new center set (α

) is

chosen, to explore the space in the region where the

optimum value of ¯y

, ¯y

∗

, could be located. Again,

computer experiments are performed with the same

design but with different parameter ranges, in order

to acquire the new cube with center (α

). This

iterative process can be repeated as long as needed in

order to ﬁnd ¯y

∗

. The cubes for the objectives ¯y

and

¯y

can be acquired at the same time, although the op-

timum values for these objectives are not found. This

method enables one to explore the spaces ¯y

and ¯y

functions of variables (α,N,z). After the three objec-

tive spaces have been explored, the user is able to pick

a set (α,N,z), that has good values ¯y

, ¯y

, and ¯y

, al-

though not optimal. This set represents a compromise

between best accuracy, best convergence, and best ex-

ecution time.

ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM FOR MACHINING OPTIMIZATION

PROBLEMS

245

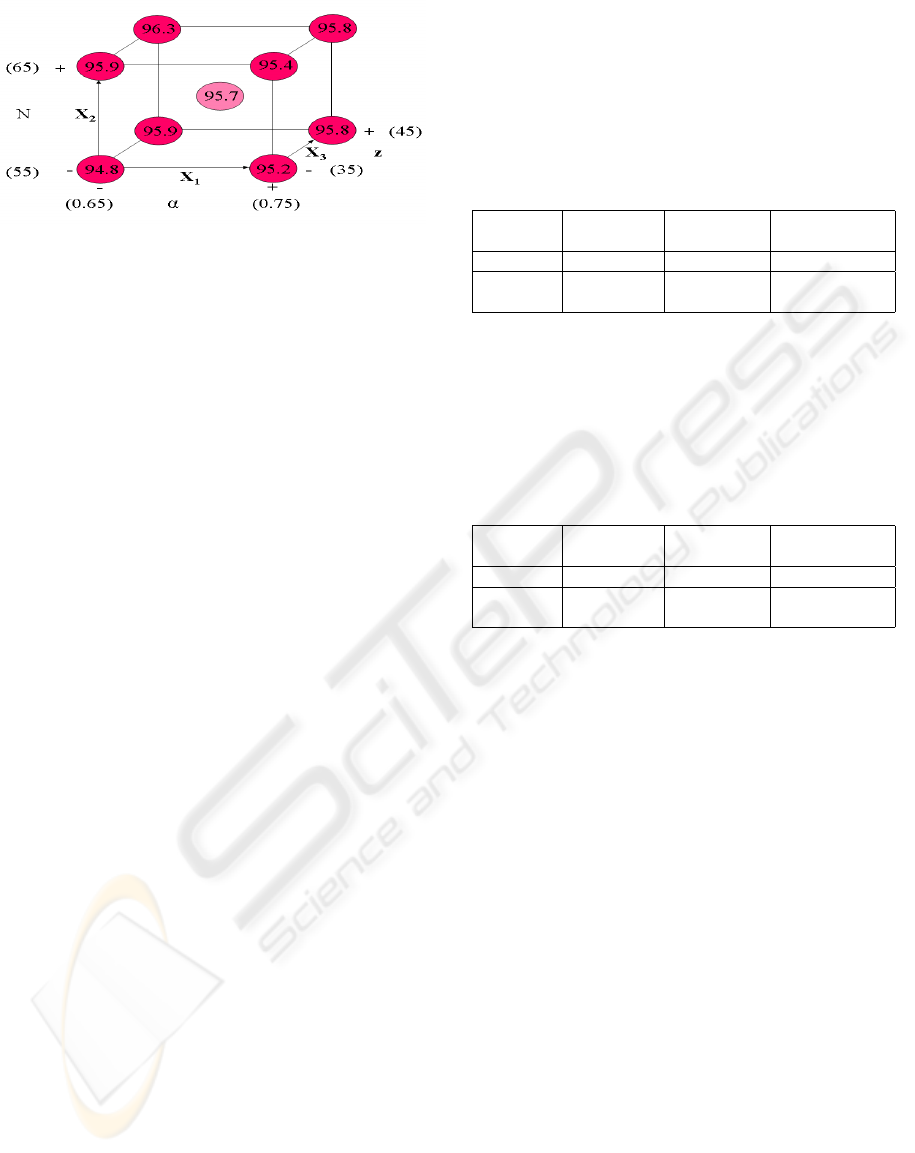
Figure 4: The responses ¯y

multiplied by 100 for the cube

with center (α

= 0.7, N

= 60, z

= 40).

3.4 Validation of the Optimized

Algorithm

The algorithm is optimized with a sample of prob-

lem parameter combinations and a sample of seeds.

This sample can be termed a training data set, and an

analogy can be drawn with the training of neural net-

works. Now the performance results of the algorithm

must be veriﬁed with a new sample of data: the vali-

dation data set.

In order to compare the average performance re-

sults, a validation data set of the same size as the train-

ing data set must be chosen. A different sampling of

the problem parameter combinations is made. A Latin

hypercube sampling is used with the same size as the

orthogonal design presented in Section (2.3): 128 val-

ues for each of the ten factors. A new sample of 100

different seeds is also picked and stored. The sensitiv-

ity analysis can be replicated ten times with the new

data and the results compared.

3.5 Results

The preliminary exploratory analysis was performed

on the set (α = 0.4, N = 40, z = 20). The ordered data

plot of response y

, shown in Figure (2), revealed non-

convergence cases, detected on the right of the plot by

values exceeding one. The limit contours of the con-

straints were plotted for some of the non-convergence

cases, and it was discovered that the initialization step

was not adapted. To avoid this problem, it was de-

cided to change the initialization so that the ﬁrst pop-

ulation is spread in the lower left quarter of the search

space. The sensitivity analysis, shown in Figure (3),

was performed, but all the information provided by

this step was already known from the plots of the ﬁrst

step.

In the third step, optimization was performed with

an initial guess (α

= 0.7, N

= 60, z

= 40). Af-

ter three iterations, it was found that ¯y

∗

should have

a value around 0.97, and a good conﬁdence was ac-

quired about the knowledge of the three objective

spaces. The set of algorithm parameters selected is

(α = 0.6, N = 60, z = 40). The results of a sensitiv-

ity analysis of this set, replicated ten times, is shown

in Table (2). During the validation step, a compari-

Table 2: Optimization step: results for the set (α = 0.6,N =

60,z = 40) with the training data set.

Response Response Response

variable ¯y

(s)

average 0.950 1 1.130

standard 0.002 1.05 0.003

deviation

son was made between the results obtained with the

training data set and the results obtained with the val-

idation data set. The later results presented in Table

(3) are slightly better. Therefore, the training method

used to tune the algorithm seems to be sound.

Table 3: Validation step: results for the set (α = 0.6,N =

60,z = 40) with the validation data set.

Response Response Response

variable ¯y

(s)

average 0.966 0 1.123

standard 0.001 0.00 0.002

deviation

3.6 Comparison with the Cre Method

The ADT method was developped for the turning

problem of the Robust Optimizer. From this point of

view the EA has few parameters, three, and quite a lot

of problem parameters, ten. On the contrary, the CRE

method considers many EA parameters and few prob-

lem parameters. The reason why the CRE method

does not consider many problem parameters may be a

reason of time consumed to perform the experiments,

as indicated in the paper by Nannen and Eiben (Nan-

nen and Eiben, 2006). The ADT method required also

a lot of time to perform the experiments. For both

methods, increasing the number of algorithm param-

eters and problem parameters considered is a prob-

lem, so the complexity of the CRE and ADT methods

should be determined and compared.

The CRE method relies on information theory to

determine the importance of the algorithm parame-

ters. This point is not adressed by the ADT method.

During the study, it was decided to remove the muta-

tion parameter from the algorithm by studying videos

showing the populations evolve over the search space,

during several iterations. This kind of decision was

made possible because of the low dimension of the

optimization problem studied: only two variables.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

246

The ADT method enables to optimize very practi-

cal responses of EA: the execution time, the number

of non-convergence cases, the accuracy. For the last

objective, accuracy, one needs to know the optimal

solution for each optimization problem. This is possi-

ble graphically only for low dimension optimization

problems. For optimization problems of higher di-

mension, an alternative optimization algorithm must

be used.

Since this method was developped concurrently

with the CRE method, an experimental comparison

of the two methods was not possible. However all de-

tails are given in this paper to perform such a study.

4 CONCLUSION

The novel ADT method presented here enables tun-

ing the design of an EA for optimizing a turning pro-

cess with uncertainties. The ADT method also en-

ables the algorithm designer to manage several per-

formance objectives. The method is an alternative

method to the CRE method, and focuses on the practi-

cal objectives of accuracy, non-convergence and exe-

cution time. In the future, the two methods need to be

compared. For the Robust Optimizer, an optimization

problem involving a milling process needs to be con-

sidered, to see if the ADT method enables to design an

EA for optimizing different kinds of machining pro-

cesses, or not.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the support

and assistance of Robert Ivester, David Gilsinn, Flo-

rian Potra, Shawn Moylan, and Robert Polvani, from

the National Institute of Standards and Technology.

REFERENCES

Box, G. E. P., Hunter, W. G., and Hunter, J. S. (1978).

Statistics for Experimenters. John Wiley.

Darwin, C. (1859). On the origin of species by means of

natural selection. John Murray.

Deshayes, L., Welsch, L., Donmez, A., and Ivester, R. W.

(2005a). Robust optimization for smart machining

systems: an enabler for agile manufacturing. In Pro-

ceedings of IMECE2005: 2005 ASME International

Mechanical Engineering Congress & Exposition.

Deshayes, L., Welsch, L., Donmez, A., Ivester, R. W.,

Gilsinn, D., Rohrer, R., Whitenton, E., and Potra, F.

(April 3-5, 2005b). Smart machining systems: Issues

and research trends. In Proceedings of the 12th CIRP

Life Cycle Engineering Seminar.

Eschelman, L. and Schaffer, J. D. (1993). Real-coded

genetic algorithms and interval-schemata. Morgan

Kaufmann.

Francois, O. and Lavergne, C. (2001). Design of evolution-

ary algorithms-a statistical perspective. IEEE Trans-

actions on Evolutionary Computation, 5(2):129–148.

Ivester, R. W., Deshayes, L., and McGlauﬂin, M.

(2006). Determination of parametric uncertainties

for regression-based modeling of turning operations.

Transactions of NAMRI/SME, 34.

Kurdi, M. H., Haftka, R. T., Schmitz, T. L., and Mann,

B. P. (November 5-11, 2005). A numerical study of

uncertainty in stability and surface location error in

high-speed milling. In IMECE ’05: Proceedings of

the IMECE 2005, number 80875. ASME.

Michalewicz, Z., Dasgupta, D., Riche, R. L., and Schoe-

nauer, M. (1996). Evolutionary algorithms for con-

strained engineering problems. Computers & Indus-

trial Engineering Journal, 30(2):851–870.

Nannen, V. and Eiben, A. (2006). A method for parameter

calibration and relevance estimation in evolutionary

algorithms. In GECCO ’06: Proceedings of the 8th

annual conference on Genetic and evolutionary com-

putation, pages 183–190, New York, NY, USA. ACM

Press.

NIST/SEMATECH (2006). Nist/sematech

engineering statistics handbook,

http://www.itl.nist.gov/div898/handbook/.

Raymer, M., Punch, W., Goodman, E., Kuhn, L., and Jain,

A. (2000). Dimensionality reduction using genetic

algorithms. IEEE Trans. Evolutionary Computation,

4:164–171.

Rudenko, O., Schoenauer, M., Bosio, T., and Fontana, R.

(Jan 2002). A multiobjective evolutionary algorithm

for car front end design. Lecture Notes in Computer

Science, 2310.

Taylor, F. N. (1907). On the art of cutting metals. Transac-

tions of the ASME, 28:31.

Tukey, J. W. (1977). Exploratory data analysis. Addison-

Wesley.

Vigouroux, J., Deshayes, L., Foufou, S., and Welsch, L.

(2007). An approach for optimization of machin-

ing parameters under uncertainties using intervals and

evolutionary algorithms. In Proceedings of the ﬁrst In-

ternational Conference on Smart Machining Systems,

to appear.

Wang, X., Da, Z. J., Balaji, A. K., and Jawahir, I. S. (2002).

Performance-based optimal selection of cutting con-

ditions and cutting tools in multipass turning opera-

tions using genetic algorithms. International Journal

of Production Research, 40(9):2053–2059.

Yao, X. (1999). Evolutionary Computation: Theory and

Applications. World Scientiﬁc.

ON TUNING THE DESIGN OF AN EVOLUTIONARY ALGORITHM FOR MACHINING OPTIMIZATION

PROBLEMS

247