DIRECTIONAL CHANGE AND WINDUP PHENOMENON
Dariusz Horla
Poznan University of Technology
Institute of Control and Information Engineering
Division of Control and Robotics
Keywords:
Windup phenomenon, Directional change, Control limits, Multivariable systems.
Abstract:
The paper addresses two inherently connected problems, namely: windup phenomenon and directional change
in controls problem for multivariable systems. By comparing two ways of performing anti-windup compen-
sation and two different saturation modes a new definition of windup phenomenon for multivariable systems
has been obtained, changing definitions present in the literature. It has been shown that avoiding directional
change does not have necessarily to mean that windup phenomenon has been avoided too.
1 INTRODUCTION
Consideration of control limits is crucial for achieving
high control performance (Peng et al., 1998). There
are two ways in which one can consider possible con-
straints during synthesis of controllers, e.g. imposing
constraints during the design procedure, what leads
to difficulties with obtaining explicit forms of control
laws. The other way is to assume the system is linear
and, subsequently, having designed the controller for
unconstrained system – impose constraints, what re-
quires then additional changes in control system due
to presence of constraints.
A situation when because of, e.g., constraints (or,
in general, nonlinearities) internal controller states do
not correspond to the actual signals present in the con-
trol systems is referred as windup phenomenon (Wal-
gama and Sternby, 1993; Horla, 2004). It is obvious
that due to control signal constraints not taken into
account during a controller design stage, one can ex-
pect inferior performance because of infeasibility of
computed control signals.
There are many methods of compensating the
windup phenomenon (Peng et al., 1998; Walgama and
Sternby, 1993), but a few work well enough in the
case of multivariable systems. In such a case, apart
from the windup phenomenon itself, one can also
observe directional change in the control vector due
to, say, different implementation of constraints, what
could affect direction of the original, i.e. computed,
control vector.
The paper aims to compare two strands in con-
troller design subject to constraints, as mentioned be-
fore, and two ways of anti-windup compensation with
respect to directional change in controls.
As a result, a new definition of windup phe-
nomenon will be obtained with respect to directional
change in controls, which in the case of multivariable
systems cannot be omitted.
2 ANTI-WINDUP
COMPENSATION
There are two general schemes in anti-windup com-
pensation (AWC) connected with controller design.
If the controller has been designed for the case of a
linear plant, i.e. with no constraints, introducing them
would require certain (most often) heuristic modifi-
cations in the control law that usually feed back the
difference in between computed v
t
and constrained
control vector u
t
. This is referred in the literature as a
posteriori AWC (Horla, 2006a; Horla, 2006b).
The second AWC is incorporated implicitly into
the controller, i.e. when controller generates feasible
control vector only (belonging to the domain D of
all control vectors for which a certain control perfor-
369
Horla D. (2007).
DIRECTIONAL CHANGE AND WINDUP PHENOMENON.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 369-374
DOI: 10.5220/0001622903690374
Copyright
c
 SciTePress

mance index J
t
is of finite value), what is addressed
as a priori AWC.
3 A POSTERIORI AWC
One of the most popular AWCs (Peng et al., 1998) are
those based on the RST equation, which in the case of
multivariable systems is of the form (Horla, 2004)
R(q
−1
)v
t
= −S(q
−1
)y
t
+ T(q
−1
)r
t
, (1)
where
R(q
−1
) = I + R
1
q
−1
+ ··· + R
nR
q
−nR
,
S(q
−1
) = S
0
+ S
1
q
−1
+ ··· + S
nS
q
−nS
,
T(q
−1
) = T
0
+ T
1
q
−1
+ ··· + T
nT
q
−nT
are controller polynomial matrices of appropriate
sizes, designed for the unconstrained case, y
t
∈ R
p
is
the output vector, v
t
∈ R
m
is the control vector, d > 0
is a dead-time.
When the nonlinearities, such as control limits,
are taken into consideration the computed vector v
t
is different from the constrained, i.e. applied, control
vector u
t
. In such a case one can modify the control
law according to AWC schemes given below (Horla,
2004; Peng et al., 1998).
• Deadbeat AWC (DB)
v
t
= (I −R(q
−1
))u
t
−S(q
−1
)y
t
+T(q
−1
)r
t
. (2)
The controller is fed back with the constrained
control vector, thus no lack of consistency occurs.
• Generalised AWC (G)
A matrix A
o
(q
−1
) of observer polynomials with
nA
o
≤ nR is added
A
o
(q
−1
)v
t
= (A
o
(q
−1
) − R(q
−1
))u
t
−
−S(q
−1
)y
t
+ T(q
−1
)r
t
. (3)
• Conditioning technique AWC (CT)
The control vector and reference signal are com-
puted as
v
t
= (I − R(q
−1
))u
t
− S(q
−1
)y
t
+
+(T(q
−1
) − T
0
)r
r
t
+ T
0
r
t
, (4)
r
r
t
= r
t
+ T
−1
0
(u
t
− v
t
). (5)
A special case of CT is Modified conditioning
technique AWC (MCT) where instead of T
−1
0
there is an inversion of matrix (T
0
+ϒ)
−1
which is
responsible for the rate of modification of the ref-
erence vector subject to constraints.
In the CT case, often outputs that were intended
to me unmodified, are modified due to condition-
ing technique. The latter is a result of directional
change, that is given rise by anti-windup compen-
sation. The two issues are therefore connected.
• Generalised conditioning technique AWC (GCT)
The restoration of the consistency is performed by
modifying the filtered reference vector, i.e. com-
puting the so-called feasible filtered reference
vector,
v
t
= (I − Q(q
−1
)R(q
−1
))u
t
+
+T
2,0
r
f,t
+ (T
2
(q
−1
)L(q
−1
) − T
2,0
)r
r
f,t
+
−Q(q
−1
)S(q
−1
)y
t
. (6)
r
f,t
= Q(q
−1
)L(q
−1
)
−1
T
1
(q
−1
)r
t
, (7)
r
r
f,t
= r
f,t
+ T
−1
2,0
(u
t
− v
t
), (8)
Where T = T
2
T
1
with monic T
1
, and nonsingular
T
2,0
.
4 DEFINITION OF WINDUP
PHENOMENON IN
MULTIVARIABLE SYSTEMS
Currently, one can meet the following definition of
windup phenomenon in multivariable systems with
its connections to directional change (Walgama and
Sternby, 1993):
Solving the windup phenomenon problem does not
mean that constrained control vector is of the same
direction as computed control vector.
On the other hand, avoiding directional change in
control enables one to avoid windup phenomenon.
In further parts of this paper, it has been shown
where the latter definition holds, and in what cases it
is invalid.
5 DIRECTIONAL CHANGE
PHENOMENON, AN EXAMPLE
Let us suppose that two-input two-output system is
not coupled and both loops are driven by separate con-
trollers (with no cross-coupling). The system output
y
t
is to track reference vector comprising two sinusoid
waves. It corresponds in the (y
1
,y
2
) plane to drawing
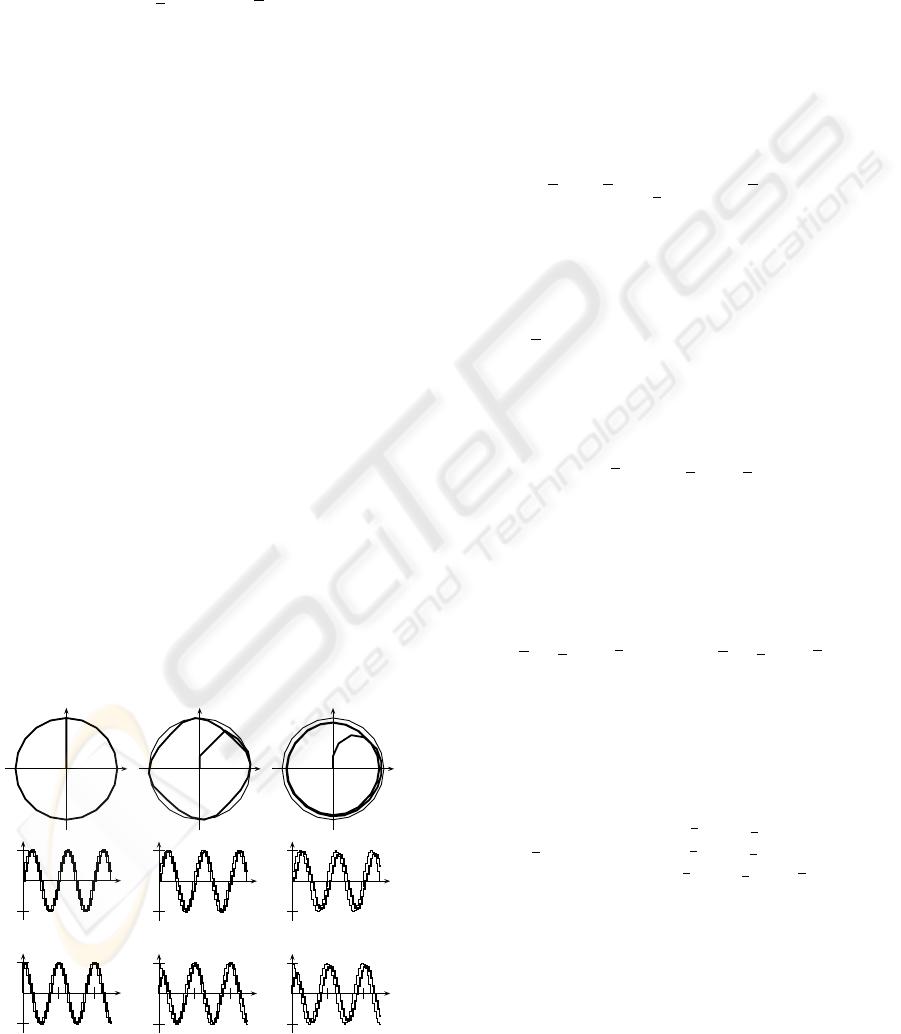
a circular shape.
As it can be seen in the Fig. 1a, the unconstrained
system performs best, whereas in the case of cut-off
saturation of both elements of control vector (Fig. 1b)
the tracking performance is poor. In the applica-
tion for, e.g., shape-cutting performance of the system
from Fig. 1c is superior. Nevertheless, it is to be borne
in mind that the system is always perfectly decoupled.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
370

6 PLANT MODEL, CONTROL
PROBLEM
The following multivariable CARMA plant model
will be of interest
A(q
−1
)y
t
= B(q
−1
)u
t−d
, (9)
with left co-prime polynomial matrices
A(q
−1
)=I+

−1.4 −0.1
0.1 −1.0

q
−1
+

0.49 0
0 0.25

q
−2
,
B(q
−1
) = I + diag
{
0.5, 0.5
}
q
−1
and d = 1.
The plant is cross-coupled and comprises fourth-
order matrices in the transfer matrix representation
(being stable and minimumphase).
6.1 RST Controller (a Posteriori AWC)
It is assumed that the plant is controlled by a multi-
variable pole-placement controller with characteristic
polynomial matrix
A
M
(q
−1
) = I + diag
{
−0.5, −0.5
}
q
−1
.
The controller is given in RST structure with polyno-
mial matrices R(q
−1
) and S(q
−1
) resulting from Dio-
phantine equation
A(q
−1
)R(q
−1
) + q
−d
B(q
−1
)S(q
−1
) = A
M
(q
−1
)A
o
(q
−1
),
(10)
with A
o
(q
−1
) = I − 0.2Iq
−1
, T(q
−1
) = KA
o
(q
−1
),
A
M
(1) = B(1)K.
Having imposed control limits upon the RST con-
troller requires implementing a posteriori AWC tech-
niques in order to restore good performance quality.
y
1,t
y
2,t
a)
y
1,t
y
2,t
b)
y
1,t
y
2,t
c)
20 40
0
1
−1
t
y
1,t
20 40
0
1
−1
t
y
1,t
20 40
0
1
−1
t
y
1,t
20 40
0
1
−1
t
y
2,t
20 40
0
1
−1
t
y
2,t
20 40
0
1
−1
t
y
2,t
Figure 1: a) unconstrained system, b) cut-off saturation,
c) direction-preserving saturation.
6.2 Optimised Controller (a Priori
AWC)
In comparison, the RST pole-placement controller
performance will be compared with a priori AWC
controller, namely multivariable pole-placement con-
troller utilising the theory of predictive control and
convex optimisation techniques.
In order to enable such a comparison, the pre-
dictive controller has been deprived of all its advan-
tages – the prediction horizon has been chosen as one
step, thus the optimal constrained control vector is
searched (Horla, 2006a; Horla, 2006b)
u
⋆
t
: J
t
(u
⋆
t
) = inf
u
t
∈D(J
t
)
{
J
t
(u
t
)
}
,
where its jth component has been symmetrically con-
strained
|u
j,t
| ≤ α
j
,
where
u
t
=

u
1,t
u
2,t
··· u
m,t

T
.
The performance index has been chosen as a sum
of squared tracking errors resulting from a reference
model output
J
t
=



r
M,t+d
− ˆy
t+d
−
ˆ
ˆy
t+d



2
2
, (11)
where one-step (d = 1) prediction of system output
comprises as in (11) forced and free-response output
vectors.
The performance index can be rewritten into
quadratic form
J
t
=

Gu
t
+
ˆ
ˆy
t+d
− r
M,t+d

T

Gu
t
+
ˆ
ˆy
t+d
− r
M,t+d

,
(12)
and the optimisation can be performed with the use of
its linear matrix inequality (LMI) form with the last
two LMIs responsible for control constraints, as be-
low
min γ
s.t.





I ⋆
u
T
t
(G
T
G)
1/2



γ− (r
M,t+d
−
ˆ
ˆy
t+d
)
T
×
×(r
M,t+d
−
ˆ
ˆy
t+d
)+
+2(r
M,t+d
−
ˆ
ˆy
t+d
)
T
Gu
t








≥ 0,
diag
{
α
1
− u
1,t
,. . ., α
m
− u
m,t
}
≥ 0,
diag
{
α
1
+ u
1,t
,. . ., α
m
+ u
m,t
}
≥ 0,
(13)
where ⋆ detones a symmetrical entry, and G is an
impulse-response matrix.
DIRECTIONAL CHANGE AND WINDUP PHENOMENON
371

7 SIMULATION STUDIES
The simulations have been performed for two con-
trollers: for a pole-placement controller with a group
of a posteriori AWCs and LMI-based predictive pole-
placement controller.
In order to evaluate control performance con-
nected with anti-windup compensation performance
the following performance indices have been intro-
duced
J =
1
N
2
∑
i=1
N
∑
t=1
|r
i,t
− y
i,t
|, (14)
ϕ =
1
N
N
∑
t=1
|ϕ(v
t
) − ϕ(u
t
)| [
◦
], (15)
where (14) corresponds to mean absolute tracking er-
ror on both outputs and (15) is a mean absolute di-
rection change in between computed and constrained
control vector.
The control vector has been constrained in all
cases to α
1
= ±0.2 on the first input and α
2
= ±0.3
for the second output. The reference vector is a
square-wave signal of amplitude ±1 and simulation
horizon N = 150.
Performance indices have been given in the Tab. 1.
Table 1: Performance indices for a) cut-off saturation,
b) direction-preserving saturation.
a)
− DB G CT MCT GCT
J 1.1539 1.1539 1.1539 1.1539 1.1536 1.1516
ϕ 0.9003 0.9004 1.1861 1.1862 1.1093 1.5495
b)
− DB G CT MCT GCT
J 1.1772 1.1672 1.1677 1.1677 1.1670 1.1655
ϕ 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
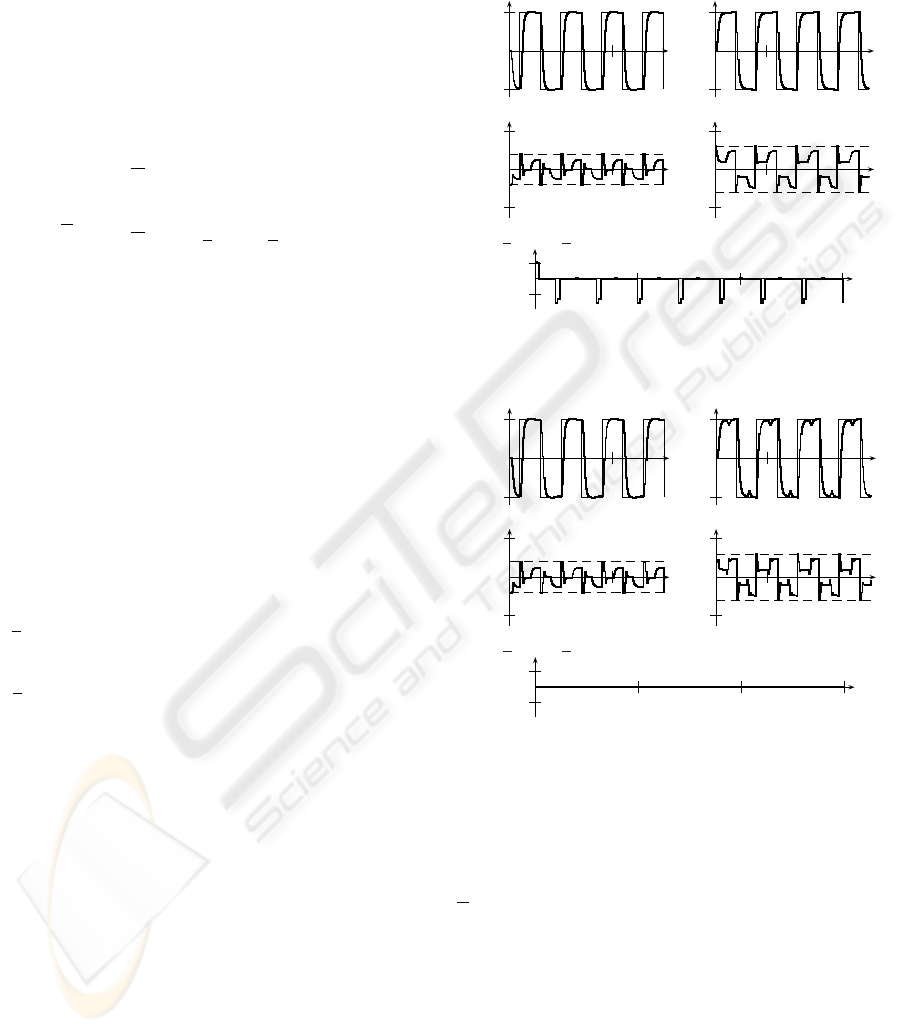
As it can be seen from Tab. 1a, and Figs. 4, 5,
cut-off saturation causes directional change, which is
visible during reference vector changes. It is neces-
sary to alter the decoupling of the plant, in order to
restore high control performance. As it can be seen,
the greater the mean absolute direction change, the
lesser the performance index is. Thus, it can be said,
that directional change supports anti-windup compen-
sation.
On the other hand, as in Tab. 1b, and Figs. 6, 7,
direction-preserving saturation does not cause direc-
tional change. Preserving a constant direction causes
performance indices to increase, dependless of the
method of anti-windup compensation. The coupling
is clearly visible during tracking when reference vec-
tor changes. Constant direction prevents the con-
troller from decoupling the plant – performance is in-
ferior.
In order to stipulate the differences in between
saturation methods, two GCT-AWC cases have been
chosen and compared with LMI-based approach.
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
50 100
0
0.5
−0.5
t
u
1,t
50 100
0
0.5
−0.5
t
u
2,t
50 100 150
0
10
−10
t
ϕ(v
t
) − ϕ(u
t
)
Figure 2: Overall performance for cut-off saturation with
GCT-AWC.
1516
5495
DB G CT MCT GCT
1655
0000
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
50 100
0
0.5
−0.5
t
u
1,t
50 100
0
0.5
−0.5
t
u
2,t
50 100 150
0
10
−10
t
ϕ(v
t
) − ϕ(u
t
)
Figure 3: Overall performance for direction-preserving sat-
uration with GCT-AWC.
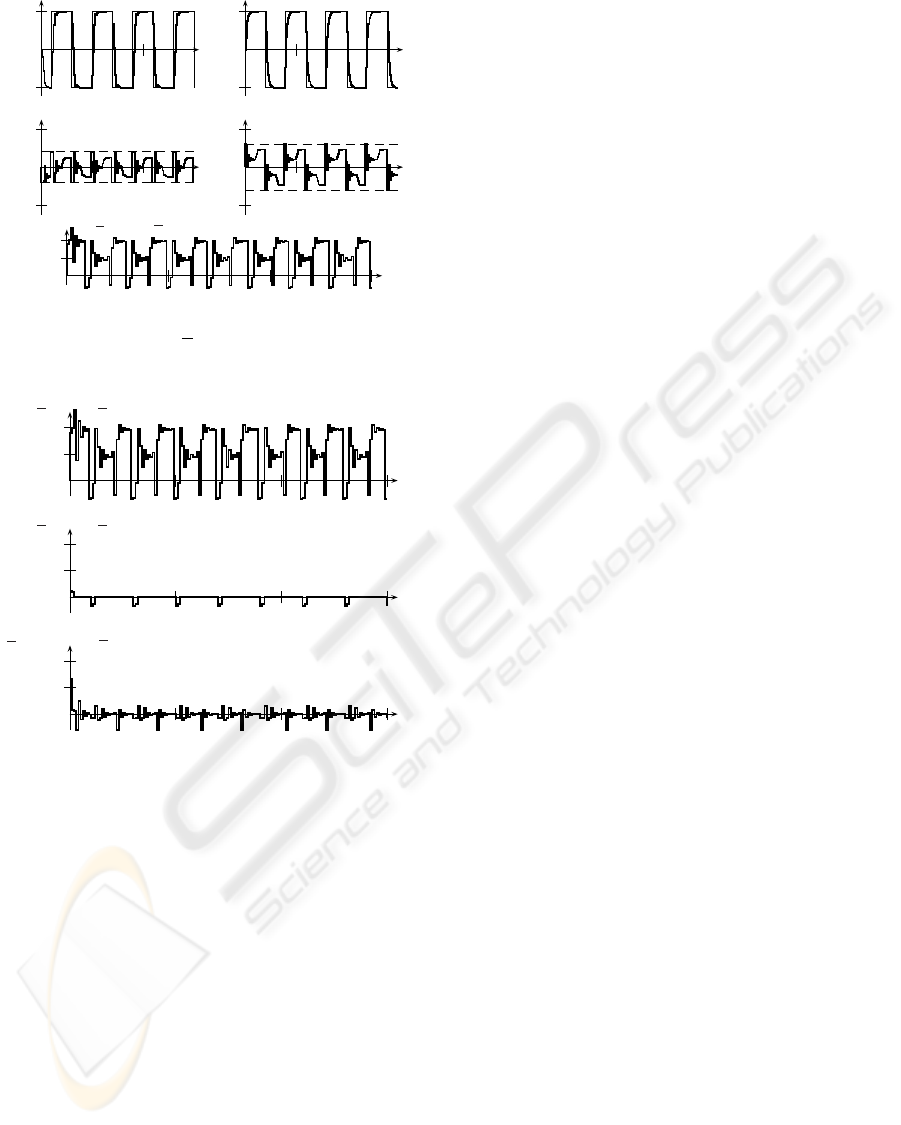
In the Fig. 8 one can see a priori anti-windup
compensator performance, where only feasible con-
trol actions are generated. The performance indices
in such a case are of the best values, i.e. J = 1.0450,
ϕ = 64.7063
◦
.
Having compared Figs. 2–8 it can be said, that in
order to achieve the best performance one has to al-
ter the direction of a computed control vector. The
greater the directional change is, the better the con-
trol performance.
For a priori AWC, visible changes in control di-
rection result from decoupling phase, i.e. whenever
control vector encounters constraints it has to be con-
strained in such a way as to achieve the high control
performance (the last plot corresponds to the angle
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
372

difference in between control vector computed in the
unconstrained case using optimisation algorithm, and
constrained a priori AWC control vector).
–
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
DB
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
G
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
CT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
MCT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
GCT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
Figure 4: Tracking performance for cut-off saturation.
–
50 100 150
0
10
−10
t
ϕ
t
DB
50 100 150
0
10
−10
t
ϕ
t
G
50 100 150
0
10
−10
t
ϕ
t
CT
50 100 150
0
10
−10
t
ϕ
t
MCT
50 100 150
0
10
−10
t
ϕ
t
GCT
50 100 150
0
10
−10
t
ϕ
t
Figure 5: Directional change for cut-off saturation.
On the other hand, having constrained the control
vector alters decoupling, thus its direction has to be
additionally altered, what is mostly visible in Fig. 8.
–
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
DB
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
G
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
CT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
MCT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
GCT
50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
Figure 6: Tracking performance for direction-preserving
saturation.
–
50 100 150
0
10
−10
t
ϕ
t
DB
50 100 150
0
10
−10
t
ϕ
t
G
50 100 150
0
10
−10
t
ϕ
t
CT
50 100 150
0
10
−10
t
ϕ
t
MCT
50 100 150
0
10
−10
t
ϕ
t
GCT
50 100 150
0
10
−10
t
ϕ
t
Figure 7: Directional change for direction-preserving satu-
ration.
Finally, in the Fig. 9 it has been shown that both
a priori and a posteriori AWCs need to alter direction
of controls in order to restore high quality of tracking
performance. In addition, a priori AWC has no fixed
structure, nor decoupling compensator, thus changes
DIRECTIONAL CHANGE AND WINDUP PHENOMENON
373

50 100
0
1
−1
t
y
1,t
50 100
0
1
−1
t
y
2,t
50 100
0
0.5
−0.5
t
u
1,t
50 100
0
0.5
−0.5
t
u
2,t
50 100 150
0
50
100
t
ϕ(v
t
) − ϕ(u
t
)
Figure 8: Overall performance for LMI-based control with
a priori AWC, J = 1.0450,
ϕ = 64.7063
◦
.
50 100 150
0
50
100
t
ϕ(v
t
) − ϕ(u
t
)
a)
50 100 150
0
50
100
t
ϕ(v
t
) − ϕ(u
t
)
b)
50 100 150
0
100
200
ϕ(v
GCT,t
) − ϕ(u
LMI,t
)
c)
t
Figure 9: A comparison of direction changes a) a priori
AWC, b) a posteriori GCT-AWC with cut-off saturation, c) a
priori AWC vs. GCT-AWC with cut-off saturation.
in control direction must be greater than in the case of
GCT-AWC with cut-off saturation.
The comparison of angle difference in between
unconstrained control vector computed for GCT case
and constrained control vector computed by a priori
AWC, shows that approximately a priori AWC acts in
the direction of unconstrained controller with GCT-
AWC, i.e. both of them try to get the system’s perfor-
mance as close as possible to the performance of ideal
pole-placement subject to no constraints.
Nevertheless, the simulations have shown that in
order to obtain a good performance one has to change
direction of control vector. Without the latter one will
observe coupling.
8 SUMMARY – NEW
DEFINITION OF WINDUP
PHENOMENON IN
MULTIVARIABLE SYSTEMS
One can formulate a new definition:
Solving the windup phenomenon problem does not
have to mean that constrained control vector is of the
same direction as computed control vector if cross-
coupling is present in the control system.
On the other hand, avoiding directional change in
control enables one to avoid windup phenomenon if
and only in the plant is perfectly decoupled or is not
coupled at all. (what due to the constraints is hardly
ever met)
Such a definition definitely changes the way one
should look at windup phenomenon and its connec-
tion with directional change problem.
REFERENCES
Horla, D. (2004). Direction alteration of control vector and
anti-windup compensation for multivariable systems
(in Polish). Studies in Automation and Information
Technology, 28/29:53–68.
Horla, D. (2006a). LMI-based multivariable adaptive pre-
dictive controller with anti-windup compensator. In
Proceedings of the 12th IEEE International Confer-
ence MMAR, pages 459–462, Miedzyzdroje.
Horla, D. (2006b). Standard vs. LMI approach to a con-
vex optimisation problem in multivariable predictive
control task with a priori anti-windup compensator. In
Proceedings of the 18th ICSS, pages 147–152, Coven-
try.
Peng, Y., Vran
ˇ
ci
´
c, D., Hanus, R., and Weller, S. (1998).
Anti-windup designs for multivariable controllers.
Automatica, 34(12):1559–1565.
Walgama, K. and Sternby, J. (1993). Contidioning tech-
nique for multiinput multioutput processes with input
saturation. IEE Proceedings-D, 140(4):231–241.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
374