
BINARY OPTIMIZATION: A RELATION BETWEEN THE
DEPTH OF A LOCAL MINIMUM AND THE PROBABILITY OF
ITS DETECTION
B. V. Kryzhanovsky, V. M. Kryzhanovsky and A. L. Mikaelian
Center of Optical Neural Technologies, SR Institute of System Analisys RAS
44/2 Vavilov Str, Moscow 119333, Russia
Keywords: Binary optimization, neural networks, local minimum.
Abstract: The standard method in optimization problems consists in a random search of the global minimum: a neuron
network relaxes in the nearest local minimum from some randomly chosen initial configuration. This
procedure is to be repeated many times in order to find as deep an energy minimum as possible. However
the question about the reasonable number of such random starts and whether the result of the search can be
treated as successful remains always open. In this paper by analyzing the generalized Hopfield model we
obtain expressions describing the relationship between the depth of a local minimum and the size of the
basin of attraction. Based on this, we present the probability of finding a local minimum as a function of the
depth of the minimum. Such a relation can be used in optimization applications: it allows one, basing on a
series of already found minima, to estimate the probability of finding a deeper minimum, and to decide in
favor of or against further running the program. The theory is in a good agreement with experimental
results.
1 INTRODUCTION
Usually a neural system of associative memory is
considered as a system performing a recognition or
retrieval task. However it can also be considered as a
system that solves an optimization problem: the
network is expected to find a configuration
minimizes an energy function (Hopfield,1982). This
property of a neural network can be used to solve
different NP-complete problems. A conventional
approach consists in finding such an architecture and
parameters of a neural network, at which the
objective function or cost function represents the
neural network energy. Successful application of
neural networks to the traveling salesman problem
(Hopfield and Tank, 1985) had initiated extensive
investigations of neural network approaches for the
graph bipartition problem (Fu and Anderson, 1986),
neural network optimization of the image processing
(Poggio and Girosi, 1990) and many other
applications. This subfield of the neural network
theory is developing rapidly at the moment (Smith,
1999), (Hartmann and Rieger, 2004), (Huajin Tang
et al, 2004), (Kwok and Smith, 2004), (Salcedo-
Sanz et al, 2004), (Wang et al, 2004, 2006).
The aforementioned investigations have the same
common feature: the overwhelming majority of
neural network optimization algorithms contain the
Hopfield model in their core, and the optimization
process is reduced to finding the global minimum of
some quadratic functional (the energy) constructed
on a given
NN
×
matrix in an N-dimensional
configuration space (Joya, 2002), (Kryzhanovsky et
al, 2005). The standard neural network approach to
such a problem consists in a random search of an
optimal solution. The procedure consists of two
stages. During the first stage the neural network is
initialized at random, and during the second stage
the neural network relaxes into one of the possible
stable states, i.e. it optimizes the energy value. Since
the sought result is unknown and the search is done
at random, the neural network is to be initialized
many times in order to find as deep an energy
minimum as possible. But the question about the
reasonable number of such random starts and
whether the result of the search can be regarded as
successful always remains open.
In this paper we have obtained expressions that
have demonstrated the relationship between the
depth of a local minimum of energy and the size of
5
V. Kryzhanovsky B., M. Kryzhanovsky V. and L. Mikaelian A. (2007).
BINARY OPTIMIZATION: A RELATION BETWEEN THE DEPTH OF A LOCAL MINIMUM AND THE PROBABILITY OF ITS DETECTION.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 5-10
Copyright
c
SciTePress

the basin of attraction (Kryzhanovsky et al, 2006).
Based on this expressions, we presented the
probability of finding a local minimum as a function
of the depth of the minimum. Such a relation can be
used in optimization applications: it allows one,
based on a series of already found minima, to
estimate the probability of finding a deeper
minimum, and to decide in favor of or against
further running of the program. Our expressions are
obtained from the analysis of generalized Hopfield
model, namely, of a neural network with Hebbian
matrix. They are however valid for any matrices,
because any kind of matrix can be represented as a
Hebbian one, constructed on arbitrary number of
patterns. A good agreement between our theory and
experiment is obtained.
2 DESCRIPTION OF THE
MODEL
Let us consider Hopfield model, i.e a system of N
Ising spins-neurons
1±=
i
s , Ni ,...,,21= . A state of
such a neural network can be characterized by a
configuration
)...,,,(
N
sss
21
=S . Here we consider
a generalized model, in which the connection
matrix:
∑
=
=
M
m
m
j
m
imij
ssrT
1
)()(
,
∑
=1
2
m
r
(1)
is constructed following Hebbian rule on M binary
N-dimensional patterns
)...,,,(
)()()( m
N
mm
m
sss
21
=S ,
Mm ,1=
. The diagonal matrix elements are equal to
zero (
0=
ii
T ). The generalization consists in the
fact, that each pattern
m
S is added to the matrix
ij
T
with its statistical weight
m
r . We normalize the
statistical weights to simplify the expressions
without loss of generality. Such a slight modification
of the model turns out to be essential, since in
contrast to the conventional model it allows one to
describe a neural network with a non-degenerate
spectrum of minima.
The energy of the neural network is given by the
expression:
∑
=
−=
N
ji
jiji
sTsE
1
2
1
,
(2)
and its (asynchronous) dynamics consist in the
following. Let
S be an initial state of the network.
Then the local field
ii
sEh ∂
−
∂= / , which acts on a
randomly chosen
i-th spin, can be calculated, and the
energy of the spin in this field
iii
hs−=
ε
can be
determined. If the direction of the spin coincides
with the direction of the local field (
0<
i
ε
), then its
state is stable, and in the subsequent moment (
1
+
t )
its state will undergo no changes. In the opposite
case ( 0>
i
ε
) the state of the spin is unstable and it
flips along the direction of the local field, so that
)()( tsts
ii
−
=
+
1 with the energy 01 <+ )(t
i
ε
. Such
a procedure is to be sequentially applied to all the
spins of the neural network. Each spin flip is
accompanied by a lowering of the neural network
energy. It means that after a finite number of steps
the network will relax to a stable state, which
corresponds to a local energy minimum.
3 BASIN OF ATTRACTION
Let us examine at which conditions the pattern
m
S
embeded in the matrix (1) will be a stable point, at
which the energy
E of the system reaches its (local)
minimum
m
E . In order to obtain correct estimates
we consider the asymptotic limit
∞→N . We
determine the basin of attraction of a pattern
m
S as
a set of the points of
N-dimensional space, from
which the neural network relaxes into the
configuration
m
S . Let us try to estimate the size of
this basin. Let the initial state of the network
S
be
located in a vicinity of the pattern
m
S . Then the
probability of the network convergation into the
point
m
S is given by the expression:
N
⎟
⎠
⎞
⎜
⎝
⎛
+
=
2
1
γ
erf
Pr
(3)
where
γ
erf is the error function of the variable
γ
:
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
N
n
r
Nr
m
m
2
1
12
2
)(
γ
(4)
and
n is Hemming distance between S
m
and S. The
expression (3) can be obtained with the help of the
methods of probability theory, repeating the well-
known calculation (Perez-Vincente, 1989) for
conventional Hopfield model.
It follows from (3) that the basin of attraction is
determined as the set of the points of the
configuration space close to
m
S , for which
m
nn
≤
:
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
6
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−=
2
0
2
0
1
1
1
2
rr
rr
N
n
m
m
m
(5)
where
NNr /ln2
0
=
(6)
Indeed, if
m
nn ≤ we have 1→Pr for
∞
→N ,
i.e. the probability of the convergence to the point
m
S asymptotically tends to 1. In the opposite case
(
m
nn > ) we have 0→Pr . It means that the
quantity
m
n can be considered as the radius of the
basin of attraction of the local minimum
m
E .
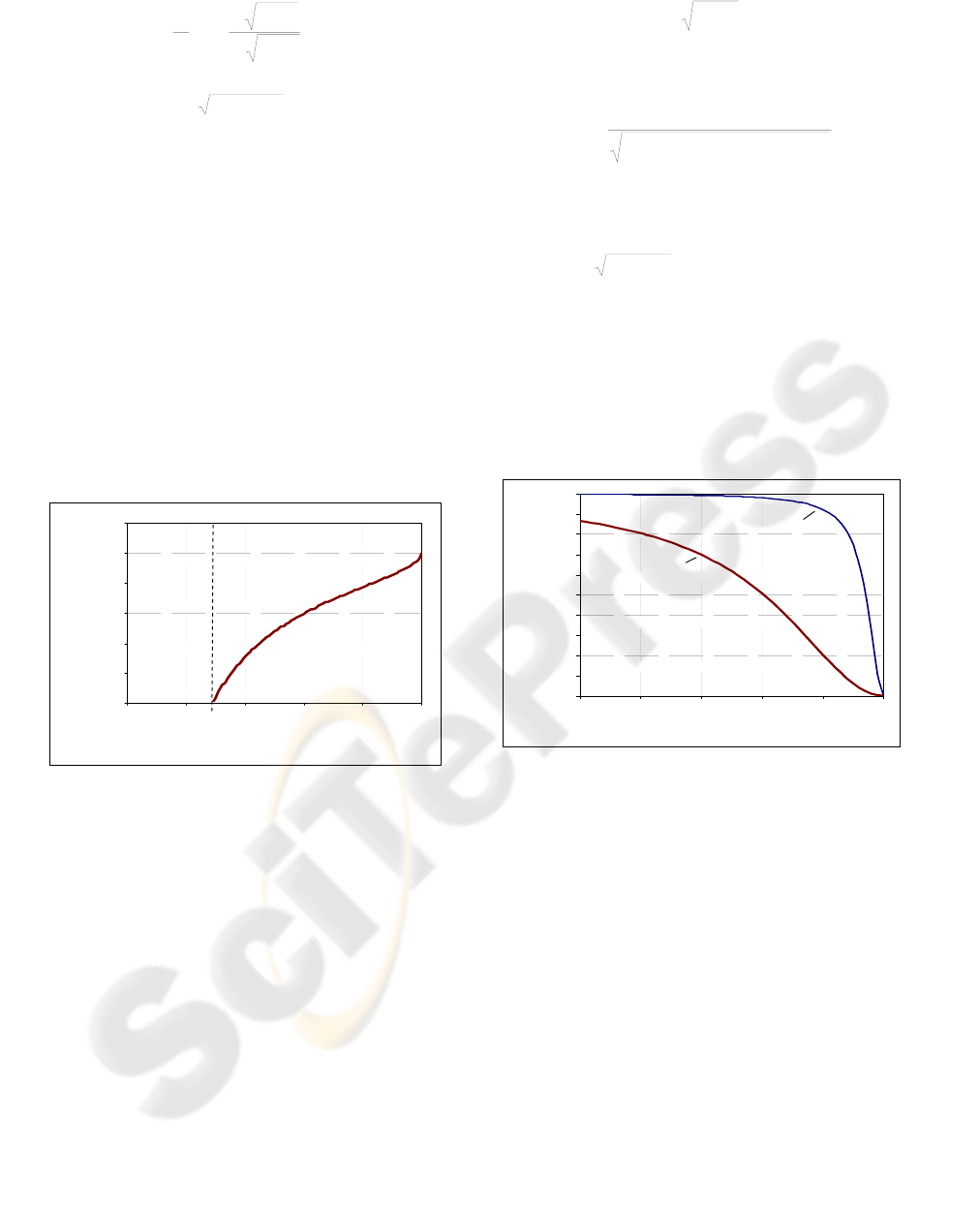
It follows from (5) that the radius of basin of
attraction tends to zero when
0
rr
m
→ (Fig.1). It
means that the patterns added to the matrix (1),
whose statistical weight is smaller than
0
r , simply
do not form local minima. Local minima exist only
in those points
m
S , whose statistical weight is
relatively large:
0
rr
m
> .
Figure 1: A typical dependence of the width of the basin
of attraction n
m
on the statistical weight of the pattern r
m
.
A local minimum exists only for those patterns, whose
statistical weight is greater than r
0
. For r
m
→r
0
the size of
the basin of attraction tends to zero, i.e. the patters whose
statistical weight
0
rr
m
≤ do not form local minima.
4 DEPTH OF LOCAL MINIMUM
From analysis of Eq. (2) it follows that the energy of
a local minimum E
m
can be represented in the form:
2
NrE
mm
−=
(7)
with the accuracy up to an insignificant fluctuation
of the order of
2
1
mm
rN −=
σ
(8)
Then, taking into account Eqs. (5) and (7), one can
easily obtain the following expression:
222
21
1
maxmin
min
/)/( EENn
EE
m
m
+−
=
(9)
where
NNNE ln
min
2−= ,
21
1
2
/
max
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∑
=
M
m
m
EE
(10)
which yield a relationship between the depth of the
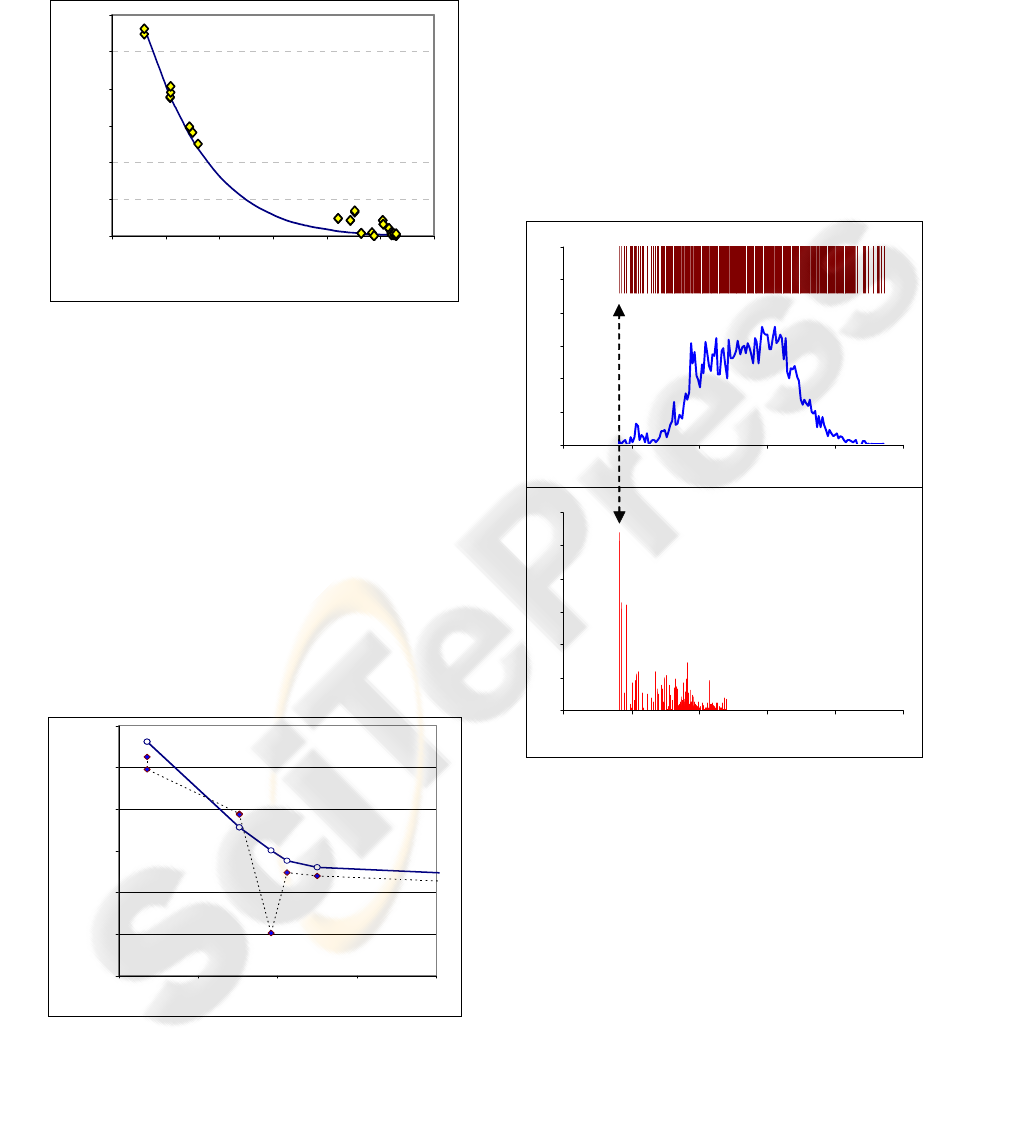
local minimum and the size of its basin of attraction.
One can see that the wider the basin of attraction, the
deeper the local minimum and vice versa: the deeper
the minimum, the wider its basin of attraction (see
Fig.2).
-1.0
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.0 0.1 0.2 0.3 0.4 0.5
n
m
/ N
E
m
/ N
2
a
b
Figure 2: The dependence of the energy of a local
minimum on the size of the basin of attraction: a) N=50;
b) N=5000.
We have introduced here also a constant E
max
,
which we make use of in what follows. It denotes
the maximal possible depth of a local minimum. In
the adopted normalization, there is no special need
to introduce this new notation, since it follows from
(7)-(9) that
2
NE −=
max
. However for other
normalizations some other dependencies of E
max
on
N are possible, which can lead to a
misunderstanding.
The quantity E
min
introduced in (10) characterizes
simultaneously two parameters of the neural
network. First, it determines the half-width of the
Lorentzian distribution (9). Second, it follows from
(9) that:
minmax
EEE
m
≤
≤
(11)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.0 0. 2 0.4 0.6 0.8 1.0
r
m
n
m
/ N
r
0
Nn
m
/
BINARY OPTIMIZATION: A RELATION BETWEEN THE DEPTH OF A LOCAL MINIMUM AND THE
PROBABILITY OF ITS DETECTION
7

i.e. E
min
is the upper boundary of the local
minimum spectrum and characterizes the minimal
possible depth of the local minimum. These results
are in a good agreement with the results of computer
experiments aimed to check whether there is a local
minimum at the point
S
m
or not. The results of one
of these experiments ( N=500, M=25) are shown in
Fig.3. One can see a good linear dependence of the
energy of the local minimum on the value of the
statistical weight of the pattern. Note that the
overwhelming number of the experimental points
corresponding to the local minima are situated in the
right lower quadrant, where
0
rr
m
> and E
m
< E
min
.
One can also see from Fig.3 that, in accordance with
(8), the dispersion of the energies of the minima
decreases with the increase of the statistical weight.
Figure 3: The dependence of the energy
m
E of a local
minimum on the statistical weight
m
r of the pattern.
5 THE PROBABILITY OF
FINDING THE MINIMUM
Let us find the probability W of finding a local
minimum
m
E at a random search. By definition, this
probability coincides with the probability for a
randomly chosen initial configuration to get to the
basin of attraction of the pattern
m
S . Consequently,
the quantity
)(
m
nWW = is the number of points in a
sphere of a radius
m
n , reduced to the total number
of the points in the
N -dimensional space:
∑
=
−
=
m
n
n
n
N
N
CW
1
2
(12)
Equations (5) and (12) define implicitly a
connection between the depth of the local minimum
and the probability of its finding. Applying
asymptotical Stirling expansion to the binomial
coefficients and passing from summation to
integration one can represent (12) as
Nh
eWW
−
=
0
(13)
where
h is generalized Shannon function
211 lnlnln +
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−+=
N
n
N
n
N
n
N
n
h
mmmm
(14)
Here
0
W is an insignificant for the further analysis
slow function of
m
E . It can be obtained from the
asymptotic estimate (13) under the condition
1>>
m
n , and the dependence )(
m
nWW = is
determined completely by the fast exponent.
It follows from (14) that the probability of finding
a local minimum of a small depth (
min
~ EE
m
) is
small and decreases as
N
W
−
2~ . The probability W
becomes visibly non-zero only for deep enough
minima
min
EE
m
>> , whose basin of attraction
sizes are comparable with
2/N . Taking into
account (9), the expression (14) can be transformed
in this case to a dependence
)(
m
EWW = given by
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=
22
2
0
11
max
min
exp
EE
NEWW
m
(15)
It follows from (14) that the probability to find a
minimum increases with the increase of its depth.
This dependence“the deeper minimum
→ the larger
the basin of attraction
→ the larger the probability to
get to this minimum” is confirmed by the results of
numerous experiments. In Fig.4 the solid line is
computed from Eq. (13), and the points correspond
to the experiment (Hebbian matrix with a small
loading parameter 10./
≤
NM ). One can see that a
good agreement is achieved first of all for the
deepest minima, which correspond to the patterns
m
S (the energy interval
2
490 NE
m
.−≤ in Fig.4).
The experimentally found minima of small depth
(the points in the region
2
440 NE
m
.−> ) are the so-
called “chimeras”. In standard Hopfield model
(
Mr
m
/1≡ ) they appear at relatively large loading
parameter
050./ >NM . In the more general case,
which we consider here, they can appear also earlier.
The reasons leading to their appearance are well
examined with the help of the methods of statistical
physics in (Amit et al, 1985), where it was shown
that the chimeras appear as a consequence of
-1. 0
-0. 5
0.0
0.0 0.2 0.4 0. 6 0.8
r
m
E
m
/ N
2
min
E
0
r
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
8
interference of the minima of
m
S . At a small
loading parameter the chimeras are separated from
the minima of
m
S by an energy gap clearly seen in
Fig.4.
0.00
0.02
0.04
0.06
0.08
0.10
0.12
-0.52 -0.50 -0.48 -0.46 -0.44 -0.42 -0.40
Minima depth
E
m
/ N
2
Probability
W
Figure 4: The dependence of the probability W to find a
local minimum on its depth
m
E : theory - solid line,
experiment – points.
6 DISCUSSION
Our analysis shows that the properties of the
generalized model are described by three parameters
r
0
, E
min
and E
max
. The first determines the minimal
value of the statistical weight at which the pattern
forms a local minimum. The second and third
parameters are accordingly the minimal and the
maximal depth of the local minima. It is important
that these parameters are independent from the
number of embeded patterns M .
Figure 5: The comparison of the predicted probabilities
(solid line) and the experimentally found values (points
connected with the dashed line).
Now we are able to formulate a heuristic approach
of finding the global minimum of the functional (2)
for any given matrix (not necessarily Hebbian one).
The idea is to use the expression (15) with unknown
parameters
0
W ,
min
E and
max
E . To do this one
starts the procedure of the random search and finds
some minima. Using the obtained data, one
determines typical values of
min
E and
max
E and the
fitting parameter
0
W for the given matrix.
Substituting these values into (15) one can estimate
the probability of finding an unknown deeper
minimum
m
E (if it exists) and decide in favor or
against (if the estimate is a pessimistic one) the
further running of the program.
0.0%
0.5%
1.0%
1.5%
2.0%
2.5%
3.0%
-0.65 -0.60 -0.55 -0.50 -0.45 -0.40
0.0%
0.5%
1.0%
1.5%
2.0%
2.5%
3.0%
-0.65 -0.60 -0.55 -0.50 -0.45 -0.40
a
b
Figure 6: The case of matrix with a quasi-continuous type
of spectrum. a) The upper part of the figure shows the
spectrum of minima distribution – each vertical line
corresponds to a particular minimum. The solid line
denotes the spectral density of minima (the number of
minima at length
E
Δ
). The Y-axis presents spectral
density and the X-axis is the normalized values of energy
minima
2
NE / . b) Probability of finding a minimum
with energy
E . The Y-axis is the probability of finding a
particular minimum (%) and the X-axis is the normalized
values of energy minima.
This approach was tested with Hebbian matrices at
relatively large values of the loading parameter
(
1020
÷
≥ ./ NM ). The result of one of the
experiments is shown in Fig.5. In this experiment
0.00
0.02
0.04
0.06
0.08
0.10
0.12
-0.66 -0.64 -0.62 -0.60 -0.58
Энергия минимума
Вероятность попадания в минимум
A
A
A
B
B
B
Probability W
2
NE
m
/
BINARY OPTIMIZATION: A RELATION BETWEEN THE DEPTH OF A LOCAL MINIMUM AND THE
PROBABILITY OF ITS DETECTION
9

with the aid of the found minima (the points
A ) the
parameters
0
W ,
min
E and
max
E were calculated,
and the dependence
)(
m
EWW
=
(solid line) was
found. After repeating the procedure of the random
search over and over again (
5
10~ random
starts)
other minima (points
B ) and the precise
probabilities of getting into them were found. One
can see that although some dispersion is present, the
predicted values in the order of magnitude are in a
good agreement with the precise probabilities.
In conclusion we stress once again that any given
matrix can be performed in the form of Hebbian
matrix (1) constructed on an arbitrary number of
patterns (for instance,
∞→M ) with arbitrary
statistical weights. It means that the dependence “the
deeper minimum
↔ the larger the basin of attraction
↔ the larger the probability to get to this minimum”
as well as all other results obtained in this paper are
valid for all kinds of matrices. To prove this
dependence, we have generated random matrices,
with uniformly distributed elements on [-1,1]
segment. The results of a local minima search on
one of such matrices are shown in Fig. 6. The value
of normalized energy is shown on the X-scale and
on the Y-scale the spectral density is noted. As we
can see, there are a lot of local minima, and most of
them concentrated in central part of spectrum (Fig
6.a). Despite of such a complex view of the
spectrum of minima, the deepest minimum is found
with maximum probability (Fig 6.b). The same
perfect accordance of the theory and the
experimental results are also obtained in the case of
random matrices, the elements of which are
subjected to the Gaussian distribution with a zero
mean.
The work supported by RFBR grant # 06-01-
00109.
REFERENCES
Amit, D.J., Gutfreund, H., Sompolinsky, H., 1985. Spin-
glass models of neural networks. Physical Review A,
v.32, pp.1007-1018.
Fu, Y., Anderson, P.W., 1986. Application of statistical
mechanics to NP-complete problems in combinatorial
optimization. Journal of Physics A. , v.19, pp.1605-
1620.
Hartmann, A.K., Rieger, H., 2004. New Optimization
Algorithms in Physics., Wiley-VCH, Berlin.
Hopfield, J.J. 1982. Neural Networks and physical
systems with emergent collective computational
abilities. Proc. Nat. Acad. Sci.USA. v.79, pp.2554-
2558 .
Hopfield, J.J., Tank, D.W., 1985. Neural computation of
decisions in optimization problems. Biological
Cybernetics, v.52, pp.141-152.
Huajin Tang; Tan, K.C.; Zhang Yi, 2004. A columnar
competitive model for solving combinatorial
optimization problems. IEEE Trans. Neural Networks
v.15, pp.1568 – 1574.
Joya, G., Atencia, M., Sandoval, F., 2002. Hopfield Neural
Networks for Optimization: Study of the Different
Dynamics. Neurocomputing, v.43, pp. 219-237.
Kryzhanovsky, B., Magomedov, B., 2005. Application of
domain neural network to optimization tasks. Proc. of
ICANN'2005. Warsaw. LNCS 3697, Part II, pp.397-
403.
Kryzhanovsky, B., Magomedov, B., Fonarev, A., 2006.
On the Probability of Finding Local Minima in
Optimization Problems. Proc. of International Joint
Conf. on Neural Networks IJCNN-2006 Vancouver,
pp.5882-5887.
Kwok, T., Smith, K.A., 2004. A noisy self-organizing
neural network with bifurcation dynamics for
combinatorial optimization. IEEE Trans. Neural
Networks v.15, pp.84 – 98.
Perez-Vincente, C.J., 1989. Finite capacity of sparce-
coding model. Europhys. Lett., v.10, pp.627-631.
Poggio, T., Girosi, F., 1990. Regularization algorithms for
learning that are equivalent to multilayer networks.
Science 247, pp.978-982.
Salcedo-Sanz, S.; Santiago-Mozos, R.; Bousono-Calzon,
C., 2004. A hybrid Hopfield network-simulated
annealing approach for frequency assignment in
satellite communications systems. IEEE Trans.
Systems, Man and Cybernetics, v. 34, 1108 – 1116
Smith, K.A. 1999. Neural Networks for Combinatorial
Optimization: A Review of More Than a Decade of
Research. INFORMS Journal on Computing v.11 (1),
pp.15-34.
Wang, L.P., Li, S., Tian F.Y, Fu, X.J., 2004. A noisy
chaotic neural network for solving combinatorial
optimization problems: Stochastic chaotic simulated
annealing. IEEE Trans. System, Man, Cybern, Part B -
Cybernetics v.34, pp. 2119-2125.
Wang, L.P., Shi, H., 2006: A gradual noisy chaotic neural
network for solving the broadcast scheduling problem
in packet radio networks. IEEE Trans. Neural
Networks, vol.17, pp.989 - 1000.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
10
